管状杆件应变片测量误差分析
吕凡任,邵红才,陈 丰,顾汉玉
(扬州市职业大学 土木工程学院,江苏 扬州 225009)
管状杆件应变片测量误差分析
吕凡任,邵红才,陈 丰,顾汉玉
(扬州市职业大学 土木工程学院,江苏 扬州 225009)
管状杆件受到剪力和弯矩作用,将产生应力和应变,通常采用应变片测量杆件的应变。应变片粘贴难以避免地将发生偏移和偏转,导致应变测量产生误差。基于应力状态和应力-应变弹性理论的分析,研究了直径为14~20 mm管状杆件不同位置的应力和应变及其误差,并分析了杆件泊松比对应变测量误差的影响。算例分析发现,应变片粘贴偏移不超过4 mm和偏转角度不超过4°导致的应变测量误差通常不超过5%。杆件的泊松比对于应变误差的影响基本可以忽略不计。
管状杆件;应变片;应变测量;误差分析;弹性理论
1 研究背景
岩土工程中桩基模型试验常常采用管状杆件用于模拟桩基础,分析弯矩和剪力作用下产生的应力大小、位移以及承载力情况[1-4]。管状杆件应变片粘贴位置难以避免地将产生或大或小的偏差,这个偏差对于应力测量产生怎样的影响是值得进行分析的。关于应变片粘贴位置偏差对于应变测量产生的影响情况,一些学者已经开展了一些研究:如田家熙[5]和刘明亮等[6]分析了梁或板的表面采用应变花测量应变时,应变片之间贴片的角度偏差引起的应变误差;栗震霄[7]根据应变片的测试原理和测试点的应力状态,分析应变片贴片位置误差对于应变测试结果的影响,发现当应变片的轴向与最大应变方向一致时,贴片位置偏差产生的应变测试误差较小;王永红[8]基于应变测量原理,分析了常见的柱式、环式及等截面梁式弹性元件应变测量时,应变片粘贴选择合理位置的重要性;周德泉等[9]为了提高水泥土搅拌桩、旋喷桩等低强度模型桩的应变测量质量,采用桩体表面开设凹槽的办法,凹槽内粘贴应变片,从而成功测量出桩身应变;李霞等[10]结合材料力学实验分析了矩形截面梁受到轴向拉力以及纯弯时,应变片粘贴位置偏差对于应变测量结果的影响情况。
上述这些研究,对应变片粘贴位置偏差可能产生的应变测试误差大小进行了分析,对于降低应变测量误差是有益的。但这些研究没有针对管状杆件应变片贴片误差等可能产生的应变测量误差的情况进行分析。
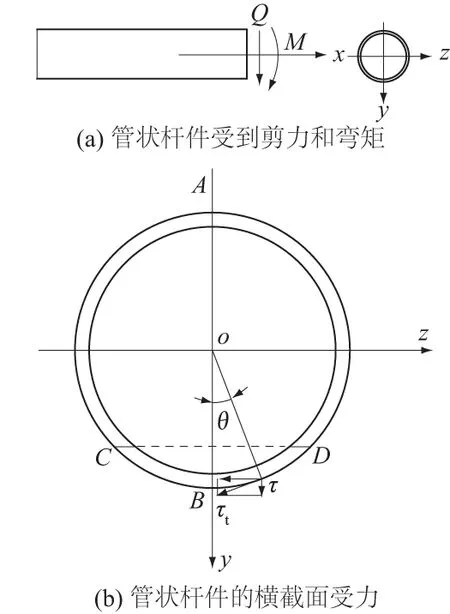
图1 管状杆件受力示意图Fig.1 Sketch of forces on tubular bar
本文将对管状杆件应变测量时,由于应变片粘贴位置的偏差,可能引起的应变测量误差以及误差大小的影响因素等进行分析。这些杆件通常处于弹性状态,应力-应变符合胡克定律。管状杆件的受力分析如图1(a)所示,杆件横截面受力分析如图1(b)所示。为了测量杆件的应变,通常将应变片粘贴在杆件外壁表面拉应变最大的地方,如图1(b)中的B点,并沿着杆件的轴向方向粘贴。但是,由于粘贴技术以及人工操作能力的局限,粘贴的应变片难以避免地将发生偏移量δ和偏转角α,如图2所示。
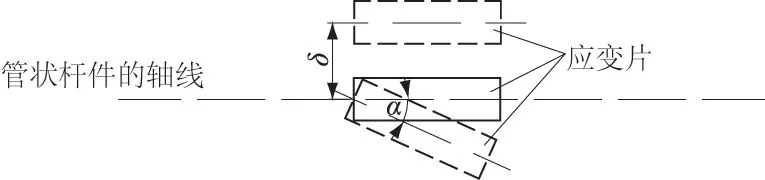
图2 应变片粘贴发生偏移或偏转
2 应力应变分析
分析如图1(a)所示的受到轴力和弯矩作用的管状杆件,在横截面上纵坐标为y的CD位置(见图1(b)),正应力和剪应力分别为:
(1)
(2)
式中:M,Q分别为杆件端部受到的弯矩和剪力;Iz为杆件横截面的惯性矩;b为分析点处的单元宽度。
其中,
(3)
式中:A为图1(b)中圆环在CD以下部分的面积;y1为圆环在CD以下部分微面积dA的y坐标。圆环内径为r,外径为R。对式(3)积分可得
(4)
式(2)中,
(5)
B点(图1(b))纵向(沿杆件轴向)的正应力可按式(6)计算,即
(6)
如果在B点有略微偏移,假设对杆件中心纵轴偏移的角度为θ(图1(b)),沿着纵向的正应力可按式(7)计算,即
(7)
由式(6)和式(7)可得
(8)
从式(8)可以看出,管的内径或者说壁厚的大小变化,对于应变片偏移时导致的应变测量误差没有影响。
横截面的外表面,y方向的剪应力为τ,沿着圆环外侧的切向剪应力为τt,如图1(b)所示,则切向剪应力可按式(9)计算,即
(9)
其中,
(10)
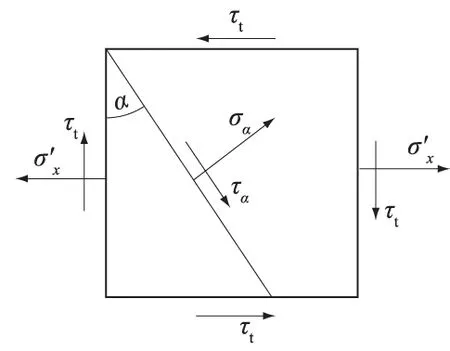
图3 应变片略有偏转处的应力Fig.3 Stresses at a slight deflection of strain gauge
B点略向右,纵向(沿杆件轴向)选取单元体,如图3所示,有一倾角为α的斜面上作用有正应力σα和剪应力τα(α略大于0°)。正应力σα和剪应力τα以及垂直于该截面上的正应力和剪应力分别按式(11)—式(14)计算。
(11)
(12)
(13)
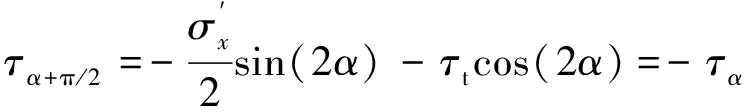
(14)
该斜面上的正应变和剪应变分别按式(15)和式(16)计算。
(15)
(16)
式中E,μ分别为杆件的弹性模量和泊松比。
3 算例分析
根据上述计算式,通过算例分析应变片粘贴位置发生偏差时,对于应变测量可能产生的影响。主要从应变片粘贴位置发生偏移和偏转2个方面进行分析,即应变片粘贴时发生沿着杆件轴线的只偏移、只偏转以及既有偏移又有偏转3种情况对于应变测试结果的影响(图2)。
杆件的泊松比μ=0.3,管状杆件的壁厚为1 mm时,随着应变片偏移量的增加,不同外径管状杆件应变误差的变化如图4所示。从图4可以看出,随着应变片偏移量的增加,应变误差逐渐增加,而且增加的幅度逐渐增大。表明降低应变片粘贴位置的偏移量,可以显著提高应变测量的准确性。同时还可以看出,当应变片偏移量不超过4 mm时,引起的应变误差总体上低于4%,这个误差值,土木工程中通常是可以接受的。从图4还可以看出,当管的外径增加时,由于应变片偏移而引起的应变误差逐渐降低,表明大直径的杆件更容易降低应变测量的误差。
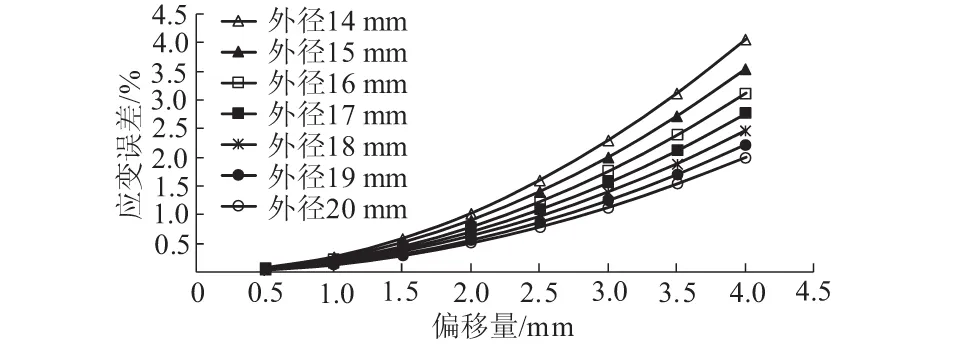
图4 壁厚1 mm、偏转角为0°时应变误差Fig.4 Strain errors when the wall thickness is 1 mm and the deflection angle is 0°
计算外径和应变片偏转发生的影响,得到表1。从表1发现,相同的壁厚、应变片相同的偏转角时,随着外径的增加,应变误差保持不变。
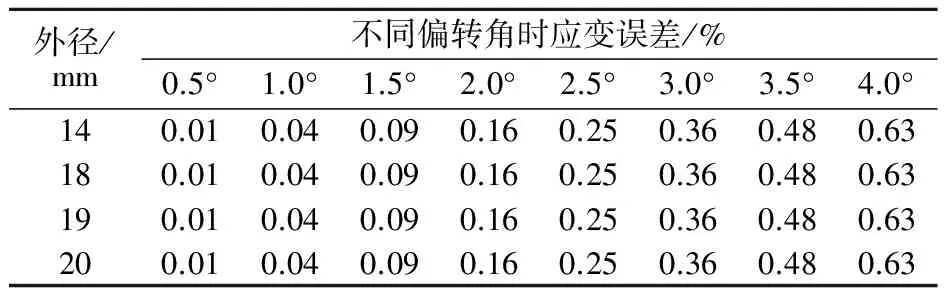
表1 壁厚1 mm、偏移量0 mm时应变误差
泊松比为0.3、外径为14 mm、壁厚1 mm时,随着应变片偏转角的增加,应变误差的变化如图5(a)所示;泊松比为0.3、外径为20 mm、壁厚1 mm时,随着应变片偏转角的增加,应变误差的变化如图5(b)所示。
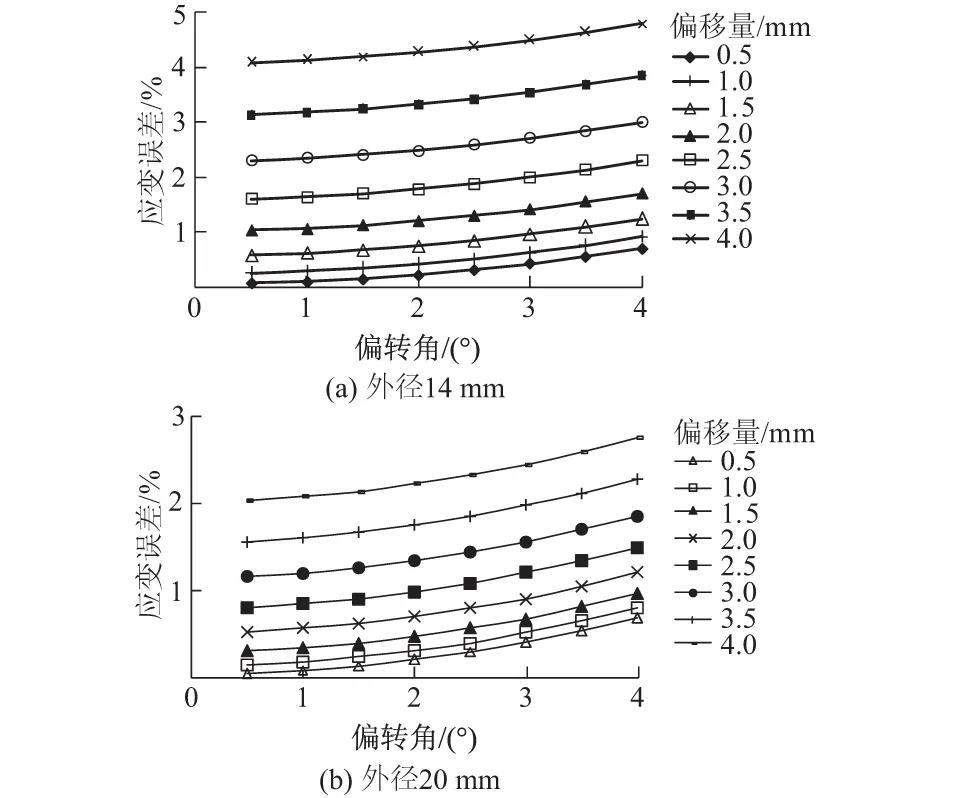
图5 壁厚1 mm时不同外径管状杆件应变误差Fig.5 Strain errors of tubular bar with different external diameters when the wall thickness is 1 mm
从图5(a)可以看出,随着应变片偏转角的增加,应变误差逐渐增加,并且增加的幅度逐渐增加。表明应变片偏转角的微小偏差,对于应变误差的影响比较小。但是,当应变片偏转角较大时,对于应变误差的影响是不容忽视的。从图5(a)可以看出,在应变片偏移量较大的情况下发生偏转,对应变误差的影响将更加显著。比较图5(a)和图5(b)可以发现,随着管外径的增加,应变片偏转角的增加导致的应变误差将降低。
管状杆件的外径为20 mm、壁厚1 mm、弹性模量为51.5 GPa、偏转角为0.5°情况下,当应变片的偏移量δ分别为1,2,3,4 mm时,随着泊松比μ的增加,应变误差的变化情况如图6所示。
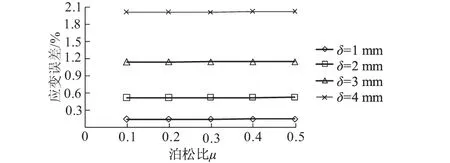
图6 外径R为20 mm、偏转角α为0.5°时泊松比和偏移量对应变误差的影响Fig.6 Effects of Poisson ratios and deviations on strain errors when the external diameter R is 20 mm and the deflection angle α is 0.5°
从图6可以看出,随着泊松比的增加,应变片不同的偏移量引起的应变误差略有增加。泊松比对于应变误差的影响很小,可以忽略不计。
管状杆件的外径为12 mm、壁厚为1 mm、应变片偏移量为2 mm、弹性模量为51.5 GPa情况下,当应变片偏转角α逐渐增加时,不同的泊松比引起的应变误差的变化情况如图7所示。
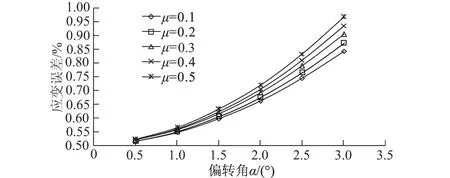
图7 外径R为20 mm、偏移量δ为2 mm时泊松比和偏转角对应变误差的影响Fig.7 Effects of Poisson ratios and deflection angles on strain errors when the external diameter R is 20 mm and the deviation δ is 2 mm
从图7可以看出:①随着应变片偏转角的增加,应变误差逐渐增加,并且,当泊松比增加的时候,这种增加的趋势更加显著;②不同泊松比的材料,当应变片偏转角在0°~3°变化时,应变误差不超过1%,一般的工程,这个误差都是可以接受的。综合图6和图7可以看出,泊松比对于应变误差的影响很小,基本可以忽略不计。
4 结论与展望
(1) 管状杆件的内径及壁厚大小对于应变片偏移或者偏转导致的应变误差是没有影响的。
(2) 随着应变片偏移量的增加,应变误差逐渐增加。但对于外径为14~20 mm的管状杆件,当应变片的偏移量不超过4 mm时,应变误差不超过5%。管状杆件的外径较小时,应变片的偏移量对应变的误差影响更大。
(3) 随着应变片偏转角度的增加,应变误差逐渐增加,并且在应变片偏移的同时还发生偏转,应变误差更大。但是,对于应变片偏移量为4 mm时还发生4°的偏转,应变误差不超过5%。当管状杆件的外径增加时,应变片的偏移和偏转对于应变误差的影响将降低。
(4) 管状杆件的泊松比对应变片偏移和偏转导致的应变误差影响很小,基本可以忽略不计。
本文研究是基于管状杆件采用应变片测量应变的理论分析,今后还需要考虑实际试验中应变片标距对于应变测量误差的影响。
[1] 吕凡任,邵红才,金耀华. 对称双斜桩基础水平承载力模型试验研究[J]. 长江科学院院报,2013, 30(2): 67-70.
[2] 邵红才,吕凡任,金耀华,等. 竖向荷载作用下对称双斜桩基础水平承载力模型试验研究[J]. 长江科学院院报,2014,31(6):65-68.
[3] 江 浩,汪 稔,吕颖慧,等. 钙质砂中模型桩的试验研究[J]. 岩土力学,2010, 31(3):780-784.
[4] 曹卫平,陆清元,樊文甫. 竖向荷载作用下斜桩荷载传递性状试验研究[J]. 岩土力学, 2016,37(11):3048-3056.
[5] 田家熙. 应变花角度偏差对主应变测量的影响及其消除方法[J]. 武汉钢铁学院学报, 1984,(3):31-36.
[6] 刘明亮, 高文华. 应变花贴片偏位误差的分析[J]. 佳木斯工学院学报,1996,14(1):62-65.
[7] 栗震霄. 应变片的贴片方位偏差对测量结果的影响[J]. 计量技术,1994,(9):23-25.
[8] 王永红. 电阻应变片粘贴位置对测量结果的影响[J]. 硫磷设计,1997,(1):31-35.
[9] 周德泉, 陈 坤, 赵明华,等. 室内模型实验中低强度桩侧应变片粘贴技术与应用[J]. 实验力学,2009,24(6):558-562.
[10]李 霞, 周克民. 材料力学基本实验中应变片粘贴误差分析[J]. 大学物理实验,2010,23(6):83-85.
(编辑:罗 娟)
Strain Error of Strain Gauge on Tubular Bar
LÜ Fan-ren, SHAO Hong-cai, CHEN Feng,GU Han-yu
(Civil Engineering Department, Yangzhou Polytechnic College, Yangzhou 225009, China)
Tubular bar will produce stress and strain when bearing shear force and bending moment. Strain of bar is usually measured by strain gauge. Strain gauge will deviate and deflect inevitably when pasted to the tubular bar, resulting in strain measurement errors. According to stress state and elastic theory of stress-strain, the stress, strain and their errors at different positions of tubular bars with diameters of 14-20 mm were analyzed. Example analysis indicates that the strain error is not more than 5% when the deviation is not more than 4 mm and the deflection is not more than 4°. The influence of Poisson ratios of tubular bar on strain error can be basically neglected.
tubular bar; strain gauge; strain measurement; error analysis; elastic theory
2016-04-06;
2016-05-10
江苏省第四期“333”工程培养对象资助项目;江苏省高等学校大学生创新创业训练计划项目(201511462013X)
吕凡任(1970-),男,安徽寿县人,教授,博士,主要从事地基基础方面的教学和研究工作,(电话)0514-87697118(电子信箱)frlv88@qq.com。
10.11988/ckyyb.20160318
2017,34(7):140-143
TU473.1;O348.2
A
1001-5485(2017)07-0140-04

