一种改进的空间相关系数在水库高边坡外观变形监测中的应用
胡添翼, 游梦陶, 陆天琳, 王 成, 董安雨
(1.河海大学 水利水电学院, 南京 210098; 2.上海市政工程设计研究总院 水利水运设计研究院,上海 200092; 3. 上海市水务建设工程安全质量监督中心站,上海 200070)
一种改进的空间相关系数在水库高边坡外观变形监测中的应用
胡添翼1,2, 游梦陶2, 陆天琳3, 王 成1, 董安雨1
(1.河海大学 水利水电学院, 南京 210098; 2.上海市政工程设计研究总院 水利水运设计研究院,上海 200092; 3. 上海市水务建设工程安全质量监督中心站,上海 200070)
水库大坝常涉及边坡工程,传统边坡监测主要针对单个测点的变形和应力的变化情况,不太注重多测点边坡整体变形状态的分析。基于Pearson相关系数和Moran相关系数,考虑不同测点的空间坐标,提出一种空间相关系数,用以分析边坡各测点空间上的关联性质;并建立边坡外观变形监测的3个关联性指标:测点关联度Rij、测点影响度Ii、边坡整体度I。通过指标的变化趋势,从关联性角度实现对边坡整体性质的把握。通过对某混凝土坝左岸高边坡外观变形资料的分析,本文提出的空间相关系数符合实际,3个关联性指标具有一定的合理性,对分析边坡安全状态有一定辅助作用。
高边坡;外观变形监测;Pearson相关系数;Moran相关系数;空间相关系数
1 研究背景
库岸边坡是一种常见涉水工程,其稳定状态与工程安全息息相关。历史上关于边坡灾害有很多案例,如1963年意大利瓦依昂水库滑坡致使约1 900人死亡,700人受伤[1];1985年长江上游新滩滑坡涌浪波及上下游江段42 km,古镇新滩全部被毁;2007年湖北省巴东县约500万m3滑坡体坠入清江,造成8人失踪。滑坡已位列3大全球性地质灾害[2-3]。随着经济发展和技术进步,大坝高度也与日俱增,水库高边坡安全监测意义重大。
就理论角度而言,边坡稳定性分析主要有极限平衡法[4]、数值分析法[5]等确定性方法和时间序列分析法[6]、模糊数学法[7]、神经网络算法[8]等不确定性方法。近年来,有一些新的分析方法涌现,如杜岩等[9]基于GIS三维滑坡分析模块,将坡体重点测点的黏聚力作为动态参量,实现对边坡体的动态稳定分析评价;李南生等[10]考虑包括中间主应力的坝体各应力分量对土质材料强度的影响,在土石坝边坡稳定分析中采用非线性统一强度理论;王海军等[11]运用一种基于果蝇优化算法的广义回归神经网络模型预测边坡稳定状态,取得了比较理想的预测效果。但是这些研究方法着重考虑单个测点的安全状况,没有考虑测点之间的相互作用。
就工程角度而言,目前已有很多工程手段被用来监测边坡安全状态,比如对边坡进行外部变形监测,采用多点变形计、钻孔斜侧移和铟钢丝变形计等仪器对边坡进行内部应力变形监测等。因为高边坡本身具有复杂性,多变的地质条件,辅以严酷的自然环境,使得监测仪器经常出现不同程度的损坏;如果同时考虑监测数据中可能存在的误差等数据异常问题,能够被有效利用的监测数据十分有限。利用相对有限的监测数据,对边坡安全状态进行有效的数据挖掘[12],成为边坡安全监测领域的新热点。
本文基于Pearson积矩相关系数(Pearson correlation coefficient)和Moran空间自相关系数(Moran’sI),考虑这2种系数的优缺点,结合边坡测点的空间坐标,提出一种新的空间相关系数。将这种空间相关系数引入边坡安全性分析,从不同测点变形测值的关联性这一角度来分析边坡的整体性,并针对边坡测点安全监测提出了测点关联度、测点影响度和边坡整体度3个关联性指标,从关联性的角度为边坡变形监测提供辅助信息。
2 几种相关系数
2.1 Pearson积矩相关系数
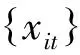
(1)
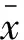
Pearson相关系数取值范围为[-1,1],系数为正表示线性正相关,系数为负表示线性负相关,一般通过相关系数绝对值的取值范围来判断变量之间相关强度的大小。
2.2Moran空间自相关系数
Moran空间自相关系数可以衡量某一时刻空间上邻近位置是否有相似取值。该系数取值范围为[-1,1],正数表示高数值与高数值(或低数值与低数值)相邻,负数表示高数值与低数值相邻。假设边坡有m个监测点,任意截面全局Moran自相关系数公式为
(2)
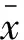
(3)
根据Cliff和Ord(1981)和Goodchild(1986)的推导,在正态假设条件下,Moran’sI的期望值EN(I)和方差VarN(I)分别为:
(4)
(5)
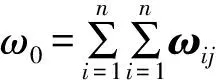
3 一种考虑空间距离的空间相关系数
3.1 Pearson相关系数和Moran空间自相关系数的不足
Pearson相关系数可以计算2个测点数据的线性相关程度,其基于一定时间内2个序列的历史值,计算的是序列的相关性大小,但是不能计算3个或者3个以上序列的相关性;该系数也不能反映2个监测点之间的物理距离。
Moran空间自相关系数可以考察空间上截面数据的分布(聚集)情况,但是没有考虑序列的历史值,难以反映测值序列之间的相互影响;根据Tobler地理学第一定律[13-15]:“任何事物都相关,只是相近的事物关联更紧密”,Moran所定义的ωij权重矩阵仅仅考虑基于邻近标准的相邻测点的数值变化,没有考虑非临近测点的变化和测点的空间距离[16-18]。
3.2 一种改进的空间相关系数
针对前文2种相关系数的不足,尝试提出一种改进的空间相关系数。
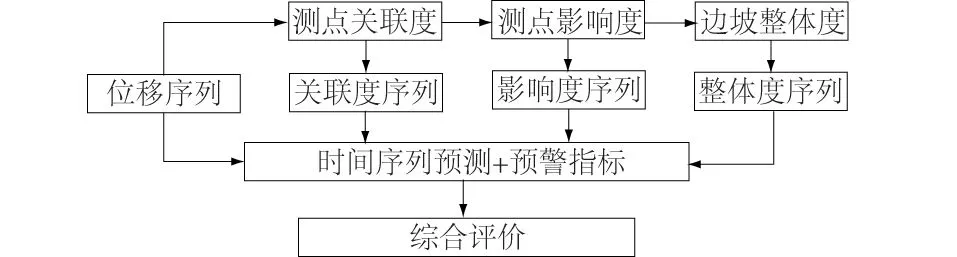
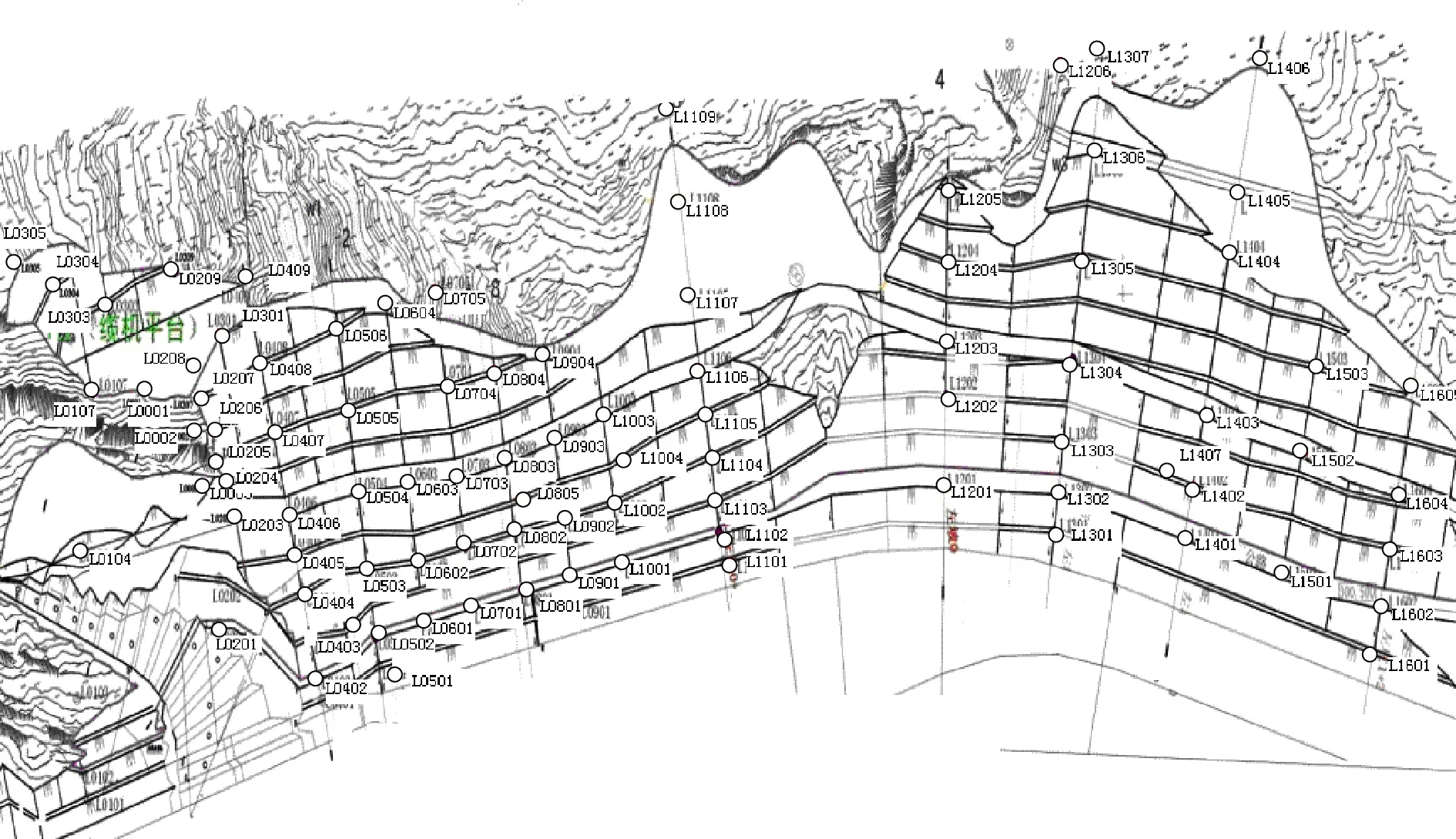
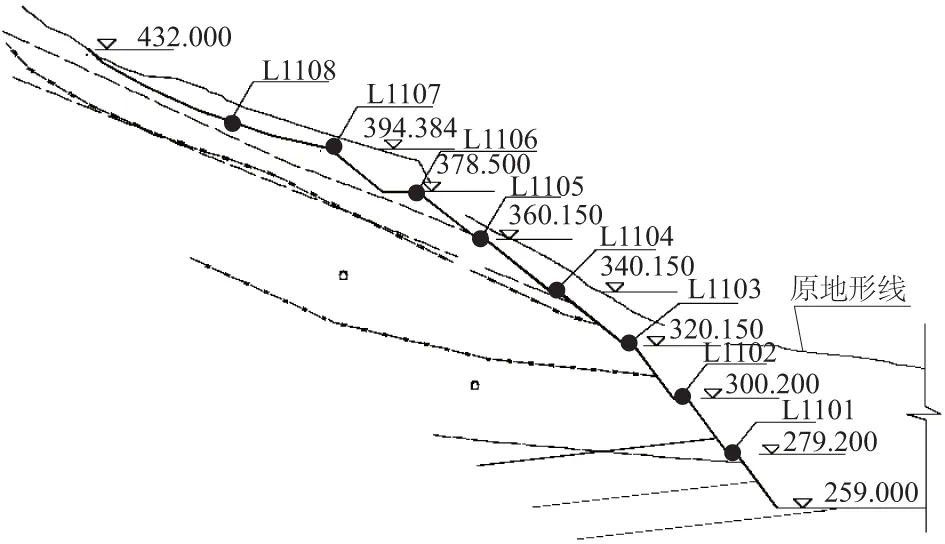
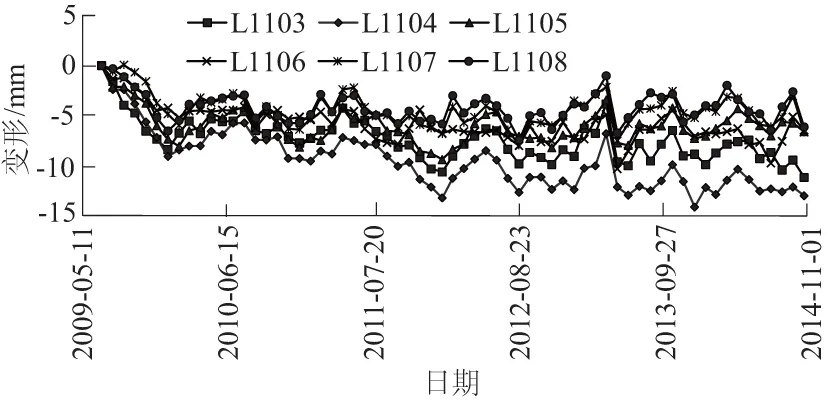
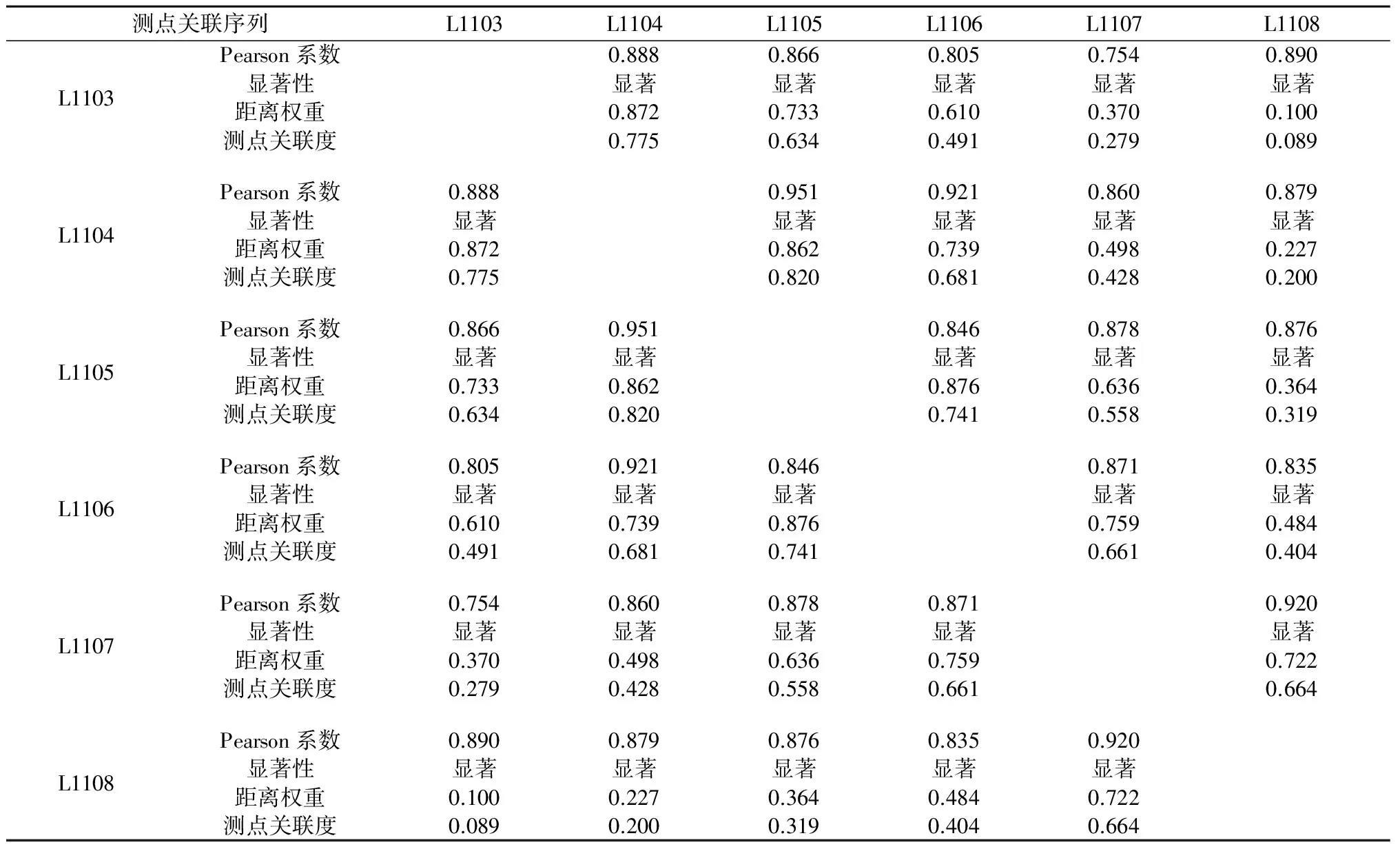
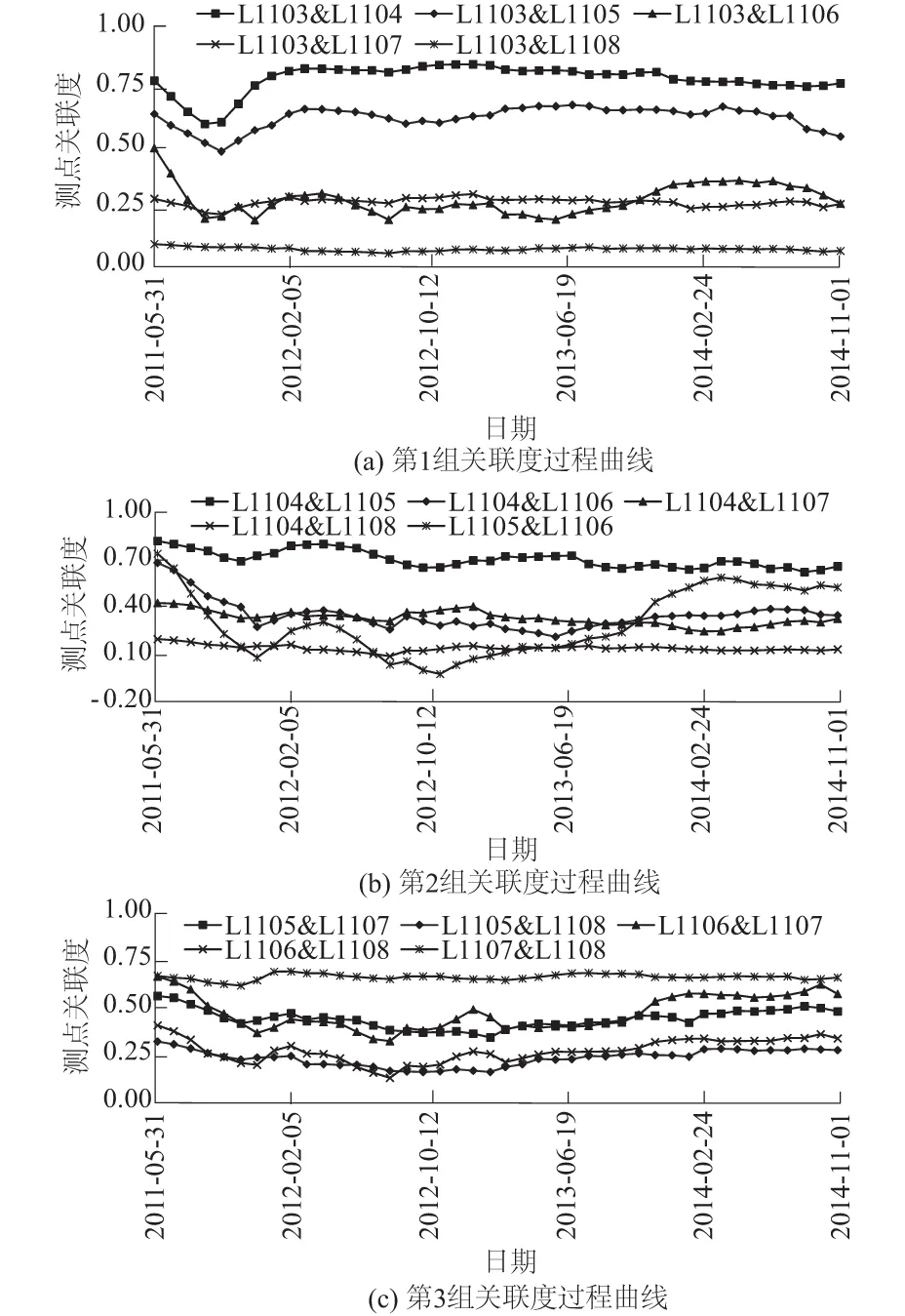
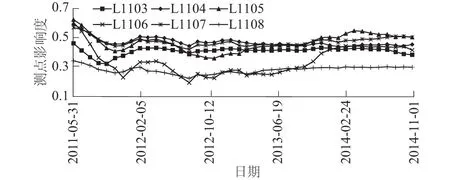
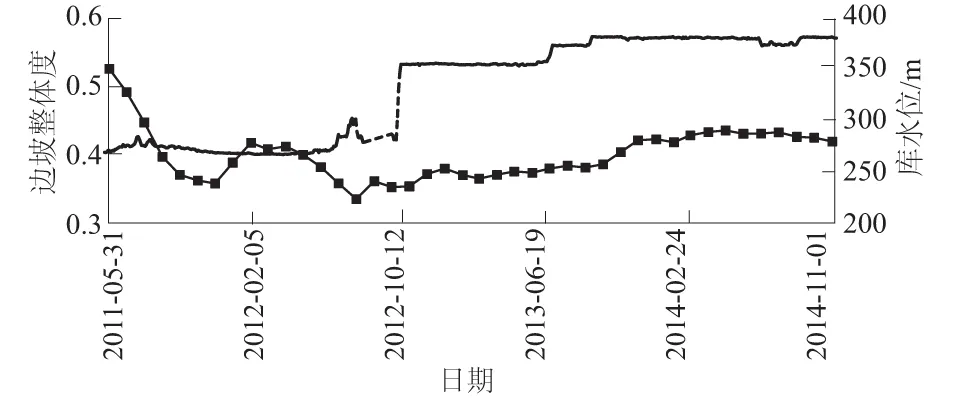
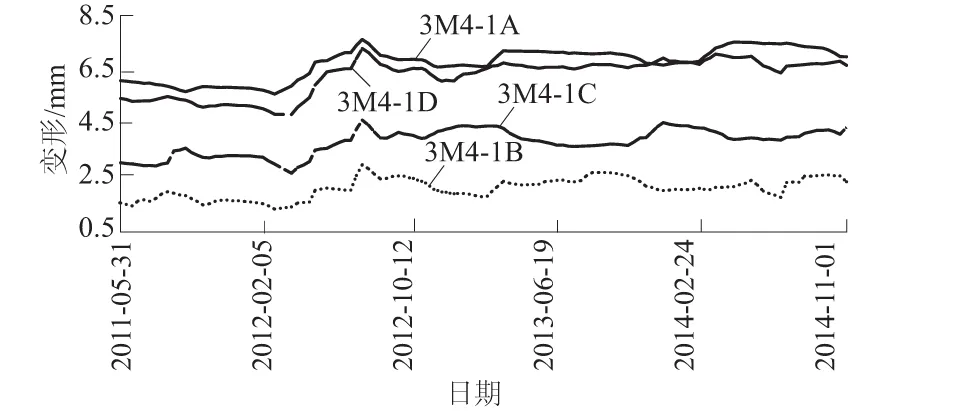
假设在一个三维空间有A,B,C,D 4个测点,且这4个测点空间位置不尽相同,具体分布情况如图1所示。时间T为纵轴坐标,测点的变形值随时间不断变化。不失一般地假设A测点和B测点之间距离较近,C测点和D测点之间距离较远;同时假设A测点和C测点数据完全相同,B测点和D测点数据完全相同。A和B两测点距离记为S1;C,D之间距离记为S2,显然有S1 图1 A,B,C,D的空间数据模型Fig.1 Spatial data model of A, B, C, D 基于以上假设,定义空间距离权重矩阵ωij′为 (6) 对于三维坐标,有 (7) (8) 因为系数Rij考虑了测点的空间位置,称这种相关系数为“空间相关系数”。进一步,假设全局有m个测点,针对测点i,可以计算出测点i和除测点i本身以外m-1个测点的相关系数,并计算这些相关系数的平均值。这里称该值为测点i的局部相关系数Ii,其公式为 (9) 求全局所有测点的局部相关系数,并对局部相关系数求均值,可得到全局相关系数I,即 (10) 4.1 3个关联性指标 边坡系统是一种多层次、非线性复杂系统,工程上一般用监测点的变形数值反映边坡对应区域的变形性态。边坡不同测点(区域)监测值之间有一定的关联性质,这种关联性质会随着时间和环境的变化慢慢转移;一些测点(区域)的变形可能会对周围测点(区域)造成一定影响;另外,边坡变形的整体性随时间也是变化的。利用前文提出的空间相关系数及其引申系数,针对边坡变形监测提出3个关联性指标,具体如图2所示。 图2 关联性指标Fig.2 Relevance indexes 4.1.1 测点关联度 测点关联度表示2个测点变形相关程度的大小,用Rij表示。取边坡上任意2个测点a和b,各取相同时间段内的时间序列,计算这2个测点变形序列的空间相关系数,作为测点a和测点b变形的测点关联度Rij。如果2个测点的关联度很高,则说明这2点之间的岩体整体性较好,一旦其中一个测点发生较大变形,另一个测点很有可能也产生比较大的变形。 4.1.2 测点影响度 测点影响度表示边坡任意一个测点i的变形对边坡整体变形的影响程度,用Ii表示。计算某一个测点和整个边坡其他所有测点的关联程度,然后对这些关联性求平均数,得到的数值称为该点的影响度Ii。根据边坡所有测点影响度的大小,可以对测点进行排序,得到影响度较大的测点,作为边坡安全的关键点。 4.1.3 边坡整体度 边坡整体度表示整个边坡测点的整体性的大小,用I表示。如果已经得到了所有测点的影响度Ii,对这些测点的影响度进行求和平均,就得到了边坡的整体度I。需要注意的是,边坡整体度仅仅表征边坡的整体性,而整体度本身不能直接反映边坡的安全性。如果边坡的整体度高,此时某些部位一旦出现较大变形,更有可能造成整体性的滑动破坏;如果边坡的整体度低,则说明边坡各部分位移相对独立,如果边坡发生破坏的话将以局部破坏为主。 4.1.4 3个关联性指标与变形的关系 得到以上3个关联性指标,结合边坡各个测点的实测变形数值,我们可以大概判断边坡的破坏形式,评价边坡安全状态。为表达方便,关联性、变形和边坡的破坏形式三者的关系可以用象限图的形式来表示,具体如图3所示。 图3 关联指标和变形大小关系 4.2 基于空间相关系数的边坡关联性评价体系 从边坡测点的变形序列,可以得到基于空间相关系数的边坡关联性Rij,Ii,I指标,这些指标因为时间不同,其数值也是动态变化的。进一步,可以得到3个指标的时间序列,从而对3个指标进行一定的分析和预测,结合单个测点变形状况,判断整个剖面的变形趋势和关键测点的转移趋势;另一方面,利用已有监测数据作为样本,可以建立这3个指标的预警指标,针对可能出现的危险情况提前采取相应措施。结合了空间相关系数的评价体系如图4所示。 图4 空间相关系数评价体系Fig.4 Evaluation system of spatial relevance indexes 5.1 工程背景 某混凝土坝电站位于四川省与云南省交界处金沙江下游河段,为满足二期工程布置需要,下游左岸开挖形成长约1 530 m,最大坡高约230 m的人工高边坡。因高边坡稳定性将直接影响二期工程安全,需进行安全监测。高边坡内观变形监测采用多点变形计共160套,截至2014年底仪器失效较多,内观变形监测受到较大影响;外观变形监测数据相对完整,有较高参考价值。外观变形监测设有16个监测剖面,布置94个变形测点,实际观测点81个,主要为水平和垂直变形共用点。其中,L03—L05及L11—L13为重点剖面,大致每月观测1次。测点布置如图5。 图5 某混凝土坝左岸高边坡测点平面布置Fig.5 Layout of measuring points at left bank high slope of a concrete dam 其中重点剖面L11上测点L1101,L1102,L1109因为施工等原因已经失效,不能继续观测;有效测点L1103—L1108大致均匀分布在320~431m高程范围内,以这部分测点所在测点作为实例研究,布置如图6所示。考虑文章篇幅,现仅以L11剖面上有效测点从2009年7月1日至2014年11月1日沿左右岸方向单个方向的变形序列(符号以向左岸方向为正,向河床方向为负)共65个截面数据为例进行研究。断面变形情况如图7所示。 图6 左岸L11剖面测点布置Fig.6 Layout of measuring points on profile L11 of left bank 图7 左岸L11剖面测点沿左右岸方向变形过程线Fig.7 Process lines of displacement of measuring points on profile L11 towards lefts bank and right bank 5.2 空间相关系数 5.2.1 测点关联度 首先根据各个测点的坐标计算不同测点之间的空间距离,根据式(6)计算各个测点之间的距离权重系数;然后每次取时间k之前(包括k时刻)24个变形数据,计算结果作为k时刻的空间相关系数;最后计算时间点k+1,k+2,k+3,…,以此类推,便可以得到关于时间的测点关联度序列。对于L11剖面而言,2011年6月1日的关联性为序列的第1个测值。具体关联度如表1所示。 表1 L11剖面测点关联度计算结果(2011年6月1日) 图8 左岸L11剖面测点关联度变化过程线Fig.8 Time-history curves of relevance degree of measuring points on profile L11 of left bank 从表1可知,整体上距离近的测点之间的测点关联度明显要比距离远的测点之间的测点关联度要大一些,这也充分体现了距离权重的作用;测点L1104和测点L1105的测点关联度最强,为0.820;测点L1103和测点L1108的测点关联度最弱,为0.089;从相邻测点的测点关联度来看,位于剖面上部和下部的测点关联度较高,位于中部的L1105和L1106的关联度较低,表明中部测点附近变形的独立性更强,更易发生局部破坏。 进一步建立剖面测点关联度时间序列,一共有15条关联度过程线,如图8所示。图8中大部分测点之间的关联性质比较稳定的,但是L1105和L1106的测点关联度出现了比较明显的波动情况,并且在2013年底出现了明显的上升,推测和2013年底水库蓄水有一定关系,需要持续关注。可以看出,不同测点之间的测点关联度并不是一成不变的,而是随着边坡周围环境和时间的推移不断变化的,这也体现了建立关联度时间序列的必要性。 5.2.2 测点影响度 测点影响度表示单个测点的变形对边坡整体的影响程度,L11断面测点影响度变化过程线如图9所示。 图9 左岸L11剖面测点影响度变化过程线Fig.9 Time-history curves of the influence degree of measuring points on profile L11 of left bank 从图9中可以看出,到2014年11月1日,影响度最低的测点为L1108,较高的测点为L1105;大部分测点的影响度变化都比较平稳,表明测点和其他点的关联性质是比较稳定的,但L1105和L1106出现较大波动,需重点关注。 表2 各测点影响度预测值与实测值对比 表3 各测点变形预测与实测值对比 5.2.3 边坡整体度 边坡整体度反映边坡变形的整体性,L11剖面边坡整体度变化过程如图10所示。 从整个剖面来看,边坡整体度在初始阶段较高,但随时间推移,边坡整体度总体呈现波动下降的趋势,说明剖面各个测点的变形变得更加独立,出现整体滑坡的风险越来越小;2012年和2013年水库分别进行了2次蓄水,边坡整体度有了一定上升,但上升幅度较小,整体度变化趋势仍需重点关注。 图10 左岸L11剖面边坡整体度变化过程线Fig.10 Time-history curves of slope’s integrity degree of profile L11 of left bank 5.3 整体评价 有了关联性指标序列和测点变形序列,可以运用统计学方法对这些序列进行预测,判断边坡的变化趋势。具体的,采用ARIMA模型对各个测点的影响度和测点的变形进行预测,所有测点的预测结果和对应实测值如表2和表3所示。 从测点影响度的预测结果来看,L1103和L1104测点影响度表现出缓慢上升的趋势,L1105—L1108测点影响度则缓慢下降,L1107的影响度是所有测点里最高的;整体而言,边坡整体度出现了缓慢下降的趋势。从测点变形的预测结果来看,所有测点的变形都有进一步向河床方向变形的趋势,但变形量较小。进一步,将预测值和实测值进行比对可以发现,虽然实测值的数据波动更大,但是预测值还是比较好地反映了数值的变化趋势。 事实上,L11断面设有4M4-1(341.150 m)和4M4-2(301.200 m)2支多点位移计,以观察断面内部岩体的变形状况;截至2014年11月1日,两支多点位移计都出现了损坏,已不能正常使用。为了解边坡内部岩体的变形情况,选取断面附近数据较完整的3M4-1多点位移计(385.00 m)进行研究,其位移情况如图11所示。从图11中可以看出,L11断面附近区域内部岩体变形稳定;不同深度岩体变形表现出一定的一致性和相关性,边坡整体性好且整体性较为稳定。该结论和前文分析和预测的结果相符,说明本文提出的空间相关系数有一定实际价值。 图11 3M4-1多点位移计变化过程线Fig.11 Time-history curves of deformation at 3M4-1 multi-point extensometer 综上,可以认为左岸边坡L11断面变形稳定,发生大面积滑动破坏的可能性较小,需重点防范局部破坏的发生(尤其是中部位置);另外,测点L1105和L1106的关联度和影响度都出现了较大波动,需要持续关注。 本文在Pearson积距相关系数和Moran空间自相关系数的基础上,考虑不同测点的空间坐标,提出了一种空间相关系数,计算简单高效;在传统边坡安全监测重点考察单个测点的变形的情况下,挖掘不同空间位置测点之间变形的关联性,从关联性的角度来整体把握边坡的稳定状态,更加全面,对监测信息的数据挖掘更加充分;从前文提出的空间相关系数出发,针对边坡测点的关联性质提出测点关联度Rij、测点影响度Ii、边坡整体度I3个关联性指标,量化了边坡测点之间的关联性,有利于把握边坡整体性态,定位边坡关键部位。需要注意的是,本文提出的相关系数和对应指标仅仅对边坡的安全监测有一定辅助作用,不能直接反映边坡安全状态;此外,本文仅仅讨论这种相关系数在边坡外观变形监测中的应用,这种系数在其他监测项目中的进一步推广和改进仍有待研究。 [1] 温廷新, 张 波. 露天煤矿边坡稳定性的随机森林预测模型[J]. 科技导报, 2014, 32(4/5): 105-109. [2] SHARMA R K, MEHTA B S, JAMWAL C S. Cut Slope Stability Evaluation of NH-21 along Nalayan-Gambhrola Section, Bilaspur District, Himachal Pradesh, India[J]. Natural Hazards, 2013, 66(2): 249-270. [3] 张 豪, 罗亦泳. 基于人工免疫算法的边坡稳定性预测模型[J]. 煤炭学报, 2012, 37(6): 911-917. [4] 张均锋,丁 烨.边坡稳定性分析的三维极限平衡法及应用[J].岩石力学与工程学报,2005,24(3):365-370. [5] CHEN Z, WANG X, HABERFIELD C,etal. A Three-dimensional Slope Stability Analysis Method Using the Upper Bound Theorem Part I:Theory and Methods[J]. International Journal of Rock Mechanics & Mining Sciences, 2001, 38(3): 369-378. [6] 刘寒冰, 李国恒, 谭国金, 等. 基于时间序列的边坡变形实时预测方法[J]. 吉林大学学报(工学版), 2012,42(增1): 193-197. [7] 王艳霞. 模糊数学在边坡稳定分析中的应用[J]. 岩土力学, 2010, 31(9): 3000-3004. [8] 向超文,徐锦洪,李 焜,等.人工神经网络边坡稳定预报模型[J].工程地质计算机应用,2006,(1):1-9. [9] 杜 岩, 谢谟文, 吕夫侠, 等. 基于模态参量变化的边坡动态稳定分析新方法[J].岩土工程学报, 2015, 37(7): 1334-1339. [10]李南生, 唐 博, 谈风婕, 等. 基于统一强度理论的土石坝边坡稳定分析遗传算法[J].岩土力学, 2013, 34(1): 243-249. [11]王海军, 涂 凯, 闫晓荣. 基于果蝇优化算法的GRNN模型在边坡稳定预测中的应用[J].水电能源科学, 2015, 33(1): 124-126. [12]刘大有, 陈慧灵, 齐 红, 等. 时空数据挖掘研究进展[J]. 计算机研究与发展, 2013, 50(2): 225-239.[13]GAO T. Regional Industrial Growth: Evidence from Chinese Industries[J]. Regional Science and Urban Economics, 2004, 34(1): 101-124. [14]ANSELIN L. Spatial Econometrics: Methods and Models[M]. Dordrecht: Kluwer Academic, 1988. [15]ANSELIN L. Space and Applied Econometrics: Introduction[J]. Regional Science and Urban Economics, 1992, 22(3): 307-316. [16]宋马林, 王舒鸿, 汝慧萍. 一种新的考虑时间和空间的相关系数及其算例[J].数量经济技术经济研究, 2010, (7): 142-152. [17]COMBES P P. Economic Structure and Local Growth: France, 1984-1993[J]. Journal of Urban Economics, 2000, 47(3): 329-355. [18]ODLAND J. Spatial Autocorrelation[M]. London: SAGE Publications, 1988. (编辑:姜小兰) Application of an Improved Spatial Correlation Coefficient toExterior Deformation Monitoring of High Slope in Reservoir Area HU Tian-yi1,2, YOU Meng-tao2, LU Tian-lin3, WANG Cheng1, DONG An-yu1 (1.College of Water Conservancy and Hydropower,Hohai University,Nanjing 210098,China; 2.Water Conservancy & Water Transport Design Institute, Shanghai Municipal Engineering Design Institute, Shanghai 200092, China; 3.Shanghai Project Safety and Quality Supervision Center of Water Construction, Shanghai 200070, China) Conventional monitoring of reservoir slope is mainly focused on the deformation and stress changes of single point rather than the overall deformation with multiple points. In view of this, an improved spatial correlation coefficient is proposed to calculate the spatial correlations among multiple points of slope. The present coefficient is based on Pearson’s correlation coefficient and Moran’s correlation coefficient, and takes the spatial coordinates of different measuring points into consideration. Three relevance indexes of exterior deformation of slope are proposed, namely relevance degreeRijof measuring point, influence degreeIiof measuring point, and integrity degreeIof slope. The overall state of slope can be obtained according to the variation trends of the indexes. The present coefficient is applied to analyzing the deformation data of the high slope of a concrete dam, and the results prove that the coefficient presented in this paper is practical and rational for analyzing the safety of slopes. high slope; exterior deformation monitoring; Pearson’s correlation coefficient; Moran’s correlation coefficient; spatial correlation coefficient 2016-03-25; 2016-04-25 国家自然科学基金重点项目(41323001);高等学校博士学科点专项基金(20120094110005);江苏省杰出青年项目(BK20140039);水利部土石坝破坏机理与防控技术重点实验室基金项目(KY914002);江苏省2015年度普通高校研究生科研创新计划项目(KYXX15_0140,KYXX15_0138) 胡添翼(1991-),男,江苏南通人,硕士研究生,研究方向为大坝安全监测,(电话)0513-82594383(电子信箱)htyandy@me.com。 10.11988/ckyyb.20160273 2017,34(7):41-47,53 TV698.1 A 1001-5485(2017)07-0041-07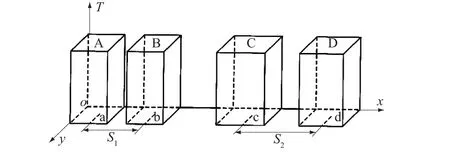
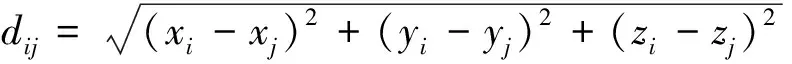
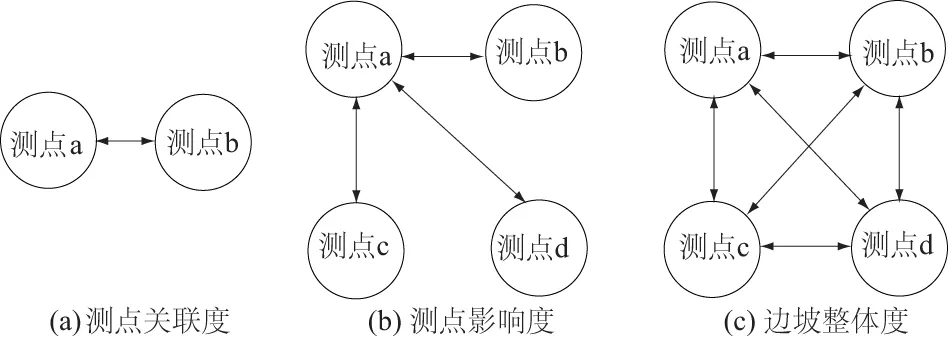
4 空间相关系数在边坡安全监测中的应用
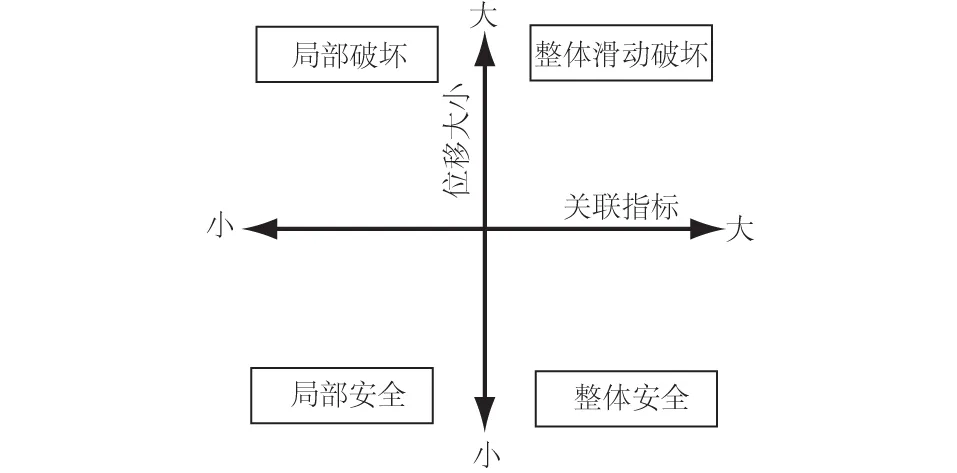
5 工程实例


6 结 语
——工程地质勘察中,一种做交叉剖面的新方法

