一种面向工程的局部RCS检测算法研究

徐 涛，王德毅

(沈阳航空航天大学 自动化学院，辽宁 沈阳 110136)

一种面向工程的局部RCS检测算法研究

徐 涛，王德毅

(沈阳航空航天大学 自动化学院，辽宁 沈阳 110136)

飞行器的蒙皮在服役期间容易产生腐蚀或破损进而增大飞行器的雷达散射截面，因此需要对修复后的区域进行局部雷达散射截面(Radar Cross-Section，RCS)检测以评估修复效果。研究了一种面向工程的近远场变换算法以实现对修复区域的RCS检测，该算法基于球面波环式展开算法，并在传统近远场变换算法的基础上使用渐进式代替传统的汉克尔函数，设计了一种适用于工程应用的近远场变换算法。使用HFSS和Matlab软件对设计的算法进行了仿真验证，结果表明算法能够求得修复后局部小区域的RCS。

雷达散射截面检测；蒙皮破损；近远场变换；汉克尔函数

Abstract Corrosions or damages often happen on the coating system of aircrafts,and the repairing process may enlarge the Radar Cross Section of aircrafts.In that case,it is necessary to conduct a partial RCS scanning on the repaired places in order to evaluate the maintenance effectiveness.This paper discusses a near-field-to-far-field transformation algorithm to realize the RCS detection of the repaired place.The conventional Hankel function is substituted by an approximation algorithm which is more suitable for application.The simulation results by HFSS and Matlab show the effectiveness of the algorithm.

Key words RCS detection;coating failure;near-field-t-far-field transformation;Hankel function

0 引言

飞行器蒙皮是飞行器的重要组成部分，飞行器在使用过程中会遇到各种不同的环境因素。美军评价F-18飞机涂层的环境谱中包含了湿热暴露试验、紫外线照射试验、热冲击试验、低温疲劳试验和盐雾试验等[1]。飞行器在服役期间会出现蒙皮受损，如破洞、划伤和开裂等，这些损坏大大地增大了飞行器的雷达散射截面。工程实践中使用了各种各样的修补方式，如铆接修理和加强板修理、止裂孔等[2]。现役先进隐身战机的隐身性能主要体现在目标对于雷达波的隐身，即雷达散射截面(Radar Cross-Section，RCS)的大小[3]。因此，当飞行器蒙皮修复完毕之后，对修复处进行RCS快速检测是十分必要的。目前对于RCS的检测手段主要分为近场检测与远场检测2种[4]。远场由于对场地要求高不易适用于现场评估。近场测量又分为平面采样、柱面采样和球面采样3种。球面采样最为精确[5]，但因为采样耗时最长而难以应用在实时的工程应用场合。

Lahaie I. J.[6-7]提出了一种可靠的球面波环式扫描近远场变换方法，实现了在近场使用一维环式扫描获得的近场数据求得目标体远场散射数据。另外，Lahaie I. J.[8]还论证了该方法在非全角度扫描下获得可靠的远场数据以进行检测RCS的可行性。

由于Lahaie I. J.的理论算法中使用了特殊函数(Bessel函数、Hankel函数)，在仿真环境下该函数由软件系统进行了封装，无法移植性到其他系统，不方便工程应用。因此，本文推导了近远场变换的步骤，在仿真分析过程中对特殊函数进行逼近，将球面波环式扫描近远场变换算法进行了简化。在算法仿真时，采用一个微带天线进行破损模拟。

1 近场远程变换算法

本文算法思想是通过对近场球面波回波函数和近场场强的乘积求和，其中近场检测指的是在辐射近场区，即

(1)

式中，λ为微波的波长；D待测目标的实孔径[9]。

再对波数求导构建近场球面波回波函数与远场平面波回波函数的联系，实现球面波的近远场变换。使用ISAR(Inverse Synthetic Aperture Radar)检测方式对目标体进行环式扫描检测，该方式主要以待测目标固定不动，发射天线以扫描半径围绕目标体做圆周运动的方式进行扫描检测，示意图如图1所示。

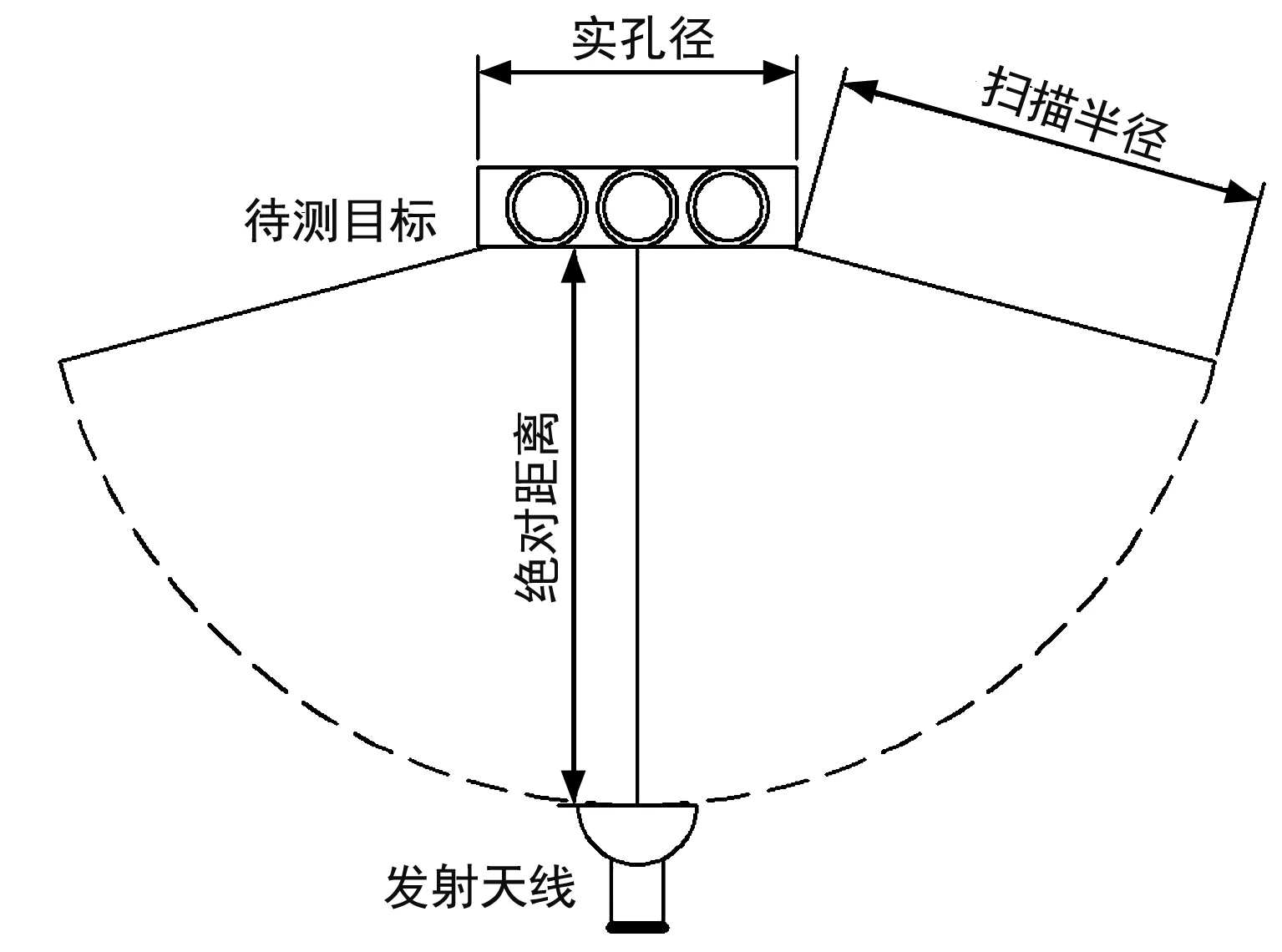
图1 近场球面波环式近远场变换局部扫描示意

1.1 近场数据预处理

空间点散射体近场回波函数为Green函数：

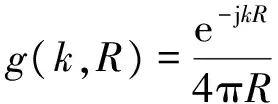
(2)

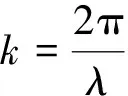
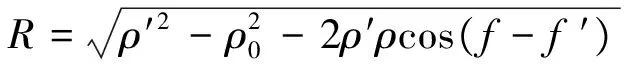
(3)

为探头到散射点的绝对距离。

那么探头作为接收天线，在不考虑探头补偿的情况下，探头接收的近场回波函数为：

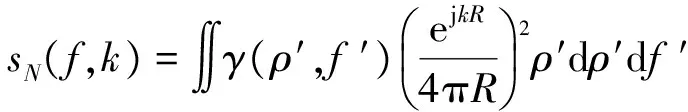
(4)

式中，γ(ρ′,f′)是散射点的近场场强分布函数，将sN(f,k)对波数k求导得：

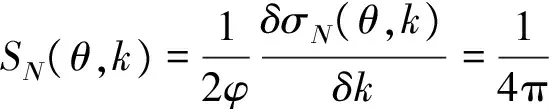
(5)

为使计算简便，将式(4)转化为对频率和对距离的2次傅里叶变换的形式：

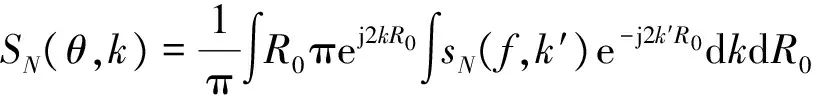
(6)

有柱面波转换式：

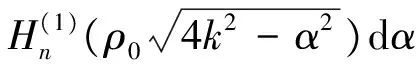
(7)

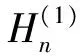
在工程应用中，当4k2>>α2时,

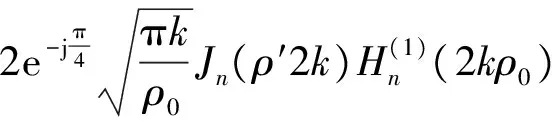
(8)

改变式(5)的积分对象后可变为：

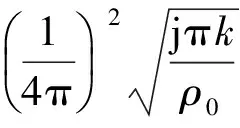
(9)

文献[10]中对汉克尔第一类函数的零阶进行了如下渐进：

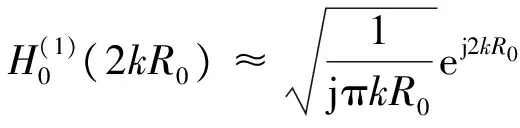
(10)

于是式(9)可进一步转化为：

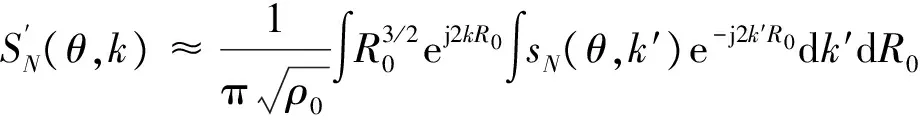
(11)

即为预处理后的近场数据。

1.2 远场数据处理

散射点在远场的回波信号可以看成是平面波，其远场散射函数可以等效为：

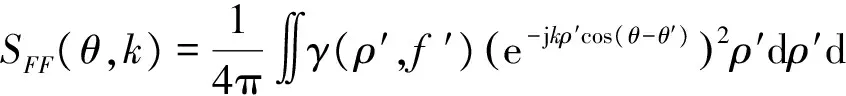
(12)

又因为

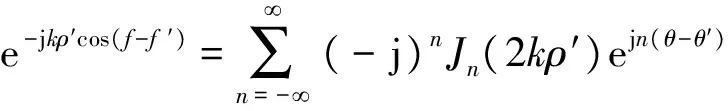
(13)

于是有

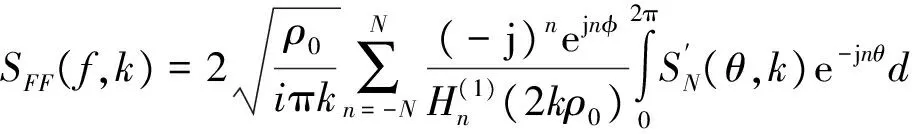
(14)

因为室内近场多采用ISAR模式采样，对式(13)中的近场部分进行一维离散傅里叶变换，得

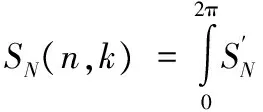
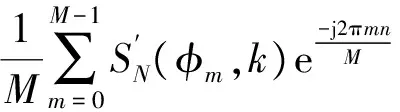
(15)

于是，针对每一个采样点的回波信号，可得

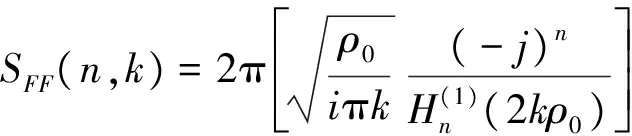
(16)

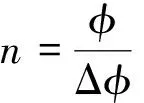
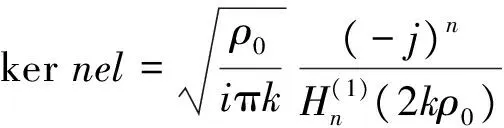
(17)

相卷积得出远场分布。

由于式(17)中理论算法中使用了Bessel函数和Hankel函数，Hankel函数属于特殊函数[11]，其在进行软件仿真过程中，这2个特殊函数都是由软件系统封装，使得在实际应用环境下无法直接移植，不方便应用。本文从工程应用的角度对Hankel的核函数进行了适当的逼近，以提高算法的可移植性。

文献[12]中的第一类Hankel逼近表达式为：

(18)

可将式(17)带入式(16)，得到的核函数为：

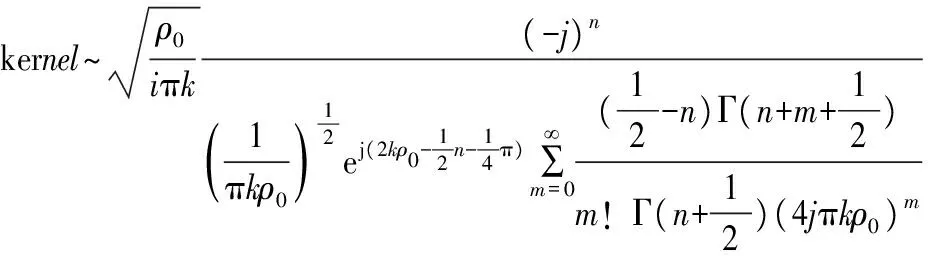
(19)

由式(19)可见，如果将含有特殊函数的核函数逼近为由Gamma函数组成的核函数，将使得编程更容易实现。

最终，对于每个采样点上获得的近场数据的处理函数为：

SFF(n,k)=2π[kernel]*SN(n,k)。

(20)

将式(14)带入式(19)，即可求得对应角度的远场分布。再将式(19)的结果带入下面的RCS公式：

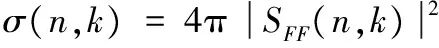
(21)

即可求得远场RCS值。

2 算法仿真分析

根据王培凌、周昊等[13-14]采用的破损结构模型，可以认为修补区域大小应为r=25.5 mm的破洞。因此，本文采用面积相近的中心频率在2.45GHz的微带天线进行电磁仿真。因HFSS是业界公认的三维电磁场设计和分析的工业标准[15]。本文使用HFSS对微带天线进行建模如图2所示。中心区域为金属导体，模拟破损的修复区域。

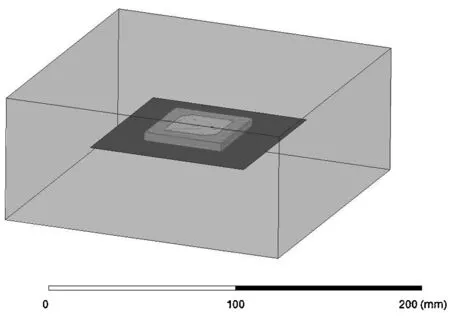
图2 微带天线HFSS模型

微带天线的远场场强三维分布如图3所示。

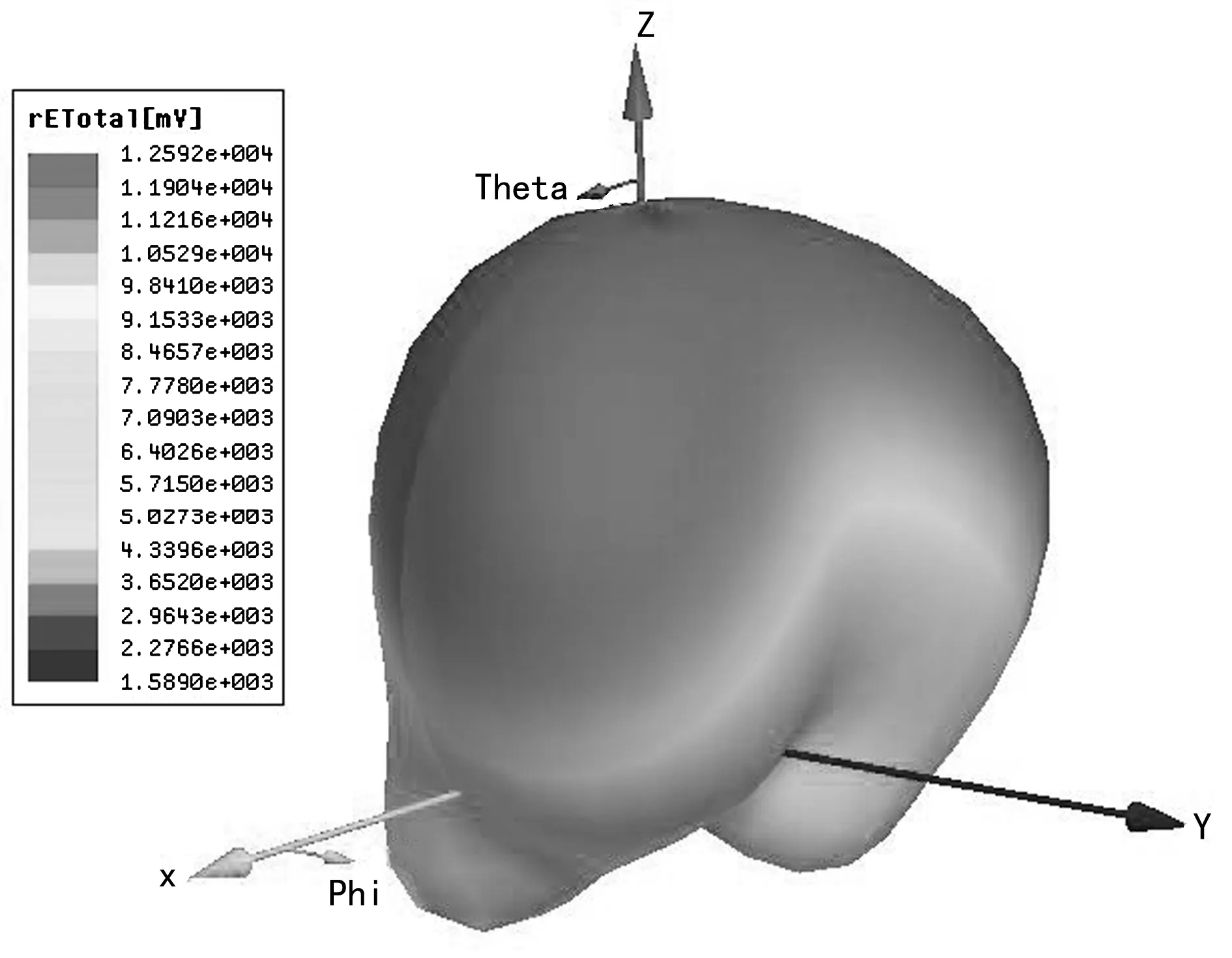
图3 远场电场三维分布

可以看出，该天线的主瓣区域主要集中在方位角为-75°～75°的区域，也是该天线辐射特征最明显的范围。使用近远场变换得到的远场电场与理论远场电场的对比如图4所示。

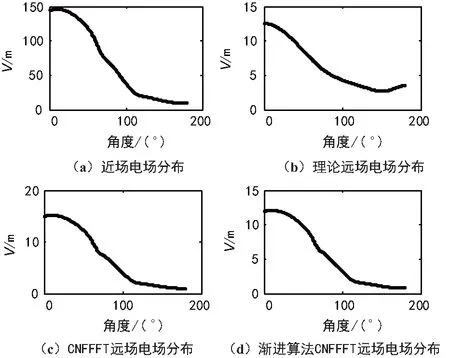
图4 2种算法与近场远场场强的比较

根据获得的近场数据，通过近远场变换得出渐进前和渐进后的算法的远场分布并将其进行对比，可以发现图4(b)、图4(c)和图4(d)三者相幅值和包络接近，证明该算法可行。渐进算法和通过理论远场场强获得的远场RCS的对比图。

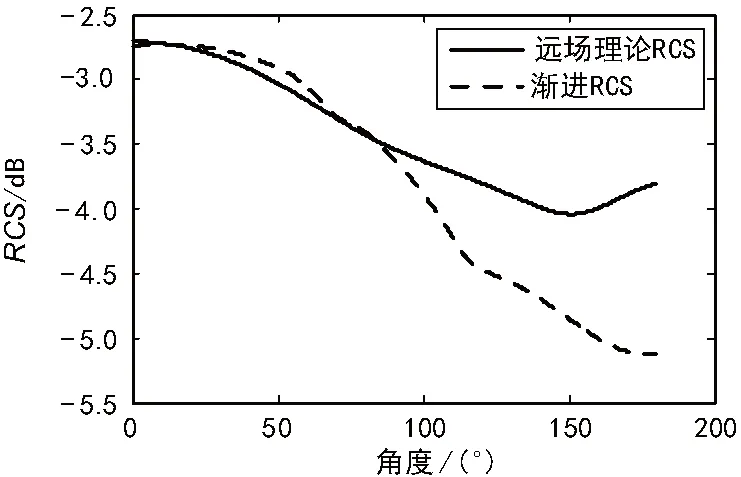
图5 球面波环式近远场变换与远场的对比

仿真结果表明，改进算法和HFSS生成的理论远场分布曲线在0°～100°区域十分接近，在100°～180°最大差约为1.3 dB。由于飞行器的隐身特性主要体现在对雷达的前向隐身[16]，并且辐射特征主要是由散射的主瓣体现的。因此可以认为该算法可以在工程应用中使用。

3 结束语

本文通过数学手段对波数求导等手段实现了球面波与平面波之间的联系，推导出了球面波环式扫描近远场变换算法。使用渐进式后的核函数显然具有更好的可编程性。使用Matlab和HFSS软件求出一个模拟蒙皮破损区域大小的微带天线的近场远场电场特征。使用算法求解出其局部远场方向图，并将其与理论值进行了对比。通过仿真对比可以看出，渐进算法在主瓣区域具有较高的准确性，验证了该算法具有较高的工程应用价值。

未来工作将主要集中在针对低辐射能量区域的误差补偿和对更复杂模型的RCS检测上。完善该算法在复杂条件下的精确性。

[1] 张蕾,陈群志,刘慧丛,等.飞机外部IMR21纳米复合涂层在典型加速腐蚀环境中的腐蚀失效行为[J].表面技术,2014,43(2):36-41.

[2] 代永朝,郑立胜.飞机结构检修[M].北京:航空工业出版社,2006.

[3] 阮颖铮.雷达截面与隐身技术[M].北京:国防工业出版社,1998.

[4] 王玖珍,薛正辉.天线测量实用手册[M].北京:人民邮电出版社,2013.

[5] 张麟兮.雷达目标散射特性测试与成像诊断[M].北京:中国宇航出版社,2009.

[6] LAHAIE I J.Overview of an Image-based Technique for Predicting Far-field Radar cross Section from Near-Field Measurements[J].IEEE Antennas and Propagation Magazine,2003,45(6):159-169.

[7] LAHAIE I J,COLEMAN C M,RICE S A.An Improved Version of the Circular Near Field-to-far Field Transformation(CNFFFT)[C]∥Proceedings of the 27th Annual Meeting of the Antenna Measurement Techniques Association(AMTA’05),2005:196-201.

[8] RICE S A,LAHAI I J.A Partial Rotation Formulation of the Circular Near-field-to-far-field Transformation(CNFFFT)[J].IEEE Antennas and Propagation Magazine,2007,49(3):209-214.

[9] 丁君.高等学校教材:工程电磁场与电磁波[M].北京:高等教育出版社,2005.

[10] FISCHER B E,LAHAIE I J,FLISS G G.On the Use of Wavenumber Migration for Linear SAR Image Formation and Near-field to Far-field RCS Transformation[C]∥Proceedings of 23rd Annual Meeting of the Antenna Measurement Techniques Association(AMTA’01),2001:117-122.

[11] 王载舆.数学物理方程及特殊函数[M].北京:清华大学出版社,1991.

[12] SEKELJIC N.Asymptotic Expansion of Bessel Functions;Applications to Electromagnetics[C]∥Dynamics at the Horsetooth,2010:1-12

[13] 周昊,殷之平,刘嘉鹏,等.典型飞机蒙皮破损结构损伤容限研究[J].飞机设计,2016(2):30-33.

[14] 王培凌,王培群.飞机蒙皮腐蚀试验及分析[C]∥ 2015航空试验测试技术学术交流会,2015:176-185.

[15] 徐兴福.HFSS射频仿真设计实例大全[M].北京:电子工业出版社,2015.

[16] 马井军,赵明波,张开锋,等.飞机隐身技术及其雷达对抗措施[J].国防科技,2009(3):38-44.

A Project-oriented Local RCS Detection Algorithm

XU Tao,WANG De-yi

(AutomationDepartment,ShenyangAerospaceUniversity,ShenyangLiaoning110136,China)

10.3969/j.issn.1003-3106.2017.08.19

徐涛，王德毅.一种面向工程的局部RCS检测算法研究[J].无线电工程,2017,47(8):79-82.[XU Tao,WANG Deyi.A Project-oriented Local RCS Detection Algorithm[J].Radio Engingeering,2017,47(8):79-82.]

2016-12-08

TN955

A

1003-3106(2017)08-0079-04

徐 涛 男，(1971—)，副教授。主要研究方向：RCS测试技术、新型传感技术。

王德毅 男，(1989—)，硕士研究生。主要研究方向：RCS测试技术。