基于K-邻居节点覆盖的物联网定位模型①

徐世武

(福建师范大学 协和学院信息技术系, 福州 350117)

基于K-邻居节点覆盖的物联网定位模型①

徐世武

(福建师范大学 协和学院信息技术系, 福州 350117)

针对传统基于接收信号强度的定位缺陷, 提出一种新型的基于K-邻居节点覆盖的物联网定位模型. 该模型分为选取邻居节点与定位两个阶段, 未知节点先通过调整发射功率等级来选择最近的K个邻居节点, 尽量减少远距离节点对定位的影响. 定位阶段, 未知节点通过与K个信标节点的接收信号强度来计算权重, 通过加权求和算出未知节点的坐标. 采用K-邻居节点误差的自校正方法对坐标进行补偿. 该定位模型可有效的避免环境因素对定位的影响, 且定位算法简单, 避免复杂的计算. 实验表明, 该定位模型定位精度较高.

接收信号强度; 定位; 物联网; 无线传感器网络; 误差自校正

物联网(IOT: The Internet of Things)技术是近几年备受关注的新兴研究领域, 物联网可以实现人与人, 人与物, 物与物的互联互通, 因此可以广泛应用于智能医疗, 智能交通, 智能家居, 航空航天等领域[1,2]. 无线传感器网络(WSN)作为IOT的核心技术之一, 近几年也得到不断的发展, 且针对WSN定位技术的研究也是IOT诸多定位模型研究的主要技术之一[3].

常见的室内测距技术有接收信号强度(RSSI)、到达角度(AOA)以及到达时间(TOA)等[4-6]. AOA技术在规模较大的网络中计算复杂度相对较高, TOA利用信号的传播速度与时间计算距离, 精度较高, 前提要求高精度的时间同步, 且硬件成本较高. RSSI技术对节点时间同步要求低, 不需要增加硬件辅助设备, 算法实现简单, 成本低, 因此主要的室内测距技术采用的是RSSI[6-11].传统的基于RSSI的定位技术有极大似然定位法与质心定位法等, 极大似然定位法受到无线电传播路径损耗模型影响较大, 质心定位法权重相等的情况下, 误差较大, 因此我们可以采用加权的质心定位法, 未知节点获取不同信标节点的RSSI值, 根据RSSI值的大小来判断对应信标节点的权重因子, 不但降低了无线电传播模型的影响, 也较大提高了质心定位法的精度.

1 传统的定位模型

传统的定位模型分为基于测距与无需测距两种,基于测距定位需要先计算未知节点与信标节点的距离,然后通过三边定位法或极大似然法计算未知节点的坐标. 采用传统的无线电传播路径损耗模型估算盲节点与信标节点的距离, 如式(1)所示[10]. 在信标节点已知的发射信号强度下, 盲节点根据接收到的信号强度, 通过两者的信号强度差可以估算出两者之间的距离. 式(1)中RSSI(d)表示距离为d处的接收信号强度,RSSI(d0)表示距离为d0处的接收信号强度, d0一般取1米[9,10]. λ表示路径损耗模型, 与实际环境相关. ζσ一般满足高斯随机分布.

无线电传播路径损耗模型较复杂, 很难得到统一的损耗模型, 不同的环境模型差别较大, 且需要事先大量采集信息获取模型参数, 能耗较大. 因此采用式(1)估算节点距离极易受到环境因素的影响, 通过极大似然估算的坐标容易产生误差叠加的情况, 且算法相对较复杂.

无需测距的定位模型主要有质心定位法, 如式(2)所示[9], 当未知节点(xi, yi)获得N个信标节点后, 取N个信标节点的质心为定位的坐标值, 采用式(2)计算坐标算法简单, 容易实现, 误差波动大.

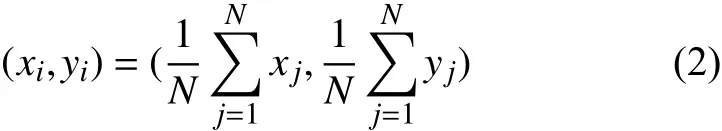
本文采用无需测距的定位模型, 在传统质心定位法的基础上, 利用节点接收信号强度随距离增大而减小这一趋势, 通过未知节点与信标节点的接收信号强度来计算对应的权重, 提高质心定位法的定位精度.

2 基于K-邻居节点覆盖(K-NNC)的加权质心定位算法

2.1 算法描述

N个信标节点有规则的布置在待定位的区域内, 信标节点的坐标与对应的节点编号可以事先获取. 当未知节点在信标节点构成的定位区域(如大型医院, 大型地下停车场)内移动的时候, 因为无线传感器节点的发射功率等级可以调整(本实验采用八个功率等级), 首先节点以最小的发射功率广播定位信息, 当收到K个1跳节点的反馈信息, K不满足4个的时候, 盲节点加大发射功率, 直到K大于等于4个为止. 对盲节点接收到信标节点的信号强度排序, 选取前K个信号最强的节点做为盲节点的最近邻居节点.

定义1. 邻居节点, 表示未知节点在对应发射功率等级下, 1跳通信内的信标节点集合.

定义2. 接收信号强度Sij, 表示第i个未知节点接收到第j个邻居信标节点的信号强度. 如式(3)所示.

如果采用传统的质心定位算法来求解, 虽然不用估算距离, 但可能盲节点偏离质心较远, 计算误差会非常大. 因此我们应该采用加权求和方式求解, 如式(4)与式(5)所示. 表1为本文在真实的室内环境下测得的未知节点与不同距离信标节点的接收信号强度平均值. 从表1可以看出对于未知节点测得与信标节点的接收信号强度S越大, 间接反应了未知节点与对应的信标节点越近, 接收信号强度越大的节点通过式(5)可以获得越大的权重. 采用式(5)的缺陷是当未知节点与信标节点较远时, 未知节点接收到的信号强度dBm会出现负值,可以利用单位转换, 将接收信号强度dBm转换为功率mW计算权重wi. 采用式(4)的加权求和无需测距, 算法复杂度低, 功耗低.

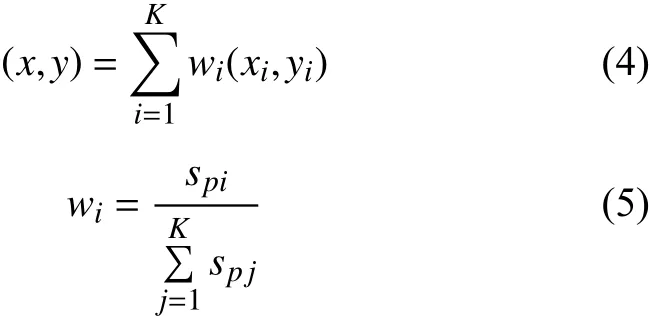
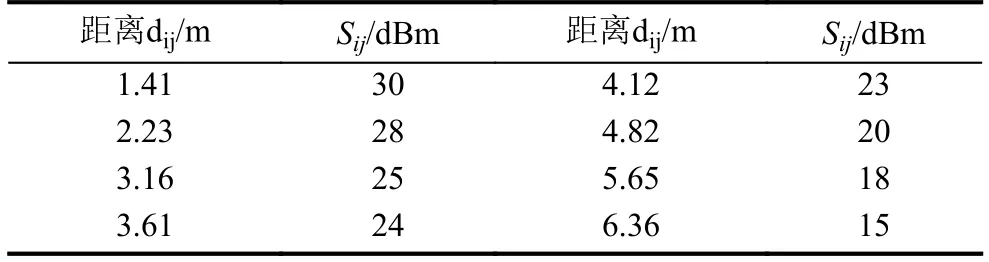
表1 距离与接收信号强度关系

2.2 K-邻居节点误差的自校正

因在实际的环境中, 无线电传播路径损耗会受到多径衰落、障碍物等影响, 因此不同区域的路径损耗模型不一样, 即使同样的区域也可能受到环境变化, 如雨天等影响. Sij未必能够准确的反映出信号的衰减程度, 因此应该对式(4)计算的坐标进行修正补偿, 为了降低区域性对定位结果的影响, 可以将选举出来的K(本文实验采用4个)个邻居信标节点当成未知节点进行定位. 因信标节点的位置以及之间的距离事先知道, 可以根据K邻居节点的实际坐标与采用式(4)计算的坐标进行最优线性拟合, 通过拟合的方程对盲节点的定位结果进行补偿.

定义3. 坐标(Xi, Yi), i=1, 2…, K, 表示选举出来K个信标节点的实际坐标.

定义4. 坐标(Xi’, Yi’), i=1, 2…, K, 表示选举出来K个信标节点当成盲节点, 并通过式(4)计算的坐标.

通过定义3与定义4, 我们可以对选举出来的K个信标节点的X坐标与Y坐标分别进行线性拟合. 给出K对实验数据, 将这些数据带入式(6)然后做差, 如式(7)所示. 要使偏差R最小, 即所有数据偏差的平方和R2最小, 分别对aj与mj求导, 整理公式后得到式(8). 通过式(8)可以得到K个信标节点X坐标的补偿系数aj与mj.我们可以采用同样的方式对K个信标节点的Y坐标进行线性拟合. 得到K个信标节点Y坐标的补偿系数bj与nj.则我们可以得到盲节点经过K邻居信标节点自校正补偿后的坐标(x, y)如式(11)所示, 式(11)中是盲节点通过式(4)加权求和的坐标.

3 实验分析

3.1 实验环境

硬件: 采用德州仪器(TI)的CC2530为主控芯片的节点. 操作系统: TinyOS(加州大学伯克利分校开发的专为嵌入式无线传感网络设计的开放源代码操作系统). 语言: nesC语言. 编译环境: cygwin.

3.2 实验结果分析

定义5. 定位误差E, 假设定位节点的实际坐标为(x0, y0), 计算坐标为(x, y), 则定位误差E如式(12)所示.

表2 定位算法性能比较(K=4)

从表2可以看出, 在相同的实验环境下, 当K等于4的时候, K-NNC算法定位误差E明显小于传统加权质心定位算法, 传统加权质心定位算法当盲节点偏移质心较远时误差将非常大. 而K-NNC算法虽然误差也会随盲节点偏移质心而变大, 但K-NNC算法考虑了权重,因此增大并不明显. 在相同实验环境中, K-NNC算法经过选举出来的K个邻居信标节点误差自校正后, 可以有效的降低环境因素的影响, 相比于校正前, 误差E明显降低. 为了更加直观的比对算法, 我们采用MATLAB软件绘制了5个盲节点的误差E, 如图1所示. 从图1可以看出采用自校正补偿的K-NNC算法性能得到显著提高.为了更加充分的比对几种算法, 我们取不同的K值进行比对E, 通过节点编号3进行试验测试, 从表三可以看出经过修正后的K-NNC算法

当K值为4的时候误差E就很小. 从表3与图2可以看出, 当K取4的时候误差E明显小于K取3的值, 而当K取更大值的时候, 传统加权质心算法并不会因为K值变大精度而提高, K-NNC算法虽然修正前, 修正后的误差E有所改善, 但并没有比K取4的时候有明显提高. 反而但K值取过大的时候增加通信代价与通信干扰. 因此当K的值取4的时候为较理想的值.

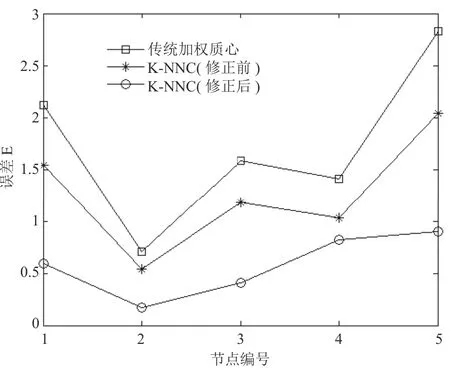
图1 不同节点编号的误差E分布图(K=4)

图2 不同K值的误差E分布图(节点编号3)

表3 不同K值的误差E(节点编号3)

4 结束语

物联网技术在很多应用场合中, 不知道节点的位置信息是没有意义的, 因此对定位系统的研究非常重要. 本文在传统质心定位法的基础上, 提出一种基于邻居信标节点误差自校正的K-NNC定位算法. K-NNC定位算法根据盲节点与信标节点的接收信号强度来决定权重的大小. K-NNC定位算法选举的信标节点为最近邻的K个信标节点, 因此可以有效避开不同环境对结果的影响. 在相同的实验环境中, 通过对K个信标节点拟合出最优的线性, 通过拟合出来的线性关系对计算坐标进行补偿, 最大程度避免了环境因素的影响. K-NNC定位算法的定位复杂度低, 定位精度高.

1Atzori L, Iera A, Morabito G. From “smart objects” to“social objects”: The next evolutionary step of the Internet of Things. IEEE Communications Magazine, 2014, 52(1):97–105. [doi: 10.1109/MCOM.2014.6710070]

2Xu LD, He W, Li SC. Internet of things in industries: A survey. IEEE Trans. Industrial Informatics, 2014, 10(4):2233–2243. [doi: 10.1109/TII.2014.2300753]

3顾晶晶, 陈松灿, 庄毅. 基于无线传感器网络拓扑结构的物联网定位模型. 计算机学报, 2010, 33(9): 1548–1556.

4肖竹, 谭光华, 李仁发, 等. 无线传感器网络中基于超宽带的TOA/AOA联合定位研究. 计算机研究与发展, 2013, 50(3):453–460. [doi: 10.7544/issn1000-1239.2013.20110029]

5Li B, Wang WJ, Yin QY. A distributed localization in wireless sensor networks utilizing AOD estimation and synthetical uniform circular array. Science China Information Sciences, 2015, 58(6): 062307.

6钱志鸿, 孙大洋, Leung V. 无线网络定位综述. 计算机学报, 2016, 39(6): 1237–1256. [doi: 10.11897/SP.J.1016.2016.01237]

7周艳, 李海成. 基于RSSI无线传感器网络空间定位算法. 通信学报, 2009, 30(6): 75–79.

8罗炬锋, 邱云周, 付耀先, 等. 研究片内多径分离技术在基于RSSI定位中的应用 .电子与信息学报 ,2011 ,33(4) :891–895.

9韩东升, 杨维, 刘洋, 等. 煤矿井下基于RSSI的加权质心定位算法. 煤炭学报, 2013, 38(3): 522–528.

10崔法毅, 邵冠兰. 基于RSSI多边定位误差的加权质心定位算法. 红外与激光工程, 2015, 44(7): 2162–2168.

11Moragrega A, Closas P, Ibars C. Potential game for energyefficient RSS-based positioning in wireless sensor networks.IEEE Journal on Selected Areas in Communications, 2015,33(7): 1394–1406. [doi: 10.1109/JSAC.2015.2430172]

Location Model Based on K-Neighbor Node Coverage for IOT

XU Shi-Wu
(Concord College Department of Information Technology, Fujian Normal University, Fuzhou 350117, China)

In view of the traditional positioning defects based on

signal strength, a new K-NNC location algorithm is proposed for IOT, based on K- neighbor node coverage (K-NNC). K-NNC is divided into two stages, select neighbor nodes and positioning stage. In order to reduce the influence of long distance nodes on the positioning, by adjusting the transmit power to select the nearest K neighbor node. In positioning stage, the node calculates the weight by the received signal strength of the K beacon node. The coordinates of the nodes are calculated by the weighted sum. Using the self-correcting method the position coordinates are compensated. The K-NNC positioning model can effectively avoid the influence of environmental factors on the positioning, and the positioning algorithm is simple. Experiment shows the K-NNC positioning model positioning is highly accurate.

received signal strength; location; IOT; WSN; error self-correction

徐世武.基于K-邻居节点覆盖的物联网定位模型.计算机系统应用,2017,26(7):269–272. http://www.c-s-a.org.cn/1003-3254/5866.html

福建省教育厅科技项目(JA13368, JAT160667, JB13263); 福建师范大学协和学院教学改革研究项目(JG20140207)

2016-11-04; 收到修改稿时间: 2017-01-04