基于聚类的城市共同配送海量订单调度问题研究①

谢天保, 赵 萌, 雷西玲

1(西安理工大学 经济与管理学院, 西安 710054)

2(西安理工大学 计算机科学与工程学院, 西安 710054)

基于聚类的城市共同配送海量订单调度问题研究①

谢天保1, 赵 萌1, 雷西玲2

1(西安理工大学 经济与管理学院, 西安 710054)

2(西安理工大学 计算机科学与工程学院, 西安 710054)

针对云物流环境下城市共同配送海量订单调度难的问题, 本文提出基于订单聚类的调度算法. 首先针对单中心多车辆调度问题, 提出基于单亲遗传的优化调度算法; 在此基础上综合考虑城市配送中心的地理位置、车辆及配送点的地理位置、货物的种类、需求量, 提出采用蚁群算法构建基于配送中心的海量订单聚类、优化调度算法.

共同配送; 海量订单; 聚类; 蚁群算法; 调度

1 引言

随着信息技术的高速发展, 我国的城市物流配送正在进行着变革, 传统的物流配送已经不能满足现代城市物流发展的需求, 加快物流信息的共享互通、降低物流成本、统筹优化社会物流资源、提高城市物流配送效率是新环境下城市物流配送亟需解决的问题.而云物流是基于云计算强大的通信能力、运算能力和匹配能力[1], 建立物流信息共享平台, 实现智能匹配、智能组合、智能管理物流服务等先进功能[2]. 基于云物流的物流信息共享平台, 是对整个物流网络中的信息进行收集、处理、传递、共享的集中地, 其主要思想就是: 在物流信息充分共享的前提下, 对供货方和收货方之间交易的海量物流订单、各类企业和第三方物流企业现有的零散物流资源进行整合, 依靠云计算技术对这些信息进行处理和挖掘, 实行科学合理的订单规划和车辆调度进行管理, 实施共同配送, 使得共同配送信息平台的各方参与者都能获取更多的利益, 从而吸引更多企业的物流订单和物流资源加入到平台中, 形成一个平台开放、资源共享、终端无限的网络. 因此,研究云物流下城市共同配送海量订单调度问题, 有效缓解城市交通压力、减少城市污染, 对提高城市物流管理水平、改善城市居民的生存环境具有重要的意义,也对云物流信息共享平台的实际建设与应用具有推进作用.

物流配送车辆优化调度问题最早由DnaZtig和Ramser于1959年首次提出[3]. 车辆优化调度问题根据时间特征的差异可分为车辆路径规划问题VRP(Vehicle Routing Problem)、车辆调度问题VSP (Vehicle Scheduling Problem)以及有时间窗的车辆路径问题VRPTW(Vehicle Routing Problem with Time Windows)[4], 属于一个NP-hard问题, 其模型建立针对一个配送中心而且只有当其规模较小时, 才能求其精确解. 而对于多中心协同配送调度问题, 在以往的国内外研究中[5-11], 文献[5-6]首先将多车场问题转化为单车场问题, 用分解算法处理多车场配送问题; 文献[7]提出了一种基于网络流模型最优解的启发式算法, 来探讨多车场满载货运车辆的优化调度问题; 文献[8]运用了禁忌搜寻法解决车辆配送路线问题; 文献[9]采用了C-W节约算法对有时间窗约束的非满载车辆调度进行路线安排; 文献[10]提出用神经网络算法来求解车辆配送路线优化问题; 文献[11]建立了一种基于最小配送费用的数学模型来研究多车场多车型车辆调度问题, 并借助遗传算法对模型进行求解. 云物流模式下城市共同配送涉及到海量订单、众多配送中心以及各种类型车辆调度, 再加上多种约束条件(时间窗约束、类别), 显然是一个复杂的NP-Hard问题, 同时考虑到云物流模式下的订单配送具有多频次、少批量、多品种、零散化、个性化、订单动态性、时效性高、随机性强等特点, 这些特点无疑增加了云物流海量订单调度模型求解的复杂性,为此本文提出基于多中心聚类结合单中心多车辆调度算法实现海量订单的优化调度, 根据物流订单的特性(物流中心空间距离、货物类型等)采用聚类分析[12], 分别计算各中心(类)的配送成本, 以上过程结合改进蚁群算法对海量订单反复迭代聚类分析, 最终可求取城市海量物流订单的最优调度方案, 便于云物流分布式调度的实现.

2 基于聚类的海量订单共同配送调度模型

假设某城市现有物流中心M个, 用变量m(m=1, 2,…, M)表示, 考虑到城市居民需求的动态性, 这些物流配送中心在城市区域均匀分布, 其坐标为(Xm, Ym), 每个物流中心拥有多个不同类型的运输车辆, 平均车速V, 物流中心的地理信息、及车辆信息通过云服务收集于城市共同配送云物流平台. 在某一时刻(通常周期性处理), 城市物流平台收集到N个订单, 货物配送点随机分布于城市覆盖区域, 根据M个配送中心的地理位置信息、各自的车辆信息、配送点地理位置信息, 如何从M个配送中心选择出若干个配送中心及车辆负责海量订单的配送任务, 合理调度车辆资源、提高运输车辆的配载率, 缓解城市交通拥堵, 降低城市物流配送成本是本文研究的目标.

2.1 问题分析及变量说明

在云物流城市共同配送模式下, 配送的总成本主要包括固定成本和运输成本. 固定成本包括车辆动用成本和人力资源成本等, 在基于时间窗约束车辆调度[13]的数学模型中, 这里采用硬时间窗, 即必须在规定时间段送达. 下面首先对模型中的变量进行说明, 然后分析城市共同配送活动的成本.

(1) 配送中心信息描述:

m(m=1, 2, …, M)表示配送中心编号;

(Xm, Ym)(m=1, 2, …, M)表示配送中心m的地理坐标;

f(m, k)(m=1, 2, …, M, k=1, 2, …, K)表示配送中心m的车辆编号;

g(f(m, k))(m=1, 2, …, M, k=1, 2, …, K)表示m配送中心第k辆车的最大载重量;

C(f(m, k))(m=1, 2, …, M, k=1, 2, …, K)表示m配送中心第k辆车固定成本(包括人力成本);

UC(f(m, k))(m=1, 2, …, M, k=1, 2, …, K)表示m配送中心第k辆车每公里消耗成本.

(2) 配送点信息描述:

n(n=1, 2, …, N, N＞＞M)表示配送点编号;

(Xn, Yn)(n=1, 2, …, N)表示配送点n的地理坐标;

Pg(n)(n=1, 2, …, N)表示配送点n所需货物的重量;

Tp(n)(n=1, 2, …, N)表示配送点n所需货物的类别,不同类别的货物不能同车, 例如蔬菜和农药;

st(n)(n=1, 2, …, N)表示配送点n要求送货的最早时间;

et(n)(n=1, 2, …, N)表示配送点n要求送货的最迟时间;

tt(n)(n=1, 2, …, N)表示配送点n卸货消耗时间;

D(i, j)(i=1, 2, …, N, j=1, 2, …, N)表示配送点i和配送点j之间的距离;

DHS(i, m)表示配送点i和配送中心m之间的距离.

(3) 决策变量:

a) 配送点i是否为配送中心M的第k车辆f(m, k)的第一个配送点.

b) 配送点i是否为配送中心M的第k车辆f(m, k)的最后一个配送点.

c) 紧前配送点i是和紧后配送点j是否由配送中心M的第k车辆f(m, k)完成.

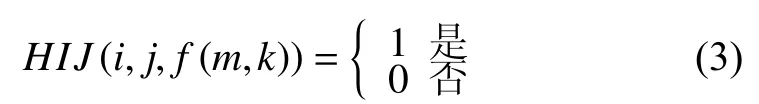
(4) 中间变量: 决策变量确定后, 即可计算出中间变量.

Sst(f(m, k), i)表示m中心的车辆k到达配送点i的实际时间:

SD(f(m, k))表示m中心车辆k行使的总路程:

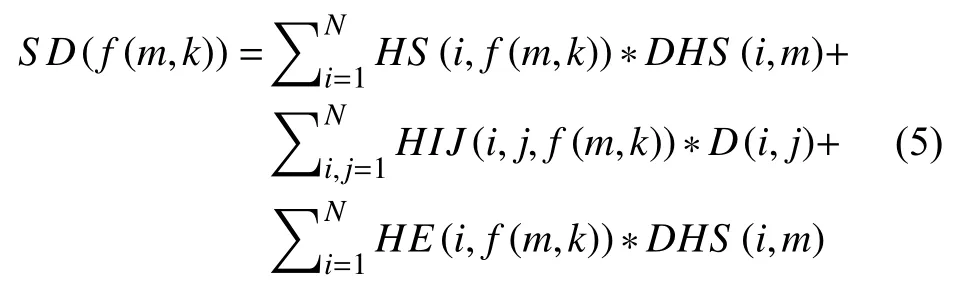
U(f(m, k))用于判别m中心的车辆k是否被调用:

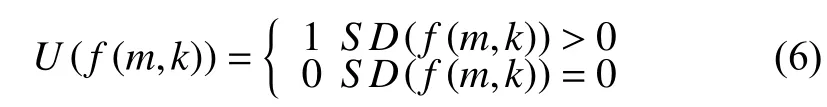
2.2 模型目标函数的确定

首先分析动用车辆的固定成本, 固定成本主要包括人力成本(驾驶员和装卸工)、车辆管理成本和折旧成本等. VFC表示完成整个物流订单所有物流中心动用车辆的固定成本:

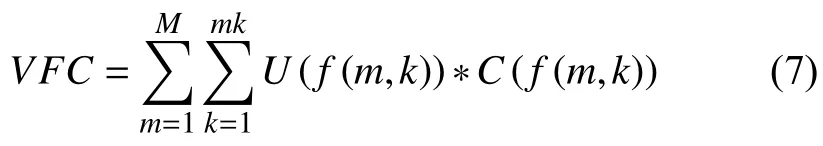
其次分析货物配送的运输成本, 运输成本主要包括车辆的燃油费、路桥费用等, 其中SD(f(m, k))表示m中心第k辆车的行驶距离, UC(f(m, k))表示该辆车单位行使距离的消耗成本. VTC表示总的运输成本:

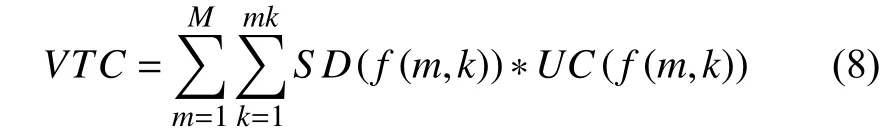
模型的目标函数为总成本SUMC=VFC+VTC最小.

约束条件:

(1) 任一配送点i, 只能由一辆车完成配送. 由2.1中的(3)节内容看出, 任一配送点i只能由某配送中心m第k辆车完成, 如为车辆的第一个配送点时, 决策变量HS(i, f(m, k))=1; 如为车辆的最后一个配送点时, 决策变量HE(i, f(m, k))=1; 否则为中间节点, 只能为某一个节点j的紧前节点, 因此

(2) 每个客户服务时间必须在约束的时间窗内.lt(i)和ut(i)为配送节点i所要求的货物到达的最早时间和最迟时间, Sst(f(m, k), i)为车辆实际达到节点i的时间点.

(3) 保证配送中心的车辆经过一系列的配送任务最终回到原点. 对任一车辆k, 如其承担某配送点i为出发点时, 必有另一配送点j为其最终配送点, 完成最终配送任务后, 返回配送中心.

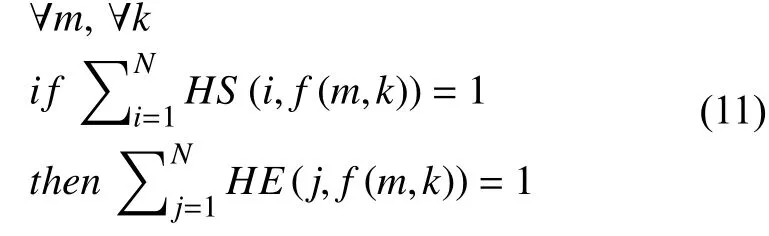
(4) 对于m中心任一车辆k, 其负责的配送点的需求货物总重量之和不能超出车辆k的最大载重量g(f(m,k)).

(5) 假如配送点i和配送点j由同车配送, 货物类别差级应不大于L, 即同车货物类别不冲突, 例如食物和农药、或带刺激性的气味货物不能同车, L的取值取决于货物具体的编码方案.

3 基于聚类分析的海量订单共同配送调度模型求解

在实际的配送过程中, 考虑到车辆的载重限制、行驶距离最小、返回原配送中心等约束条件, 可以断定配送车辆负责完成的配送点必将分布配送的周围附近, 这就提示我们针对众多物流中心、海量订单的配送问题可以通过聚类划分成多个单中心的物流配送问题, 降低问题的求解规模, 然后启发式优化算法各个求解, 最后通过反复迭代聚类分析结合优化算法可求出全局最优解.

3.1 基于单亲遗传的单中心车辆调度问题求解

假设某城市均匀分布着m个物流中心, 要获取整个城市海量订单优化调度方案(多中心配送), 首先解决单中心车辆调度优化问题, 下面以单配送中心多配送点车辆调度问题为例, 采用单亲遗传算法求解进行说明.

定义1. 虚拟配送点, 形式类同于一般配送点, 其货物需求量为零, 与配送中心及其他配送点的距离为零,仅为染色体基因交叉而定义.

(1) 染色体编码采用整数编码, 染色体中基因由配送点编号、配送中心编号和虚拟配送点组成. 如图1所示, 图中的s为配送中心编号, v为虚拟配送点, 相邻两个s节点代表一辆车的运输路径.

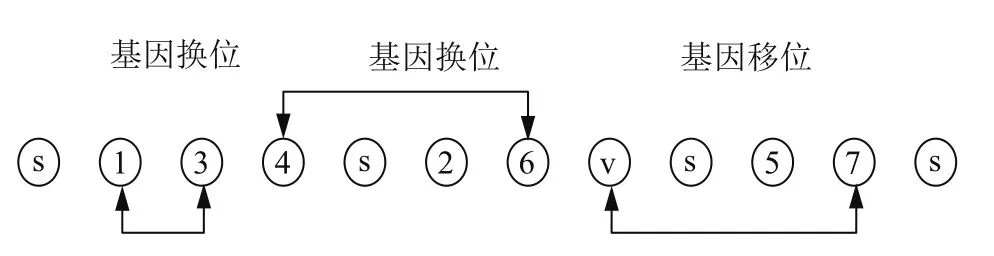
图1 染色体编码示意图

这个编码方案优点是染色体确定后, 很容易计算出决策变量HS(i, f(m, k))、HE(i, f(m, k))、HIJ(i, j, f(m,k)), 并根据公式(4)、(5)、(6)计算出中间变量Sst(f(m,k), i)和SD(f(m, k)).

(2) 初始染色体的生成, 针对类中的配送点, 可随机生成若干组染色体.

(3) 计算染色体中各基因的换位概率, 虚拟配送点的换位概率为1, 其他配送节点换位概率以配送节点3为例说明.

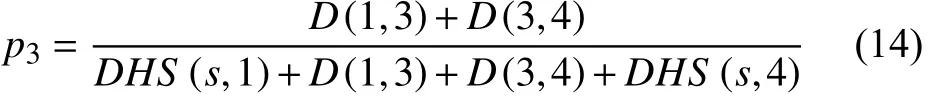
(4)针对种群中染色体, 随机产生两个换位节点及随机数p(0, 1), 如果两个节点的换位概率均大于p, 实施基因换位; 否则重新产生换位节点和随机数p.

(5)根据车辆时间窗约束条件公式(10)和载重约束条件(12)检查每条路径的可行性、, 剔出不满足约束条件的染色体.

(6)根据公式(7)和(8)计算配送中心总成本SUMC,包括车辆固定成本VFC和车辆运输成本VTC, 及m中心的总成本Z(m).

(7)如果连续几次最优总成本SUMC不再降低, 即获取最优解, 算法结束. 否则转(8).

(8)选择出种群中总成本SUMC最少的若干染色体最为新种群, 转步骤(3).

3.2 基于聚类分析的海量订单调度算法

配送中心的运输能力决定了它能够负责周围配送点的多少, 因此可根据配送中心的运输能力, 选择周围配送点的聚类半径, 结合蚁群算法[15]实施海量订单的优化调度. 具体算法如下:

(1) 初始化参数α, β, 准备N组蚂蚁, 每组m个蚂蚁随机分布于m个配送中心(聚类中心).

(2) 针对每个聚类中心i, 按照搜索半径r范围, 确定范围内的配送点Vi, 要求Vi的并集为所有需求点. 初始化蚂蚁的禁忌表Tubai=Vi, 令ηij=1/dhs(i, j), dhs(i, j)为配送点j到配送中心i的距离.

(3) 针对每只蚂蚁k, 随机选取搜索范围内的配送点j, 按照概率最大转移规则, 分配配送点j于配送中心i中, 令s(i, j)=1, 并将配送点j输入禁忌表Tubai.

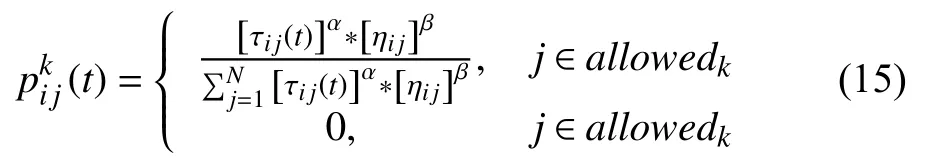
其中: τij(t)为t时刻, 配送点j到配送中心i路径的信息素.

(4) 当一组蚂蚁搜索完成后, 所有的配送点分配完毕, 按照3.1节的算法, 计算各配送中心的配送成本Z(m), 然后计算总成本SumC=∑Z(m).

(5) 记录蚂蚁k经过配送点j和配送中心i路径的信息增量.

(6) 当N组蚂蚁全部完成搜索, 转(7), 否则转(3).

(7) 更新蚂蚁分组配送点到配送中心路径上的信息量, 并记录最好的分类结果.

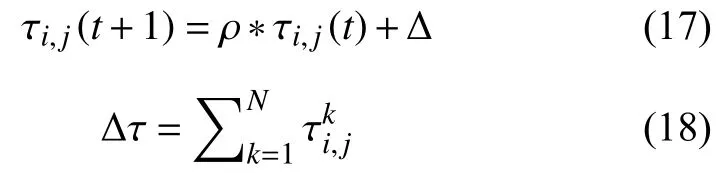
(8) 如连续几次SumC不再降低, 算法结束; 否则转(2), 直至总成本不再降低.

4 实验分析

云物流城市共同配送车辆调度问题优化研究过程中, 为了节省计算资源, 且更加清晰直观的说明所要研究的问题, 选取了37个配送点和6个配送中心作为研究对象, 针对配送点订单信息的三个属性进行聚类调度分析, 包括: 横坐标、纵坐标、订单类别(共包含十个等级, 不同等级代表不同种类的货物; 级别相差越大,种类差别越大, 本文假定相差2个级别, 不能同车装载),车辆行驶单公里成本1元. 假定这些订单和配送中心分布在100*100的区域内, 具体订单数据和配送中心信息如表1, 表2所示.

针对3.2节中的聚类算法, α=1.9反映了配送点被聚类到任一配送中心的历史信息强度, α过小, 历史信息重视不够, 算法收敛较慢; α过大, 容易陷入局部最优化.β=1.2表示启发式信息(配送点到配送中心的距离DHS)受重视的程度, 显然β过大, 聚类结果受距离DHS影响较大, 容易陷入局部最优. 共设置50组蚂蚁,每组蚂蚁数37只, 经过239次迭代获取调度方案如表3和图2所示.

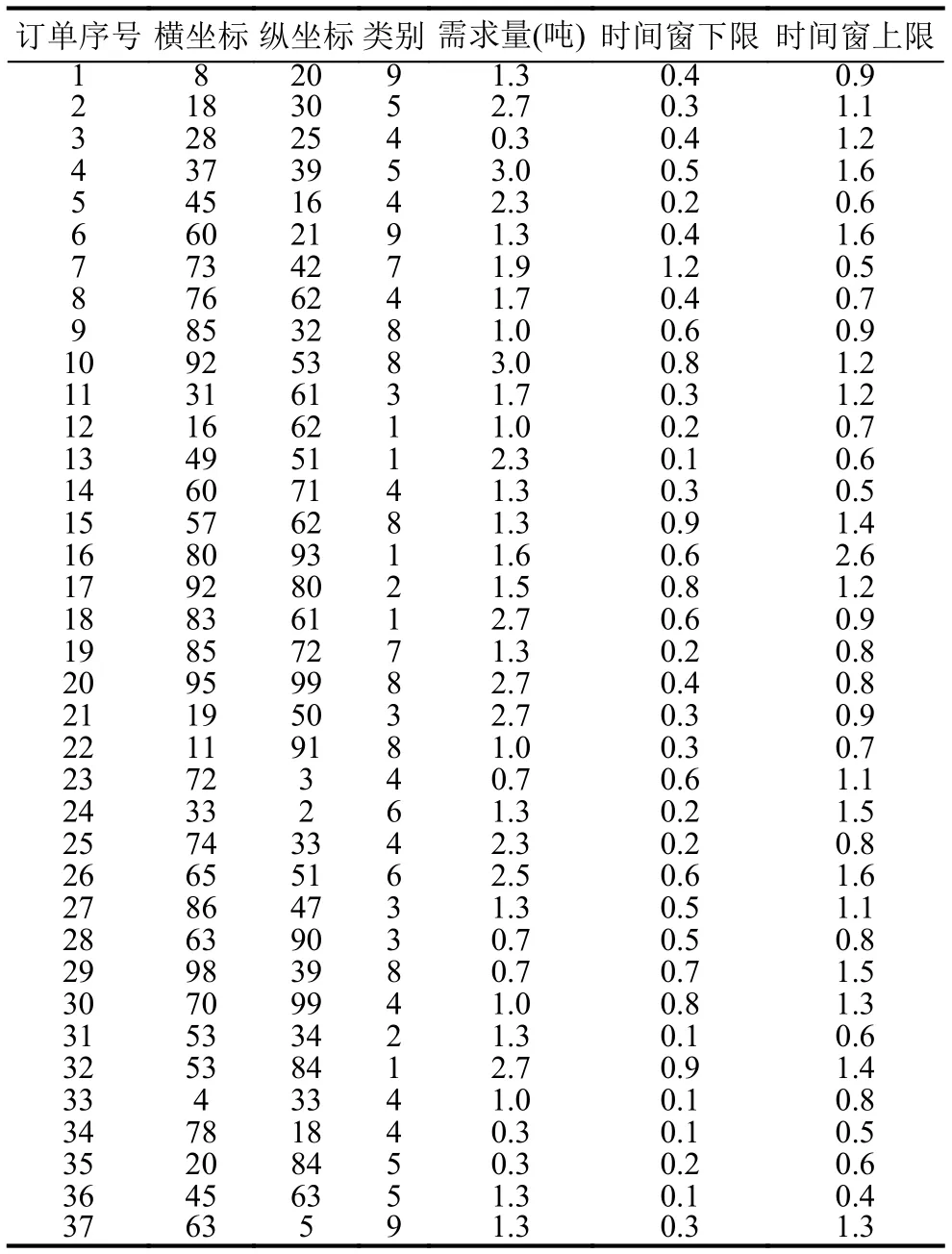
表1 订单信息表

表2 配送中心信息表

表3 车辆调度最优路径

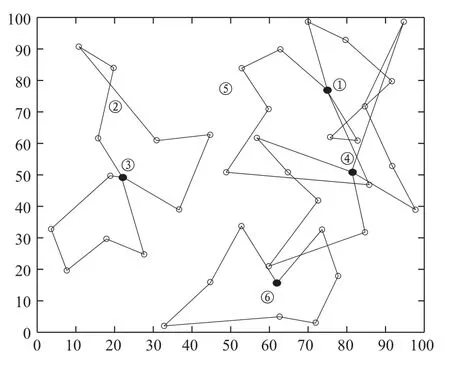
图2 聚类及车辆优化调度路线图

分析表3不难看出, 6个配送中心经聚类优化后, 选择其中四个参与配送任务. 配送中心1, 3和4各出2辆车,中心6出1辆车, 车辆行驶路径、配载率、行使距离见表3, 各车配载率较高, 均在75%以上.

如上所示, 图2展示了6个配送中心、37个配送点的空间位置、以及7辆车的负责配送的行驶路径. 配送中心②和⑤不参与配送任务. 经过实心点(配送中心①③④⑥)的封闭曲线为各车辆的行驶路线. 配送中心③和⑥负责的配送点不存在运送货物种类冲突问题,车辆路径基本符合路径最短原则, 配送中心①和④负责配送点存在物品类别冲突, 类别冲突的货物不能同车配送, 同时为了满足各配送点时间窗约束, 车辆路径出现交叉, 并未满足路径最短原则, 这与实际情况相符,并不影响总体配送成本降低.

5 结语

针对云物流环境下城市共同配送海量订难以调度问题, 本文提出基于订单聚类结合单中心多车辆优化调度的迭代算法, 对海量订单调度问题进行了探讨研究. 单中心多车辆调度模块由各中心服务器完成, 物流订单聚类分析由云物流中心系统已完成, 实现分布式调度, 以便快速求出车辆调度最优解.

1贡祥林, 杨蓉. “云计算”与“云物流”在物流中的应用. 中国流通经济, 2012, 26(10): 29–33. [doi: 10.3969/j.issn.1007-8266.2012.10.006]

2张水旺, 胡小建. 云物流概念模型及其运作机理研究. 科技管理研究, 2015, 35(19): 186–190, 196. [doi: 10.3969/j.issn.1000-7695.2015.19.035]

3田冉, 孙林夫, 唐慧佳, 等. 多车场物流协同运输调度问题研究. 计算机工程与应用, 2015, 51(21): 230–236. [doi:10.3778/j.issn.1002-8331.1408-0158]

4王天成. 物流配送车辆优化调度问题概述. 物流工程与管理, 2013, 35(8): 29–30.

5杭省策, 李怀祖. 多车场车流分配的广义指派模型及其分解算法. 西安交通大学学报, 1997, (12): 111–116.

6郭耀煌, 李军. 车辆优化调度问题的研究现状评述. 西南交通大学学报, 1995, 30(4): 376–382.

7张明善, 唐小我. 多车场满载货运车辆优化调度的网络流算法. 系统工程学报, 2002, 17(3): 216–220.

8Bianchessi N, Righini G. Heuristic algorithms for the vehicle routing problem with simultaneous pick-up and delivery.Computers & Operations Research, 2007, 34(2): 578–594.

9李作秋, 王国林. 一种有时间窗约束的非满载车辆调度问题中的启发式算法研究 .公路交通科技 ,2006 ,23(7) :147–149.

10Golden BL, Raghavan S, Wasil EA. The Vehicle Routing Problem: Latest Advances and New Challenges. US:Springer, 2008.

11马宇红, 姚婷婷, 张芳芳. 多车场多车型车辆调度问题及其遗传算法. 数学的实践与认识, 2014, 44(2): 107–114.

12王骏, 王士同, 邓赵红. 聚类分析研究中的若干问题. 控制与决策, 2012, 27(3): 321–328.

13张建强, 方卫国. 有时间窗约束车辆路径问题的改进遗传算法. 计算机工程与应用, 2010, 46(32): 228–231. [doi:10.3778/j.issn.1002-8331.2010.32.063]

Research on Massive Orders Scheduling Problem of Urban Joint Distribution Based on Clustering

XIE Tian-Bao1, ZHAO Meng1, LEI Xi-Ling2

1(School of Economics and Management, Xi’an University of Technology, Xi’an 710054, China)
2(School of Computer Science and Engineering, Xi’an University of Technology, Xi’an 710054, China)

In order to solve the problem of massive orders scheduling in the cloud logistics environment, this paper proposes a scheduling algorithm based on orders clustering. Firstly, aiming at the single center multi vehicle scheduling problem, an optimal scheduling algorithm based on the single parent genetic algorithm is proposed. On this foundation,considering the location of the city distribution centers, the vehicles and the distribution points, the type and the demand of goods, an order clustering model based on distribution center is built by using the ant colony algorithm.

joint distribution; massive orders; clustering; ant colony algorithm; scheduling

谢天保,赵萌,雷西玲.基于聚类的城市共同配送海量订单调度问题研究.计算机系统应用,2017,26(7):232–237. http://www.c-sa.org.cn/1003-3254/5837.html

陕西省教育厅人文社科重点研究基地科研计划项目(15JZ039)

2016-10-28; 收到修改稿时间: 2016-11-30