FINITE GROUPS WHOSE ALL MAXIMAL SUBGROUPS ARE SMSN-GROUPS

GUO Peng-fei

(1.School of Mathematics and Statistics,Hainan Normal University,Haikou 571158,China)(2.School of Mathematics and Information Engneering,Lianyungang Normal College,Lianyungang 222006,China)

FINITE GROUPS WHOSE ALL MAXIMAL SUBGROUPS ARE SMSN-GROUPS

GUO Peng-fei1,2

(1.School of Mathematics and Statistics,Hainan Normal University,Haikou 571158,China)(2.School of Mathematics and Information Engneering,Lianyungang Normal College,Lianyungang 222006,China)

A fi nite groupGis called an SMSN-group if its 2-maximal subgroups are subnormal inG.In this paper,the author investigates the structure of fi nite groups which are not SMSN-groups but all their proper subgroups are SMSN-groups.Using the idea of local analysis,a complete classi fi cation of this kind of groups is given,which generalizes some results of the structure of fi nite groups.

power automorphisms;nilpotent groups;minimal non-nilpotent groups;minimal non-SMSN-groups

1 Introduction

All groups in this paper are fi nite and our notation is standard(see[1]).Let Σ be an abstract group theoretical property,for example,nilpotency,supersolvability,solvability,etc.If all proper subgroups of a groupGhave the property Σ butGdoes not have the property Σ,thenGis called a minimal non-Σ-group.

One of the hottest topics in group theory is to determinate the structure of minimal non-Σ-groups and many meaningful results about this topic were obtained.The speci fi c papers about this topic can refer to[2-10].

The aim of this paper is to study the structure of a kind of minimal non-Σ-groups.We call the groups whose 2-maximal subgroups are subnormal SMSN-groups.A groupGis a minimal non-SMSN-group if every proper subgroup ofGis an SMSN-group butGitself is not,and we classify the minimal non-SMSN-groups completely.

2 Preliminaries

In this section,we give some de fi nitions and some lemmas needed in this paper.

Lemma 2.1(see[5,Lemma 5])Every 2-maximal subgroup of a groupGis subnormal if and only if eitherGis nilpotent orGis a Schmidt group with abelian Sylow subgroups.

Lemma 2.2IfGis a solvable minimal non-SMSN-group,then|π(G)|≤3.

ProofIf|π(G)|≥ 4,then every maximal subgroup ofGhas at least three prime divisors sinceGis solvable.Applying Lemma 2.1,Gis minimal non-nilpotent,a contradiction.Hence|π(G)|≤3.

Lemma 2.3(see[10]) Any minimal simple group(non-abelian simple group all of whose proper subgroups are solvable)is isomorphic to one of the following simple groups

(1)PSL(3,3);

(2)PSL(2,p),wherepis a prime withp＞3 and

(3)PSL(2,2q),whereqis a prime;

(4)PSL(2,3q),whereqis an odd prime;

(5)The Suzuki group Sz(2q),whereqis an odd prime.

Lemma 2.4(see[11])Suppose thatp′-groupHacts on ap-groupG.Let

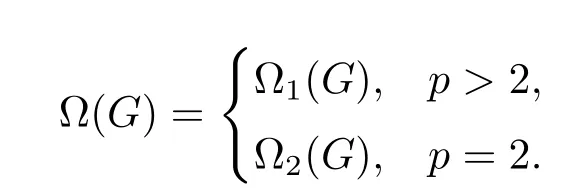
IfHacts trivially on Ω(G),thenHacts trivially onGas well.

Lemma 2.5(see[7,Lemma 2.9])If ap-groupGof orderpn+1has a unique non-cyclic maximal subgroup,thenGis isomorphic to one of the following groups

(I)Cpn×Cp=〈a,b|apn=bp=1,[a,b]=1〉,wheren≥ 2;

(II)Mpn+1=〈a,b|apn=bp=1,b-1ab=a1+pn-1〉,wheren≥ 2 andn≥ 3 ifp=2.

Lemma 2.6(see[12])LetGbe a group andHa nilpotent subnormal subgroup ofG.ThenGcontains a nilpotent normal subgroup ofGcontainingH.

3 Main Results

In this section,we give the speci fi c classi fi cation of the minimal non-SMSN-groups.

Theorem 3.1A non-solvable groupGis a minimal non-SMSN-group if and only ifGis isomorphic toA5,whereA5is the alternating group of degree 5.

ProofWe only prove the necessity part.

SinceGis a non-solvable group whose maximal subgroups are all SMSN-groups,thenGis a minimal non-solvable group by Lemma 2.1,and soG/Φ(G)is a minimal simple group.

Case 1Assume Φ(G)=1.ThenGis isomorphic to one of the simple groups mentioned in Lemma 2.3.

LetPSL(2,2q).By[14,Corollary 2.2],Ghas maximal subgroups：the dihedral groups of order 2(2q±1);the Frobenius groupHof order 2q(2q-1);the alternating groupA4of degree 4 whenq=2.Clearly,5whenq=2 and it is a minimal non-SMSN-group.Ifq＞2,then 3| 2q+1.It follows from Lemma 2.1 thatGis not a minimal non-SMSN-group.

LetPSL(2,3q).Similar arguments as above,Ghas a dihedral groupBwhose Sylow 2-subgroups are neither cyclic nor normal,which contradicts the fact thatBis an SMSN-group.SoGPSL(2,3q).

LetGSz(2q).By[15,Theorem 9],Ghas a Frobenius groupKof orderbut the Sylow 2-subgroups ofKare neither cyclic nor normal,a contradiction.SoG?Sz(2q).

Case 2Assume Φ(G)1.It is easy to see that(G/Φ(G))=1 andG/(G)is a non-solvable minimal non-SMSN-group.Similar arguments as above and by induction,G/(G)5.HenceGhas two non-nilpotent maximal subgroupsM1andM2such thatM1/(G)4andM2/Φ(G)10,whereA4is the alternating group of degree 4 andD10is the dihedral group of order 10.SinceM1andM2are SMSN-groups,they are minimal non-nilpotent by Lemma 2.1.It makes|G|=2a·3·5 and|(G)| =2a-2,wherea≥ 3.By Lemma 2.1 again,the Sylow 2-subgroups ofM1are elementary abelian.At the same time,the Sylow 2-subgroups ofM2are cyclic whose orders are more than 2 by Lemma 2.1,a contradiction.

Theorem 3.2The minimal non-SMSN-groupGwhose order has exactly two prime divisorspandqis exactly one of the following types(PandQare Sylow subgroups)

(1)G=〈x,y|xp=yqn=1,y-1xy=xi〉,whereiq/1(modp),iq2≡ 1(modp),p＞q,n≥2 and 0＜i＜p;

(2)G=〈x,y|xpq=yq=1,y-1xy=xi〉,wherep≡ 1(modq),i≡ 1(modq),iq≡1(modp)and 1＜i＜p;

(3)G=〈x,y|x4p=1,y2=x2p,y-1xy=x-1〉;

(4)G=〈x,y,z|xp=yqn-1=zq=1,y-1xy=xi,[x,z]=1,[y,z]=1〉wherep＞q,1(modp),iq≡1(modp)andn≥3;

(5)G=〈x,y,z|xp=yqn-1=zq=1,y-1xy=xi,[x,z]=1,z-1yz=y1+qn-2〉,wherep＞q,1(modp),iq≡1(modp),n≥3 andn≥4 ifq=2;

(6)G=PQ,whereP=〈a1〉×〈a2〉×···×〈ar〉is an elementary abelianp-group withr≥ 2,Q=〈y〉with|y|=qnandn≥ 2,〈yq〉acts irreducibly onPand〈yq2〉centralizesP;

(7)G=PQ,whereP=〈a1〉×〈a2〉×···×〈ar〉is an elementary abelianp-group andr≥ 2,Q=〈y〉with|y|=qnandn≥ 1,[a1,Q]=1,Qacts irreducibly on〈a2〉×···×〈ar〉and Φ(Q)centralizesP;

(8)G=PQ,whereP=〈a1〉×〈a2〉×···×〈ar〉is an elementary abelianp-group withr≥ 2,Q=〈y〉with|y|=qnandn≥ 1,Qacts irreducibly on〈a1〉×···×〈al-1〉and〈al〉×···×〈ar〉withl≥2,and Φ(Q)centralizesP;

(9)G=PQ,whereP=〈a1〉×〈a2〉×···×〈ar〉(r≥ 2)is ap-group with|a1| =|a2| =···=|ar| =p2,Q=〈y〉with|y|=qnandn≥ 1,Qacts irreducibly on Φ(P),Φ(Q)centralizesP,andG/Φ(P)is a minimal non-abelian group;

(10)G=PQ,wherePis a non-abelian specialp-group of rank 2m,the order ofpmoduloqbeing 2m,Q=〈y〉is cyclic of orderqr＞1,yinduces an automorphism inPsuch thatP/Φ(P)is a faithful and irreducibleQ-module,andycentralizes Φ(P).Furthermore,|P/Φ(P)| =p2mand|P′|≤pm;

(11)G=PQ,wherePis a non-abelian specialp-group with exp(P)≤p2and| Φ(P)|≥p2,Q=〈y〉with|y|=qnandn≥ 1,Qacts irreducibly on Φ(P),Φ(Q)centralizesP,andG/Φ(P)is a minimal non-abelian group;

(12)G=PQ,whereP=〈a1〉×〈a2〉×···×〈ar〉is an elementary abelianp-group withr≥ 2,Q=〈a,b|aq=bq=1,[a,b]=1〉,[P,b]=1,〈a〉acts irreducibly onP;

(13)G=PQ,whereP=〈a1〉×〈a2〉×···×〈ar〉is an elementary abelianp-group withr≥ 2,Q=〈a,b|aq=bq=1,[a,b]=1〉,〈a〉and〈b〉act irreducibly onP;

(14)G=PQ,whereP=〈a1〉×〈a2〉×···×〈ar〉is an elementary abelianp-group withr≥ 2,Q=〈a,b|a4=1,b2=a2,b-1ab=a-1〉,[P,b]=1 and〈a〉acts irreducibly onP;

(15)G=PQ,whereP=〈a1〉×〈a2〉×···×〈ar〉is an elementary abelianp-group withr≥ 2,Q=〈a,b|a4=1,b2=a2,b-1ab=a-1〉,[P,a2]=1,〈a〉and〈b〉act irreducibly onP;

(16)G=PQ,whereP=〈a1〉×〈a2〉×···×〈ar〉is an elementary abelianp-group withr≥2,Q=〈y,z|yqn-1=zq=1,[y,z]=1〉withn≥ 3,z∈Z(G),〈y〉acts irreducibly onPand〈yq〉centralizesP;

(17)G=PQ,whereP=〈a1〉×〈a2〉×···×〈ar〉is an elementary abelianp-group withr≥2,Q=〈y,z|yqn-1=zq=1,z-1yz=y1+qn-2〉withn≥ 3 andn≥ 4 ifq=2,〈z〉≤CG(P),〈y〉acts irreducibly onPand〈yq〉centralizesP;

(18)G=PQ,whereP=〈x〉Gwith|P|=p,Q=(〈a1〉×〈a2〉×···×〈ar-1〉)〈ar〉is a non-normalq-group with3,F(G)=Oq(G)=〈a1〉×〈a2〉×···×〈ar-1〉,Pacts irreducibly onOq(G),a-1rxar=xiandp＞q,whereiis a primitiveq-th root of unity modulop,F(G)is the Fitting subgroup ofG.

ProofIfGis a solvable minimal non-SMSN-group whose order has exactly two prime divisors,then we assumeG=PQ,whereP∈Sylp(G)andQ∈Sylq(G).

Assume thatPandQare neither cyclic nor normal inG.The solvability ofGimplies thatGhas a normal subgroupMof prime index,sayq.LetMpbe a Sylowp-subgroup ofM.SinceMis an SMSN-group,we have thatMpis either cyclic or normal inMby Lemma2.1.ClearlyMpmust be normal inMsince it is also a Sylowp-group ofG.Now it follows fromMpcharMGthatMpG,a contradiction.SoGhas a Sylow subgroup which is either cyclic or normal.

(1)Assume thatPandQare cyclic and letP=〈x〉andQ=〈y〉with|x|=pm,|y|=qnandp＞q.In this case,y-1xy=xiwithiqn≡1(modpm),0＜i＜pmand(pm,qn(i-1))=1.Considering the maximal subgroupsP〈yq〉and〈xp〉QofG,if〈xp〉Q=〈xp〉×Q,then by Lemma 2.4,Gis nilpotent,a contradiction.This implies〈xp〉Q=〈xp〉Q.By Lemma 2.1,xp=1,〈yq〉is not normal inG,but〈yq2〉is normal inG.Soiq1(modp),iq2≡ 1(modp)andGis of type(1).

(2)Assume thatPis a cyclic normal subgroup ofGandQis neither cyclic nor normal inG.Ifq＞p,then by Burnside’s theorem[1,10.1.8],QG,a contradiction.Soq＜p.IfQhas two non-cyclic maximal subgroupsQ1andQ2,then by Lemma 2.1,PQ1=P×Q1,PQ2=P×Q2and soQ=Q1Q2is normal inG,a contradiction.Therefore,every maximal subgroup ofQis cyclic orQhas a unique non-cyclic maximal subgroup,and soQis an elementary abelianq-group of orderq2,the quaternion groupQ8or one of the types in Lemma 2.5.

Case 1AssumeP=〈z〉andQ=〈a,b|aq=bq=1,[a,b]=1〉.If〈a〉and〈b〉acting onPby conjugation are both trivial,thenGis nilpotent,a contradiction.Therefore,we may assume that〈a〉acting onPby conjugation is non-trivial.By Lemma 2.1,zp=1.IfCG(P)=P,thenG/CG(P)is an elementary abelianq-group of orderq2.However,G/CG(P)Aut(P),and Aut(P)is cyclic,a contradiction.Hencebis contained inCG(P).Clearly,CG(P)=〈x〉,y-1xy=xi,|x|=pq,y=a,q|p-1,i≡1(modq)andiq≡ 1(modp),wherex=zbis a generator ofCG(P).SoGis of type(2).

Case 2AssumeP=〈z〉andQ=Q8=〈a,b|a4=1,b2=a2,b-1ab=a-1〉.Similar arguments as Case 1,we have thatzp=1,bis contained inCG(P)and|Z(G)| =2.SoCG(P)=〈x〉with|x|=4p,y=a,y-1xy=xiandi2≡ 1(mod 4p),wherex=zbis a generator ofCG(P).By computations,Gis of type(3).

Case 3Assume thatP=〈x〉andQis the type of Lemma 2.5(I)with|Q|=qn.Namely,Q=〈y,z|yqn-1=zq=1,[y,z]=1〉,wheren≥ 3.ThenQhas maximal subgroupsH=〈y〉,K0=〈yq,z〉andKs=〈yq,zys〉=〈zys〉withs=1,···,q-1,whereK0is the unique noncyclic maximal subgroup ofQ.By hypothesis and Lemma 2.1,,PK0=P×K0andxp=1.HenceG=〈x,y,z|xp=yqn-1=zq=1,y-1xy=xi,[x,z]=1,[y,z]=1〉,where1(modp),iq≡1(modp).SoGis of type(4).

Case 4 Assume thatP=〈x〉andQis the type of Lemma 2.5(II)with|Q|=qn.Namely,Q=〈y,z|yqn-1=zq=1,z-1yz=y1+qn-2〉,wheren≥ 3 andn≥ 4 ifq=2.In the similar way as above,we have thatxp=1,〈z〉≤CG(P)andy-1xy=xi,where1(modp)andiq≡ 1(modp).SoGis of type(5).

(3)Assume thatPis a non-cyclic normal subgroup ofGandQ=〈y〉is non-normal cyclic subgroup ofGwith|y|=qn.If there exists a subgroupP∗ofPwith 1＜Φ(P)＜P∗＜Psuch thatP∗Q=QP∗,thenP∗GsinceP∗is subnormal inG.By Maschke’s theorem[1,8.1.2],Phas a subgroupKwith 1＜K＜Psuch thatP/Φ(P)=P∗/Φ(P)×K/Φ(P),KG,,and at least one ofP∗QandKQis a non-nilpotent SMSN-group.By Lemma 2.1,it is easy to see thatP∗∩K= Φ(P)=1,a contradiction.Hence Φ(P)=1 orP/Φ(P)is the minimal normal subgroup ofG/Φ(P)when Φ(P)/1.

Case 1Assume Φ(P)=1.IfPis a minimal normal subgroup ofG,then by hypothesis,the maximal subgroupPΦ(Q)ofGis non-nilpotent.By Lemma 2.1,〈yq〉acts irreducibly onPand[P,yq2]=1.SoGis of type(6).IfPhas a non-trivial proper subgroupP1which is normal inG,then there exists a subgroupP2ofPsuch thatP=P1×P2andP2Gby Maschke’s theorem[1,8.1.2].Clearly,at least one action that〈y〉acts onP1andP2by conjugation is non-trivial.IfP1Q=P1×QandP2Q=P2Q,then by Maschke’s theorem[1,8.1.2]and Lemma 2.1,it is easy to see that|P1| =p,[P,yq]=1 andGis of type(7).IfP1Q=P1QandP2Q=P2Q,then by Lemma 2.1,〈y〉acts irreducibly onP1andP2,and[P,yq]=1.SoGis of type(8).

Case 2Assume Φ(P)＞1 andZ(P)=P.By the same arguments as the beginning of(3),it is easy to see that Φ(P)is the unique normal subgroup ofGwhich is contained inP,and soPis a homocyclicp-group(a product of some cyclic subgroups of the same order).By Lemma 2.1 and Lemma 2.4,we have easily that the exponent ofPisp2,one maximal subgroupPΦ(Q)ofGis nilpotent.Hence another maximal subgroup Φ(P)Qis non-nilpotent,and〈y〉acts irreducibly on Φ(P).Clearly the quotient groupG/Φ(P)is a minimal non-abelian group.SoGis of type(9).

Case 3Assume Φ(P)＞1 andZ(P)＜P.Similarly,Φ(P)=Z(P)=P′is the unique non-trivial characteristic subgroup ofP,that is,Pis a specialp-group with exp(P)≤p2andPΦ(Q)is nilpotent.If Φ(P)Qis nilpotent also,then by a result in[4,Theorem 2],Gis of type(10).If| Φ(P)| =pandp＜q,thenGbelongs to type(10).If Φ(P)Qis non-nilpotent with| Φ(P)| =pandp＞q,thenGis minimal non-supersolvable.Examining a result in[4,Theorem 10],Gis not isomorphic to anyone of them.If Φ(P)Qis non-nilpotent with| Φ(P)|≥p2,then the quotient groupG/Φ(P)is a minimal non-abelian group.SoGis of type(11).

(4)Assume thatPis a non-cyclic normal subgroup ofGandQis neither cyclic nor normal inG.If Φ(P)＞1,then by Lemma 2.1,PQ1andPQ2are both nilpotent and soGis nilpotent,a contradiction,whereQ1andQ2are two distinct maximal subgroups ofQ.HencePis an elementary abelianp-group of orderprwithr≥2.Similar arguments as in(2),Qis an elementary abelianq-group of orderq2,the quaternion groupQ8or one of the types in Lemma 2.5.

Case 1LetQ=〈a,b|aq=bq=1,[a,b]=1〉.Clearly,there exists a non-trivial automorphism that〈a〉or〈b〉acts onPby conjugation.We may assume that〈a〉acting onPby conjugation is non-trivial and〈b〉acting onPby conjugation is trivial.SoGis of type(12).If〈a〉and〈b〉acting onPby conjugation are both non-trivial,thenGis of type(13).

Case 2LetQ=Q8=〈a,b|a4=1,b2=a2,b-1ab=a-1〉.Similar arguments as above,Gis of either type(14)or type(15).

Case 3LetQbe as in Lemma 2.5(I)with|Q|=qn.Namely,Q=〈y,z|yqn-1=zq=1,[y,z]=1〉,wheren≥ 3.Similar arguments as Case 3 in(2),〈y〉acts irreducibly onP,[P,yq]=1 andz∈Z(G).SoGis of type(16).

Case 4LetQbe as in Lemma 2.5(II)with|Q|=qn.Namely,Q=〈y,z|yqn-1=zq=1,z-1yz=y1+pn-2〉,wheren≥ 3 andn≥ 4 ifp=2.Similar arguments as Case 4 in(2),〈y〉acts irreducibly onP,[P,yq]=1 and〈z〉≤CG(P).SoGis of type(17).

(5)Assume thatP=〈x〉is a non-normal cyclic subgroup ofGandQis neither cyclic nor normal inG.Clearlyp＞q.The solvability ofGimplies thatGhas a normal subgroupMof prime index.If|G：M|=p,then it is easy to see thatGhas a normal Sylowq-group sinceMis an SMSN-group and applying Lemma 2.1,a contradiction.Therefore,|G：M|=q.If there exists a cyclic Sylowq-subgroupMqofM,thenMhas a normal Sylowp-subgroupMp,and soMpis a normal Sylowp-subgroup ofG,a contradiction.HenceMqis non-cyclic and|Q|≥q3.By Lemma 2.1,Mqis normal inMandMphas a maximal subgroupP1such thatP1is normal inM,whereMpis a Sylowp-subgroup ofM.HenceMqandP1are both subnormal inG.By Lemma 2.6,F(G)=P1×Mq=Op(G)×Oq(G).Clearly,Op(G)=〈xp〉andOq(G)=〈a1〉×〈a2〉×···×〈ar-1〉is an elementary abelianqgroup with|Oq(G)|≥q2.IfNG(P)is nilpotent,thenNG(P)=CG(P)sincePis cyclic.By Burnside Theorem[1,10.1.8],Gisp-nilpotent,a contradiction.HenceNG(P)=P〈ar〉is a Schmidt subgroup ofG,and soP〈aqr〉is nilpotent with|P|=pby Lemma 2.1,wherearis aq-element.SinceMis a Schmidt subgroup ofGalso,Oq(G)is a minimal normal subgroup ofGandG=MNG(P).HenceOq(G)〈ar〉is a Sylowq-subgroup ofGandFurthermore,|ar| =qsinceOq(G)Pis a Schmidt subgroup ofG.If Φ(Q)=1,thenQis abelian.HenceNG(Q)=CG(Q)=QG.SoGisq-nilpotent,a contradiction.If Φ(Q)1,thenQ=(〈a1〉×〈a2〉×···×〈ar-1〉)〈ar〉.SoGis of type(18).

Conversely,it is clear that the groups of types(1)-(18)are minimal non-SMSN-groups.

Theorem 3.3The solvable minimal non-SMSN-groupGwhose order has exactly three prime divisorsp,qandris exactly one of the following types(P,QandRare Sylow subgroups)

(1)G=(P×Q)oR,where[P,R]=1,|P|=p,Qis an elementary abelianq-group,R=〈a〉is cyclic,Racts irreducibly onQand〈ar〉centralizesQ;

(2)G=(P×Q)oR,wherePandQare both elementary abelian,R=〈a〉is cyclic,Racts irreducibly onPandQ,〈ar〉centralizesPQ;

(3)G=P(Q×R),wherePis an elementary abelianp-group,Qis a group of orderq,Ris a group of orderr,QandRact irreducibly onP,respectively.

ProofIt is easy to see thatGhas at least one normal Sylow subgroup and we assume thatG=PQR,whereP∈Sylp(G),Q∈Sylq(G),R∈Sylr(G),andPG,RG.Clearly,we only need consider the following cases.

Case 1 IfQG,PR=P×RandQR=QR,thenQRis an SMSN-group.By Lemma 2.1,Qis an elementary abelianq-group andR=〈a〉is cyclic.If|,thenP1QRis nilpotent by Lemma 2.1 again,a contradiction,where 1＜P1＜P.Hence|P|=pandGis of type(1).

Similarly,ifQG,PR=PRandQR=Q×R,thenGis isomorphic to type(1)also.IfQG,PR=PRandQR=QR,it is easy to see thatGis of type(2).

Case 2IfQG,PQ=PQ,PR=P×R,QR=QR,then by Lemma 2.1,Pis an elementary abelianp-group,Q=〈a〉is a cyclic group of orderq,q＞randR=〈b〉is cyclic.SinceCG(P)=P×RNG(P)=G,RG,a contradiction.

IfQG,PQ=PQ,PR=PR,QR=Q×R,and Φ(R)1,thenPQΦ(R)is nilpotent by Lemma 2.1,a contradiction.Hence Φ(R)=1,thenGis of type(3).

Similarly,ifQG,PQ=PQ,PR=PR,QR=QR,thenPis elementary abelian,Q=〈a〉is a group of orderq,R=〈b〉is a group of orderrandr|q-1.Let|P|=pα,α≥ 1.Then by[16,Theorem 1.5],pα≡ 1(modq),pα≡ 1(modr).Hencepα-1=qm=rn,wheremandnare integers.Soq=rnm-1,a contradiction.

Conversely,it is clear that the groups of types(1)-(3)are minimal non-SMSN-groups.

By Lemma 2.1,combining Theorem 3.1,Theorem 3.2 and Theorem 3.3,the complete classi fi cation of the minimal non-SMSN-groups is as follows.

Corollary 3.4The minimal non-SMSN-groups are exactly the groups ofA5,types(1)to(18)of Theorem 3.2 and types(1)to(3)of Theorem 3.3,whereA5is the alternating group of degree 5.

[1]Robinson D J S.A course in the theory of groups[M].New York,Heidelberg,Berlin：Springer-Verlag,1980.

[4]Ballester-Bolinches A,Esteban-Romero R.On minimal non-supersoluble groups[J].Rev.Mat.Iberoamericana,2007,23(1)：127-142.

[5]Lutsenko1 Y V,Skiba A N.Finite groups with subnormal second or third maximal subgroups[J].Math.Notes.,2012,91(5)：680-688.

[6]Guo Wenbin,Legchekova E V,Skiba A N.Finite groups in which every 3-maximal subgroup commutes with all maximal subgroups[J].Math.Notes,2009,86(3)：325-332.

[7]Guo Pengfei,Guo Xiuyun.On minimal non-MSN-groups[J].Front.Math.China,2011,6(5)：847-854.

[8]Ma Lijie,Huang Benwen.Structure of a kind of groups of orderpnm[J].J.Math.,2010,30(4)：671-674(in Chinese).

[9]Qian Guohua.Finite groups to be able written as the union of four proper subgroups[J].J.Math.,2011,31(5)：891-892(in Chinese).

[10]Thompson J G.Nonsolvable fi nite groups all of whose local subgroups are solvable[J].Bull.Amer.Math.Soc.,1968,74：383-437.

[11]La ff ey T J.A Lemma on fi nitep-group and some consequences[J].Math.Proc.Cambridge Phil.Soc.,1974,75(2)：133-137.

[13]Conway J H,Curtis R T,Norton S P,Parker R A,Wilson R A.Atlas of fi nite groups[M].Oxford：Oxford University Press,1985.

[14]King O H.The subgroup structure of fi nite classical groups in terms of geometric con fi gurations[C].Surveys in Combinatorics,London Math.Soc.,Lecture Note,2005,327：29-56.

[15]Suzuki M.On a class of doubly transitive groups[J].Ann.Math.,1962,75(1)：105-145.

[16]Chen Zhongmu.Inner and outer-∑ groups and mininmal non-∑ groups[M].Chongqing：Southwest Normal University Press,1988(in Chinese).

所有极大子群都为SMSN-群的有限群

郭鹏飞1,2

(1.海南师范大学数学与统计学院,海南海口 571158)

(2.连云港师范高等专科学校数学与信息工程学院,江苏连云港 222006)

若有限群G的每个2-极大子群在G中次正规,则称G为SMSN-群.本文研究了有限群G的每个真子群是SMSN-群但G本身不是SMSN-群的结构,利用局部分析的方法,获得了这类群的完整分类,推广了有限群结构理论的一些成果.

幂自同构;幂零群;内幂零群;极小非SMSN-群

��20D10;20E34

O152.1

on：20D10;20E34

A Article ID： 0255-7797(2017)04-0714-09

date：2015-09-06Accepted date：2015-12-03

Supported by National Natural Science Foundation of China(11661031);Jiangsu Overseas Research&Training Program for University Prominent Young&Middle-Aged Teachers and Presidents;“333” Project of Jiangsu Province(BRA2015137);“521” Project of Lianyungang City.

Biography：Guo Pengfei(1972-),male,born at Wuxiang,Shanxi,professor,major in fi nite group theory.