态R0代数

秦玉静,辛小龙,贺鹏飞

(1.西北大学数学学院,陕西西安710127)

(2.陕西师范大学数学与信息科学学院,陕西西安710119)

态R0代数

秦玉静1,辛小龙1,贺鹏飞2

(1.西北大学数学学院,陕西西安710127)

(2.陕西师范大学数学与信息科学学院,陕西西安710119)

本文研究了R0代数上有关态算子的问题.利用MV-代数上内态的引入方法引入了态算子,定义了态R0代数,它是R0代数的一般化.给出了一些非平凡态R0代数的例子并讨论了态R0代数的一些基本性质.在此基础上给出了态滤子和态局部R0代数的概念,并利用态滤子刻画了态局部R0代数.推广了局部R0代数的相关理论.

R0代数;态R0代数;态滤子;态局部

1 引言

多值逻辑系统是20世纪30年代Lukasiewicz提出的.随着20世纪70年代模糊集概念的提出,模糊逻辑与模糊推理理论得到了发展.基于对模糊逻辑与经典逻辑本质区别的分析,1997年,王国俊[1]提出了模糊命题的一种形式演绎系统£∗,为了系统研究£∗,王国俊[2]引入了一种新的逻辑代数-R0代数.这为这类演绎系统的研究提供了代数模型.随后,很多学者[3-5]都对R0代数进行了研究.

作为多值逻辑中命题真值的平均度,1995年Mundici[6]提出了MV代数上态的概念.近年来,国内外很多学者致力于逻辑代数上态理论的研究.例如,2008年,刘练珍[14]研究了R0代数上的态存在问题.2007年,Flaminio和Montagna[7]用一种新的方法研究了MV代数上的态.他们在MV代数上定义了一个一元运算σ(称为内部态或者态算子),它是态的推广.随后,态算子在其他代数结构中进行了研究.例如,2011年Ciungu等[8]提出了态BL代数,它是态MV代数的推广.2015年,贺鹏飞、辛小龙[13]提出了态residuated lattices并研究了其相关性质.本文提出了态R0代数的定义,研究了它的性质,又定义了态滤子和态局部R0代数的概念,并利用态滤子刻画了态局部R0代数.

2 预备知识

定义2.1[2]设L=(L,∧,∨,′,→,0,1)是 (2,2,1,2,0,0) 型代数,若

(1)(L,∧,∨,0,1)是一个有界分配格;

(2)′是关于序≤而言的逆序对合对应;

(3)对于L中的任意元素x,y,z,有

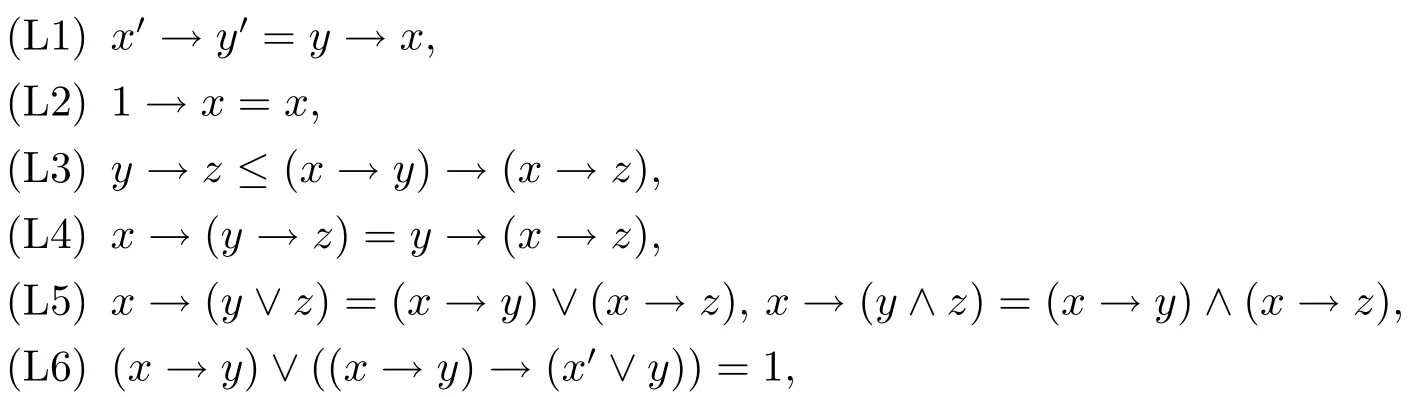
则称(L,∧,∨,′,→,0,1)为R0代数.以下简记为L.

在R0代数L中定义序关系”≤”为x≤y当且仅当x→y=1.

性质2.2[2]设L是R0代数,则以下结论成立：对任意的x,y,z∈L,

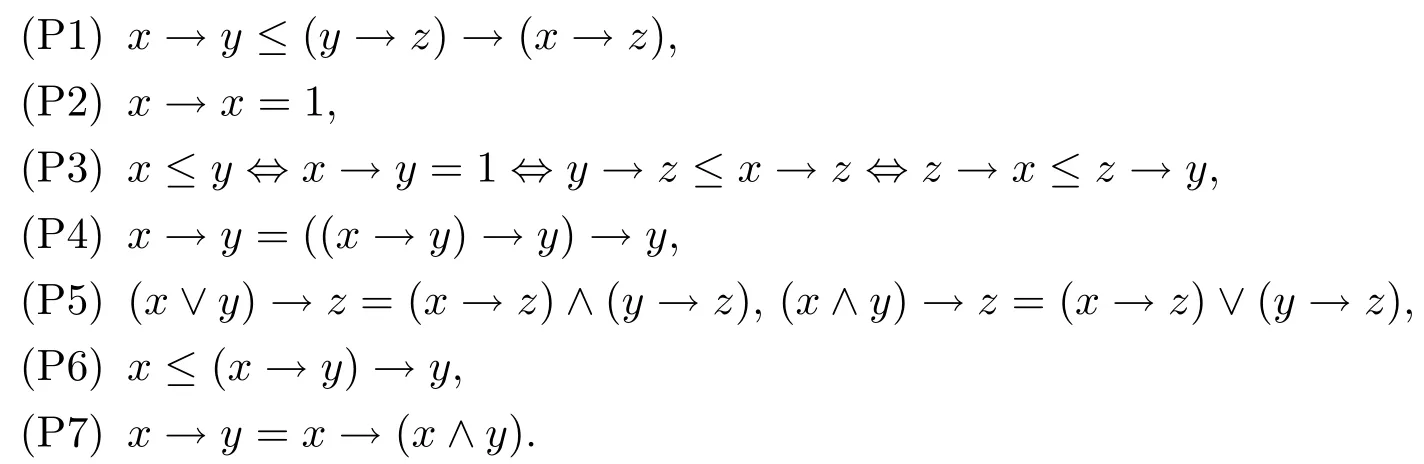
性质2.3[2]设L是R0代数,在L上定义x⊗y=(x→y′)′,则有对任意的x,y,z∈L,

定义2.4[9]设L是R0代数,F是L的非空子集,若以下条件成立：对任意的x,y∈F,

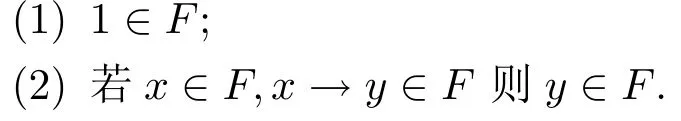
则称F为L的滤子.

设L是R0代数,F为L的滤子.若,则称F为真滤子.显然,F是真滤子当且仅当0当且仅当对任意的x∈L,x和x′不能同时属于F.若E是任意一个滤子,且F⊆E,有E=F或E=L,则称真滤子F为极大滤子.

引理2.5[10]设L是R0代数,F是L的非空子集,则F是L的滤子以下条件成立：对任意的x,y∈F,

(1)1∈F,

(2)若x∈F,x≤y,则y∈F,

(3)若x,y∈F,则x⊗y∈F.

推论2.6[10]设L是R0代数,F是L的滤子,定义二元关系RF为xRFy当且仅当x→y∈F和y→x∈F.则

(1)RF为L上的同余关系,

(2)L/F为一个R0代数,这里[x]表示x所在的RF等价类并且L/F={ [x]|x∈L}.

定义2.7[9]设L是R0代数,x∈L,使xm=0成立的最小自然数m叫做元素x的阶,记为ord(x).若这样的m不存在,则称x的阶为无限,即ord(x)=∞.

引理2.8[11]设L是R0代数,X是L的非空子集,称包含X的最小滤子为由X生成的滤子,记为〈X〉,则〈X〉={x∈L|x≥x1⊗x2⊗ ···⊗xn,存在x1,x2···xn∈X}.记L的所有滤子集为F(L),且F(L)(关于包含关系)可构成完备格.

引理2.9[9]设L为R0代数,F为L的任意一个真滤子,则F可延拓为一个极大滤子.

定义2.10[12]设L为R0代数,若L有唯一的极大滤子,则称L为局部的.

3 态R0代数

定义3.1设L是R0代数,σ：L→L为L上的自映射.若σ满足：对任意的x,y∈L,

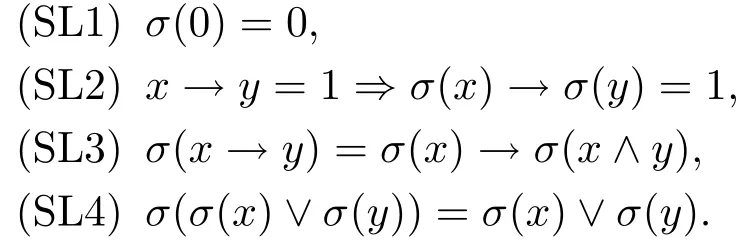
则称σ为L上的态算子,此时称(L;σ)为态R0代数.

设σ为L上的任意的态算子,Ker(σ)={x∈L|σ(x)=1}.若Ker(σ)={ 1},则称σ为忠实的.

例3.2设L为R0代数,由性质2.2可知,idL为L上的态算子.因此(L;idL)为态R0代数,即一个R0代数L可以看成是一个态R0代数.

例3.3设L={ 0,a,b,c,d,e,f,g,1},L上的偏序关系为0≤a≤c,d≤f≤1,0≤b≤d,e≤g≤1,其上的二元运算→和一元运算′的定义如下表所示

→ 0 a b c d e f g 1 0 1 1 1 1 1 1 1 1 1a g 1 g 1 1 g 1 1 1b f f 1 f 1 1 1 1 1c e g e 1 g e 1 g 1d d f g f 1 g 1 1 1e c c f c f 1 f 1 1f b d e f g e 1 g 1g a c d c f g f 1 1 1 0 a b c d e f g 1x 0 a b c d e f g 1x′ 1 g f e d c b a 0

容易验证(L,∧,∨,′,→,0,1)是R0代数.在L上定义σ如下

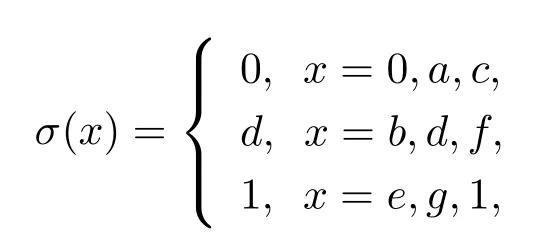
则容易验证σ是L上的态算子,即(L;σ)是态R0代数.

性质3.4设(L;σ)为态R0代数,则以下结论成立：对任意的x,y∈L,

(1)σ(1)=1,

(2)x≤y⇒σ(x)≤σ(y),

(3)σ(x′)=(σ(x))′,

(4)σσ(x)=σ(x),

(5)σ(σ(x)∧ σ(y))=σ(x)∧σ(y),

(6)σ(σ(x)→σ(y))=σ(x)→σ(y),

(7)σ(σ(x)⊗ σ(y))=σ(x)⊗ σ(y),

(8)σ(x→y)≤σ(x)→σ(y).特别地,若x,y可比较,则σ(x→y)=σ(x)→σ(y),

(9)若σ是忠实的,则x＜y⇒σ(x)＜σ(y),

(10)σ(L)=Fix(σ),这里 Fix(σ)={x∈L|σ(x)=x},

(11)σ(x⊗y)≥σ(x)⊗σ(y).特别地,若x,y可比较,则σ(x⊗y)=σ(x)⊗σ(y),

(12)Ker(σ)是L的滤子,

(13)σ(L)是L的子代数.

证 (1)由(SL2)可得σ(0→1)=σ(0)→σ(0∧1),即σ(1)=σ(0)→σ(0)=1.

(2)由x≤y可得x→y=1,又由(SL2)可知σ(x)→σ(y)=1即σ(x)≤σ(y).

(3) 由 (SL3)可知σ(x′)=σ(x→0)=σ(x)→σ(x∧0)=σ(x)→σ(0)=(σ(x))′.

(4) 由(SL1)和(SL4)可得σ(σ(x)∨ σ(0))=σ(x)∨σ(0),即σσ(x)=σ(x).

(5)由(SL4)和(3),

(6)由(SL3),(4)和(5)可得

(7)由(3)和(6)可得

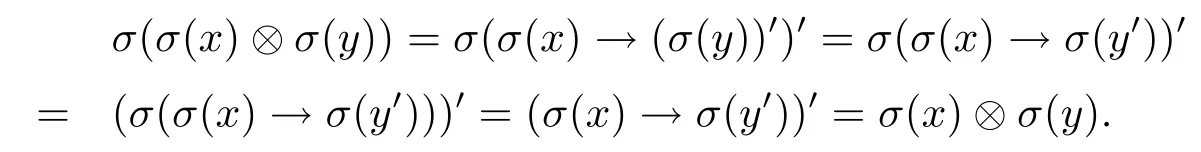
(8)由于x∧y≤y,即(x∧y)→y=1,由(SL2)可得σ(x∧y)→σ(y)=1即σ(x∧y)≤σ(y).由(P3)可知σ(x)→σ(x∧y)≤σ(x)→σ(y),又根据(SL3),σ(x→y)=σ(x)→σ(x∧y)≤σ(x)→σ(y).

若x≤y,则σ(x)≤σ(y)即σ(x)→σ(y)=1,σ(x→y)=σ(1)-1,所以σ(x→y)=σ(x)→σ(y).

若y≤x,则x∧y=y.由(SL3)可知,σ(x→y)=σ(x)→σ(x∧y)=σ(x)→σ(y).

(9)由x＜y可得σ(x)≤σ(y).假设σ(x)=σ(y),由 (SL3),σ(y→x)=σ(y)→σ(y∧x)=σ(y)→σ(x)=1即y→x∈Ker(σ)={ 1},则y→x=1,即y≤x,与条件矛盾.所以σ(x)＜σ(y).

(10)若对任意y∈ σ(L),则存在x∈L使得y=σ(x),σ(y)=σσ(x)=σ(x)=y,即y∈Fix(σ).若对任意y∈Fix(σ),即σ(y)=y,则y∈σ(L).所以σ(L)=Fix(σ).

(11) 由 (P3),(3)和 (8)可得σ(x⊗y)=σ(x→y′)′=(σ(x→y′))′≥ (σ(x)→σ(y′))′=σ(x)⊗σ(y).特别地,若x,y可比较,则由(3)和(8)得σ(x⊗y)=σ(x→y′)′=(σ(x→y′))′=(σ(x)→σ(y′))′=σ(x)⊗σ(y).

(12)由σ(1)=1可知1∈Ker(σ).任意x,y∈L,若x,x→y∈Ker(σ),则有σ(x)=1,σ(x→y)=1.σ(x)→σ(y)=1→σ(y)=σ(y),由 (7),σ(y)=σ(x)→σ(y)≥σ(x→y)=1,即σ(y)=1,所以y∈Ker(σ).则Ker(σ)为L的滤子.

(13)由(L1),(L4)和(1),(3),(5),(6)知σ(L)对运算∧,∨,′,→且对0,1封闭.所以σ(L)为L的子代数.

4 态R0代数上的态滤子

定义4.1设(L;σ)是态R0代数,F为L的滤子.若对任意的x∈F,有σ(x)∈F,则称F为(L;σ)的态滤子.设F为真态滤子,E是任意一个态滤子,若F⊆E,有E=F或E=L,则称F为(L;σ)的极大态滤子.记SF[L]为(L;σ)的所有态滤子的集合.

例4.2设F1={e,g,1},F2={c,f,1}为例3.2中L的子集,显然,F1,F2都是L的滤子.容易验证F1是(L;σ)的态滤子.而在F2中,c,f∈F2但σ(c)=0/∈F2,σ(f)=2,所以F2不是(L;σ)的态滤子.

设(L;σ)是态R0代数,X是L的非空子集,称包含X的最小态滤子为由X生成的态滤子,记为〈X〉σ.

定理4.3 设(L;σ)为态R0代数,X是L的非空子集.则〈X〉σ={x∈L|x≥(x1⊗σ(x1))n1⊗···⊗(xk⊗σ(xk))nk,xi∈X,ni≥ 1,k≥ 1}.

证证明和文献[8]中定理5.4的证明类似.

引理4.4设(L;σ)是态R0代数,F为(L;σ)的真态滤子,则F为极大态滤子当且仅当对任意的x/∈F,存在正整数n≥1使得(σ(x)n)′∈F.

证证明和文献[8]中定理5.4的证明类似.

定义4.5设(L;σ)为态R0代数,若(L;σ)有唯一的极大态滤子,则称(L;σ)为态局部的.

设(L;σ)是态R0代数,定义D(L;σ)={x∈L|∀n≥ 1,(σ(x))n＞0}.

注∀x∈L,x∈D(L;σ)当且仅当ord(σ(x))=∞.

引理4.6设(L;σ)为态R0代数,F是(L;σ)的真态滤子,则F⊆D(L;σ).

证任意x∈F,有σ(x)∈F,则对任意的n≥1,(σ(x))n∈F,又0/∈F,所以(σ(x))n/0即x∈D(L;σ).所以,F⊆D(L;σ).

引理4.7设(L;σ)为态R0代数,则下列结论等价.

(1)D(L;σ)是 (L;σ)的态滤子.

(2)对任意x,y∈L和n≥1,由(σ(x))n,(σ(y))n0能推出(σ(x⊗y))n/0.

证(1)⇒(2)任意x,y∈L,对任意的n≥1,若(σ(x))n,(σ(y))n0即x,y∈D(L;σ),则x⊗y∈D(L;σ).所以(σ(x⊗y))n0.

(2)⇒(1)显然1∈D(L;σ).设x,x→y∈D(L;σ),则对任意n≥ 1,有(σ(x))n,(σ(x→y))n＞0,由(2)可知[σ(x⊗(x→y))]n＞0.由于y≥x⊗(x→y),即σ(y)≥σ(x⊗(x→y)),所以(σ(y))n≥ [σ(x⊗(x→y))]n＞0.因此y∈D(L;σ)即D(L;σ)为滤子.设任意x∈D(L;σ)则对任意n≥1,有

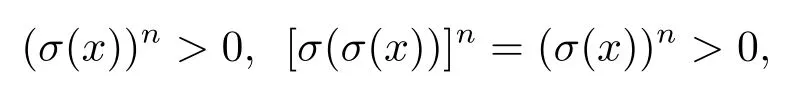
所以σ(x)∈D(L;σ).因此D(L;σ)为态滤子.

定理4.8设(L;σ)为态R0代数,则下列条件等价.

(1)D(L;σ)是态滤子;

(2)〈D(L;σ)〉σ是真态滤子;

(3)D(L;σ)是(L;σ)的唯一极大态滤子;

(4)(L;σ)是态局部的.

证(1)⇒(2)显然〈D(L;σ)〉σ=D(L;σ).由于0(L;σ),故〈D(L;σ)〉σ是真态滤子.

(2)⇒(3) 设〈D(L;σ)〉σ是真态滤子,由引理 4.6 知〈D(L;σ)〉σ⊆D(L;σ),又D(L;σ)⊆〈D(L;σ)〉σ,因此〈D(L;σ)〉σ=D(L;σ) 即D(L;σ) 为真态滤子. 假设F为 (L;σ) 的极大态滤子,即F⊆D(L;σ),由F的极大性知F=D(L;σ).因此D(L;σ)是(L;σ)的唯一极大态滤子.

(3)⇒(4)显然.

(4)⇒(1)设F为(L;σ)的唯一极大态滤子.设x∈D(L;σ),则〈x〉σ是真态滤子,〈x〉σ可以延拓为极大态滤子Fx,由唯一性知Fx=F,因此x∈F,所以D(L;σ)⊆F.又F⊆D(L;σ),故D(L;σ)=F.因此D(L;σ)为态滤子.

定理4.9设(L;σ)为态R0代数,(L;σ)是态局部的充要条件是对任意的x∈L,

证⇒设(L;σ)是态局部,由定理4.8知,D(L;σ)是态滤子.假设存在x∈L使得对任意n≥ 1,(σ(x))n＞0 且(σ(x′))n＞0,由引理4.7,(σ(x⊗x′))n＞0,而x⊗x′=0,(σ(x⊗x′))n=0矛盾.所以,任意的x∈L,

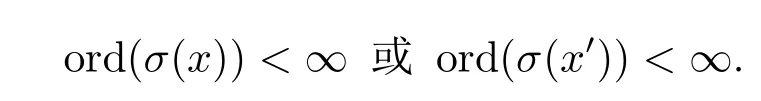
⇐显然 1∈D(L;σ). 设x,x→y∈D(L;σ),则有 (x⊗y′)′=x→y∈D(L;σ)即 ord(σ(x⊗y′)′)=∞, 由条件可得 ord(σ(x⊗y′))＜∞. 设 ord(σ(x⊗y′))=m1, 即(σ(x⊗y′))m1=0,又

因此 (σ(y′))m1≤[(σ(x))m1]′.x∈D(L;σ), 即对任意n≥ 1,(σ(x))n＞0, 从而对任意m＞1,[(σ(x))m1]m＞0,即 ord(σ(x))m1=∞,所以 ord[(σ(x))m1]′=m2＜∞,即[((σ(x))m1)′]m2=0,因此

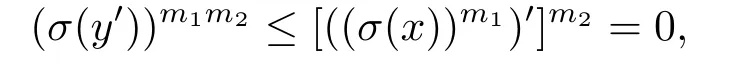
有 (σ(y′))m1m2=0,ord(σ(y′))＜∞,所以 ord(σ(y))=∞,即y∈D(L;σ). 设x∈D(L;σ),即 (σ(x))n＞0,(σ(σ(x)))n=(σ(x))n＞0,则σ(x)∈D(L;σ). 因此D(L;σ)为态滤子,由定理4.9知,(L;σ)是态局部的.

引理4.10设(L;σ)为态R0代数,F是(L;σ)的态滤子,σ′：L/F→L/F上的映射且σ′(x/F)=σ(x)/F,则 (L/F;σ′) 为态R0代数.

证由推论2.6可知L/F为R0代数.又σ′(0/F)=σ(0)/F=0/F,当x→y=1时,

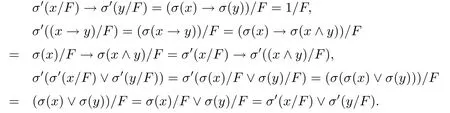
因此由定义3.1可知σ′为L/F上的态算子,所以(L/F;σ′)为态R0代数.

定理4.11设(L;σ)为态R0代数,F是(L;σ)的态滤子,则以下条件是等价的.

(1)(L/F;σ′)是态局部R0代数,

(2)若对任意x,y∈L,x⊗y′∈F,则存在正整数n≥1使得((σ(x))n)′∈F或((σ(y))n)′∈F.

证(1)⇒(2)设(L/F;σ′)为态局部R0代数且x⊗y′∈F,即y→x′∈F,因此

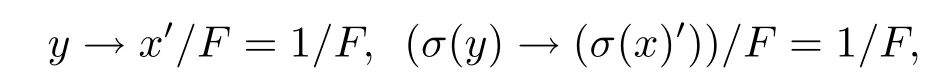
即σ(y)/F≤(σ(x))/F.假设对任意n≥1有((σ(x))n)′/∈F,(σ(x))n)′/F/=1/F,即(σ(x))n/F/=0/F,由定理4.9,ord(σ′(x′/F))＜∞,即存在m≥ 1 使得

即 (σ(y))m/F=0/F,所以 ((σ(y))m)′/F=1/F,即 ((σ(y))m)′∈F.

(2)⇒(1) 由于(x⊗x′)′=1∈F,故存在n≥ 1 使得 ((σ(x))n)′∈F或 ((σ(x′))n)′∈F,即σ(x)n/F=(σ′(x/F))n=0/F或 (σ′(x′/F))n=0/F. 由定理 4.9 知 (L/F;σ′) 为态局部R0代数.

定理4.12设(L;σ)为态R0代数,F为(L;σ)的一个态滤子,则以下条件等价.

(1)(L;σ)为态局部的,

(2)对任意x,y∈L,若x⊗y′∈F,则存在正整数n≥1使得((σ(x))n)′∈F或((σ(y))n)′∈F.

证(1)⇒(2) 设(L;σ)为态局部的且F为(L;σ)的真态滤子.由引理4.6知,F⊆D(L;σ).由定理4.8知,D(L;σ)为态滤子.若x⊗y′∈F⊆D(L;σ),则对任意n≥ 1,(σ(x⊗y)′)n＞0即ord(σ(x⊗y))＜∞,因此存在n≥ 1使得(σ(x⊗y))n=0,即(σ(x))n=0 或 (σ(y))n=0,从而 ((σ(x))n)′=1∈F或 ((σ(y))n)′=1∈F.

(2)⇒(1)注意到{ 1}是(L;σ)的态滤子,σ′为上述所定义的映射,由定理4.10知(L/{1};σ′) 为态局部R0代数. 又 (L;σ)(L/{1};σ′),所以 (L;σ)为态局部R0代数.

由定理4.11和定理4.12,有以下推论.

推论4.13设(L;σ)为态R0代数,F是(L;σ)的态滤子,σ′：L/F→L/F上的映射且σ′(x/F)=σ(x)/F,则以下条件是等价的.

(1)(L;σ)为态局部的,

(2)(L/F;σ′)是态局部R0代数,

(3)对任意x,y∈L,若x⊗y′∈F,则存在正整数n≥1使得((σ(x))n)′∈F或((σ(y))n)′∈F.

[1]王国俊.模糊命题演算的一种形式演绎系统[J].科学通报,1997,42(10)：1041-1045.

[2]Wang G J.Non-classcal mathematical logic and approximate reasoning[M].Beijing：Science Press,2000.

[3]马学玲,詹建明.模糊参数模糊软R0代数[J].模糊系统与数学,2013,25-29.

[4]Ma X L,Zhan J M,Xu Y.Generalized fuzzy filters ofR0algebras[J].Soft Comput.,2007,1079-1087.

[5]李志伟,李桂华.模糊蕴涵代数的结构特征[J].数学杂志,2008,28(6)：701-705.

[6]Mundici D.Averaging the truth-value in Lukasiewicz logic[J].Studia Logica,1995,55(1)：113-127.

[7]Flaminio T,Montagna F.An algebraic approach to state on MV-algebras[J].Fuzzy Logic,2007：201-206.

[8]Ciungu L C,Dvurecenskij A.State BL-algebras[J].Soft Comput.,2011,15：619-634.

[9]裴道武,王国俊.形式系统£∗的完备性及其应用[J].中国科学(E辑),2002,32(1)：56-64.

[10]裴道武.R0代数的MP滤子与同余关系[J].模糊系统与数学,2002,16(专辑)：2002,16：22-25.

[11]张家录.R0代数上的MP滤子格[J].模糊系统与数学,2006：26-33.

[12]刘练珍,李开泰.局部R0代数[J].数学研究与评论,2005：538-542.

[13]He P F,Xin X L.On state residuated lattices[J].Soft Comput.,2015,19(8)：1-12.

[14]Liu L Z,Zhang X Y.State onR0-algebras[J].Soft Comput.,2008,12：1099-1104.

ON STATER0-ALGEBRAS

QIN Yu-jing1,XIN Xiao-long1,HE Peng-fei2
(1.School of Mathematics,Northwest University,Xi’an 710127,China)(2.School of Mathematics and Information Science,Shaanxi Normal University,Xi’an 710119,China)

In this paper,we study the problems of state operators.By using the method of introducing internal states on MV-algebras,we introduce the state operators onR0-algebras and define the stateR0-algebras,which are generalization ofR0-algebras.We give some non-trivial examples of stateR0-algebras and study some basic properties of them.Based on the above arguments we define the state filters and state localR0-algebras.We characterise the state localR0-algebras by the state filters,which generalizes the theory of localR0-algebras.

R0-algebra;stateR0-algebra;state fi lter;state local

on：06F25

O141.1

A

0255-7797(2017)04-0881-08

2015-07-09接收日期：2016-01-06

国家自然科学基金资助(11571281).

秦玉静(1991-),女,河南焦作,硕士,主要研究方向：逻辑代数.