SOME OPERATOR INEQUALITIES OF MONOTONE FUNCTIONS CONTAINING FURUTA INEQUALITY
YANG Chang-sen,YANG Chao-jun
(College of Mathematics and Information Science,Henan Normal University,Xinxiang 453007,China)
SOME OPERATOR INEQUALITIES OF MONOTONE FUNCTIONS CONTAINING FURUTA INEQUALITY
YANG Chang-sen,YANG Chao-jun
(College of Mathematics and Information Science,Henan Normal University,Xinxiang 453007,China)
In this paper,we study the relations between the operator inequalities and the operator monotone functions.By using the fundamental conclusions based on majorization,namely,product lemma and product theorem for operator monotone functions,we can give some operator inequalities.This result contains the Furuta inequality,which has a huge impact on positive operator theory.
operator monotone function;product lemma;product theorem;majorization
1 Introduction
LetJbe an interval such thatJ/(-∞,∞).P(J)denotes the set of all operator monotone functions onJ.We setP+(J)={f∈P(J)|f(t)≥0,t∈J}.Iff∈P+(a,b)and-∞<a,thenfhas the natural extension to[a,b),which belongs toP+[a,b).We therefore identifyP+(a,b)withP+[a,b).
It is well-known that iff(t)∈P+(0,∞),thenare both inP+(0,∞),and that iff(t),φ(t),φ(t)are all inP+(0,∞),then so are

andf(t)αφ(t)1-αfor 0<α<1(see[1-5]).Throughout this work,we assume that a function is continuous and increasing means “strictly increasing”.Further more,for convenience,letB(H)denote theC∗-algebra of all bounded linear operators acting on a Hilbert spaceH.A capital letterAmeans an element belongs toB(H),Φ means a positive linear map fromB(H)toB(H)and we assume Φ(I)=Ialways stand(see[7,8]).In this paper,we also assume thatJ=[a,b)orJ=(a,b)with-∞≤a<b≤+∞.
De fi nition 1.1[9,10]Letdenote the following sets,respectively,
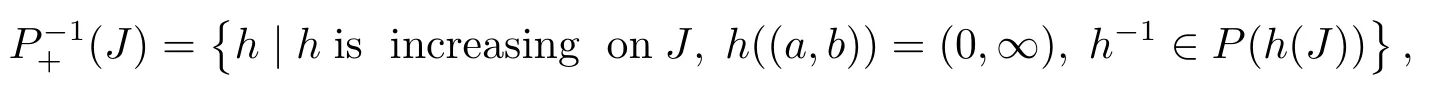
whereh-1stands for the inverse function ofh.
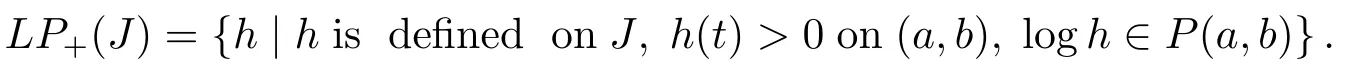
De fi nition 1.2Leth(t)andg(t)be functions defined onJ,andg(t)is increasing,thenhis said to be majorized byg,in symbolh≤gif the compositeh◦g-1is operator monotone ong(J),which is equivalent to

Lemma 1.1(Product lemma)(see[9,10])Leth,gbe non-negative functions defined onJ.Suppose the producthgis increasing,(hg)(a+0)=0 and(hg)(b-0)=∞.Then

Moreover,for everyψ1,ψ2inP+[0,∞),

Theorem 1.1(Product theorem)(see[9,10])

Further,letgi(t)∈LP+(J)for 1≤i≤mandhj(t)∈P-1+(J)for 1≤j≤n.Then for everyψi,φj∈P+[0,∞),we have
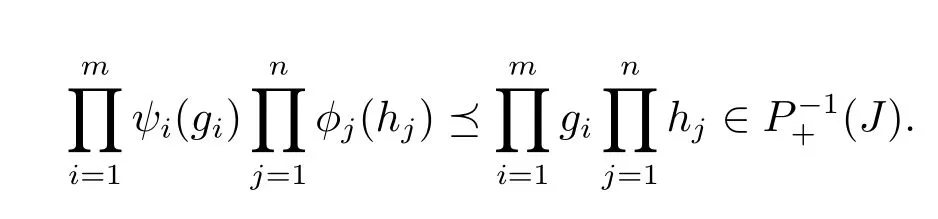
2 Main Results
Before to prove our main results,we give the following lemmas.
Lemma 2.1(L-H inequality)(see[2,12])If 0≤α≤1,A≥B≥0,thenAα≥Bα.
Lemma 2.2(Furuta inequality)(see[6,9])LetA≥B≥0,then

wherer≥0,p≥1 with
Lemma 2.3(Hansen inequality)(see[13])LetXandAbe bounded linear operators onH,and such thatX≥ 0,‖A‖≤1.Iffis an operator monotone function on[0,∞),then
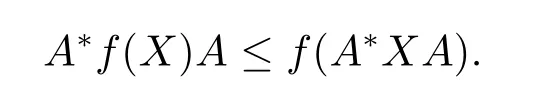
Theorem 2.1PutJ/=(-∞,∞),,fi∈P+(J),i=1,2,···,n,,andkn(t)=f1(t)f2(t)···fn(t).Ifh(t)is defined onJsuch that,then
(i)the functionφnon(0,∞)defined by

belongs toP+(0,∞);
(ii)ifA≤C≤B,then
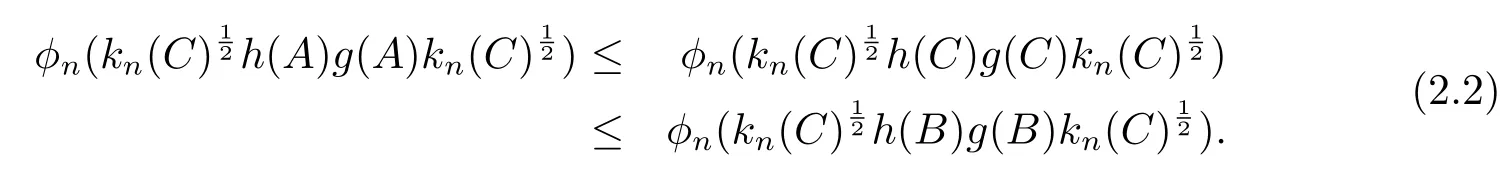
Proof(i)Sincef1(t)f1(t)h(t),by product lemmah(t)f1(t)h(t),thereforeh(t)is nondecreasing.When,since,we haveη(t)g(t).Now puttingψ0(s)=s,ψ1(g)=η,ψ2(f1h)=f1,obviously,we haveψ0,ψ1,ψ2∈P+(0,∞).By takingsinψ0(s)asf2···fn,and from product theorem,we obtain

Therefore we haveφnbelongs toP+(0,∞)forφngiven in(i).
Wheng(t)=f1(t),by takingψ0(s)=s,ψ1(g(t)h(t))=η(t),we haveψ0,ψ1∈P+(0,∞),and thenφn∈P+(0,∞)by product theorem.
(ii)First we prove that

Sinceφn,kn,h,gare all nonnegative,nondecreasing functions andJis a right open interval,by consideringC+ϵ,B+ϵ,we may assume that,h(C),h(B),g(C),g(B)are positive semi-de fi nite and invertible.Through(i),


This implies the right part of(2.2)holds forn=1.Next we assume the right part of(2.2)holds forn-1.Sinceandand this means that there existssuch thatfn(t)= Ψn(kn-1(t)η(t)).Puts=kn-1(t)η(t),we can obtain.Since the following inequality holds

Denote the left side of the upper inequalities asH,the right one asK,we have

ByH=φn-1(kn-1(C)h(C)g(C))=kn-1(C)η(C),we obtain
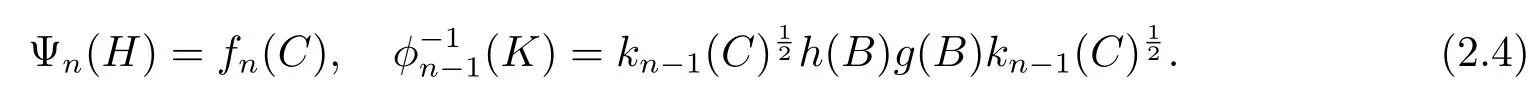
By Lemma 2.3 again,we obtain

From the above inequalities and(2.4),we get
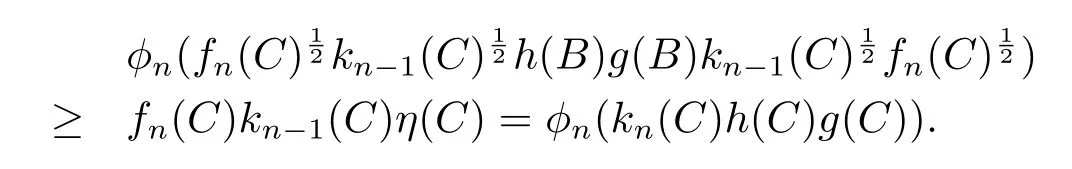
Therefore the right part of(2.2)holds forn,one can proof the left part of(2.2)similarly.
RemarkIn Theorem 2.1,letn=2,f1(t)=g(t)=1,f2(t)=tr(r≥0),h(t)=tp(p≥1),andη(t)=t,then we haveφ2(tp+r)=t1+r.So Furuta inequality can be obtained by(2.2)and L-H inequality.
Lemma 2.4(see[10,11])PutJ(-∞,∞),theng∈LP+(J)if and only if there exists a sequence{gn}of a fi nite product of functions inP+(J)which converges pointwise togonJ,further more,{gn}converges uniformly togon every bounded closed subinterval ofJ.
Theorem 2.2PutJ(-∞,∞),f(t)>0 fort∈Jandη(t),h(t),k(t),g(t)are nonnegative functions onJsuch that,then
(i)the functionφon(0,∞)defined by
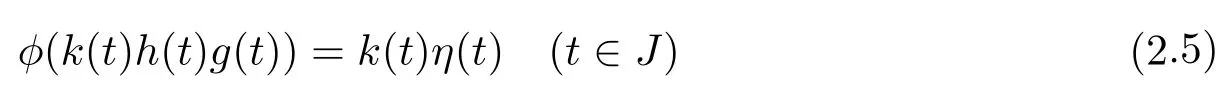
belongs toP+(0,∞);
(ii)IfA≤C≤B,then forφ∈P(0,∞)such thatφ≤φon(0,∞),
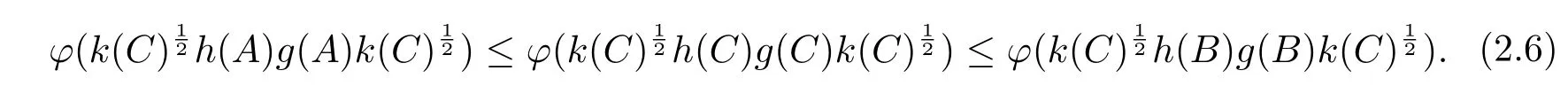
Proof(i)First consider,thenk=lfand
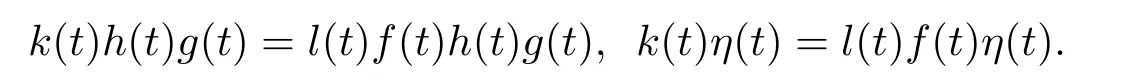
Letψ0(s)=s,ψ1(f(t)h(t))=f(t),ψ2(g(t))=η(t),thenψ0,ψ1,ψ2∈P+(0,∞).By takings=l(t)and applying product theorem,we get

which equals tok(t)η(t)≤k(t)h(t)g(t).So we haveφ∈P+(0,∞)forφsuch that
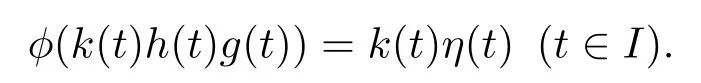
Ifg=f,takingψ0(s)=s,ψ1(h(t)g(t))=η(t),obviously,we haveψ0,ψ1∈P+(0,∞),and thenψ0(k)ψ1(hg).Hence we also haveφ∈P+(0,∞)from product theorem.
(ii)From Lemma 2.4,we obtain there exists a sequence{ln},whereln(t)is a fi nite product of functions inP+(J),such thatln(t)converges ponitwise tol(t).Putkn(t)=f(t)ln(t)then we easily getkn(t)converges tok(t)=f(t)l(t).De fi neφn(kn(t)h(t)g(t))=kn(t)η(t)(t∈J),φn∈P+(0,∞).By Theorem 2.1,we have
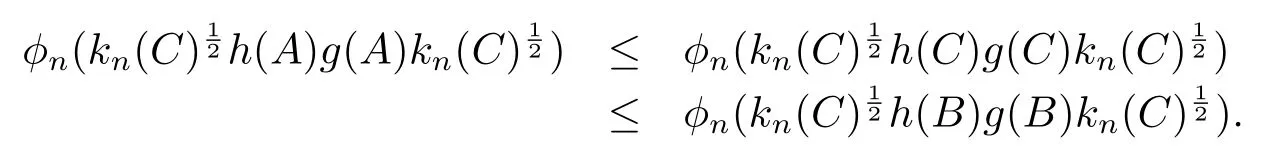
Lemma 2.5(Choi inequality)(see[6,7])Let Φ be a positive unital linear map,then
(C1)whenA>0 and-1≤p≤0,then Φ(A)p≤Φ(Ap);
(C2)whenA≥ 0 and 0≤p≤1,then Φ(A)p≥ Φ(Ap);
(C3)whenA≥ 0 and 1≤p≤2,then Φ(A)p≤Φ(Ap).
Corollary 2.1PutJ/=(-∞,∞),f(t)>0 fort∈Jandη(t),h(t),k(t),g(t)are nonnegative functions onJsuch that,the functionφon(0,∞)defined as(2.5),Φ is a positive unital
linear map.If

then forφ∈P(0,∞)such thatφ≤φ,

ProofBy Choi inequality and L-H inequality,we obtain

Corollary 2.2Put
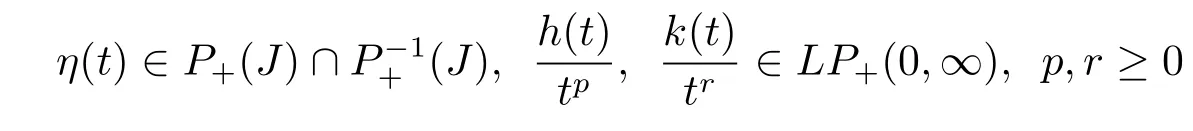
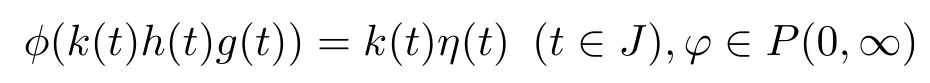
such that.Then(2.5)and(2.6)in Theorem 2.2 hold.
ProofPutc=min{ 1,p},thenf(t)=t1-c∈P+(0,∞).Thus we get

which means the conditions of Theorem 2.2 is satis fi ed.Therefore(2.5)and(2.6)in Theorem 2.2 hold.
Corollary 2.3Put,p,r≥0 andp+r≥1,s≥1,we obtain
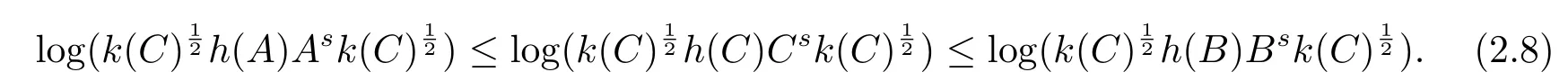
ProofPutg(t)=ts(s≥1),η(t)=tin Corollary 2.2.Then we only need to show logs≤φ(s),s∈(0,∞).The de fi nition ofφis given in(2.5).The upper majorization relationship is equivalent to

It is obviously that logk(t),logh(t),logtsare operator monotone on(0,∞)and,then

Therefore(2.8)holds.
[1]Bhatia R.Matrix analysis[M].New York:Springer,1996.
[3]Horn R A,Johnson C R.Matrix analysis[M].Cambridge:Cambridge Univ.Press,1985.
[4]Rosenblum M,Rovenyak J.Hardy classes and operator theory[M].Oxford:Oxford Univ.Press,1985.
[5]Pedersen G K.Some operator monotone functions[J].Proc.Amer.Math.Soc.,1972,36:309-310.
[6]Choi M D.Some assorted inequalities for positive linear map onC∗-algebras[J].J.Oper.The.,1980,4:271-285.
[7]Choi M D.A Schwarz inequality for positive linear maps onC∗-algebras[J].Illinois.J.Math.,1974,18:565-574.
[8]Ando T.Concavity of certain maps on postive de fi nite matrices and applications to hadamard products[J].Linear Alg.Appl.,1976,26:203-241.
[9]Uchiyama M.A new majorization between functions,polynomials,and operator inequalities[J].J.Funct.Anal.,2006,231:221-244.
[10]Uchiyama M.A new majorization between functions,polynomials,and operator inequalities II[J].J.Math.Soc.Japan,2008,60:291-310.
[11]Uchiyama M.Operator inequalities:from a general theorem to concrete inequalities[J].Linear Alg.Appl.,2015,465:161-175.
[12]Yang C.Inequalities relating to means of positive operators[J].J.Math.,1996,16(4):467-474.
[13]Hensen F.An operator inequality[J].Math.Ann.,1980,246:249-250.
一些蕴含Furuta不等式的算子单调函数的算子不等式
杨长森,杨朝军
(河南师范大学数学与信息科学学院,河南新乡 453007)
本文研究了算子不等式与算子单调函数之间的联系.利用关于算子单调函数的乘积引理,乘积定理等基本控制原理,给出许多算子不等式,这些不等式可包含正算子理论中应有十分广泛的Furuta不等式.
算子单调函数;积引理;积定理;控制
O177.1
on:47A62;47A63
A Article ID: 0255-7797(2017)04-0698-07
date:2015-09-21Accepted date:2015-12-11
Supported by National Natural Science Foundation of China(11271112;11201127)and Technology and the Innovation Team in Henan Province(14IRTSTHN023).
Biography:Yang Changsen(1965-),male,born at Xinxiang,Henan,professor,major in functional analysis.
- 数学杂志的其它文章
- THE GROWTH ON ENTIRE SOLUTIONS OF FERMAT TYPE Q-DIFFERENCE DIFFERENTIAL EQUATIONS
- A MODIFIED BIC TUNING PARAMETER SELECTOR FOR SICA-PENALIZED COX REGRESSION MODELS WITH DIVERGING DIMENSIONALITY
- FINITE GROUPS WHOSE ALL MAXIMAL SUBGROUPS ARE SMSN-GROUPS
- GLOBAL BOUNDEDNESS OF SOLUTIONS IN A BEDDINGTON-DEANGELIS PREDATOR-PREY DIFFUSION MODEL WITH PREY-TAXIS
- ON PROJECTIVE RICCI FLAT KROPINA METRICS
- 态R0代数

