基于观点传播的改进相似性计算评分预测方法

艾 均, 李林志, 苏 湛, 邬春学

(上海理工大学 光电信息与计算机工程学院,上海 200093)

基于观点传播的改进相似性计算评分预测方法

艾 均, 李林志, 苏 湛, 邬春学

(上海理工大学 光电信息与计算机工程学院,上海 200093)

通过研究网络结构上的观点传播与协同过滤算法,基于对观点传播算法的优化,提出了基于用户相似和物品相似推荐系统评分预测算法.设计的算法修正了现有相似研究中在目标比较相似时,相似性结果为零的问题,将用户(或物品)的相似度定义为用户(或物品)间的观点数目和差异在相应复杂网络中的传播结果,并提出了相应的推荐算法.在MovieLens数据集上的实验结果证明,提出的算法与几种典型的现有方法相比较,具有更高的准确性,并且优于观点传播算法.

复杂网络; 推荐系统; 评分预测; 观点传播; 相似度

随着互联网信息技术的高速发展,人们已经进入到信息过载[1-2]的时代.面对海量的信息,对信息消费者而言,能找到自己喜欢的信息是一个巨大挑战,同时对信息生产者来说,产生用户感兴趣的信息并推送给用户也是一个挑战.在此情况下,推荐系统显得尤为重要,它联系用户和物品,发现用户兴趣点并推荐其感兴趣的信息,解决信息过载问题.

推荐系统中研究和应用最广泛的是协同过滤算法[3-4],此外,基于隐语义模型[5]的算法自Netflix比赛以来也得到研究者的青睐.最近,基于网络结构[6]的推荐算法由于其更高的计算效率和准确率,逐渐引起学者的广泛关注.它是将用户和物品看成抽象的网络节点,通过构造一个用户-物品网络,利用物理学的方法研究个性化推荐.如Zhang等[7-8]加入用户对物品的打分信息,实现了基于热传导和物质扩散的推荐算法;Zhou等[9]通过结合物质扩散和热传导,提高了推荐算法的准确性和多样性;Huang等[10]在协同过滤算法中加入扩散动力学方法,部分解决了数据稀疏性问题.最近很多研究者用网络的方法[11-13]研究个性化推荐算法也取得了不错的成就.文献[11]将对象-用户网络模型中节点之间的关系作为研究的重点,研究了对象与对象的关系,用户与用户的关系,以及对象与用户之间的关系,从异质网络节点关系出发设计了新的方法.文献[12]应用网络模型,混合了质量扩散(mass diffusion,MD)和热传导(heat conduction,HC)方法,研究了不同权重对混合算法效果的影响.文献[13]设计了一个参数来调节扩散的倾向性.上面的算法主要研究了推荐列表,在评分预测方面的研究较少.

本文基于网络结构的观点传播理论[8]和观点传播过程的用户相似算法[12],发现在进行相似性计算时,现有的一些算法会在2个对象比较相似的情况下,出现相似性为零的计算结果.为了解决这一问题,本文改进了算法相似性的计算方法,避免了这一问题的出现,提出了基于观点传播的物品相似算法,并与协同过滤结合,预测用户对物品的评分.实验结果证明,与改进前的算法和传统的协同过滤算法比较,本文所用算法的准确率均有提高,并且算法的时间复杂度较低.

1 研究方法

本文研究观点的传播过程与协同过滤结合的推荐算法,基于传播的用户相似评分预测方法[12],在此基础上修改了缺陷,降低了算法的误差率,并提出了基于传播的物品相似推荐算法.

首先讨论基于用户观点传播(user opinion spreading,UOS)的推荐算法.假设一个推荐系统中有m个用户和n个物品,记用户和物品的集合分别为U={u1,u2,…,um}和O={o1,o2,…,on},则用户对物品的评分矩阵记为R={riα}∈Rm,n,其中,riα表示用户i对物品α的评分值,值为整数,范围属于[1,5].另外,设置一个与评分矩阵对应的矩阵A={aiα}∈Rm,n,若用户i对物品α评过分,则aiα为1;否则,为0.将用户集合和物品集合放到一个网络中,则ki和kα分别表示用户和物品的度值.

在利用用户对物品的评分信息时,需要考虑每个用户对物品的观点是不同的.例如,有些用户比较苛刻,属于完美主义者,对物品的评分普遍偏低;而有些用户没有那么苛刻,经常会给出较高的分值.所以,客观地评分实际受个人主观的影响.为了消除这种不利影响,可通过公式将评分归一化

(1)

式中:ri,max和ri,min代表用户i评分记录中的最高分和最低分;eiα为用户评分归一化之后的结果,若最高分与最低分相等,可将归一化值赋为0,eiα∈[-1,1].

通过归一化公式,用户的评分值范围变为-1～1之间,此时的值代表了用户的客观评价.例如,用户i评过的最高分和最低分为5和3,而用户j评过的最高分和最低分为3和1,他们对于同一物品α的真实评分都是3,此时,对用户i而言,3分是其评分记录的最低分,说明他不喜欢该物品;用户j的3分却是其评分记录的最高分,代表他比较喜欢该物品.通过归一化后,eiα=-1和ejα=1,可以表示他们之间的差异.

文献[12]使用资源分配和评分结合方法计算用户间的相似性.

(2)

式中:sij表示用户i对用户j的影响,可看作是用户i与用户j的相似度.

归一化后,用户评分乘积越大,共同评过分的物品越多,表示用户越相似.但用户间的影响是有向的,即sij≠sji.为了消除相似度为负值对预测值的影响,定义相似矩阵为Smm={sij},sij为负数时,则赋值为0,且将用户自身的相似度也变为0.

用户对物品的的评分预测为

(3)

这与协同过滤算法很相似,都是利用与用户最相似的邻居的评分预测用户对物品的评分值.

1.1 基于观点传播的用户相似算法

(4)表1 MovieLens训练集上归一化值为0占总评分数目的比例Tab.1 Proportion of normalized-value zero in the total user-item ratings of MovieLens training set

用1-|eiα-ejα|代替eiαejα,取值范围不变,但更精确地表达了用户间的相似程度.例如,用户i、用户j和用户k的最高、最低评分均为5和1,但对物品α的评分分别为3,3,5,故归一化后的值分别为eiα=0,ejα=0,ekα=1.计算改进前,用户j和用户k对用户i的影响则均为0,无法区分评分值不同用户间的相似程度;而改进后用户j对用户i的影响为1,用户k对用户i的影响为0,这与直观用户评分值表达的含义一样,提高了用户相似度的准确率.基于观点传播的用户相似(US-OS)算法是用户观点传播(UOS)算法的改进,并且取得了更好的效果.

1.2 基于观点传播的物品相似算法

基于邻域的协同过滤算法有2种:基于用户相似的协同过滤和基于物品相似的协同过滤.并且通过分析基于皮尔逊相关系数的协同过滤算法,发现基于物品相似的协同过滤的评分预测效果更好;另外,在真实的电影网站或图书网站中,用户的数目要远远多于物品数目,利用物品相似进行推荐,在时间复杂度上要小很多.因此,本文通过基于传播过程的用户相似算法,提出基于传播过程的物品相似算法.

基于物品相似的推荐算法,本质上是利用用户对物品的历史评分记录,建立一个物品的相似矩阵,在给用户推荐某个物品时,利用用户的历史评分记录,找到与该物品最相似的n个物品,通过用户对该物品邻居的评分,预测用户对该物品的评分值.在计算2个物品相似度时,必须是一个用户同时对这2个物品评过分,因此,在评分的归一化公式上,仍然可以使用式(1).

基于观点传播的物品相似IS-OS算法的相似度公式为

(5)

式中:sαβ表示物品α对物品β的影响,可看作是物品α与物品β的相似度.

但物品相似度是有向的,即2个物品间的影响是不同的.为了消除相似度为负值对预测值的影响,定义相似矩阵为Snn={sαβ},将sαβ为负数的值全部赋值为0.用户对物品的评分预测式与式(3)类似.

(6)

为了比较本文所用算法的优劣,分别与基于Pearson[14]相关系数的用户相似算法和物品相似算法比较,实验结果证明,本文所用算法降低了评分预测误差.基于Pearson相关系数的用户相似度和基于Pearson相关系数的物品相似度分别为

(7)

(8)

Pearson相关系数的取值范围为[-1,1].

2 实验结果与讨论

使用MovieLens 100k数据集验证所用算法的准确性,该数据集包括943个用户对1 682部电影进行的100 000条评分记录,评分值是1～5的整数,并且保证每个用户至少对20部电影评过分,数据集的数据稀疏度为93.70%.为了验证算法,使用折5交叉验证方法[15],将用户-物品评分记录随机地平均分成5组,使用其中的4组作为训练集,1组作为测试集,依次将每组作为测试集,并取5次结果的平均值作为最终的结果.

(9)

(10)

虽然MAE计算和理解简单,但存在一定的局限性,MAE低的推荐系统,只能说明该系统更擅长预测低分商品的评分[16].RMSE指标加重了对预测不准评分的惩罚,对系统的要求更苛刻.

将相似度为负数赋值成0的优化[17],更能提高算法的准确度.本文中所有的推荐算法均采用该方法,因此,将改进的皮尔逊用户协同过滤(UCF)算法简记为UCF-Pearson-Opt,将改进的皮尔逊物品协同过滤(ICF)算法简记为ICF-Pearson-Opt.将用户观点传播记为UOS,而基于UOS改进的观点传播的用户相似算法记为US-OS,并将本文新提出的基于观点传播的物品相似算法记为IS-OS.

为了比较不同算法的预测效果,本文计算了5种算法在不同邻居数目的平均绝对误差和均方根误差,结果如图1和图2所示.

在基于用户相似的推荐算法中,本文所用的基于UOS算法改进的US-OS算法的效果最好,在用户相似邻居个数n=40时得到最低的误差,MAE=0.734 3,RMSE=0.936 1,并且随着用户相似邻居个数的增加,曲线接近水平增长,说明US-OS算法的稳定性较好.US-OS算法的误差比UOS算法的更低,MAE和RMSE分别提高了0.88%和0.8%,说明本文所用改进方法的有效性.而传统的基于优化的皮尔逊用户协同过滤算法的效果最差,US-OS算法的MAE比其提高了1%,RMSE比其提高了1.5%,并且算法的时间复杂度并不高.

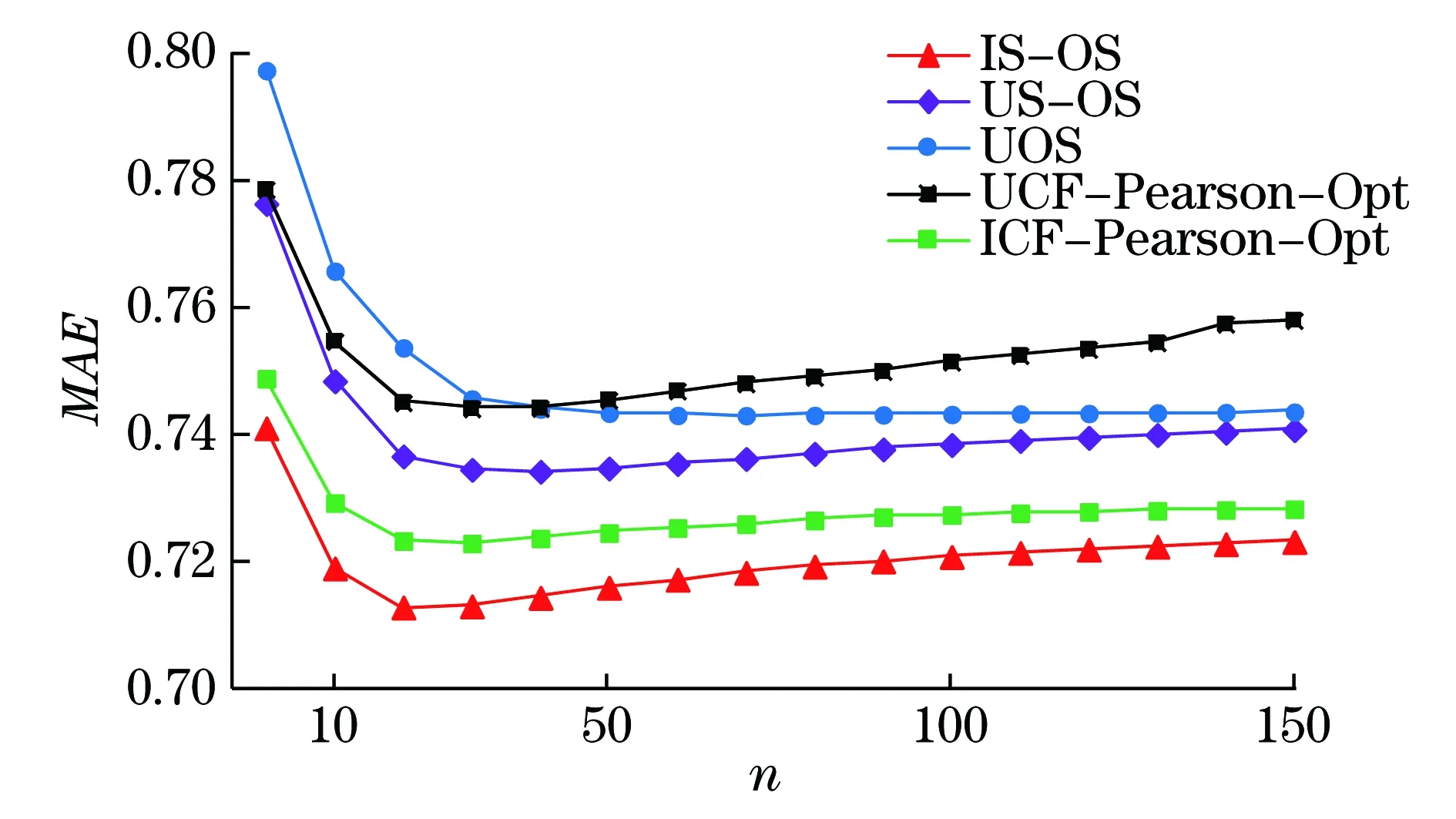
图1 5种算法在不同邻居个数下的平均绝对误差Fig.1 Mean average error results of five algorithms with different number of neighbors

图2 5种算法在不同邻居个数下的均方根误差Fig.2 Root mean square error of five algorithms with different number of neighbors

在基于物品相似的推荐算法中,本文所提出的基于观点传播的物品相似(IS-OS)推荐算法的效果最好.在物品相似邻居个数n=20时得到最低的MAE=0.713,而当n=30时得到最低的RMSE=0.910 9,并且随着物品相似邻居个数的增加,曲线接近水平增长,说明IS-OS算法的稳定性较好.比较传统的基于优化的皮尔逊物品协同过滤算法,IS-OS算法的MAE比其提高了1%,RMSE比其提高了1.15%.

3 结 论

综合5种算法的结果可知,IS-OS算法的效果最好,比US-OS算法的MAE提高了2.1%,RMSE提高了2.5%.综上可得结论:在MoiveLens 100k数据集上,基于物品相似的推荐算法要优于基于用户相似的推荐算法;基于物理学理论中的传播过程相似度计算方法要优于传统的皮尔逊相关系数相似度计算方法;采用评分数值归一化方法和相似度有向方法能有效提高算法的准确度.

研究了基于用户观点传播的推荐算法,针对其中的部分缺陷,提出改进的方法,命名为基于传播过程的用户相似(US-OS)推荐算法,并提出基于传播过程的物品相似(IS-OS)推荐算法.在MoiveLens数据集上的实验证明,US-OS算法在n=40时,得到最好的效果,MAE和RMSE分别为0.734 3和0.936 1,相比传统的皮尔逊用户协同过滤算法的MAE和RMSE分别提高了1%和1.5%.IS-OS算法在以上5种算法中效果最好,在n=20时,最低的MAE=0.713,n=30时,最低的RMSE=0.910 9,相比传统的皮尔逊物品协同过滤算法的MAE和RMSE分别提高了1%和1.15%.且比US-OS算法的MAE和RMSE分别提高了2.1%和2.5%.由此证明了本文所提算法的有效性,并且证明了在MoiveLens数据集上,基于物品相似的推荐算法要优于基于用户相似的推荐算法.

[1] JONES Q,RAVID G,RAFAELI S.Information overload and the message dynamics of online interaction spaces:a theoretical model and empirical exploration[J].Information Systems Research,2004,15(2):194-210.

[2] FENG L,HU Y Q,LI B W,et al.Competing for attention in social media under information overload conditions[J].PLoS One,2015,10(7):e0126090.

[3] LINDEN G,SMITH B,YORK J.Amazon.com recommendation:item-to-item collaborative filtering[J].IEEE Internet Computing,2003,7(1):76-80.

[4] HUANG Z,ZENG D,CHEN H.A comparison of collaborative-filtering recommendation algorithms for E-commerce[J].IEEE Intelligent Systems,2007,22(5):68-78.

[5] ZHANG L,LI C R,XU Y F,et al.An efficient solution to factor drifting problem in the pLSA model[C]∥Proceedings of 5th International Conference on Computer and Information Technology.Shanghai:IEEE,2005:175-181.

[6] GHARIBSHAH J,JALILI M.Connectedness of users-items networks and recommender systems[J].Applied Mathematics and Computation,2014,243:578-584.

[7] ZHANG Y C,BLATTNER M,YU Y K.Heat conduction process on community networks as a recommendation model[J].Physical Review Letters,2007,99(15):154301.

[8] ZHANG Y C,MEDO M,REN J,et al.Recommendation model based on opinion diffusion[J].Europhysics Letters,2007,80(6):68003.

[9] ZHOU T,KUSCSIK Z,LIU J G,et al.Solving the apparent diversity-accuracy dilemma of recommender systems[J].Proceedings of the National Academy of Sciences of the United States of America,2010,107(10):4511-4515.

[10] HUANG Z,CHEN H,ZENG D.Applying associative retrieval techniques to alleviate the sparsity problem in collaborative filtering[J].ACM Transactions on Information Systems,2004,22(1):116-142.

[11] NIE D C,AN Y H,DONG Q,et al.Information filtering via balanced diffusion on bipartite networks[J].Physica A:Statistical Mechanics and its Applications,2015,421:44-53.

[12] HE X S,ZHOU M Y,ZHUO Z,et al.Predicting online ratings based on the opinion spreading process[J].Physica A:Statistical Mechanics and its Applications,2015,436:658-664.

[13] GAN M X,JIANG R.ROUND:walking on an object-user heterogeneous network for personalized recommendations[J].Expert Systems with Applications,2015,42(22):8791-8804.

[14] HERLOCKER J L,KONSTAN J A,TERVEEN L G,et al.Evaluating collaborative filtering recommender systems[J].ACM Transactions on Information Systems,2004,22(1):5-53.

[15] GARDY J L,SPENCER C,WANG K,et al.PSORT-B:improving protein subcellular localization prediction for Gram-negative bacteria[J].Nucleic Acids Research,2003,31(13):3613-3617.

[16] LÜ L Y,MEDO M,YEUNG C H,et al.Recommender systems[J].Physics Reports,2012,519(1):1-49.

[17] HERLOCKER J,KONSTAN J A,RIEDL J.An empirical analysis of design choices in neighborhood-based collaborative filtering algorithms[J].Information Retrieval,2002,5(4):287-310.

(编辑:石 瑛)

Online-Rating Prediction Based on Opinion Spreading and an Improved Similarity Calculation Method

AI Jun, LI Linzhi, SU Zhan, WU Chunxue

(SchoolofOptical-ElectricalandComputerEngineering,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)

The relation between users and items in the recommendation system was considered as a complex network structure, and the binary relation between users and items was used to construct a graph model,based on which a diffusion dynamics method was introduced to study the recommendation algorithm.Through studying the ideas spreading in the network structure and collaborative filtering algorithms,two optimized algorithms were presented based on user similarity and item similarity,respectively.The proposed approach provides a correction method for zero value problems of similarity calculation,ignored in most existing publications.The similarity of users (or items) was defined as the number of corresponding views which a user (or items) owns and differences between those viewpoints spreading in the complex network.Using MovieLens data set,the experiments show that the presented algorithm has better performance than the collaborative filtering algorithm based on Pearson correlation coefficient and some other existing methods.

complexnetwork;recommendationsystem;ratingprediction;opinionspreading;similarity

1007-6735(2017)03-0236-05

10.13255/j.cnki.jusst.2017.03.006

2016-09-29

上海市自然科学基金资助项目(14ZR1428800;15ZR1428600)

艾均(1980-),男,讲师.研究方向:复杂网络.E-mail:aijun@outlook.com

TP 393

A