基于OpenFOAM的周期性管内流动边界处理方法研究
张 鹏, 凡凤仙
(1.上海理工大学 能源与动力工程学院,上海 200093;2.上海理工大学 上海市动力工程多相流动与传热重点实验室,上海 200093)
基于OpenFOAM的周期性管内流动边界处理方法研究
张 鹏1,2, 凡凤仙1,2
(1.上海理工大学 能源与动力工程学院,上海 200093;2.上海理工大学 上海市动力工程多相流动与传热重点实验室,上海 200093)
为探究开源计算流体力学软件OpenFOAM中不同周期性边界条件处理方法的适用性,针对圆管内泊肃叶流动,分别在mapped,cyclicAMI,cyclic fan边界条件下开展数值模拟,对模拟得到的速度分布和压力分布进行分析.结果表明:3种边界条件设置下,数值模拟得到的速度分布均与解析解吻合,其中mapped和cyclicAMI边界条件下的数值解非常接近,且与解析解吻合更好;采用mapped边界能够得到与解析解符合的压力场,采用cyclic fan边界时在模拟区域进、出口存在很大的压力梯度,采用cyclicAMI边界得到的压力则恒为0.基于此,探讨了mapped边界条件下,数值模拟结果对计算网格的敏感性.研究发现:随着径向网格数目的增加,速度的计算精度先迅速提高而后趋于稳定;边界层层数的增加能够有效提高近壁区速度的计算精度;数值模拟时径向网格数目采用 16个以上为宜,边界层层数不宜少于3层.
管内流动; 周期性边界条件; 泊肃叶流动; 计算流体力学; OpenFOAM
在工程实际应用中,不可压缩流体的管内流动非常普遍.随着计算机技术的快速发展,数值模拟技术在管内流动研究中得到了日益广泛的应用.数值模拟能够获得复杂流场的细节信息,从而成为研究流场内部流动结构的有力手段.能源、化工、制药、食品加工领域的管内物料输运通常是恒定压力梯度下的定常运动,且管道往往长达数十米以上.由于研究对象尺度很大,若对整个区域进行计算,工作量将非常大.在数值模拟中若能采用周期性边界条件,则可利用长度小很多(0.5~2 m)的管道代替实际管道,以减小模拟尺度,从而在不失精确度的前提下,大大降低计算量[1-3].如何施加周期性边界条件直接、有效地体现出管内周期性流动的所有特征,在目前的工程实际应用中具有重要的现实意义.
近年来,随着开源程序OpenFOAM的出现和发展,越来越多的科研和工程技术人员开始使用它进行计算流体力学(computational fluid dynamics,CFD)研究[4-6].OpenFOAM是一种基于C++语言的开源CFD程序库,它在本质上是一个预编译的功能库,用户可以通过命令调用这些功能库,也可以根据需要对这些功能库进行修改、继承,从而开发自己的CFD软件,以满足问题的需求[7].OpenFOAM因其免费、开源、稳定强大的底层类库,以及能够并行计算的优点受到广大CFD用户的青睐.由于边界条件的设置会影响数值计算结果的准确性,基于OpenFOAM对周期性管内流动进行高精度模拟,需要探讨不同周期性边界条件处理方法在OpenFOAM中的实现,并考量这些处理方法的适用性.管内泊肃叶流动作为一种典型的管内流动,因其有特定的解析解,常用于数值模拟中验证计算结果的准确性[8-10].为此,笔者以圆管内泊肃叶流动为研究对象,应用开源OpenFOAM软件,开展不同边界条件处理方法下周期性流动速度场与压力场的数值模拟,并将所得结果与解析解进行对比,以校验边界条件设置的适用性和准确性,为基于OpenFOAM系统研究周期性管内流动提供基础.
1 数学模型、边界条件设置及数值计算方法
1.1 数学模型

(1)
(3)
(4)
式中:ux为流体速度,m/s;ρ为流体密度,kg/m3;ν为流体运动黏度,m2/s;p为压力,Pa;t为时间,s.
1.2 边界条件设置方法
基于OpenFOAM模拟管内周期性泊肃叶流动可采用mapped,cyclicAMI和cyclic fan 3种边界类型,它们对应于不同的边界条件和初始条件设置.需要注意的是:OpenFOAM中的压力是以压力与流体密度之比的形式给出的,单位是m2/s2.
1.2.1 mapped边界
mapped边界的思想是从出口流出的流体以同样的速度从进口流入,从而形成周期性流动状态.本文模拟中,对应的边界条件设置见表1.
1.2.2 cyclicAMI边界
cyclicAMI边界通过对进口和出口的网格进行耦合,构建两者的联系,使流体的进口能够顺利地捕获出口的速度和压力信息.该边界条件的一个突出优点是即使进、出口网格数量不同,也能够实现网格的耦合.采用cyclicAMI边界时,边界条件设置见表2.此外,需要增加抽象基类选项文件“fvOptions”,并在该文件中设置流体速度场,平均速度Ubar设置为(0.01 0 0).
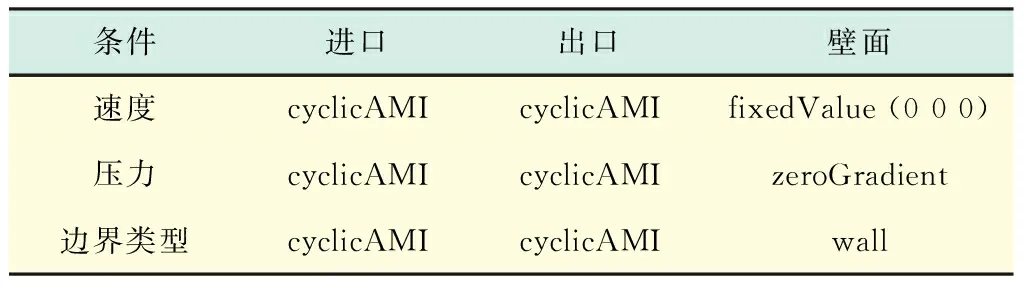
表2 cyclicAMI边界设置Tab.2 CyclicAMI boundary setup
1.2.3 cyclic fan边界
cyclic fan边界的基本思想是在进口设置虚拟风扇,利用风压对管内流体进行单向强力驱动,使流体流动并最终达到稳定状态.在进口为cyclic fan边界时,需要设置风压,OpenFOAM中风压由流体速度ux的n-1次n项式给出[7],即
(5)
在对进口风压进行设置时,采用“n-1 (A1A2A3…An)”的格式.据此,对于本文模拟,进口风压设置为“1 (0.0005 0)”.表3给出了具体的边界条件设置.
1.3 数值计算方法
OpenFOAM包含有适用于求解可压和不可压流体层流和湍流模型的多种算法.本文研究的泊肃叶流动为不可压缩流体的稳态流动,可采用SIMPLE算法[12]进行求解.求解流程为:a.在有限体积法的框架下,施加初始条件和边界条件;b.基于高斯二阶线性离散格式,求解动量方程,获得速度场;c.计算网格面的质量通量,进行亚松弛;d.求解压力方程,修正质量通量;e.在修正的压力场基础上,修正速度场;f.更新边界条件,重复上述步骤,直到满足收敛条件,计算结束.

表3 cyclic fan边界设置Tab.3 Cyclic fan boundary setup
2 结果与讨论
2.1 不同边界设置时数值模拟结果与解析解的对比
为验证数值模拟的准确性,本节将数值模拟结果与解析解进行对比分析.对于泊肃叶流动而言,流体速度在圆管的横截面上呈旋转抛物面分布,流体压力沿管长线性下降,它们的表达式分别为[13]
(6)
(7)
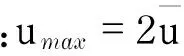
2.1.1 网格划分
运用OpenFOAM自有的网格生成程序block-Mesh与snappyHexMesh对圆管进行网格划分,如图1所示(见下页).其中,图1(a)给出了沿管长方向的网格划分,图1(b)给出了圆管出口段的网格情况,图(c)为圆管中心横截面的网格划分;计算区域总网格数目为126 400个.
2.1.2 速度场数值模拟结果与解析解的对比
3种周期性边界处理方法(mapped,cyclicAMI,

图1 圆管网格Fig.1 Cells on the circular pipe
cyclic fan)下得到的圆管中心截面直径AB(见图1(c))上的速度分布如图2所示.由图2(a)可知,在近壁面区域3种方法得到的数值模拟结果均与解析解吻合良好,而在中心区域数值解比解析解略小,并且数值解之间也有差异.为了清楚地展示中心区域的数值误差,对-0.3≤2z/d≤0.3对应的曲线进行局部放大,如图2(b)所示.可见,采用cyclicAMI和mapped边界条件处理方法所得到的数值解非常接近,且更接近于解析解,而采用cyclic fan边界与解析解的差异较前两种边界时略大.计算表明,3种周期性边界条件处理方法下数值模拟结果的相对误差在-4.4%~6.8%范围内,且相对误差上限和下限均出现在近壁区,这是由于近壁区速度的真实值(即解析解)接近0,较小的数值计算误差即引起相对误差绝对值的增大.
2.1.3 压力场数值模拟结果与解析解的对比
3种周期性边界处理方法下,数值模拟得到的沿管中心轴线的压力分布如图3所示.结果表明,3种方法下压力分布各不相同.mapped边界下,压力分布与解析解符合很好; cyclicAMI边界下,沿管中心轴线压力始终为零;cyclic fan边界下,压力在包含进口边界的网格内由Δp/2 (0.25 Pa)迅速上升至Δp(0.5 Pa),再由Δp线性减小至0,在包含出口边界的网格内迅速升至Δp/2 (0.25 Pa),表现为除进、出口边界网格内具有很大的压力梯度外,其余部分的压力分布和理论解吻合良好.本文是对单相流体的泊肃叶流动进行数值模拟,当将OpenFOAM用于周期性边界条件的两相流或多相流问题研究时,若需要考虑压力梯度力对颗粒的影响,则应当对压力进行准确预测,此时应采用mapped边界条件设置;若不需要考虑压力梯度力的影响,则可选用cyclicAMI和cyclic fan边界条件设置.考虑到cyclicAMI边界条件设置更为简便,且所得的速度场和解析解吻合更好,推荐采用cyclicAMI边界条件设置.
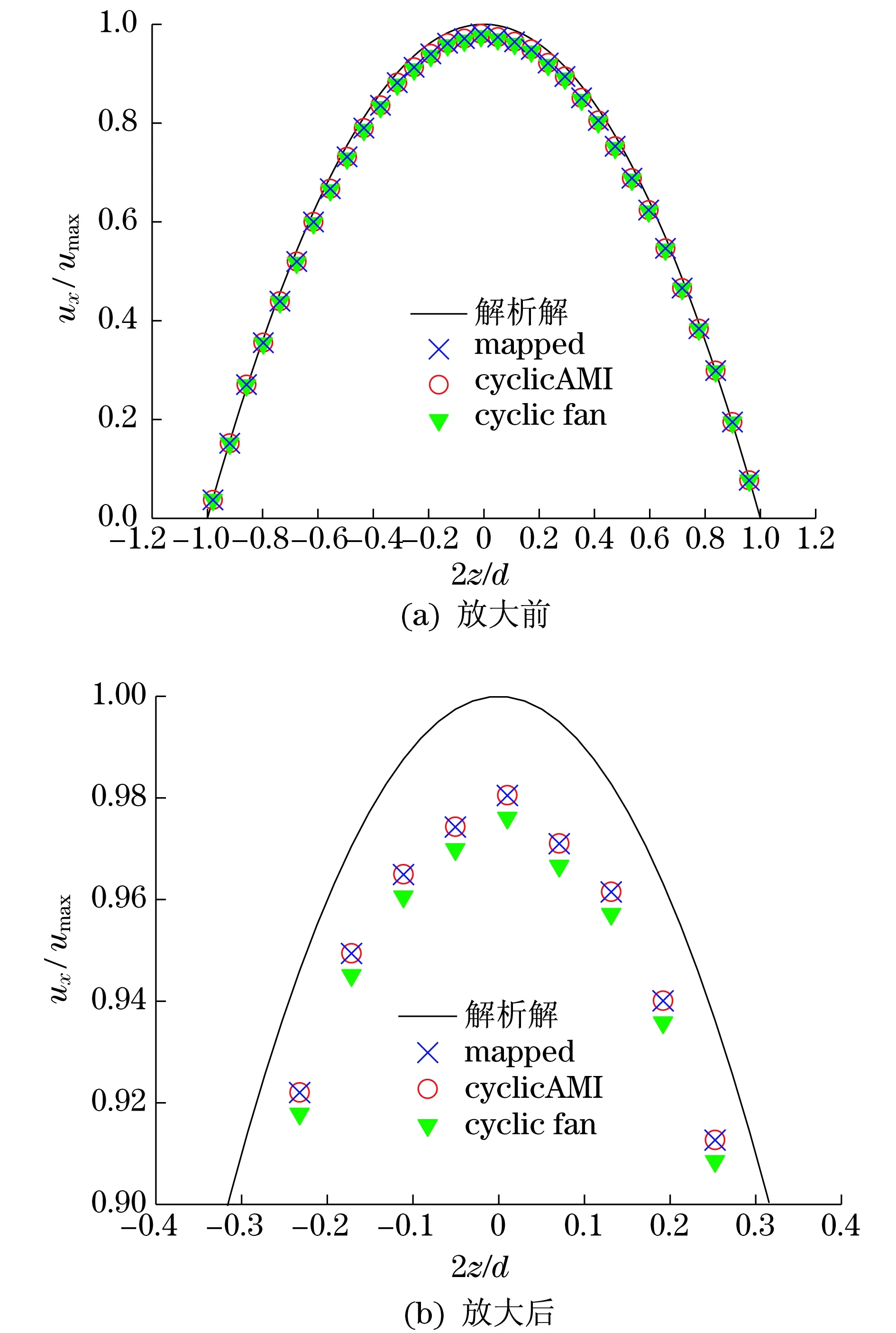
图2 3种周期性边界处理方法得到 的速度分布及与解析解的对比Fig.2 Velocity profiles obtained using the three periodic boundary implementation methods and their comparison with the analytical solution
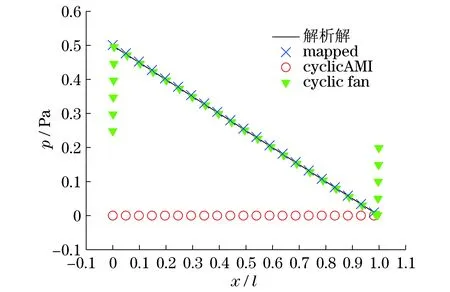
图3 3种周期性边界处理方法得到的 压力分布及与解析解的对比Fig.3 Pressure profiles obtained using three periodic boundary implementation methods and their comparison with analytical solution
2.2 网格划分对数值模拟结果的影响
以上数值模拟结果表明,与cyclicAMI,cyclic fan边界相比,mapped边界在模拟泊肃叶流动时,很好地实现了周期性泊肃叶流动的速度场和压力场特征,但其得到的速度场与解析解之间仍存在一定的偏差.在数值模拟过程中,计算结果与网格划分情况密切相关,因此本节在mapped边界条件设置下探究网格划分,如圆管径向网格数目和近壁面边界层层数对数值模拟结果的影响.
2.2.1 径向网格数目的影响
保持圆管轴向网格和近壁面边界层不变,改变横截面直径方向的网格数目,考察径向网格数目对于数值模拟结果的影响.用N表示径向网格数目,定义为不计边界层时沿截面直径方向的网格数目,图4给出了N=8,12,16,20,24时圆管中心截面网格情况.在N不同的情况下,数值模拟得到的圆管中心截面直径AB上的速度分布如图5(a)所示,对图5(a)中-0.4≤2z/d≤0.4对应的曲线进行局部放大,如图5(b)所示.可见,随着径向网格数目的增加,速度分布更接近于解析解.在N=8,12,16,20,24时,近壁区(2z/d<-0.8或2z/d>0.8)相对误差绝对值最大值分别为9.7%,6.8%,4.4%,3.1%,2.5%;其余区域(-0.8<2z/d<0.8)相对误差绝对值最大值则分别为7.3%,4.5%,2.2%,1.8%,1.6%.根据数值模拟结果,径向网格数目采用 16个以上为宜.

图4 不同径向网格数目下圆管中心截面网格划分Fig.4 Cells at the cross section of the circular pipe generated with different diametric cell numbers
2.2.2 边界层层数的影响
保持轴向网格划分和径向网格数目N=12不变,考察边界层层数对于数值模拟结果的影响.图6给出了边界层层数n分别为0,1,2,3时圆管中心截面的网格情况.在图6对应的边界层层数情况下进行数值模拟,得到的速度分布如图7(a)所示(见下页),对图7(a)中-0.4≤2z/d≤0.4对应的曲线进行局部放大,见图7(b)(见下页).对数值计算误差进行分析可知,虽然边界层层数越多,数值模拟所得到的速度场越接近解析解.然而边界层层数主要影响近壁区,而对其余区域的影响很弱.例如,n=0和n=1时,近壁区相对误差绝对值高达18.9%,而n=2和n=3时,近壁区相对误差绝对值分别为7.0%和4.4%.因此,为保证较高的计算精度,应在边界层层数不低于3的情况下进行数值模拟.
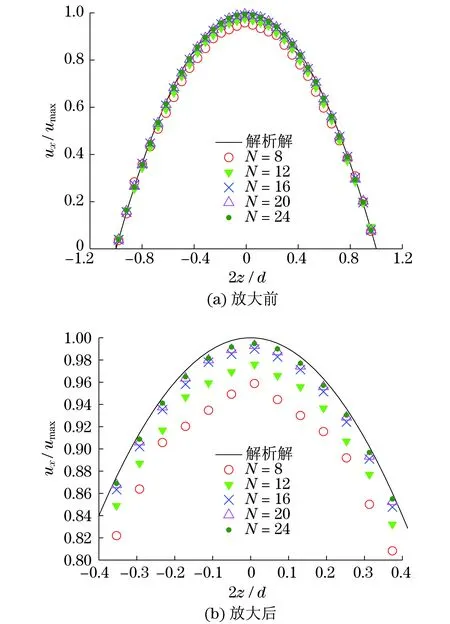
图5 不同径向网格数目下的速度分布Fig.5 Velocity profiles in cases with different diametric cell numbers
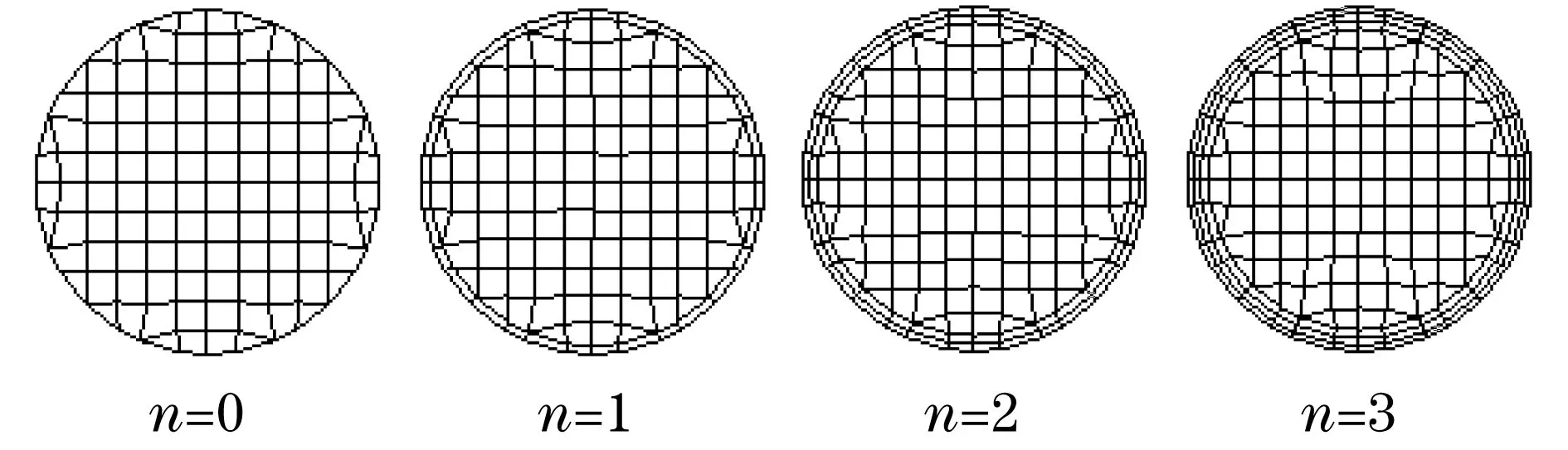
图6 不同边界层层数下圆管中心截面网格划分Fig.6 Cells at the cross section of the circular pipe generated with different boundary layers
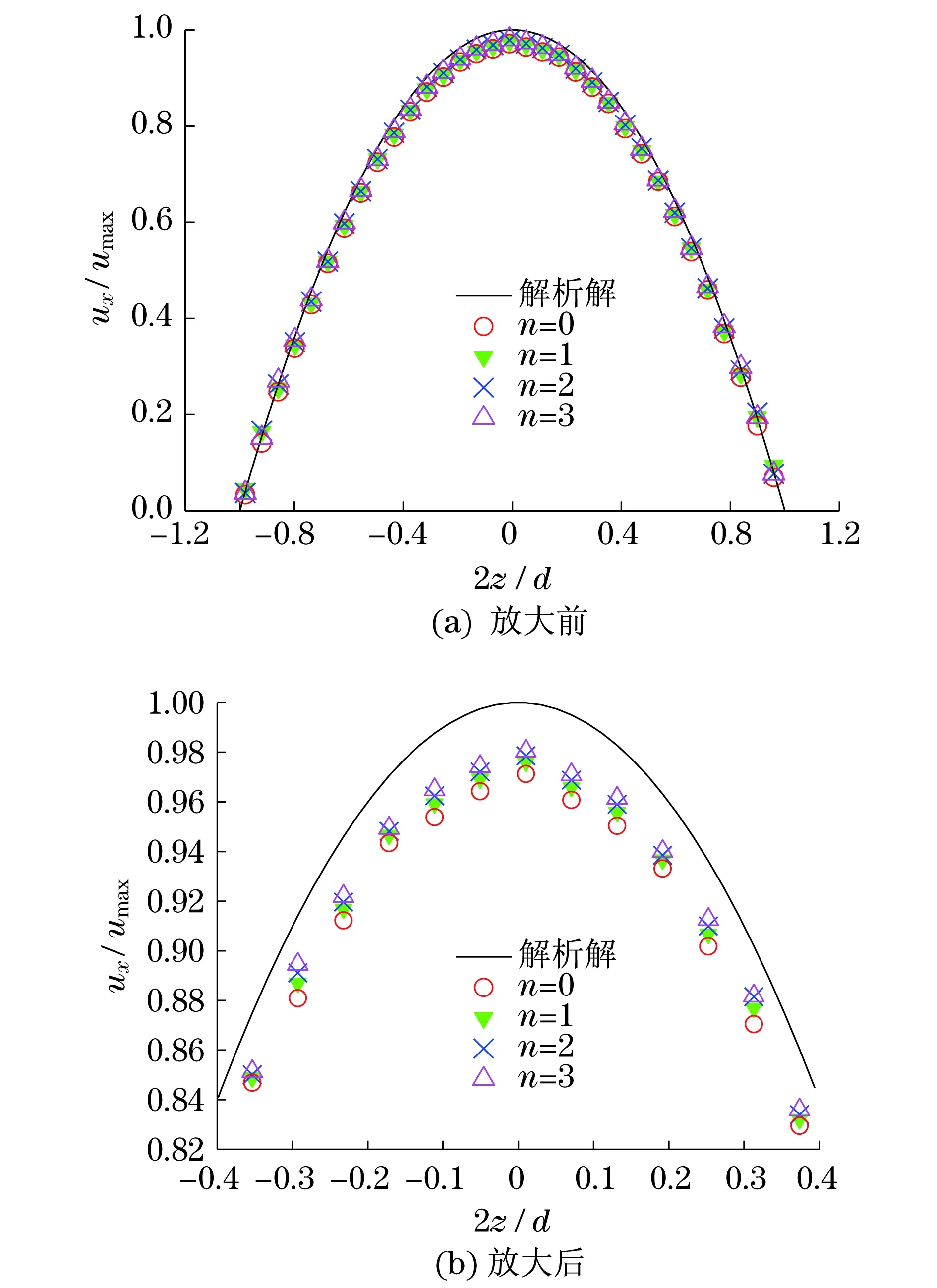
图7 不同边界层层数下的速度分布Fig.7 Velocity profiles in cases with different boundary layers
3 结论
利用开源CFD软件OpenFOAM对周期性管内单相流体的泊肃叶流动开展数值模拟,通过将OpenFOAM中3种周期性边界处理方法下的数值模拟结果与泊肃叶流动速度场和压力场的解析解进行对比,分析了3种周期性边界处理方法的适用性.在此基础上,考察了径向网格数目和边界层层数对速度场的影响.通过本文研究,得到以下结论:
a. 3种边界条件设置下,数值模拟得到的速度场均与解析解吻合,其中mapped和cyclicAMI边界条件下的数值解非常接近,且与解析解吻合更好.
b. 3种边界条件设置下,数值模拟得到的压力场差别很大.采用mapped边界时,压力与解析解十分接近;采用cyclic fan边界时,进、出口存在很大的压力梯度;而采用cyclicAMI边界时,压力则恒为0.
c. 在mapped边界条件下,随着径向网格数目的增加,速度的计算精度先迅速提高而后趋于稳定;边界层层数的增加能够有效提高近壁区速度的计算精度;数值模拟时径向网格数目采用 16个以上为宜,边界层层数不宜少于3层.
[1] KUANG S B,LI K,ZOU R P,et al.Application of periodic boundary conditions to CFD-DEM simulation of gas-solid flow in pneumatic conveying[J].Chemical Engineering Science,2013,93:214-228.
[2] YAN X K,HOLLOWAY W,SUNKARAN S.Periodic flow structures in vertical gas-particle flows[J].Powder Technology,2013,241:174-180.
[3] AROLLA S K,DESJARDINS O.Transport modeling of sedimenting particles in a turbulent pipe flow using Euler-Lagrange large eddy simulation[J].International Journal of Multiphase Flow,2015,75:1-11.
[4] JACOBSEN N G,FUHRMAN D R,FREDSØE J.A wave generation toolbox for the open-source CFD library:OpenFOAM®[J].International Journal for Numerical Methods in Fluids,2012,70(9):1073-1088.
[5] 陈存杨,朱勇兵,陈崇成,等.基于OpenFOAM的城市街区毒气扩散模拟[J].环境科学研究,2015,28(5):697-703.
[6] 刘秀丽,段梦兰,高攀,等.基于OpenFOAM的数值波浪水槽研究[J].复旦学报(自然科学版),2015,54(3):373-378,385.
[7] OpenFOAM Documentation.OpenFOAM User Guide Version 2.3.1[DB/OL].[2015-11-15].http:∥www.openfoam.org/docs/.
[8] BAYAREH M,MORTAZAVI S.Equilibrium position of a buoyant drop in Couette and Poiseuille flows at finite Reynolds numbers[J].Journal of Mechanics,2013,29(1):53-58.
[9] PAZOUKI A,NEGRUT D.A numerical study of the effect of particle properties on the radial distribution of suspensions in pipe flow[J].Computers & Fluids,2015,108:1-12.
[10] QIU X,WANG H F,LUO J P,et al.Characteristics of velocity gradient jumping discontinuity in steady Poiseuille flow of Johnson-Segalman fluid[J].International Journal of Non-Linear Mechanics,2015,71:72-82.
[11] 林建忠,包福兵,张凯,等.微纳流动理论及应用[M].北京:科学出版社,2010.
[12] VAISH M.Lung-aerosol dynamics in human airway models:validation and application of OpenFOAM software[D].Raleigh,USA:North Carolina State University,2014.
[13] 归柯庭,汪军,王秋颖.工程流体力学[M].北京:科学出版社,2003.
(编辑:丁红艺)
Implementation of Boundary Conditions for Periodic Pipe Flow Based on OpenFOAM
ZHANG Peng1,2, FAN Fengxian1,2
(1.SchoolofEnergyandPowerEngineering,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China;2.ShanghaiKeyLaboratoryofMultiphaseFlowandHeatTransferinPowerEngineering,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)
In order to explore the applicability of different implementation methods for periodic boundary conditions involved in the open-source computational fluid dynamics software,by the name of OpenFOAM,numerical simulations on the Poiseuille flow in a circular pipe were performed,using mapped,cyclicAMI and cyclic fan boundary conditions,respectively.The numerically obtained velocity and pressure profiles were analyzed.The results show that the velocity profiles obtained under the three boundary conditions are in agreement with the analytical solution.Specifically,the results under the mapped and cyclicAMI boundary conditions,which are very close to each other,agree better with the analytical solution.The pressure profile obtained under the mapped boundary condition is in good agreement with the analytical solution,whereas there are large pressure gradients at the inlet and outlet of the simulation domain when the cyclic fan boundary condition is adopted.Moreover,the pressure along the pipe axis is always zero under the cyclicAMI boundary condition.On this basis,the sensitivity of the numerical simulation results to the computational cell was examined.It is found that as the cell number along the pipe diameter increases,the computational accuracy of the velocity increases rapidly and then becomes stable.The increase of the number of boundary layers can effectively improve the computational accuracy of the velocity near the wall.Furthermore,more than 16 cells along the diameter and not less than 3 boundary layers are necessary for numerical simulations.
pipeflow;periodicboundarycondition;Poiseuilleflow;computationalfluiddynamics(CFD);OpenFOAM
1007-6735(2017)03-0217-06
10.13255/j.cnki.jusst.2017.03.003
2016-07-12
国家自然科学基金资助项目(51206113,51176128,51576130);上海市科委科研计划(13DZ2260900)
张 鹏(1992-),男,硕士研究生.研究方向:多相流数值模拟.E-mail:zippousst@126.com
凡凤仙(1982-),女,副教授.研究方向:多相流动与传热.E-mail:fanfengxian@hotmail.com
O 351
A

