基于蝙蝠算法的电气化铁路电能质量控制系统容量配置
吴玉龙,徐 龙,李胜文
(1.太原理工大学,山西 太原 030024;2.国网山西省电力公司电力科学研究院,山西 太原 030001)
·电网技术·
基于蝙蝠算法的电气化铁路电能质量控制系统容量配置
吴玉龙1,徐 龙2,李胜文2
(1.太原理工大学,山西 太原 030024;2.国网山西省电力公司电力科学研究院,山西 太原 030001)
在研究和解决电气化铁路的负序和谐波问题的过程中,针对基于V/V变压器的铁路电能质量控制系统的优化模型,采用蝙蝠算法计算补偿系数的全局最优解和补偿容量的目标最小值。算例表明,采用该算法能够在全局范围内满足电能质量指标的同时减少补偿容量进而提高电气化铁路运行时的经济性。
电气化铁路;V/V变压器;电能质量;蝙蝠算法
0 引言
近年来,因具有高速化、能源利用率高等特点,电气化铁路在我国迅速发展。电力机车从公用电网中获取电能的同时会给其注入谐波和负序电流,使得电力系统存在谐波和三相不平衡等电能质量问题,对电网的安全经济运行产生影响[1]。目前,处理这些问题常用的措施是安装合适的补偿装置[2]。其中一位日本学者提出的铁路静止功率补偿器,亦称为铁路电能质量控制系统RPQMS (railway power quality manage system),能够对电气化铁路牵引供电系统中所存在的谐波、负序等问题做出综合处理,故该系统在电气化铁路的发展中具有比较好的应用前景[3]。由于RPQMS由全控器件——绝缘栅双极型晶体管IGBT (insulatedgate bipolar transistor)构成,如果在不进行容量优化的情况下使用该系统,则经济成本太高。所以,优化补偿容量对于RPQMS的发展是极为重要的。
目前,常用的容量优化方法大多数只是考虑了电能质量指标与补偿系数之间的关系。文献 [4]使用傅里叶变换对系统进行频谱分析,然后根据对数据的分析结果来搜寻储能系统所需补偿容量的最优解。文献 [5]求解了基于无功优先的负序补偿的最优解,但是该文并未考虑到负序优先的情况。文献 [6]基于以上所述问题进一步考虑了电能质量指标与补偿系数和负载特性的关系,并建立了以RPQMS的拓扑结构为依据所推导出的容量优化模型。本文是在文献 [6]所建立的模型的基础上进一步采用更好的算法——蝙蝠算法BA (bat algorithm)[7]来求取补偿系数的全局最优解。
1 电气化铁路的电能质量分析
1.1 牵引负荷引起的电能质量特性
1.1.1 负序特性
目前,我国所使用的牵引负荷多为线性的单相交流负荷,所以公用电网首先需要将三相电经过牵引变压器转化为单相电,然后再供给牵引负荷,于此同时牵引负荷在从电网获得电能的时候会给其注入负序电流,从而引起公用电网的三相不平衡。
1.1.2 谐波特性
因电力机车多采用一定量的电力电子设备,故其存在波动性、不对称性等特点,在运行的过程中会产生谐波并将其注入电网;且该谐波含有幅值随机波动、相位分布广泛等特点。目前,我国使用的电力机车产生的谐波含量主要以3次、5次、7次等基次谐波为主[2]。
1.1.3 功率因数特性
整流型电力机车为我国使用最多的牵引负荷,由于负序、谐波等问题会使得交流侧的电流波形产生畸变,而且在整流的换相过程中会产生换相重叠角,这些问题会使得电气化铁路在使用过程中功率因数偏低,一般为0.8~0.85。
1.2 负序和谐波的治理
负序、谐波问题会对电网中的电机、变压器、输电线路以及继电保护和自动装置等产生影响,为此需要对其进行控制或治理。目前常用的解决此类问题的措施之一即为安装合适的容量优化装置。
2 RPQMS容量优化模型
2.1 RPQMS的拓扑结构及其相量图
如图1和图2所示,分别为基于V/V变压器的铁路电能质量控制系统的优化模型系统[6]V/ V—RPQMS(V/V—railwayowerqualitymanage system)的拓扑结构图及该系统中补偿前后电流、电压的相量关系图。图2中的ΔIp表示变压器二次侧两相之间转移的基波有功电流分量。图1,2中,L1、L2、L3表示三相线路,下标A、B、C分别表示L1、L2、L3三相对应的物理量,下标a1、a2分别表示变压器T1、T2的二次侧,下标L和c分别表示负载量和补偿量,下标p、q分别表示其有功分量和无功分量。
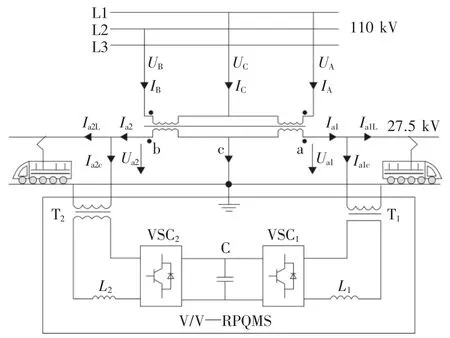
图1 V/V—RPQMS系统结构
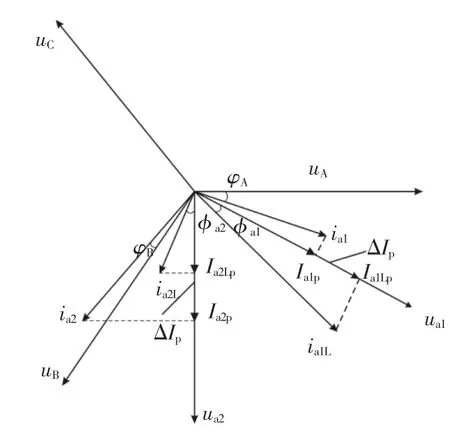
图2 V/V—RPQMS系统相量
2.2 容量优化补偿
容量优化补偿是指在能够满足电能质量基本指标的前提下,实现所需的补偿容量最小。
2.2.1 基波优化补偿
根据戴维南定理,见图1和图2所示相量关系,可得变压器二次侧a1、a2相基波补偿电流,见式(1)。
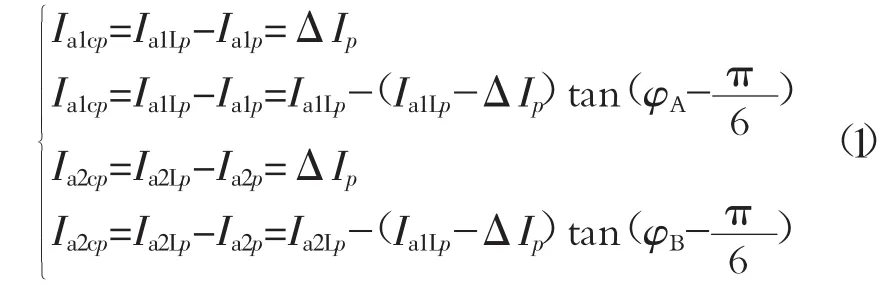
基波补偿功率见式(2)。
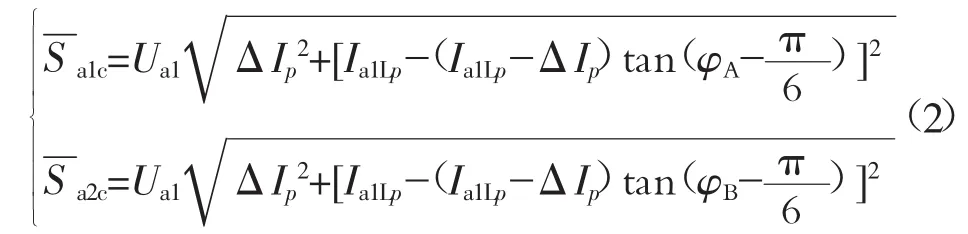
则总的基波补偿功率见(3)。

2.2.2 谐波优化补偿
类比基波优化补偿,谐波优化补偿需要的补偿功率见式(4)。
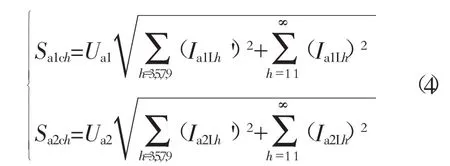
其中,Ia1Lh、Ia2Lh和Ia1Lh'和Ia2Lh'分别为变压器二次侧a1、a2相牵引负荷产生的补偿前后的各次谐波电流。
由此可得总的谐波补偿功率见(5)。

则由式(3)和式(5)可得RPQMS系统总的补偿功率,见式(6)。

由此选择ΔIp、φA和φB作为RPQMS的容量优化补偿系数。
2.3 电能质量与负载特性的关系
2.3.1 负序电流与电压不平衡度负序电流与电压不平衡度的关系见式(7)。
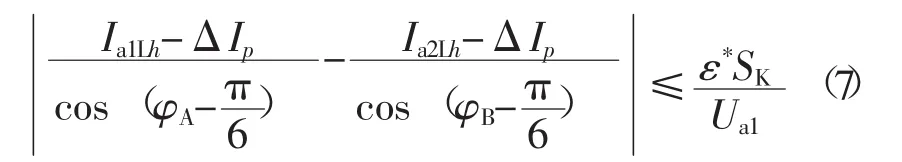
其中,ε*为电压不平衡度给定值,SK为公共连接点三相短路容量(MVA);且0≤φA≤π/6,0≤φB≤π/6。
2.3.2 功率因数
审计质量无法直观观测,从目前的研究结果来看,有以下审计质量的替代指标,但单独指标具有局限性,需要多个指标互相支撑印证来评价审计质量的高低。
设牵引网高压计量点处三相功率因数为PF,如果要使得PF≥PF*(PF*为功率因数给定值)成立,则需满足式(8)约束。
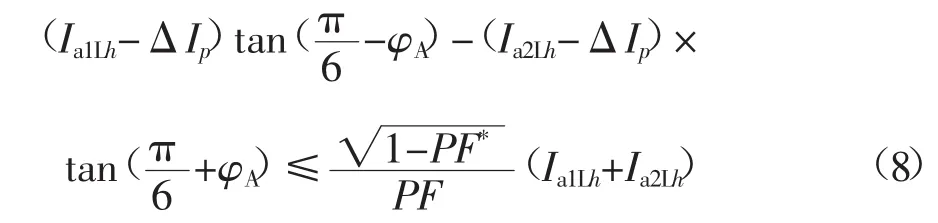
2.4 RPQMS容量优化模型
建立如下所示以ΔIp、φA和φB为决策变量的RPQMS容量优化数学模型[6]。

可看到该模型为一个复杂的非线性规划问题,本文将采用BA算法来对该问题进行求解。
3 BA算法
3.1 BA算法基本原理简述
自然界中的蝙蝠基本上都是依靠回声定位的原理来确定其所要捕食的猎物所在的方位。蝙蝠狩猎的过程可以等效为在所有解的集合内寻找满足约束条件的最优解的过程,数学描述即为式(9)、式(10)、式(11)所示,即“蝙蝠”算法[8]。设所有“蝙蝠”所形成的种群为m,且“蝙蝠”在一个n维空间里,有
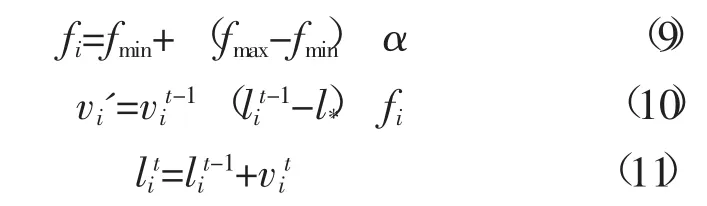
其中,α是在 [0,1]之间的一个随机数,vi'表示“蝙蝠”i在t时刻的速度,lit是指“蝙蝠”i在t时刻所处的位置,l*是取到最优解时“蝙蝠”i所处的位置, fi为“蝙蝠”i所发出的声波的频率,其中每只“蝙蝠”得频率都是在初始化的时候由算法随机分配的,同时所分配的频率的取值都要满足给频率所设定的范围。
在该算法进行局部搜索的过程中,如果所选择的解为最优解集合的一个解,那么该“蝙蝠”此时所处的位置则要按照式(12)来重新进行确定。

“蝙蝠”寻找“猎物”时,它所发出的脉冲的响度Ai和频度Pi不是固定的,而是一直变化的,由式(13)和式(14)来计算。
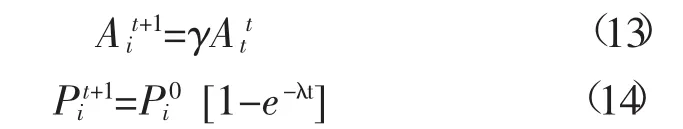
其中,γ为脉冲响度增加系数,在 [0,1]之间。λ为脉冲频度衰减系数,是一个大于零的数。这两个系数的取值取决于要研究的实验对象。
在BA算法中,所构造的目标函数的最优解就相当于“蝙蝠”i所搜寻到的猎物;而Ai和Pi的变化则可以用来说明搜寻到的猎物与最优解的临近程度。
3.2 BA算法求解非线性规划问题
如果将容量优化补偿的过程转化到以上所述的BA算法中,实质上就是对n维空间内的“蝙蝠”种群在满足约束条件的基础下进行优化求解。
“蝙蝠”的位置可以由变压器二次侧的某两相之间所转移的基波有功电流分量ΔIp来表示。该算法每次迭代的过程中都要将所搜寻到的“蝙蝠”的当前所处位置用所构造出的目标函数来评价其优劣性,并且根据评价结果更新“蝙蝠”在当前时刻下的速度和位置,直到满足所设定的结束条件为止。最后所得到的“蝙蝠”位置即为所搜寻的最优解。具体的算法流程图如图3所示。其中i的位置初始化为n行1列的数列,N为设定的算法迭代最大值,count为目标最小值Fmin重复出现的次数。又因本文将“蝙蝠”的Ai和Pi都设为定值,所以不需要对γ和λ进行初始化。
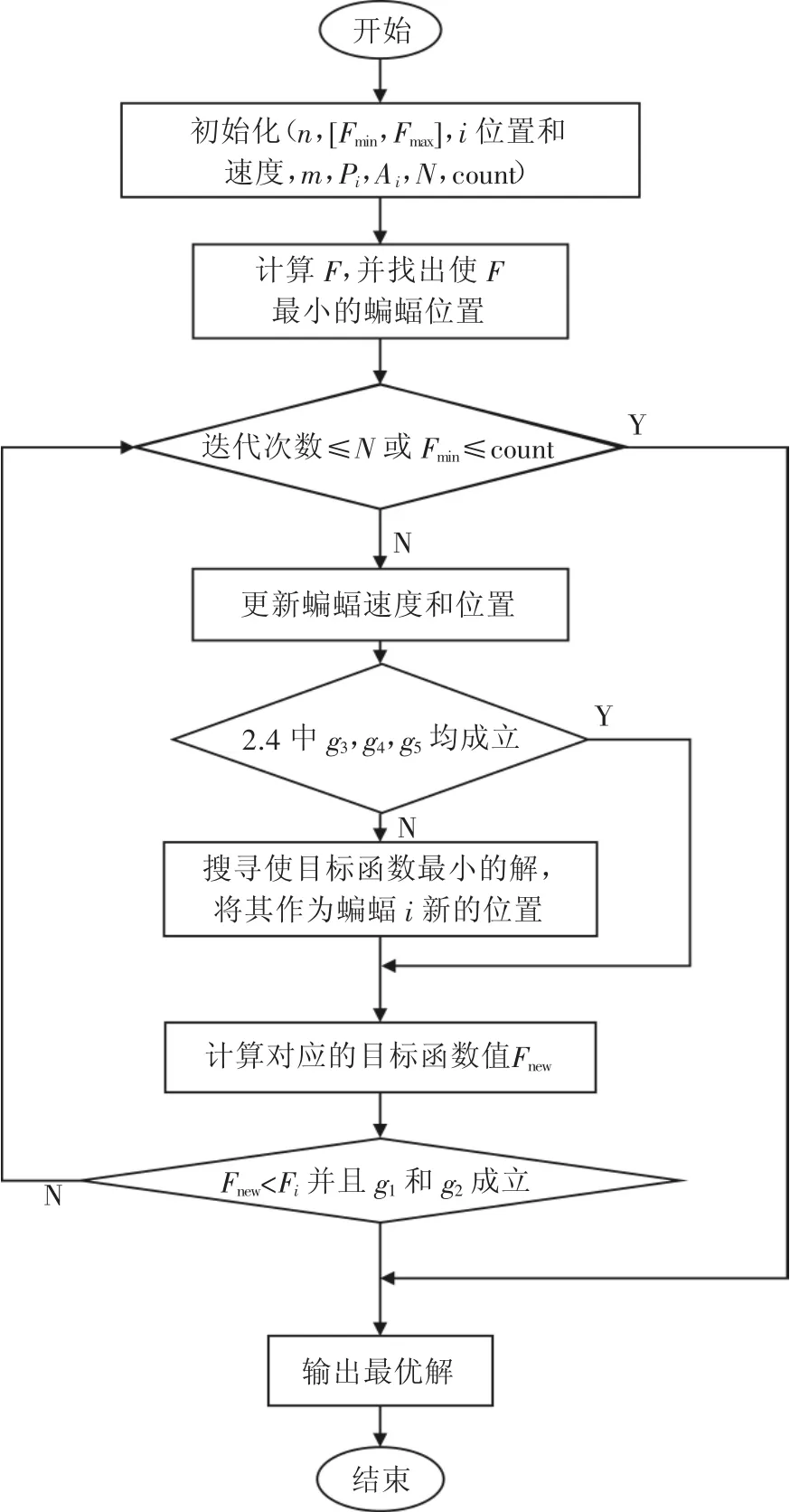
图3 BA算法求解优化模型流程图
4 算例分析
4.1 实验结果
对V/V—RPQMS系统,在考虑电能质量指标的前提下,采用BA算法,对接不同负载的系统进行优化计算,其中负载分别接为a1相取最大负载,a2相空载;a2相负荷大于a1相负荷且a2相负载电流ia2L滞后于uB的情况;a1相空载,a2相取最大负载。其中系统的各参数分别为:系统短路容量为450 MVA;变压器连接组标号为VV0/ VV6;变压器额定容量:AC绕组为6 000 MVA,BC绕组为10 000 MVA;变压器电压比为110(1±5%)/ 27.5;RPQMS容量为8 500×2 kVA;串联等效电阻为0.2 Ω,串联等效电抗为70 mH,直流电压为85 kV;直流电容为6 000 μF;开关频率为1 900 Hz。如表1所示即为在3种不同负载下所得到的补偿系数的最优解以及补偿容量最小值。
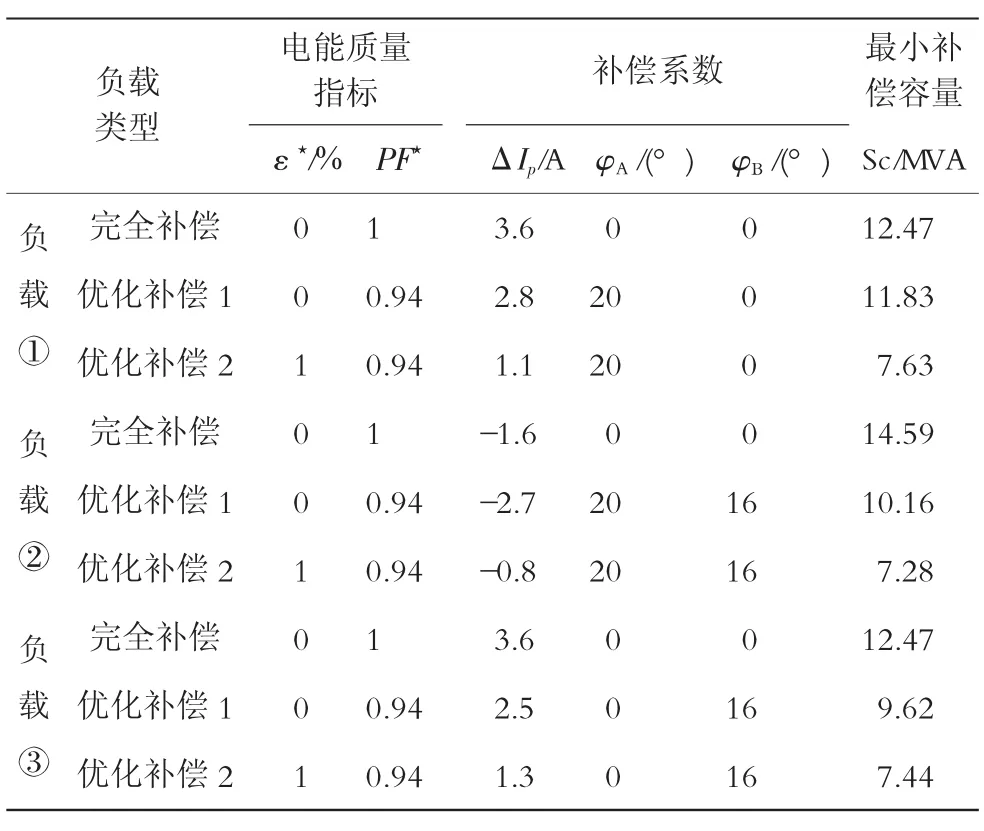
表1 算例计算结果
4.2 数据分析
表1中,系统接入3种不同负载时,包括负载①、负载②和负载③,计算得出优化结果,每种负载的第1行,完全补偿时的数据;第2行优化补偿1,电能质量指标只考虑功率因数而不考虑电压不平衡度时求得的补偿系数的最优解和RPQMS最小补偿容量的数据;第3行优化补偿2,同时考虑了两个电能质量指标——功率因数和电压不平衡度时所求得的补偿系数的最优解和RPQMS最小补偿容量的数据。
负载②在做优化补偿计算的时候其补偿系数的最优解φB=16°,不再是负载①中所计算出的φB=0°。根本原因在于此时变压器二次侧a2相的ia2L滞后于uB,所以将ia2L补偿到φB=16°所需无功功率较少。
同理,在所接负载为负载③的情况下,可以看到补偿系数的最优解为φA=0°,φB=16°,其原因在于变压器二次侧a1相的负载电流ia1Lp滞后于电压uA,而a2相的负载电流ia2L则超前于电压uB,所以将ia1L补偿到与uA同相(即φB=0°) 所需无功功率比将ia1L补偿到比uA超前所需的无功功率较少。
以上算例表明,采用蝙蝠算法对 V/V—RPQMS系统做容量优化补偿,与完全补偿进行对比,可以在满足基本电能质量指标的前提下,获得全局范围内的补偿系数的最优解,并且减少所需最小补偿容量,比完全补偿具有更好的电力系统运行经济效益,使得V/V—RPQMS系统可以获得更好的应用价值。
4.3 结论
利用蝙蝠算法对基于V/V变压器的电气化铁路控制系统做容量优化计算,能够在控制电能质量指标满足要求的基础上,获得全局范围内补偿系数的最优解和最小补偿容量。比较系统中接入不同负载时的最优补偿系数以及最小补偿容量,可以判断出不同负载时的最优补偿系数和最小补偿容量的值是不同的;但是相比较于全部补偿,利用蝙蝠算法计算出的补偿容量都小于全部补偿所需的最小补偿容量。利用蝙蝠算法可以显著减少电气化铁路控制系统所需的最小补偿容量,进一步提高电气化铁路运行的经济效益。
[1]于坤山.电气化铁路供电与电能质量 [M].北京:中国电力出版社,2011:15-65.
[2]王金浩,徐龙,冯磊,等.电气化铁路电能质量问题分析[J].电力与能源进展,2016,4(1):1-8.
[3]胡斯佳,张志文,李勇,等.一种绕组补偿式电气化铁道电能质量控制系统 [J].中国电机工程学报,2014,34(13):2140-2150.
[4]王成山,于波,肖峻,等.平滑微电网联络线功率波动的储能系统容量优化方法 [J].电力系统自动化,2013,37(3):12-17.
[5]魏应冬,姜齐荣,韩英铎,等.基于无功与负序对称解耦的RUPQC最优补偿策略 [J].电力系统自动化,2009,33 (16):55-60.
[6]罗培,陈跃辉,罗隆福,等.铁路电能质量控制系统容量优化设计 [J].电工技术学报,2016(8):181-188.
[7]Yang X S.A New Metaheuristic Bat-Inspired Algorithm[J]. Computer Knowledge&Technology,2010(284):65-74.
[8]付家才,陆青松.基于蝙蝠算法的配电网故障区间定位[J].电力系统保护与控制,2015(16):100-105.
Capacity Configuration of Electrified Railway Power Quality Control System Based on Bat Algorithm
WU Yulong1,XU Long2,LI Shengwen2
(1.Taiyuan University of Technology,Taiyuan,Shanxi030024,China; 2.State Grid Shanxi Electric Power Research Institute of SEPC,Taiyuan,Shanxi030001,China)
In the process of researching and achieving a better realization of the negative sequence and harmonic wave problems of electrified railway,the optimization model of railway power quality manage systembased on V/V transformer is optimized in this paper.The bat algorithm is used to calculate the global optimal solution of the compensation coefficient and the minimum value of the compensation capacity.The experimental results showthat the method can reach optimal compensation effect as well as the power quality index in the whole load range,which significantly improves the economic performance of RPQMS(railway power quality manage system).
electrified railway;V/V transformer;power quality;bat algorithm
TM71
A
1671-0320(2017)03-0001-05
2016-12-11,
2017-04-13
吴玉龙(1988),男,山西太原人,2010年毕业于浙江海洋学院电气工程及其自动化专业,助理工程师,从事电能质量以及新能源发电技术等研究工作;徐 龙(1985),男,山西翼城人,2011年毕业于北京交通大学电气工程专业,硕士,工程师,从事电能质量、新能源发电等研究工作;
李胜文(1986),男,山西朔州人,2013年毕业于天津大学电气工程专业,硕士,工程师,主要研究方向为电力系统电能质量分析与控制、新能源发电及智能电网技术。

