D-vine copulas混合模型及其在故障检测中的应用

郑文静，李绍军，蒋达

（华东理工大学化工过程先进控制和优化技术教育部重点实验室，上海 200237）

D-vine copulas混合模型及其在故障检测中的应用

郑文静，李绍军，蒋达

（华东理工大学化工过程先进控制和优化技术教育部重点实验室，上海 200237）

过程监控技术是保证现代流程工业安全平稳运行及产品质量的有效手段。传统的过程监控方法大多采用维度约简方法提取数据特征，且要求过程数据必须服从高斯分布、线性等限制条件，对复杂工况条件下发生的故障难以取得较好的检测效果。因此，提出了混合D-vine copulas故障诊断模型，在不降维的情况下直接刻画数据中存在的复杂相关关系，构建过程变量的统计模型实现对存在非线性与非高斯性过程的精确描述。通过EM算法和伪极大似然估计优化混合模型参数，然后结合高密度区域（HDR）与密度分位数法等理论，构建广义贝叶斯概率（GBIP）指标实现对过程的实时监测。数值例子及在TE过程上的仿真结果说明了该混合模型的有效性及在故障检测中的良好性能。

过程监控；非线性非高斯；相关性分析；D-vine copulas

引 言

化工过程行业日益增多的安全事故使人们关注的焦点转向了研究如何保证生产过程的安全性、可持续性和稳定性上。实时的过程监控是保证工业过程安全平稳运行以及产品质量的关键技术和有效手段[1]。随着实时数据采集系统及数据处理技术在流程工业中的广泛应用，基于数据驱动的过程监控技术也得到迅速发展。其中，多变量统计过程监测方法（multivariate statistical process monitoring，MSPM）利用多元投影技术将高维数据空间投影到低维的特征空间，提取数据特征进行统计建模实现对过程的监测，已成为过程监控领域的研究热点[2]。此类算法通常假定过程变量之间是线性相关的且变量均服从高斯分布。然而实际过程比模型假设更为复杂，对于存在非线性、非高斯特性的工业过程难以取得较好的监测效果。针对如何处理这些约束问题，许多新的过程监控方法也相继提出，如基于神经网络的非线主元分析（principal component analysis，PCA）方法[3]、基于支持向量机的核PCA（kernel principal component analysis，KPCA）方法[4]用来解决非线性问题，Cai等[5]提出的基于鲁棒独立成分分析（independent component analysis，ICA）方法通过稳健白化算法提取非高斯特征、Ge等[6]研究的基于 ICA-PCA两步信息提取策略的过程监测方法来处理非高斯问题。然而降维或去耦合过程仍是MSPM的主要思想。尽管这些改进方法在不同程度上提升了监测效果，但降维的过程必定会带来信息损失。在不降维的情况下直接利用数据的分布信息刻画数据存在的复杂相关性行为，构建数据的分布模型进行过程监测具有很大的发展潜力。

近年来，copula作为一种用于描述复杂随机变量之间的相关性的有效统计工具，越来越广泛应用在经济、金融和气象学中，甚至化工过程系统中[7-9]。而传统多元 copula（如多元正态 copula、多元t-copula、多元Archimedean copula等）理论因其繁琐、低效的优化过程目前很少应用在过程监测领域。1996年，Joe[10]提出了vine结构来分析不同的相关性结构，将多元copula分解成若干个二元copula的组合形式，高维变量的相关性优化问题则相应地转化成一系列二元copula的参数优化问题，极大地降低了计算复杂度。有限元混合模型由于其较强的灵活性广泛用于复杂多元数据的统计建模中，出现了将copula理论与有限元混合模型结合并应用在模式识别、机器学习、数据挖掘等领域[11-13]。例如，Nguyen等[14]建立了 Clayton、Frank、Gumbel和 Joe copulas的混合模型用于捕获股票市场和黄金价格之间的相关信息，以优化组合投资和风险评估。Nikoloulopoulos等[15]提出有限正态混合copulas的多元离散数据建模并详细分析了混合模型的优良性质。

本研究提出了D-vine copulas混合模型，对多维数据的内在相关结构进行分析，选择典型的D-vine copula进行建模。将D-vine copula与有限元混合模型相结合，不仅能更全面挖掘随机变量间不同的相关性结构，而且为统计建模赋予了更强的灵活性。针对复杂工业过程数据建立 D-vine copulas混合模型，并结合高密度区域（HDR）与密度分位数法等理论，构建了广义贝叶斯推断概率（GBIP）指标[16]，通过查询静态密度分位数表对混合模型下存在非线性、非高斯特性的故障数据进行故障检测。在数值例子及TE过程中的应用，表明该混合模型在过程监控中有较好的检测效果。

1 D-vine copula

copula理论最早是由Sklar[17]于1959年提出的一种用于描述变量之间相关性的统计理论。根据Sklar定理，copu la是以服从均匀分布U[0, 1]的边缘分布函数为自变量而构成的多元分布函数，将联合分布函数用各变量的边缘分布函数和其相关性结构（即 copula函数）进行替代。对于 d维随机变量其联合分布函数可以表示为[18]

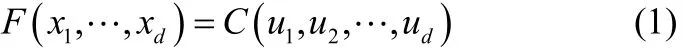
ui是第i个变量的边缘累积分布函数，满足

其中，fi(xi)为第i个变量xi的边缘概率密度函数。C表示多元copula函数，若各个变量的边缘累积分布函数连续，那么有唯一一个copula函数与其相对应。如果C可微，则各随机变量相对应的联合概率密度函数（probability distribution function，PDF）

式（3）中的密度函数c定义为

一旦copula的结构和参数确定，多维数据的联合密度分布函数就可以通过式（3）获得。显然，随着变量维数的增加，利用样本数据拟合式（4）的求解过程会变得更加困难，造成传统多元copula计算量增加的问题。

1.1 二元copula结构

在copula族中，用于刻画二元随机变量相关性结构的二元 copula是最为常见也最为简单的一类copula，其优化过程是一个易于实现的问题。vine copula模型可将一个多元联合分布分解成多个二元copula函数和各个变量边缘分布的组合形式。此时高维变量的相关性优化问题则相应地转化成一系列二元 copula的参数估计问题。对于 d维随机向量其PDF可以分解成如下形式

进一步分解式（5）中的条件分布[19]，有

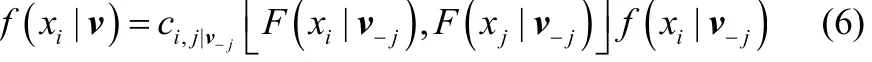
其中，v=x-i表示不包括变量xi的d-1维向量，vj为向量v中的任意一个元素，v-j为v去掉元素vj后所得的向量，ci,j|v-j为对应的条件二元copula密度。

常见的二元copula有Elliptical族（包括Gaussian、Student-t等二元copula）与Archimedean族（包括Clayton、Gumbel、Frank 等二元 copula）[20]。

1.2 D-vine copula

采用D-vine copula来描述d个变量之间相关性时，该相关性模型由d-1棵树组成每棵树由节点和连接节点的边组成，T1树上的节点表示变量，边表示变量之间的相关关系，即二元copula对。第1棵树以外的其他节点选自于上一棵树的对应边，整个模型共包含d(d-1)/2个二元copula函数。D-vine copula结构的联合密度函数的表达式为

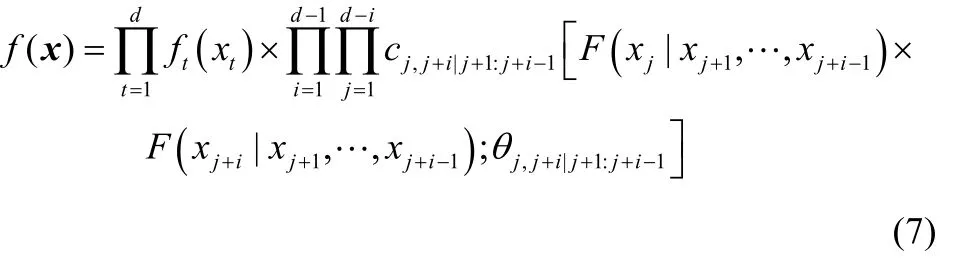
其中，θ表示相对应的copula参数。与式(3)相比，d维copula密度函数即转化为式（7）中个二元copula（即）相乘的形式，避免了式（4）中的多次求导过程。

式（7）中的二元copula包含了条件分布函数，如何分析这些条件分布函数直接关系到模型的可实现性。Aas等[21]提出了计算上述条件分布函数的 h函数，具体表达形式如下

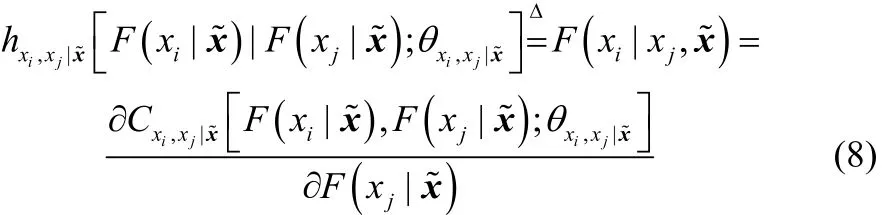
D-vine copula中一系列的条件分布函数均是基于式(8)迭代计算获得。

为了便于理解，以四维变量为例，图1展示了D-vine copula的结构分解图。如图所示，四维D-vine copula的分解结构有3棵树，树Tj由5-j个节点和4-j条边组成，每条边代表一个二元copula函数，整个D-vine结构共需要确定6个二元copula函数。树Tj是在树Tj-1的基础上确定的，树T1的节点和边确定之后才能确定树T2，然后再往下逐层推导。

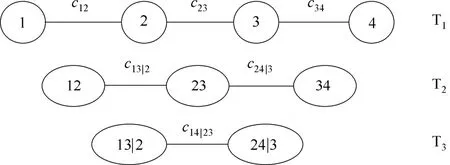
图1 四维D-vine copula结构图Fig.1 Graphical model of four-dimensional D-vine copula

φ表示D-vine密度的所有参数集。

2 D-vine copulas混合模型及其故障检测

vine copula函数在刻画复杂变量之间的高度非线性及尾部特性等方面具有很好的性能，而且在构建多变量相关结构上具有更强的灵活性。将D-vine copula与混合模型相结合，不仅可以更全面地刻画复杂数据间内在的相关性结构，还可以表示出任意复杂的概率密度函数。在此分布模型的基础上，利用高密度区域知识及密度分位数理论构建基于概率的检测指标，实现对过程数据的实时估计。

2.1 D-vine copulas混合模型及参数估计

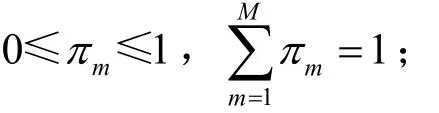
2.1.1 EM 算法 作为处理有限混合模型的通用方法，这里也采用EM算法来估计给定的M元D-vine混合模型的参数 φ，通过极大似然估计的方法进行参数估计。

引入潜在变量zn=(zn1,…,znm,…,znM)，若第 n个观测值xn产生于第m个D-vine元，则znm=1，否则znm=0。假设zn相互独立且服从多项分布，即zn～Mult(M,π=(π1,…,πm))。完备数据(xn,zn)的对数似然函数lc(φ)为[23]

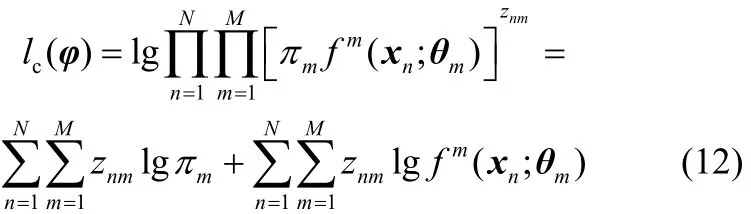
通过EM算法来估计M元D-vine混合模型的参数，具体步骤如下。

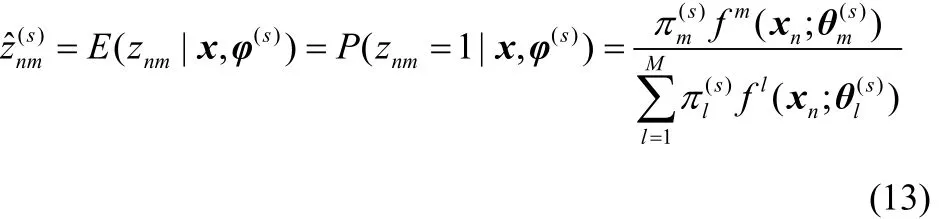
给定参数的初始值φ(0)，然后重复 E-步、M-步迭代计算得到连续的参数估计值φ(s)，s=1,2,…。E-步：在给定的观测数据和当前的参数估计值φ(s)下，计算对数似然函数lc(φ)的条件期望，即计算在当前参数估计值下的观测值xn属于第 m个 D-vine元的后验概率M-步：通过最大化E-步的期望对数似然函数，单独计算每个D-vine元的参数估计值（,…,）和权重参数第m个D-vine元的copula密度参数相当于式（7）通过加权后的参数估计值。R软件中的优化函数optim和constrOptim可以用来最大化式（12）中对应于参数θm的第2项，得到第m个D-vine元的copula参数。

对于性能较好的EM算法，式（11）的似然函数 l(θ)在迭代过程中会不断增大直至收敛，即l(θ(s+1))≥l(θ(s))。因此，迭代终止条件可设为让l(θ(s+1))l(θ(s))的值小于一个预先设定的允许值，如0.00001。有限元混合模型的似然函数存在多个局部最大值[24]。所以，在给定初始值下执行EM算法，在找到的多个局部最大值中选取一个使对数似然函数最大的一组解作为最优解。初始值：本文应用K-means算法获得初步的聚类，K-means算法可以看作是一次硬性的 E-步。进行K-means聚类后，后验概率为

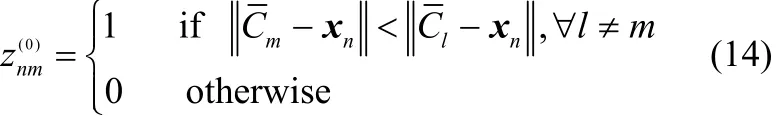
2.1.2 模型的选取 不同结构的二元copula对应着不同类型的相关性结构，尤其是在对尾部相关关系的描述上。如 Clayton能够刻画二维数据的低尾相关性，Gumbel能刻画高尾相关性，而 Gaussian则不具备刻画数据尾部相关性的能力。由于混合模型相关性结构的异构性不可观测，不能获得单个数据点对相关性结构贡献率的先验信息。为简化优化过程，避免优化过程过于繁琐，缩短优化时间，选取4 种典型的二元 copula（Gaussian、Clayton、Gumbel、Frank）作为D-vine copulas混合模型中二元copula的备选类型，并且假设每个 D-vine元的所有二元copula类型相同。

在选定的二元 copula下，混合模型的 D-vine元个数 M 的取值范围为 1～M*。M*一般设置在3～5之间，M*值设置过小不利于变量间复杂相关性结构刻画，M*值设置过大又会导致过拟合现象，也会造成计算量的徒然增加。当M=1时，M 元D-vine copulas混合模型就退化成单个 D-vine copula模型。如果每个D-vine元的二元copula个数为S，则可选的整个混合模型的个数为SM*×。

为了确定混合模型的D-vine元个数M及每个D-vine元中二元copula的类型，这里采用应用最为广泛的模型选取准则：赤池信息准则（Akaike information criterion，AIC）[26]。

从S×M*个混合模型中选择最合适的模型（D-vine元个数M及二元copula类型），找到使模型选取准则AIC取值最小的混合模型。

2.2 故障检测指标的构建

本节的主要目的是在D-vine copulas混合模型的基础上，实现对非线性、非高斯过程的故障检测。这种基于概率的过程监测的关键任务是设计出当前样本数据距离正常数据分布的概率性度量指标。Ren等[16]提出的VCDD过程监测方法实际上就是一种基于数据分布模型的过程监测方法。该监测方法根据高密度区域（HDR）与密度分位数法等理论，构建了广义贝叶斯推断概率（GBIP）指标，通过查询静态密度分位数表的形式，实现对过程的实时监测。

假设过程存在M个D-vine元Dm（m=1,2,…,M），各过程变量间存在复杂的非线性相关性。定义第m个D-vine元Dm的联合PDF为fm(x)，GBIP指标定义如下

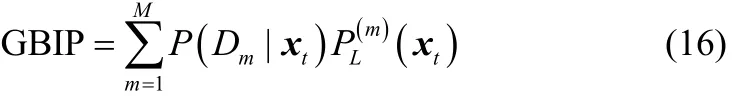
其中，P(Dm|xt)表示当前监控数据 xt属于第 m 个D-vine元Dm的后验概率

下的样本空间且区域内每个点的概率密度要大于等于区域外的点的概率密度。xt关于D-vine元Dm的GLP指标定义为

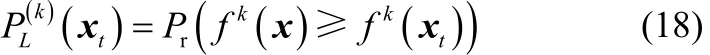
其中fm(x)表示d维随机变量x经过自身PDF映射后的一维随机向量。最后利用离线建立好的静态密度分位数表计算出GLP指标的区间估计值，对于给定的控制限 CL[CL(0, 1)]，判断最终计算出的GBIP指标是否超过了控制限，更多详细过程可参见文献[16]。

2.3 基于D-vine copulas混合模型的故障检测算法流程

基于D-vine copulas混合模型的故障检测过程分为两个阶段：离线建模和在线监控，具体实现步骤总结如下。

离线建模：

（1）获得正常工况下测试数据的正则化秩。（2）从备选二元 copula中为混合模型选择不同的二元copula类型。

（3）在选定的二元 copula下，确定混合模型的D-vine元个数M，M的取值可由1到M*。

（4）根据AIC准则选取，从SM*×个混合模型中选择最终模型。

（5）对于给定的控制限CL，计算训练样本的联合PDF值，构建过程的静态密度分位数表。

在线监测：

（1）利用式（16）结合密度分位数表计算当前监测数据的GBIP指标。

（2）判断GBIP指标是否超限，完成在线的实时过程监控。

3 仿真分析

本章通过数值案例及在TE过程中的应用验证混合D-vine copulas模型的有效性及在处理具有非高斯、非线性的过程数据的故障检测中的良好性能。并分别与有限元高斯混合模型（finite Gaussian mixture models，FGMM）方法[28]和KPCA方法[29]作对比，表明该混合模型取得了较好的检测效果。

3.1 数值实例

通过 R软件的 CDVine软件包中的函数CDVineSim生成测试数据：500组观测数据产生于二元（M2）三维（d3）D-vine密度函数，两个D-vine元具有相同的比例（π1=π2=0.5），各D-vine元的所有二元copula类型为Frank copulas。对测试数据的设定如下：过程在初始的前 50时刻正常运行，然后在接下来的100个时刻，变量X1被赋予一个0.5的偏移项与一个非线性漂移项（故障1），然后过程恢复正常，在最后的150时刻，给以变量X2一个4的偏移（故障2），变量X3始终处于正常状态。图2给出了500组测试数据的时序图（故障数据已用红色标记）。

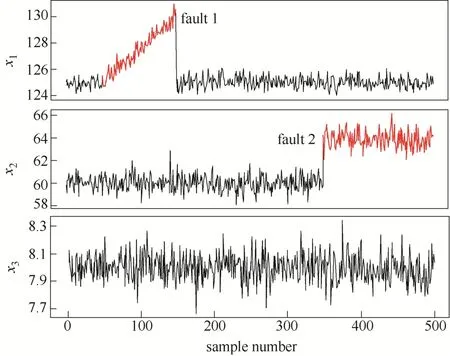
图2 数值例子测试数据时序图Fig.2 Time-series plots of testing data for numerical example

FGMM是建立混合模型的常见方法，通常用来处理非高斯问题。而KPCA方法则是一种非线性方法，其主要思想是将向量空间中的随机向量通过一个非线性函数映射到高维特征空间中，然后在高维空间中进行线性方法研究[29]。为了验证 D-vine copulas混合模型在故障检测中的有效性，用FGMM与KPCA方法作为对比。注意，因为此测试数据来源于一个模态，只涉及利用 HDR建立密度分位数表的过程，FGMM 模型中 BIP指标就相应变成了GLP指标。

图3给出了上述3种方法（FGMM、KPCA、MD-vine）的实时监控图（置信水平0.95）。

为了量化不同方法的检测效果，表1统计了3种方法的监测评价指标：故障检测率（fault detection rates，FDR）和误报率（missing detection rates，MDR）。

检测结果表明，对于故障1（线性漂移），基于MD-vine模型的故障检测方法较FGMM与KPCA方法，故障检测率有明显提高，误报率也相应降低。3种检测方法都能实现对故障2（偏移）的完全检测，但 MD-vine模型的误报率最低，说明了 D-vine copulas混合模型通过准确刻画出数据的分布形式及复杂相关性，找到适用于任意分布的概率性指标，提高了过程的监测效果。

3.2 TE过程

TE过程是由 Eastman化学公司创建的一个用于评价过程控制和监控方法的仿真系统，能较好地模拟实际复杂工业过程系统，作为仿真例子在过程监控领域得到了广泛的应用[30]。TE过程包含41个测试变量和12个操作变量以及21种过程故障，本研究采用了测试变量中的 22个连续过程变量进行分析。在正常运行状态下，采集500组数据作为训练样本，采样间隔为 3 min。测试数据集包含 960个数据样本，在第161个样本点引入故障。

图3 数值例子基于不同方法的实时检测图Fig.3 Real-time monitoring charts based on different methods for numerical example

表1 数值例子监控效果对比分析Table 1 Monitoring performance analysis in comparison study for numerical example

对训练数据进行离线建模，建立静态密度分位数表，然后对测试数据进行在线监测，并分别与FGMM和 KPCA方法作对比。其中，KPCA选取85%的主元，核函数采用高斯核函数图4为3种监测方法对故障20的实时监测图（置信水平 0.98）。显然，MD-vine在开始阶段的检测率明显高于 FGMM 方法，且两种方法的检测效果均显著优于KPCA方法。

图4 3种监控方法对故障20的实时检测图Fig.4 Real-time monitoring charts based on three methods for fault 20

TE过程21个故障中，故障1～7为阶跃变化，故障8～12是随机性故障，故障13是反应动力学中的缓慢漂移，故障14、15和21是与阀黏滞有关的故障，故障16～20未知[31]。表2给出3种方法对各种不同类型的故障都给出了一些具有代表性的检测结果。

由表2可以看出，对于故障1、6、8、13、14，3种检测方法都能取得很好的、相近的检测效果；对于较难检测的故障 4、15，均未取得较好的检测结果，但相对而言，MD-vine方法检测率略好；而对于故障10、16、19、20及21，MD-vine方法与另外两种方法相比有较明显的优势。总体看来，本研究提出的基于MD-vine模型的故障检测方法较两种传统监测方法的监控性能有所提升。对于具有非高斯特征的数据，FGMM中基于马氏距离的概率指标刻画异常数据点的能力降低，而KPCA在数据变换和特征提取的过程中必然造成数据信息的缺失。D-vine copulas混合模型充分利用变量间的相关关系，准确刻画出数据间的分布信息，并且在检测方法上采用更适合非高斯过程的高密度区域法，从而取得比FGMM、KPCA监测方法更佳的检测效果。

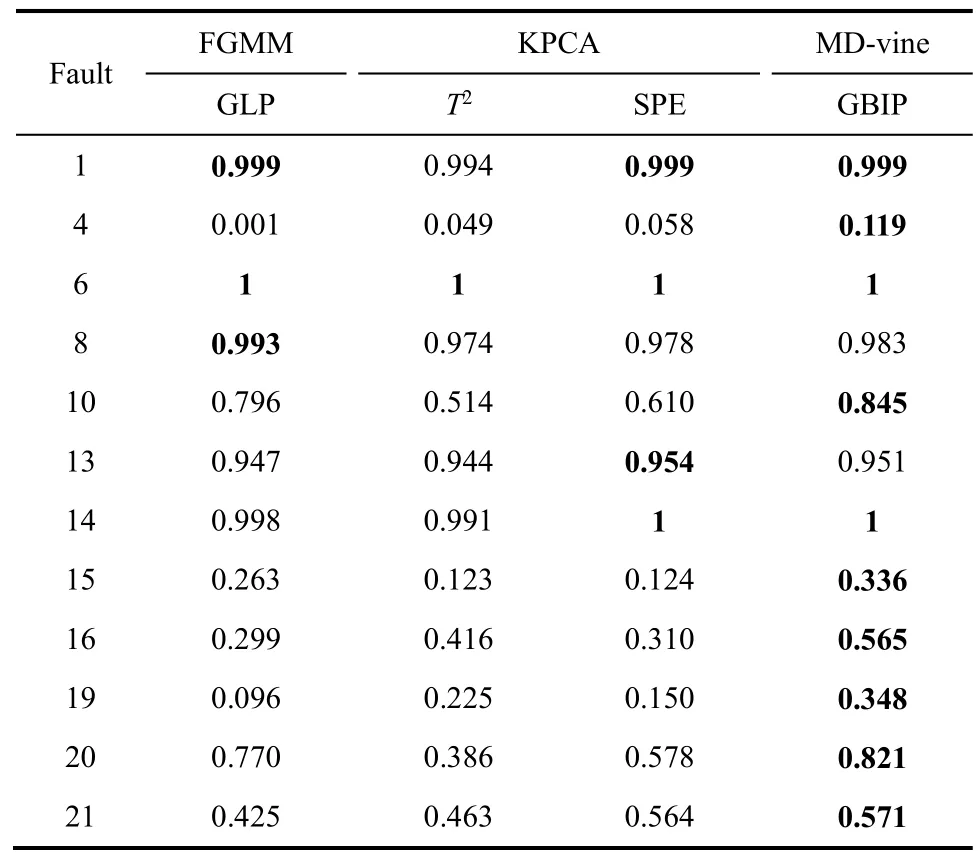
表2 TE过程故障检测率对比分析Table 2 Monitoring performance analysis in comparison study on TE

4 结 论

提出了一种D-vine copulas混合模型，采用EM算法、伪极大似然估计对模型参数进行优化，根据模型选择准则确定最终的估计模型。该混合模型能在不进行降维过程的情况下更深入准确地捕获多元数据间复杂的相关关系，并以得到的分布模型为基础结合高密度区域与密度分位数法等理论实现对存在非线性、非高斯过程故障的实时监测。通过对数值实例和 TE过程进行仿真实验，并与 FGMM 与KPCA方法对比，结果表明此混合模型具有更高的故障检测率和较低的故障误报率。这说明该混合模型方法作为一种新的过程监测方法具有较强的实用性。与降维进行数据特征提取、划分子空间等思想相比，构建数据的分布模型具有更大的优势。此外，该混合模型可以视为半参数模型，兼顾了全参数模型和非参数模型的优点，具有更强的适应性和解释能力，适用范围也更为广泛。在刻画数据间内在的相关性方面，D-vine copulas混合模型具有良好的性能。为简化优化过程，提高参数的优化效率，假设每个D-vine元的所有二元copula类型相同，并且选取了4种典型的二元copula作为D-vine copulas混合模型中二元copula的备选类型。实际上，二元copula族中存在数十种类型的copula。因此，此混合模型在二元copula的选择上仍然有进一步改进的空间。

References

[1] PIOVOSO M J, HOO K. Multivariate statistics for process control [J].IEEE Control Syst. Mag., 2000, 22： 8-9.

[2] 葛志强. 复杂工况过程统计监控方法研究 [D]. 杭州：浙江大学,2009.GE Z Q. Statistical process monitoring methods for complex processes [D]. Hangzhou： Zhejiang University, 2009.

[3] KRAMER M A. Nonlinear principal component analysis using auto associative neural networks [J]. AIChE Journal, 1991, 37 (2)：233-243.

[4] ZHANG Y W. Fault detection and diagnosis of nonlinear processes using improved kernel independent component analysis (KICA) and support vector machine (SVM) [J]. Industrial and Engineering Chemistry Research, 2008, 47 (18)： 6961-6971.

[5] CAI L F, TIAN X M. A new fault detection method for non-Gaussian process based on robust independent component analysis [J]. Process Safety and Environmental Protection, 2014, 92： 645-658.

[6] GE Z Q, SONG Z H. Process monitoring based on independent component analysis-principal component analysis (ICA-PCA) and similarity factors [J]. Industrial and Engineering Chemistry Research,2007, 46： 2054-2063.

[7] DISSMANN J, BRECHMANN E, CZADO C, et al. Selecting and estimating regular vine copula and application to financial returns [J].Computational Statistics and Data Analysis, 2013, 59： 52-69.

[8] SCHOLZEL C, FRIEDERICHS P. Multivariate non-normally distributed random variables in climate research-introduction to the copula approach [J]. Nonlin Processes Geophys, 2008, 15 (5)：761-772.

[9] AHOOYI T M, SOROUSH M, ARBOGAST J E, et al.Maximum-likelihood maximum-entropy constrained probability density function estimation for prediction of rare events [J]. AIChE Journal, 2014, 60： 1013-1026.

[10] JOE H. Families of m-variate distributions with given margins and m(m-1)/2 bivariate dependence parameters [J]. Distributions with Fixed Marginals and Related Topics, 1996, 28： 120-141.

[11] ETIENNE C, MNOIQUE N F. Clayton copula and mixture decomposition [J]. Applied Stochastic Models and Data Analysis,2005, 5： 699-708.

[12] WEIß GREGOR N F, MARCUS S. Mixture pair-copulaconstructions [J]. Journal of Banking & Finance, 2015, 54： 175-191.

[13] ANANDARUP R, SWAPAN K P. Pair-copula based mixture models and their application in clustering [J]. Pattern Recognition, 2014, 47：1689-1697.

[14] NGUYEN C, BHATTI M I, MAGDA K. Gold price and stock markets nexus under mixed-copulas [J]. Economic Modeling, 2016,58： 283-292.

[15] NIKOLOULOPOULOS A K, KARLIS D. Finite normal mixture copulas for multivariate discrete data modeling [J]. Journal of Statistical Planning and Inference, 2009, 139： 3878-3890.

[16] REN X, TIAN Y, LI S J. Vine copula-based dependence description for multivariate multimode process monitoring [J]. Ind. Eng. Chem.Res, 2015, 54 (41)： 10001-10019.

[17] SKLAR A. Fonctions de répartition à n dimensions et leurs marges[J]. Publ. Inst. Statist. Univ. Paris, 1959, 8： 229-231.

[18] REN X, LI S J, LÜ C, et al. Sequential dependence modeling using Bayesian theory and D-vine copula and its application on chemical process risk prediction [J]. Ind. Eng. Chem. Res., 2014, 53 (38)：14788-14801.

[19] BEDFORD T, COOKE R M. Vines—a new graphical model for dependent random variables [J]. Ann. Stat., 2002, 30： 1031-1068.

[20] CHRISTIAN G, ANNE C F. Everything you always wanted to know about copula modeling but were afraid to ask [J]. Journal of Hydrologic Engineering, 2007, 12 (4)： 347-368.

[21] AAS K, CZADO C, FEIGESSI A. Pair-copula construction of multiple dependence [J]. Insurance Math Economic, 2009, 44 (2)：182-198.

[22] OAKES D. A model for association in bivariate survival data [J].Journal of the Royal Statistical Society, Series B, 1982, 44 (3)：414-422.

[23] ANANDARUP R, SWAPAN K P. Pair-copula based mixture models and their application in clustering [J]. Pattern Recognition, 2014, 47：1689-1697.

[24] JEFF WU C F. On the convergence properties of the EM algorithm[J]. The Annals of Statistics, 1983, 11 (1)： 95-103.

[25] CHUNG Y J, LINDSAY B G. Convergence of the EM algorithm for continuous mixing distributions [J]. Statistics & Probability Letters,2015, 12： 190-195.

[26] AKAIKE H. Information Theory and an Extension of the Maximum Likelihood Principle [M]. Budapest： Akadémiai Kiadó, 1973： 267-281.

[27] HYNDMAN R J. Computing and graphing highest density regions[J]. Ann. Stat., 1996, 50 (2)： 120-126.

[28] YU J. Multimode process monitoring with Bayesian inference-based finite Gaussian mixture models [J]. AIChE Journal, 2008, 54 (7)：1811-1829.

[29] LEE J M, YOO C K, SANG W C. Nonlinear process monitoring using kernel principal component analysis [J]. Chemical Engineering Science, 2004, 59 (1)： 223-234.

[30] DOWNS J J, VOGEL E F. A plant-wide industrial process control problem [J]. Comput. Chem. Eng., 1993, 17： 245-255.

[31] JIANG Q C, YAN X F, TONG C D. Double-weighted independent component analysis for non-Gaussian chemical process monitoring[J]. Ind. Eng. Chem. Res., 2013, 52： 14396-14405.

Mixture of D-vine copulas model and its application in fault detection

ZHENG Wenjing, LI Shaojun, JIANG Da
(Key Laboratory of Advanced Control and Optimization for Chemical Processes of Ministry of Education, East China University of Science and Technology, Shanghai 200237, China)

Process monitoring technology is an effective means to guarantee operation safety and product quality of modern industrial processes. Most of traditional process monitoring methods extract data features by dimensionality reduction and require process data obeying Gaussian distribution, linearity and other conditions.Therefore, traditional methods cannot obtain preferable detection results for faults occurred under complex operating conditions. A mixture of D-vine copulas model was proposed for fault detection. First, complex correlation among process variables were directly extracted without dimensionality reduction and a statistical model of process variables was established to accurately describing nonlinear and non-Gaussian processes. Then,model parameters were optimized by expectation maximization (EM) algorithm and maximum pseudo-likelihood estimation. Finally, a generalized Bayesian inference-based probability (GBIP) index was constructed for real-time monitoring by optimized model parameters as well as theories of the highest density region (HDR) and density quantile. Application of the proposed mixture model to a numerical example and the Tennessee Eastman (TE)benchmark process illustrated effectiveness and performance in fault detection.

process monitoring; nonlinear and non-Gaussian; dependence analysis; D-vine copulas

date：2016-11-28.

Prof. LI Shaojun, lishaojun@ecust.edu.cn

supported by the National Natural Science Foundation of China (21406064, 21676086) and the Natural Science Foundation of Shanghai (14ZR1410500).

TP 277

A

0438—1157（2017）07—2851—08

10.11949/j.issn.0438-1157.20161682

2016-11-28收到初稿，2017-03-29收到修改稿。

联系人：李绍军。

郑文静（1992—），女，硕士研究生。

国家自然科学基金项目（21406064, 21676086）；上海市自然科学基金项目（14ZR1410500）。