基于混合界面法的多外挂飞机固有振动特性研究

李智劳 李晓东 刘凡（中国飞机强度研究所，陕西 西安 710065）

基于混合界面法的多外挂飞机固有振动特性研究

李智劳 李晓东 刘凡（中国飞机强度研究所，陕西 西安 710065）

多外挂飞机在固有振动特性测试过程中往往会耗费较长的时间，并且外挂模态可能会与飞机的结构模态耦合在一起，增加了模态识别和分离的难度。本文提出了用混合界面法解决多外挂飞机的固有振动特性问题。采用无外挂飞机的地面共振试验结果和外挂的地面共振试验结果，运用混合界面模态综合理论，对整个全机结构固有振动特性进行分析，获得全机固有振动特性。本文的研究成果可以在飞机挂载方案改变时，快速的对挂载飞机的振动特性进行分析，提高获取带外挂飞机固有振动特性的效率，为研究带外挂飞机的固有振动特性提供了新的方法和途径。

混合界面法；多外挂飞机；固有振动特性；共振试验

由于飞机挂载外挂的组合方案越来越多，全机地面共振试验的周期越来越长，并且由于外挂模态往往会与机翼的低频模态耦合，这使得模态分离的难度增加了不少。目前通过模态综合技术来解决此类问题变得越来越迫切。以往研究模态综合技术主要采取混合建模的方式，即就是划分好的子结构，一部分采用地面共振试验的方式获得结构固有振动特性，另一部分采用有限元计算的方式获得结构的固有振动特性，然后再运用模态综合理论分析整个结构的固有振动特性。然而，由于一部分子结构的固有振动特性是通过有限元计算获得的，对于复杂的结构有限元计算获得的结果往往有较大偏差，最终导致模态综合结果不理想。本文在以往混合建模的基础上，研究了试验-试验模态综合技术。对事先划分好的子结构，都采取地面共振试验的方式来获得结构的模态，然后运用模态综合技术获得整个结构的固有振动特性。

1 混合界面法模态综合理论

模态综合法的基本思想是按复杂结构的特点将其划分为若干子结构；对各子结构进行离散化，通过动力学分析或试验，得到子结构的模态；然后将各子结构的物理坐标—结点位移坐标进行模态坐标变换，并对子结构进行“组集”，获得整个结构的模态坐标；通过子结构的界面连接条件，作第二次坐标变换—独立坐标变换，消去不独立的模态坐标，得到一组用独立的各子结构模态坐标组成的描述整个结构运动的独立广义坐标，从而导出整个系统以独立模态坐标表示的动力学方程。

混合界面模态综合法的基本思想是：把一个结构分成若干个子结构，并把这些子结构分成主子结构和从子结构，但主子结构与主子结构之间，从子结构与从子结构之间互不连接。

如图1所示，以悬臂梁结构为例，图示的梁结构分成两个子结构α、β，子结构α为自由界面，子结构β为固定界面，其物理坐标集{u}分成内部坐标集{ui}和界面坐标集{uj}，即

对主子结构α，用自由界面保留主模态集组成假设模态集，并对其结点物理坐标作模态坐标变换：

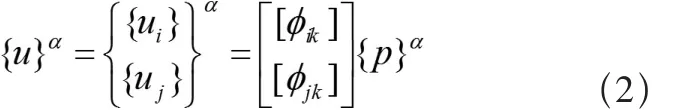
i表示子结构内部节点坐标，k为表示保留主模态及其编号，{ϕik}表示与{ui}对应的i行k列的分支保留主模态矩阵，p表示主模态坐标

对从子结构β，用其固定界面的保留主模态集，与其对界面坐标的约束模态Ψij组成假设模态矩阵，并对结点物理坐标作模态坐标变换：

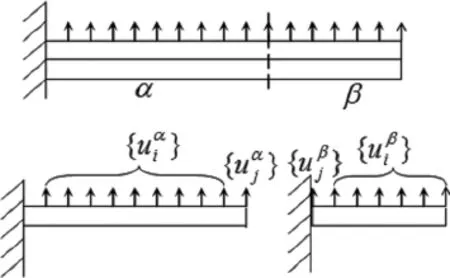
图1 悬臂梁结构及子结构划分

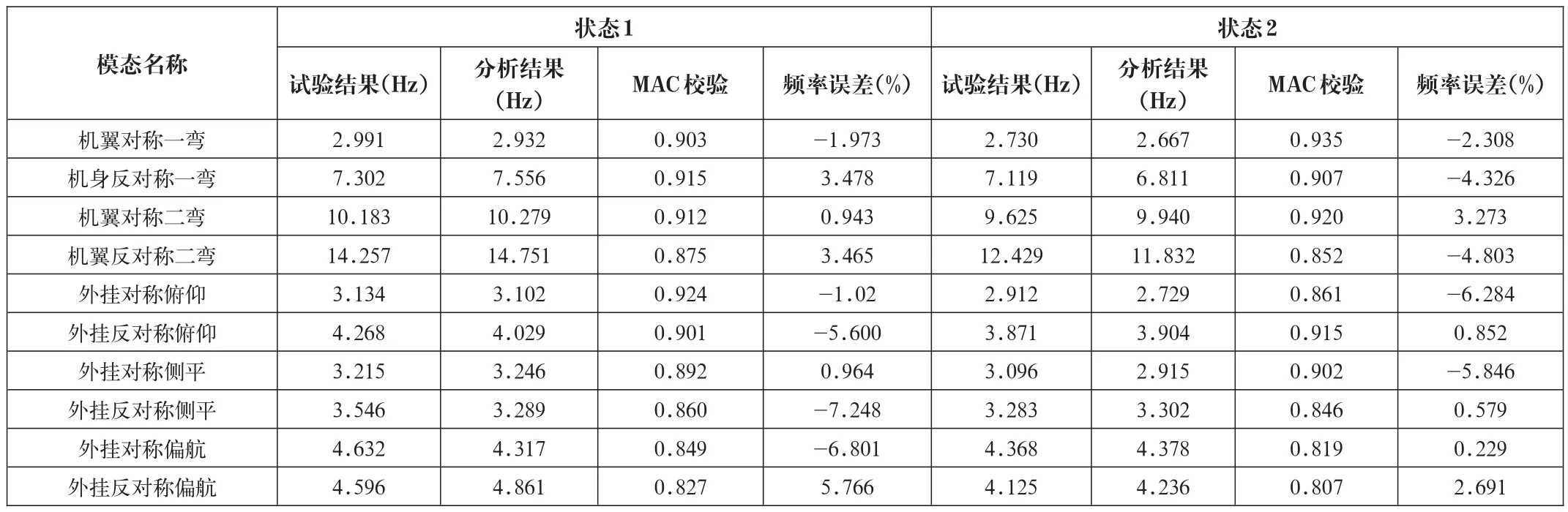
表1 试验及模态综合结果

主从子结构的界面对接条件：

从而可得约束方程：

上式中Φ为子结构主模态，{q}为独立模态坐标。

其中：

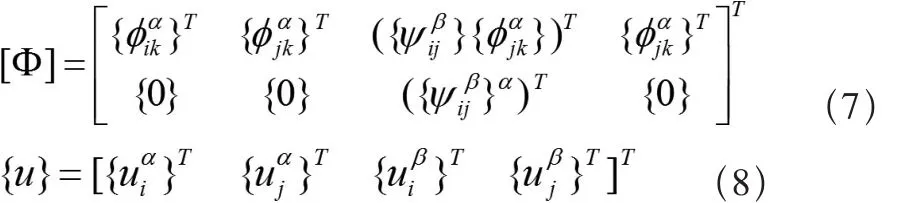
对应于独立模态坐标{q}的质量阵和刚度阵为：

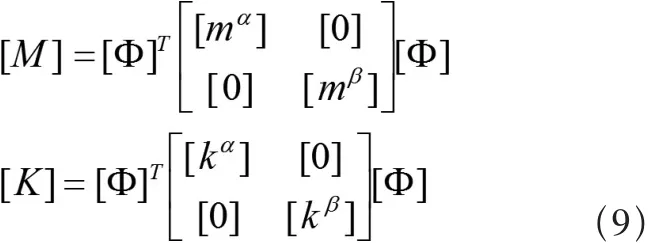
从而得到综合后结构的特征值问题：

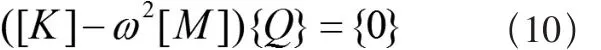
ω为特征值，Q为特征向量。

最后方程度阶数是两个子结构保留主模态数之和，与界面坐标数无关。

2 试验及混合界面法的应用

2.1 子结构划分及试验

本文将全机结构划分为两部分，无外挂飞机及外挂，无外挂飞机在自由-自由状态下进行模态测试，支持方式选择空气弹簧支持。外挂在固支状态下进行模态测试。模态综合过程是自由-自由界面下的无外挂飞机与固定界面下的外挂，即用混合界面法来获得全机结构的固有振动特性。

本次试验的飞机有两种不同的外挂，试验过程中先对不带外挂的飞机在自由-自由状态下进行模态测试，获得不带外挂飞机的固有振动特性。然后再分别对两种不同外挂进行模态测试，获得两种外挂的固有振动特性。对外挂进行测试时，采用固支状态。

子结构α与子结构β的界面界面对接条件为

2.2 模态检验

MAC矩阵表达式为：

式中，i、j—模态阶次；ϕi—第i阶模态振型。

3 试验及模态综合分析

从表1可看出，基于混合界面法的模态综合结果与地面共振试验结果基本一致，这说明，本次运用基于混合界面法的试验-试验模态综合技术获得结构固有振动特性的方法是比较成功的。

4 结语

从本文的结果可看出，基于混合界面法的试验-试验模态综合技术应用于工程实际能够获得比较合理的结果。本文的研究成果对继续研究带外挂飞机的固有振动特性提供了重要参考，并具有一定的工程应用价值。

[1]向树红邱吉宝王大钧.模态分析与动态子结构方法新进展[J].力学进展，2004，34(3)：289-302.

[2]LMS Virtual.Lab Rev 7B On-line help.

[3]姜忻良，王菲.基于势能判据的约束模态综合法截断准则[J].振动与冲击，2011,30（2）：32-38.

[4]汪晓虹安方曹立娟陈怀海.模态综合的直接变换法[J].航空学报，2009，30（1）：92-98.

[5]冯海星刘海立张松波高云凯.模态综合法在车身结构动力学计算中的应用[J].汽车工程，2012，34（09）：811-815.

[6]宋攀董兴建孟光.实验模态综合法若干问题的研究[J].振动与冲击，2011，30（09）：174-177.