三种块缺失数据处理方法的比较*
南京医科大学公共卫生学院生物统计学系(211166)
林丽娟 董学思 赵 杨 魏永越 戴俊程 陈 峰△
三种块缺失数据处理方法的比较*
南京医科大学公共卫生学院生物统计学系(211166)
林丽娟 董学思 赵 杨 魏永越 戴俊程 陈 峰△
跨平台组学数据(cross-platform-omics data)研究中,一组样本往往只在某些平台(例如蛋白组学、代谢组学等)上进行了测序分析,而另外一些样本在其他平台(例如,基因组学、蛋白组学等)上进行了测序,欲将不同平台的数据进行整合分析,则块缺失(block missing)是不可避免的。由于块缺失的缺失比例比较高,如果将含有缺失的观测全部剔除,仅对完整数据进行分析,则会损失大量信息,甚至无信息可用。传统上,常用的缺失数据处理方法是基于填补(imputation)的方法,包括单一填补法(如均值填补、回归填补、hot deck填补等)和多重填补法[1-2]。然而这些方法适用于缺失比例不太高的情况,如果采用传统填补方法对块缺失数据进行填补,可能会导致估计偏差较大,或耗时太多,从而大大降低了统计分析的效率。如何处理这类缺失数据,将是跨平台组学大数据研究中急需解决的一个问题。
不同于目前常用的基于填补的缺失处理方法,不填补的方法不对缺失数据进行填补,而是利用不完整数据集中所有变量可利用的全部信息 ,来构建变量之间的方差-协方差结构或者极大似然函数,并据此来估计回归模型的参数,则可以达到充分利用已有数据信息的目的,即不完整数据的全信息估计。基于此思路,本研究采用数据模拟技术,比较三种不填补的方法:列表删除法(listwise deletion,LD)、配对删除法(pairwise deletion,PD)以及全信息极大似然法(full information maximum likelihood,FIML)处理块数据的优劣。
缺失值处理方法
1.列表删除法
将数据集中含有缺失的记录全部删除后得到“完整数据集”,对该“完整数据集”采用常规的统计方法进行分析,因此此方法也称为完整观测分析(complete case analysis)。该方法适用于任何一种分析,是很多统计分析软件默认的缺失值处理方法[3]。
2.配对删除法
在计算某一统计量时,仅将两两变量间的缺失记录删除,而不考虑其他变量的缺失情况,如:在计算x1和x2的相关系数时,只将x1或x2中缺失的记录删除,而忽略其他变量的缺失情况[3]。与列表删除法相比,该方法利用更多的样本信息,在一定程度上避免了列表删除法所造成的样本信息大量损失,统计检验功效降低等问题。
3.全信息极大似然
在构造极大似然函数时,只利用每个观测中没有缺失的完整变量,而不考虑该观测中缺失的变量。通过计算,得到N个观测的N个极大似然函数,然后将这N个极大似然函数相加,得到基于全部观测的极大似然函数。其表达式如下:
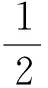
其中xi表示第i个观测中完整变量的数值,μi是第i个观测中这些完整变量的均值向量,Σi是其方差协方差矩阵,Ki是与第i个观测中完整数据个数相关的常数[4]。
模拟研究
应用SAS 9.2进行编程,模拟完整数据集,样本量为n=1000,包括1个因变量和p个服从多元正态分布的自变量x1,x2,…,xp。对该数据集构建一个多元线性回归模型:
y=β0+β1x1+β2x2+……+βpxp+ε
估计模型的参数以及标准误。对完整数据集构造不同缺失率的数据集,分别采用列表删除法、配对删除法和全信息极大似然法对每种缺失率的数据集进行处理,得到模型参数的估计值及其标准误,对每种缺失率的数据均模拟1000次,得到各模型参数的估计值及标准误的平均值,并与所设置的理论值进行比较。
1.模拟研究一:一个块缺失
考虑5个自变量与1个因变量的回归,所构建的多元线性回归模型如下:
y=3+2x1+4x2+6x3+8x4+10x5+ε1ε1~N(0,σ2)
其中 ,X1=(x1,x2,……,x5),X1服从多元正态分布,即X1~N(μ1,∑1)。其中μ1和∑1分别表示均值向量与方差-协方差矩阵,其表达形式如下:
假设数据集中仅(变量x1,x2,x3)呈块缺失,即同时缺失或同时不缺失,缺失比例分别考虑10%,30%,50%,70%四种情况,而其他变量均是完整的。
2.模拟研究二:两个块缺失
考虑8个自变量和1个因变量的回归,所构建的多元线性回归模型如下:
y=3+2x1+4x2+6x3+8x4+10x5+9x6+7x7+5x8+ε2ε2~N(0,σ2)
记X2=(x1,x2,……,x8),X2服从多元正态分布,即X2~N(μ2,∑2)),其中μ2和∑2分别表示均值向量与方差-协方差矩阵,其表达形式如下:
假设数据集中(变量x1,x2,x3)呈块缺失,(变量x6,x7,x8)也呈块缺失,考虑两个块缺失比例同时为30%、35%、40%、45%四种情况,而其余变量均是完整的。
3.评价标准
(1)标准偏差:当标准偏差大于0.4时,偏差会对功效、置信区间覆盖率以及误差率产生影响[5]。因此,若某种方法的标准偏差小于0.4,认为此方法的估计偏差尚可接受。标准偏差的计算公式如下:


(2)参数的标准误:用参数估计的标准误的均值来衡量各方法的估计精度[5]。
结 果
1.模拟研究一:一个块缺失
模拟1000次,由于结果相似,这里仅仅列出缺失率为30%,50%时各缺失值处理方法的结果,见表1、表2。从结果可以看出,无论缺失率为多少,LD、PD以及FIML的标准偏差均小于0.4(截距项除外),因此可认为这三种缺失值处理方法的估计偏差尚可接受。而从估计精度上看,FIML最优,PD次之,LD最差。
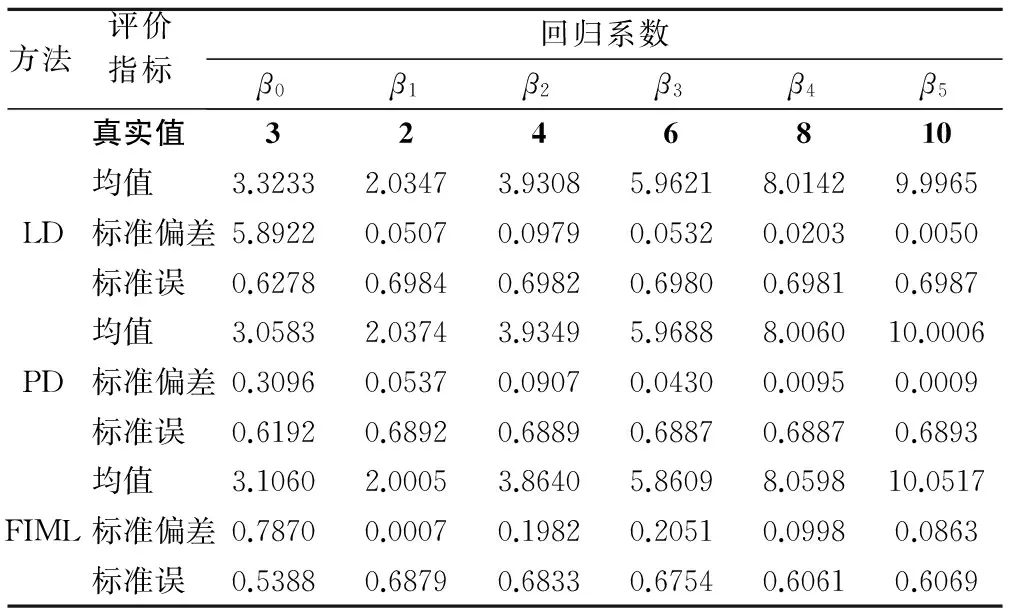
表1 缺失率为30%时各缺失值处理方法比较(模拟研究一)
图1为不同缺失率下,各方法对完整变量x4的参数估计标准误的变化情况。从图中可以看出,在缺失率为10%时,三种方法的标准误相差不大,但随着缺失率的增加,LD和PD的标准误均有明显的增大,总体上PD优于LD,而FIML的标准误比较稳定,增幅不大,且明显优于LD和PD。

表2 缺失率为50%时各缺失值处理方法比较(模拟研究一)
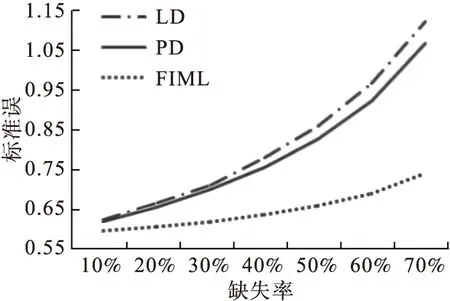
图1 回归系数β4在不同缺失率下的估计精度(模拟研究一)
2.模拟研究二:两个块缺失
模拟1000次,由于结果相似,这里仅列出缺失率为60%,80%时各缺失率处理方法的结果,见表3、表4。从结果可以看出,三种缺失值处理方法的标准偏差均小于0.4,说明三种方法的估计偏差尚可接受。对于含有缺失的变量(不完整变量),PD的标准误最小,FIML次之,LD最大。而对于完整变量x4,x5而言,FIML的标准误最小,PD次之,LD的最大。
图2为不同缺失率下,各方法对完整变量x4的参数估计标准误的变化情况。从图中可以看出,随着缺失率的上升,LD的估计标准误明显增加,而FIML和PD的标准误增幅不大,FIML的标准误略小于PD。
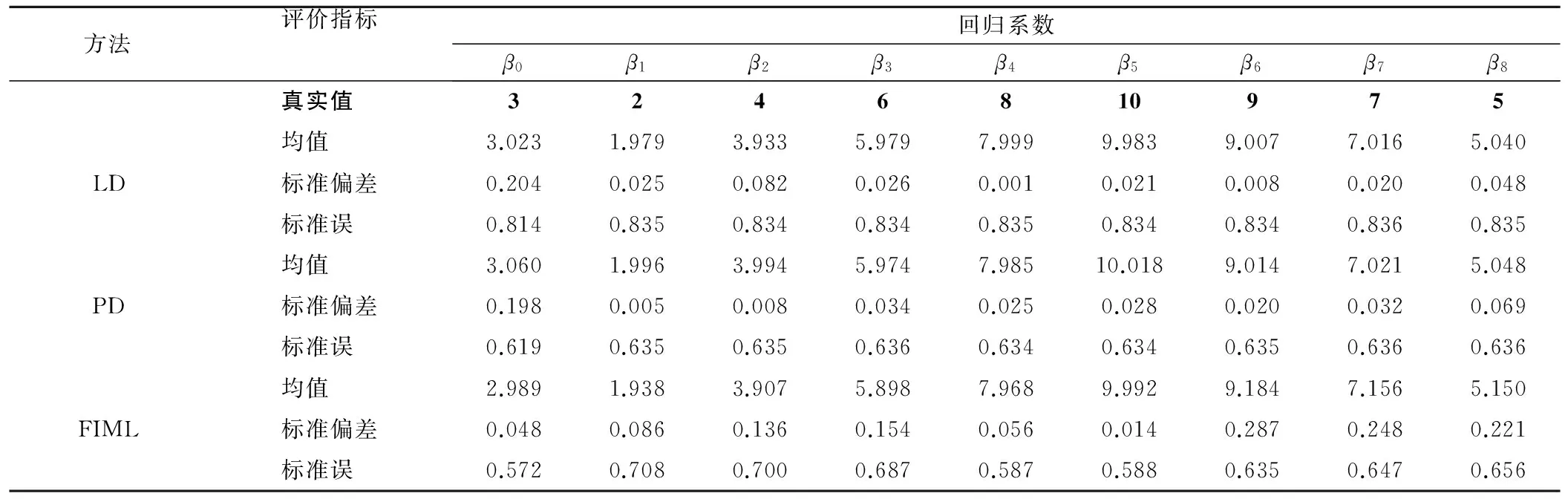
表3 数据集缺失比例为60%时各缺失值处理方法比较(模拟研究二)

表4 数据集缺失比例为80%时各缺失值处理方法比较(模拟研究二)
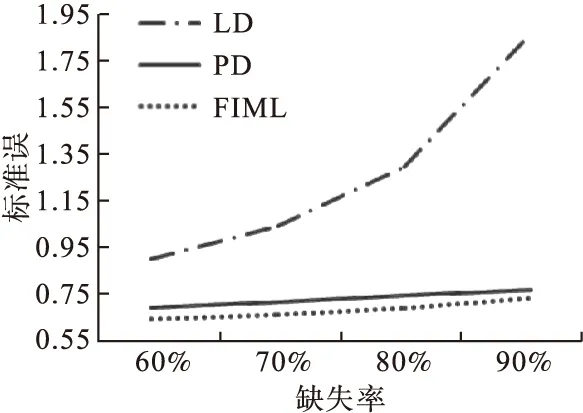
图2 回归系数β4在不同缺失率下的估计精度(模拟研究二)
讨 论
本研究结果显示,当缺失比例比较小(如<10%)时,列表删除法、配对删除法和全信息极大似然法的估计偏差和估计精度都差不多。随着缺失比例的增大,列表删除法和配对删除法的估计标准误均有明显的上升趋势,而全信息极大似然法的估计标准误增幅不大,且明显小于前面二者。当缺失比例很大时(如>70%),全信息极大似然法对完整变量的估计精度略优于配对删除法,而对不完整变量的估计却远差于配对删除法。
列表删除法因为简单,容易实施而被广泛应用,在很多统计分析软件中是默认的缺失数据处理方法[6-7]。但在跨平台组学数据整合分析中,数据存在很多的块缺失,若采用列表删除法直接将缺失数据删除,则会损失大量数据信息,导致统计分析效率低下。从上述的模拟研究的结果可以看出,当缺失率比较小时(如10%),列表删除法的效果尚可,随着缺失率的上升,列表删除法的估计精度不佳,与Baraldi等的结论一致[7-9]。
配对删除法和全信息极大似然法都是基于不填补的思想[10],充分利用已观测到的数据信息,避免了由于列表删除法所造成的数据信息大量损失等问题,因此这两种方法在估计精度上均优于列表删除法。目前常用的缺失数据处理方法是多重填补法[11-13]。有研究表明[14-15],多重填补的估计效果与全信息极大似然法相近,但全信息极大似然法的计算效率更高。而且,对于一个给定的数据集,全信息极大似然法每次的估计结果一致,而由于随机性,多重填补会得出不一样的结果。本研究结果表明,当数据中仅存在一个块缺失时,全信息极大似然法对所有变量的估计标准误均小于配对删除法,而当数据存在两个块缺失时,仅对于完整变量而言,全信息极大似然法的标准误小于配对删除法,对于含有缺失的不完整变量,刚好相反。Yung[10]等人的研究表明,当数据集中的缺失比例超过85%时,全信息极大似然算法会不收敛。当数据存在两个块缺失时,即数据集的缺失比例很大,全信息极大似然法会因算法不收敛而效果不佳,不如配对删除法。当块缺失数据的缺失比例不是很大时(如<70%),推荐采用全信息极大似然法,因为在估计偏差均可接受的情况下,其估计精度最优。当缺失比例超过70%时 ,三种方法的标准误均比较大,推荐采用配对删除法,因为其估计精度相对较优。
块缺失是跨组学平台研究中经常遇到的问题,目前尚无关于这方面的研究。不同于目前广泛应用的基于填补的方法,本研究采用不填补的方法对块缺失进行处理 。尽管所研究的变量不多,但是对于方法评价来说,已经能够说明各自的优劣。这为进一步充分利用不同组学平台的信息以及环境暴露信息进行疾病风险预测、预后预测等提供了方法选择的理论依据。
[1]Abraham WT,Russell DW.Missing data:a review of current methods and applications in epidemiological research.Current Opinion in Psychiatry,2004,17(4):315-321.
[2]帅平,李晓松,周晓华,等.缺失数据统计处理方法的研究进展.中国卫生统计,2013(1):135-139.
[3]Enders CK.Applied missing data analysis.Guilford Press,2010,39-42.
[4]Enders CK.The performance of the full information maximum likelihood estimator in multiple regression models with missing data.Educational and Psychological Measurement,2001,61(5):713-740.
[5]Burton A,Altman DG,Royston P,et al.The design of simulation studies in medical statistics.Statistics in medicine,2006,25(24):4279-4292.
[6]Graham J.Missing data analysis:Making it work in the real world.Annual review of psychology,2009,60:549-576.
[7]Baraldi A,Enders CK.An Introduction to Modern Missing Data Analyses.Journal of School Psychology,2010,48(1):5-37.
[8]Myers TA.Goodbye,listwise deletion:Presenting hot deck imputation as an easy and effective tool for handling missing data.Communication Methods and Measures,2011,5(4):297-310.
[9]Kang H.The prevention and handling of the missing data.Korean journal of anesthesiology,2013,64(5):402-406.
[10]Yung YF,Zhang W.Making use of incomplete observations in the analysis of structural equation models:The CALIS procedure's full information maximum likelihood method in SAS/STAT®9.3.SAS Global Forum,2011:1-20.
[11]Royston P.Multiple imputation of missing values:further update of ice,with an emphasis on categorical variable.Stata Journal,2009,9(3):466-477.
[12]Lee K J,Carlin JB.Multiple Imputation for Missing Data:Fully Conditional Specification Versus Multivariate Normal Imputation.American Journal of Epidemiology,2010,171(5):624-632.
[13]Moniek CM,Merel VD,Kitty JJ,et al.Multiple imputation:dealing with missing data.Nephrology Dialysis Transplantation,2013,28(10):2415-2420.
[14]Allison PD.Handling missing data by maximum likelihood.SAS global forum,2012,23:1-21.
[15]Newman DA.Missing data five practical guidelines.Organizational Research Methods,2014,17(4):372-411.
(责任编辑:郭海强)
国家自然科学基金(81530088,81473070,81373102,81402764)
△通信作者:陈峰,E-mail:fengchen@njmu.edu.cn

