基于区间模糊数EA-GRD-TOPSIS法的医疗满意度综合评价模型研究*
张利平 唐云锋 吴学谦 李望晨△
·应用研究·
基于区间模糊数EA-GRD-TOPSIS法的医疗满意度综合评价模型研究*
张利平1,2,3唐云锋1,2,3吴学谦1,2,3李望晨1,2,3△
目的 以基于区间直觉模糊数形式的多指标综合评价方案设计为视角,探索以EA(误差分析法)、GRD(灰色关联度)、TOPSIS(逼近理想解)法构建模型并验证其应用可行性。方法 将属性值以区间模糊数表示,由均值矩阵、偏差矩阵计算灰色关联度区间数、可能度、排序数,以相对贴近度来排序或择优。以医疗满意度综合评价为算例演示实施过程。结果 满意度偏好认识适用于区间模糊数表示;各部分均有相关理论支持,并可在excel软件中逐步实现。结论 区间模糊数与EA、GRD和TOPSIS法结合,适于满意度等主观属性综合评价建模应用,也适用于卫生综合评价问题。
区间模糊数 灰色关联度 TOPSIS 医疗满意度 评价
多属性决策或评价问题就是综合利用属性、属性值和权重,经信息集结后将有限个对象或方案相对排序或择优。主观偏好认识属性值常用模糊数表示,模糊综合评判方法常见[1-3],如医疗满意度评价、诊疗方案决策等问题,属性值以模糊隶属度表示,将隶属度矩阵与权重向量按逻辑算法生成综合隶属度,由此进行对象或方案比较,计算过程较为简单。
鉴于主观偏好不确定性,属性测度以固定数值表示不如以区间数表示更显合理。传统综合评价方法难以有效利用区间模糊数信息,有必要探索建模新方法。随着模糊数学、运筹学、系统科学和决策科学理论的完善,基于属性值区间模糊数的信息集结算法受到关注。本研究将以区间模糊数建模算法设计为立足点,以理论基础为支撑,引入区间模糊数、随机误差分析、灰色关联度和TOPSIS法,以患者满意度综合评价问题为载体,阐述建模流程、演示算例操作,旨在为卫生综合评价领域类似问题研究提供方法借鉴。
理论流程
基本思想是将待评对象关于每个属性值表示为区间模糊数,将区间模糊数无量纲化预处理,由区间左、右端点值得到均值矩阵、偏差矩阵,由均值矩阵构造正、负理想解,计算每个对象与正、负理想解的灰色关联系数、加权灰色关联度。引入随机误差分析知识,得到每个对象与正、负理想解灰色关联度区间。两两比较计算区间数的可能度,计算每个对象关于正、负理想解排序数。由逼近理想解及相对贴近度,将对象或方案进行综合排序或择优。
1.区间模糊数知识
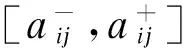
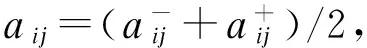
(1)

(2)
2.区间模糊数灰色关联度

(3)
(4)
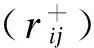
从而形成向量
(5)

(6)

其中区间数
(7)
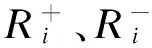
3.区间模糊数可能度、排序数
令la=a+-a-,lb=b+-b-,定义区间数[a-,a+]≥[b-,b+]的可能度[5]:
p([a-,a+]≥[b-,b+])=max(1-max((a+-b-)/((a+-a-)+(b+-b-)),0),0)
(8)
另外还有p([a-,a+]≥[b-,b+])=(max(a+-b-,0)-max(a--b+,0))/((a+-a-)+(b+-b-))等公式。
由公式(8)计算两类区间数的可能度:
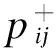
(9)

(10)
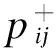
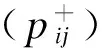
(11)
(12)
数值Ci越大则对象Ai越优,据此可对{A1,A2,…,Am}相对排序或择优。
算例实现
1.资料
以患者满意度评价为例,针对区间模糊数EA-GRD-TOPSIS法建模方案流程验证实现可行性,经流程设计和算例演示为医院管理工作者借鉴。
从医院门诊、住院维度细分满意度属性,门诊维度(0.45):{候诊u1(0.34)、检查u2(0.37)、取药u3(0.29)};住院维度(0.55):{手术u3(0.35)、护理u4(0.34)、指导u5(0.31)},括号内为权重。
以三所教学医院{A1,A2,A3}为例,设计调查问卷并制定满意度评语{“不满意”、“不算理想”、“还算可以”、“满意”},满意隶属度=((“满意”数×2+“还算可以”数×1)/3)/有效问卷数,经剔除无效问卷后得到有效问卷数。不同时期患者满意度调查结果有差异,在医院行政部门协调下,间隔多个时间段分别实施,限于篇幅及重点,问卷设计和调查过程不作祥述。
以医院A1关于属性u11为例,区间模糊数值[0.63,0.71],说明满意度介于63%~71%。所有属性均为满意隶属度,介于0~1,不必无量纲化预处理。
2.区间模糊数灰色关联度
由(1)、(2)计算区间模糊数的均值矩阵A=(aij)3×6、偏差矩阵E=(eij)3×6:
由A=(aij)m×n确定正理想解A+=(0.740,0.720,0.855,0.700,0.735,0.855);负理想解A-=(0.670,0.665,0.815,0.640,0.710,0.820)。
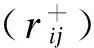
两个维度权重归一化处理为(0.1530,0.1665,0.1305,0.1925,0.1870,0.1705)。
由(5)计算{A1,A2,A3}关于A+、A-的加权灰色关联度:
η+=(0.482,0.598,0.936),
η-=(0.898,0.749,0.458)。
3.区间模糊数误差分析
由(6)计算Δη+=(0.166,0.180,0.329),Δη-=(0.298,0.255,0.161)。
由(7)计算{A1,A2,A3}关于A+、A-的灰色区间数向量:
R+=([0.316,0.648],[0.418,0.778],[0.607,1.265]);
R-=([0.600,1.196],[0.494,1.004],[0.297,0.619])。
由(9)、(10)计算可能度矩阵
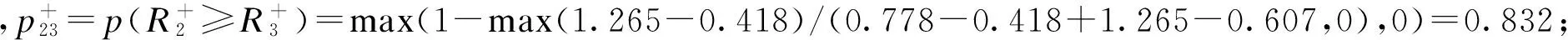
4.相对贴近度及排序
由(11)计算{A1,A2,A3}的排序数向量V+=(0.916,1.224,1.860);V-=(1.743,1.543,0.781)。
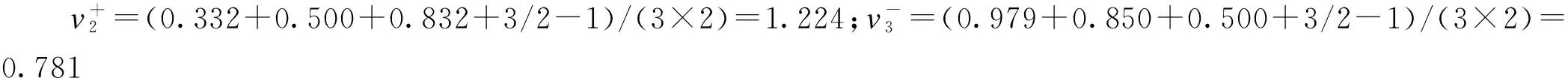
由(12)计算{A1,A2,A3}相对贴近度Ci:(0.344,0.442,0.704)。
据此比较{A1,A2,A3}综合满意度,经相对排序为A3≻A2≻A1,说明A3最优。
实际上,也可分别在门诊、住院维度下建立满意度综合评价模型。对于属性体系多层且复杂、对象或方案数很多的综合评价问题,这套方法仍适用。
讨 论
1.模糊属性评价值以区间模糊数表示,更有利于描述评价者属性偏好认识规律。区间模糊数经均值灰色关联度计算后,以随机误差分析理论,融入区间模糊数偏差信息并得到关联度区间。可能度用来两两比较灰色关联度区间值,在合理利用信息基础上计算排序数。最后用逼近理想点法给出所有对象相对排序。该法融合并有效利用了所有对象关于属性偏好认识信息,对于多属性决策或评价问题应用有优越性。决策科学及系统工程方法有必要引入医疗服务、卫生管理领域,继续探索应用问题的技术方案设计。
2.本文以医疗服务患者满意度综合评价问题为算例,在门诊和住院维度下构建满意度指标或属性体系,每个属性经调查后满意度值表示为区间模糊数,由每个待评医院关于所有满意度属性制定区间模糊数决策矩阵。引入灰色关联度(GRD)、随机误差分析(EA)和逼近理想解(TOPSIS)等方法构建模型,给出各医院满意度综合评价结果。在理论流程阐述基础上,计算步骤均在excel单元格中编排实现,应用工作者可根据算法程序或工具,类似地套用于其他问题研究。该法对于属性模糊数为区间值形式资料有适用性,突破了卫生综合评价问题传统思路,对医疗卫生领域多属性决策或多指标评价有技术扩展意义。
[1]张立威,黄婉霞,王家骥.应用模糊综合评判法评价社区卫生服务患者满意度.中国卫生事业管理,2013,(12):890-892.
[2]刘卉,邹波,卢光耀,等.应用模糊综合评价法评估医务人员工作满意度.中国卫生统计,2012,29(4):561-562.
[3]樊宏,邬银燕,王乾元.基于模糊集理论的社区卫生服务利用者满意度分析.中国卫生统计,2014,31(5):823-826.
[4]高岩.基于模糊决策矩阵的多属性决策方法研究.南京航空航天大学博士学位论文,2010年.
[5]张市芳.几种模糊多属性决策方法及其应用.西安电子科技大学博士学位论文,2012年.
[6]徐泽水.模糊互补判断矩阵排序的一种算法.系统工程学报,2001,16(4):311-314.
(责任编辑:郭海强)
*资助项目:教育部人文社科基金课题(15YJCZH087);山东省自然科学基金(ZR2015HL101);山东省高校人文社科课题(J14W21);中华医学会医学教育项目(2016A-RW007)
1.潍坊医学院公共卫生与管理学院(261053)
2.社会领域健康风险协同创新中心
3.“健康山东”重大社会风险预测与治理协同创新中心
△通信作者:李望晨,E-mail:lwch.ppt@163.com.

