基于小波包分解和改进差分算法的神经网络短期风速预测方法
黄勇东,陈冬沣,肖建华,林艺城,董朕
(1.广东电网有限责任公司揭阳供电局,广东揭阳522000;2.广东工业大学自动化学院,广州510006)
基于小波包分解和改进差分算法的神经网络短期风速预测方法
黄勇东1,陈冬沣1,肖建华1,林艺城2,董朕2
(1.广东电网有限责任公司揭阳供电局,广东揭阳522000;2.广东工业大学自动化学院,广州510006)
风速预测在风电场的智能管理和安全并网中起着至关重要的作用,针对风速预测固有的波动性、间歇性和非线性等特点,以及常规BP神经网络和差分算法神经网络均存在容易陷入局部最优导致收敛过早、泛化能力不足等缺陷,提出一种综合WPD和IDE算法的短期风速预测神经网络方法。该方法首先利用WPD将风速的时间序列分解成多种不同频率的子序列,然后采用IDE算法优化后的神经网络对小波包分解后的每个不同频率的子序列进行单步预测,最后将预测后的各个子序列进行叠加,得出最终预测结果。为验证所提方法的有效性,将其分别与采用混合小波分解的BP神经网络风速预测方法和混合小波分解的差分算法风速预测神经网络方法进行对比,对某地区的实际风速数据进行实验仿真,结果表明,所提方法的预测精度明显优于其他算法。
差分算法;小波包分解;风速预测;神经网络
0 引言
风能作为一种极具前景的清洁、可再生能源,在低碳能源领域发挥着越来越重要的作用[1,2]。由于风速固有的随机性和间歇性给电网电能质量和供电可靠性带来严重冲击,给大规模风电并网出了很大的难题。针对这一问题,通常采取增加常规发电机组的旋转备用容量,但这急剧增加了整个电力系统的运行费用[3]。因此,对风速进行较准确的预测,不仅能够使调度部门在参与发电竞价时及时作出正确的调度决策,有效降低整个系统的运行成本,同时还可有效减轻风电在大规模并网时对电网造成的影响。
在过去的几十年里,已经出现很多种短期风速预测的方法,有基于数值天气预报数据进行风速预测的物理模型预测方法,也有利用数据之间相关性进行风速预测的历史数据风速预测方法,这2种方法各有优缺点[4]。在我国,由于缺乏系统的数值气象信息,因此,通常采用基于历史数据的方法进行预测,其常用方法包括持续法[5]、随机时间序列法、卡尔曼滤波法[6]、支持向量机法[7]、神经网络法[7]以及小波分析[8]等。近年来,由于神经网络在信息处理规模以及学习能力等方面的优势,受到广大研究人员的认可。但该方法存在过拟合、泛化能力不足、最优网络结构难以确定等缺陷。神经网络的预测精度主要取决于各神经元间的权值和阈值,目前普遍的权值优化方法有模拟退火法[9]、粒子群算法[9]、蚁群算法[10]、遗传算法[11]以及多种组合算法[12]等,虽然已有实验证明应用这些方法来优化网络的权值、阈值能够取得一定的效果,但各算法均存在容易陷入局部最优的问题。截至目前,高维的神经网络权值和阈值优化仍然是启发式算法在解决大规模多峰优化问题上的一大挑战。
针对以上风速预测方法的特点和不足,提出一种基于WPD-IDE-NN(混合小波包分解和改进差分算法的神经网络)短期风速预测方法,并对某实际风电场的风速进行提前24 h预测,取得了良好的预测效果。
1 小波包分解
WD(小波分解)是一种能将原始信号分解成多个子序列的分解技术,并且当多次分解时,每次仅进行低频部分再分解,高频分量并没有再次分解,这种仅针对低频分量细化分解的模式对不同的分解目的而言不一定能达到最优的分解效果[13]。WPD(小波包分解)则可以有效解决上述问题,WPD对原始信号在同一级尺度上同时将低频和高频信号分量分解成多个不同频率子序列的数学方法,这一过程能够形成一个完整的二叉树结构(如图1所示),分解得到2i个子序列,i为分解层数,即尺度数。

图1 三层WPD结构
2 改进差分优化算法
2.1 标准差分进化算法
标准DE(差分进化)算法的基本思想是:利用种群中个体之间的差分向量对个体进行扰动以实现个体突变,通过目标个体与变异个体的交叉突变策略产生新个体,种群通过优胜劣汰得到进化。DE算法通过多次迭代搜索最终获得全局最优解,该算法不仅具备结构简单、控制参数少、易于实现、鲁棒性较强等优点,而且其固有的并行性有助于算法求解大规模系统模型。DE算法主要包含初始化种群、突变操作、交叉操作和选择操作。
2.1.1 初始化种群
设NP为种群大小,D为个体的维数,k为进化代数,Xk为第k代种群。首先在问题的决策空间内随机产生第0代种群其中表征第0代种群中的第i个粒子。
个体的每一维可以由公式(1)生成:

式中:Lj为第j维变量的下限;Uj为第j维变量的上限;rand()为0到1的随机数。
2.1.2 突变操作
在父代种群中,利用公式(2)对第k代种群中的每一个个体xi执行变异操作,获得与其对应的突变个体:

式中:r1,r2,r3∈{1,2,…,NP}且互不相同,同时与i不同;为父代基向量;()称为父代差分向量;MF为0~2的随机数,并称为缩放比例因子。
2.1.3 交叉操作

式中:rand(j)为0~1的均匀分布随机数;probability_DE为范围在0~1的交叉概率。
2.1.4 选择操作
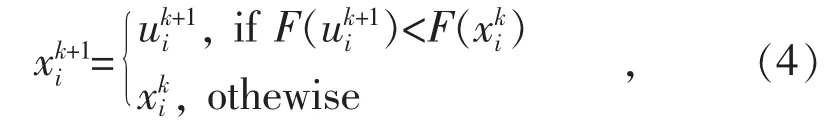
式中:F为目标函数。
标准DE算法的性能主要取决于其全局搜索和局部探测能力,一定意义上而言,这取决于该算法交叉概率的设置。相比于其他的启发式算法,DE算法调节参数少,可操作性强,群体搜索,具有记忆个体最优和全局最优功能等优点。然而,与遗传算法、蚁群算法、粒子群算法等绝大多数启发式算法相似,DE算法由于其固有利用差分向量进行突变产生新个体的搜索方式导致在迭代达到一定次数时,种群多样性急剧下降,形成“聚集”现象并产生过早收敛的问题[14]。
2.2 改进差分算法
2.2.1 种群方差计算
针对上述问题,提出以下改进:由公式(2)和(5)可知,DE算法是利用个体之间的差异来突变产生新的个体,因此当迭代达到一定次数时,由于“聚集”现象,整个种群中的每一个体差异几乎为0,即公式(5)计算出种群的方差E趋于0:
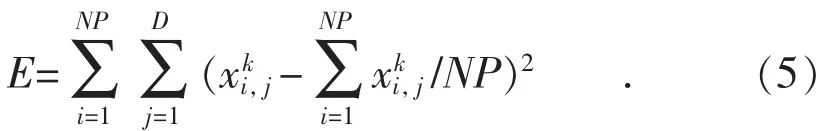
此时,由于个体之间无差异导致无法产生新的突变个体,造成整个种群陷入局部最优值,因此在执行DE算法之前需进行种群方差计算,当种群方差E小于某一极小值MV(通常取10-20)时则不执行差分进化算子,转而进入引进的纵向交叉操作。
2.2.2 纵向交叉操作
纵向交叉操作是对种群中所有维进行随机两两不重复配对后,以概率形式选择配对维执行纵向交叉的一种算数交叉操作。针对可能存在的不同维因取值范围不同无法直接进行算术交叉的问题,统一在执行纵向交叉操作前对个体的每一维进行归一化处理。并且每次纵向交叉操作时产生一个子代维,其目的是在确保其他正常维不被破坏的前提下,给陷入局部最优的维提供机会摆脱维局部最优。假定粒子X(i)的第d1维和d2维进行纵向交叉,其具体操作如下:

式中:MSvc(i,d1)为父代粒子x(i)的第d1维和第d2维执行纵向交叉后所产生的子代维;x(i,d1)和x(i,d2)分别是父代种群中第i个粒子的第d1维和第d2维。
对比各种启发式算法可以发现,绝大部分收敛过早问题是由于种群局部维停滞不前,称为维局部最优。因此,对差分算法引入纵横交叉算法中的纵向交叉操作,利用纵向交叉所独有的摆脱维局部最优能力,可有效解决差分算法收敛过早的问题,改善差分算法随着迭代进行到一定程度后出现的种群多样性不足缺陷,进一步提高差分算法的收敛速度和全局搜索能力。
3 改进差分算法优化神经网络
3.1 BP神经网络
BP(反向传播)神经网络是一种包含多个隐含层的多层前向反馈式神经网络,常见的BP网络为3层结构,其网络拓扑结构如图2所示,包含输入层、隐含层、输出层,层与层之间的各神经元全连接,同一层之间各神经并无连接。其基本思想是:网络的学习训练过程是由样本数据从输入层输入,途径隐含层处理后传播至输出层,然后对比输出层的实际输出与期望输出,若有误差,则将误差信号以某种形式通过隐含层逐层向前分摊误差,并修正网络的权值和阈值,训练网络的权值和阈值时,总是沿着误差减小的方向前进。即网络的学习训练过程是由信号的正向传播和误差的反向传播周而复始进行所构成,随着学习的逐步深入和误差的逐渐减小,当满足结束条件(误差减少到可接受程度或达到预设迭代次数)时结束学习。
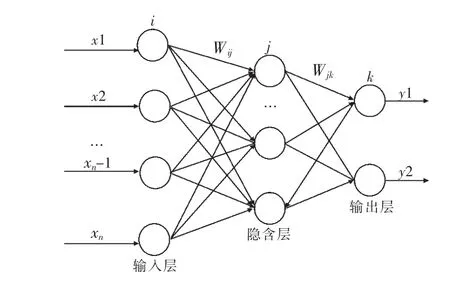
图2 BP神经网络的拓扑结构
3.2 利用IDE算法优化BP神经网络
IDE(改进差分进化)算法凭借其强大的全局搜索和局部探测能力,为解决神经网络在执行BP算法和DE算法训练大规模权值和阈值时遇到的收敛过早、容易陷入局部最小值等问题提供了可能。IDE算法优化BP神经网络的主要目的是利用IDE算法寻找BP神经网络的最优权值和阈值,以降低整个网络的预测误差。在寻优过程中,Wij,Wjk,隐含层的阈值b1j和输出层的阈值b2k在种群中每个个体的编码格式如图3所示。

图3 粒子编码格式
其中:W1为输入层到隐含层之间所有权值组成的排列;W2为隐含层到输出层之间所有权值组成的排列;b1为隐含层所有阈值组成的排列;b2为输出层所有阈值组成的排列。
种群中每个个体的维数为:

式中:n为输入层神经元数;h为隐含层神经元数;m为输出层神经元数。
IDE算法优化神经网络的具体流程如图4所示,执行步骤如下:
(1)由给定的训练样本,选择恰当的神经网络拓扑结构和各层神经元数,并对所有神经元逐个进行实数编码。

图4 IDE优化神经网络参数的算法流程
(2)确定种群规模、最大迭代次数、差分变异概率probability_DE、纵向交叉概率probability _V,并在解空间中随机产生初始种群X。
(3)利用公式(8)对种群X中的每个粒子进行适应度评价。

(4)根据公式(5)计算种群的方差E。若E>MV,则执行DE算法中的突变、交叉、选择操作,将其产生的子代种群保存在矩阵SDE中,然后计算SDE中每个粒子的适应度,并将其与父代种群X中所对应的粒子进行对比,选择适应值更优的粒子作为新的父代粒子保留在X中。若E<MV,则对种群中所有粒子的每一维执行纵向交叉操作,即利用公式(6)并将其产生的子代种群保存在MSvc中,然后计算矩阵MSvc中每个粒子的适应度,并与父代种群X中所对应的粒子进行一一对比,择优保留适应度较好的粒子组成新的父代种群X。
(5)判断是否达到预设的终止条件。若是,则输出此时父代种群X中适应值最好的一组解作为神经网络所对应的权值和阈值。否则,转至(4)进行新的迭代。
3.3 基于混合算法的风速预测
针对风速所固有的随机性、间歇性与非线性等特点,以下采用WPD-IDE-NN算法进行风速预测,并与WPD-BP-NN(混合小波包分解和梯度下降神经网络)算法、WPD-DE-NN(混合小波包分解和标准差分算法的神经网络)算法进行对比。WPD-IDE-NN算法风速预测流程见图5,首先利用WPD将原始风速信号分解成多个不同频率的子序列;然后采用IDE算法优化BP神经网络,并对分解后的各个子序列进行逐个预测;最后叠加所有子序列的预测值,即得到最终预测结果。
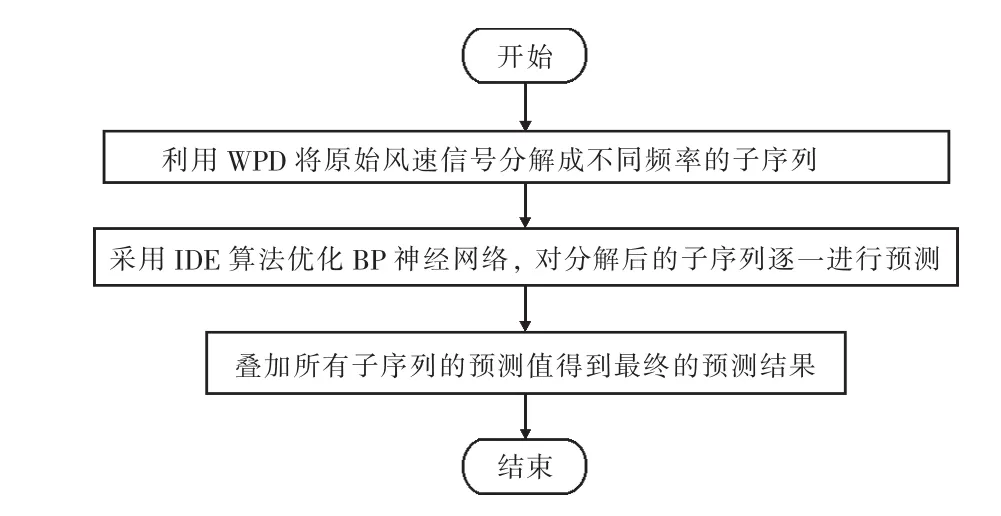
图5 WPD-IDE-NN算法风速预测流程
4 预测结果与对比分析
4.1 预测案例简介
以下结合案例验证所提算法的有效性。图6所示风速序列来源于荷兰某风电场的实测小时风速数据,该图展示了2014年1月测得的风速时间序列(含700个采样点),可被用于单步风速预测。其中,前600个小时的样本数据用于建模,第601~700个数据被作为验证数据。为减少统计误差,所有预测方法均单独执行50次,同时,为确保对比的客观性,所有方法法均采用相同的神经网络,具体网络参数为:输入层、隐含层和输出层所对应的节点数分别为6,8和1;训练代数为100代;学习速率为0.1;目标误差0.01;解空间维数D=(6+1)×8+8+1=65;种群大小M=20;最大迭代次数设为maxgen=1 000。另外,所有方法均将原始风速序列采用WPD形成3层共8个不同频率的子序列,分解后的8个子序列分别为WPD1—WPD8(如图7所示)。

图6 原始风速序列
为更加全面客观地评价各方法的预测准确率,分别采用MASE(平均绝对百分比误差)[15]、RMSE(均方根误差)[4]和MAE(平均绝对误差)[16]对各种方法的预测性能进行评价。
4.2 预测结果对比分析
WPD-IDE-NN,WPD-DE-NN及WPD-BPNN各种算法的误差分析见表1。对比WPD-BPNN与WPD-DE-NN预测结果发现,在相同模型下,WPD-DE-NN算法的各项评价指标均优于传统WPD-BP-NN算法,其中MAPE提高了0.16%,改进幅度为14.82%,这表明采用WPD-DE-NN算法能有效弥补常规WPD-BP-NN算法容易陷入局部最优、泛化能力不足等缺陷。

表1 不同算法的性能对比
另外,WPD-IDE-NN算法的MAPE,RMSE及MAE均明显优于WPD-DE-NN算法,其中,MAPE提高了0.074%,改进幅度为8.3%,这表明对DE算法引进纵向交叉算子能给差分算法提供一种有效的机制,使其在过早出现种群“聚集”现象时,能够跳出维局部最优,从而有效增加种群的多样性,进一步提高了标准差分算法的全局搜索能力。
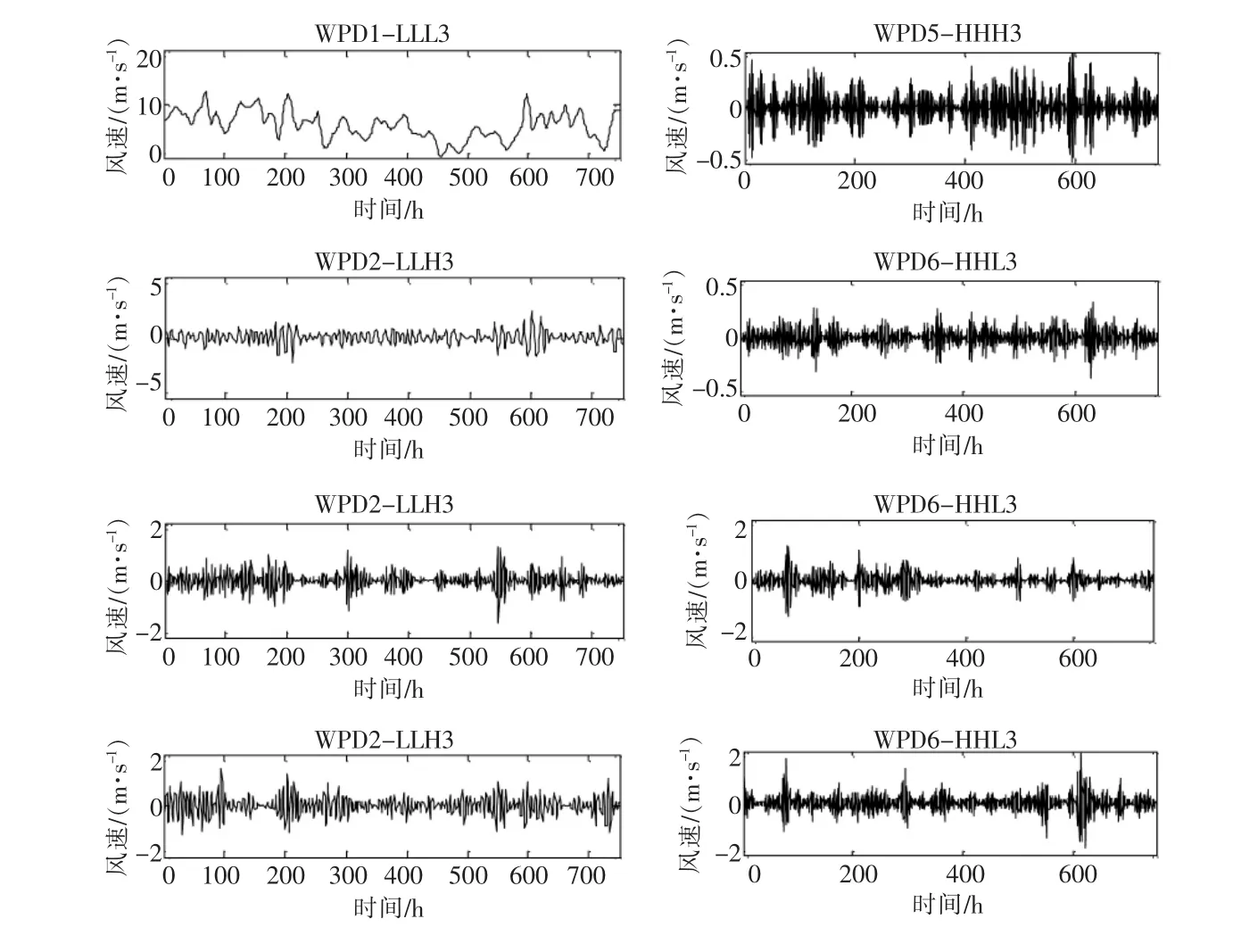
图7 原始风速序列WPD后的子序列
为进一步评价WPD-IDE-NN算法的性能,针对WPD-DE-NN和WPD-IDE-NN所固有的probability-DE(差分变异概率)、probability-v(纵向交叉概率)所带来的性能差异,采取概率以0.1为增量从0.1递增至1的方式,通过100种概率组合更有力地验证了WPD-IDE-NN相比WPD-DENN算法的改进效果。以下仅列出probability_DE从0.1到1,WPD-IDE-NN取最好的probability_v时与WPD-DE-NN的对比(如图8所示)。

图8 改进差分算法在不同差分变异概率下的预测精度对比
由图8可知,WPD-IDE-NN算法在probability_DE下均能取得较好的预测效果,这得益于当迭代达到一定次数、种群的总方差E值趋于0,即出现种群“聚集”现象时,引进纵向交叉算子能有效解决DE算法种群多样性不足的问题,避免陷入局部维最优。
5 结语
针对神经网络在预测过程中所需优化的参数规模较大,导致BP和DE算法在寻优过程中出现收敛速度慢、容易陷入局部最优等现象,提出改进差分算法来优化网络的权值和阈值。利用纵向交叉算子独有的解决局部维最优能力,构建了WPDIDE-NN预测模型。实验证明:
(1)WPD-IDE-NN比WPD-BP-NN和WPDDE-NN算法拥有更高的预测精度,能更有效克服神经网络所固有的缺陷,提高了泛化能力。
(2)通过提出计算种群方差E和引进纵向交叉算子,不仅能够改善随迭代次数增加标准差分算法所固有的“聚集”现象缺陷,促使整个种群搜索朝全局最优方向前进,而且先进行总方差计算,再判断执行差分操作/纵向操作,可有效减少当种群中所有粒子相同时公式(2)中父代差分分量为0所导致的无效操作,有效降低了算法的复杂度,提高了算法的收敛速度。
[1]王德明,王莉,张广明.基于遗传BP神经网络的短期风速预测模型[J].浙江大学学报(工学版).2012,46(5)∶837-841.
[2]全球风力发电市场前景乐观各国竞相开发风能资源[J].浙江电力,2006,25(4)∶46.
[3]黄文杰,傅砾,肖盛.采用改进模糊层次分析法的风速预测模型[J].电网技术,2010,34(7)∶164-168.
[4]王韶,杨江平,李逢兵,等.基于经验模式分解和神经网络的短期风速组合预测[J].电力系统保护与控制,2012,40(10)∶6-11.
[5]CHEN N,QIAN Z,NABNEY I T,et al.Wind Power ForecastsUsingGaussianProcessesandNumerical Weather Prediction[J].IEEE Transactions on Power Systems,2014,29(2)∶656-665.
[6]杨秀媛,肖洋,陈树勇.风电场风速和发电功率预测研究[J].中国电机工程学报,2005,25(11)∶1-5.
[7]孙斌,姚海涛,刘婷.基于高斯过程回归的短期风速预测[J].中国电机工程学报,2012,32(29)∶104-109.
[8]邰能灵,侯志俭,李涛,等.基于小波分析的电力系统短期负荷预测方法[J].中国电机工程学报,2003,23(1)∶45-50.
[9]BASHIR Z A,El-Hawary M E.Applying Wavelets to Short-Term Load Forecasting Using PSO-Based Neural Networks[J].IEEE Transactions on Power Systems 2009,24(1)∶20-27.
[10]KHAJEH M,HEZARYAN S.Combination of ACO-artificial neural network method for modeling of manganese and cobalt extraction onto nanometer SiO2from water samples[J].Journal of Industrial and Engineering Chemistry,2013,19(6)∶2100-2107.
[11]陈海燕,蔡嗣经,郑明贵.中国能源可持续发展的遗传神经网络评价[J].太阳能学报,2010,31(9)∶1220-1224.
[12]ZHUO L,ZHANG J,DONG P,et al.An SA-GA-BP neural network-based color correction algorithm for TCM tongue images[J].Neurocomputing,2014,134(9)∶111-116.
[13]郑一鸣,孙淑莲,孙翔,等.基于自适应小波分析的在线油色谱数据预处理方法[J].浙江电力,2016,35(11)∶1-6.
[14]戈剑武,祁荣宾,钱锋,等.一种改进的自适应差分进化算法[J].华东理工大学学报,2009,35(4)∶600-605.
[15]孟安波,卢海明,胡函武,等.混合小波包与纵横交叉算法的风电预测神经网络模型[J].太阳能学报,2015,36(7)∶1645-1651.
[16]杨锡运,孙宝君,张新房,等.基于相似数据的支持向量机短期风速预测仿真研究[J].中国电机工程学报,2012,32(4)∶35-41.
[17]CADENAS E,RIVERA W.Wind speed forecasting in three different regions of Mexico,using a hybrid ARIMAANN model[J].Renewable Energy,2010,35(12)∶2732-2738.
Short-term Wind Speed Forecast Method Based on WPD-IDE-NN
HUANG Yondong1,CHEN Dongfeng1,XIAO Jianhua1,LIN Yicheng2,DONG Zhen2
(1.Jieyang Power Supply Bureau of Guangdong Power Grid Corporation,Jieyang Guangdong 522000,China;2.College of Automation,Guangdong University of Technology,Guangzhou 510006,China)
Wind speed forecasting is of great importance for intelligent wind farm management power system integration safety.Wind speed forecast is characterized by inherent volatility,intermittence and nonlinearity; in addition,the conventional back propagation(BP)neural network and differential evolution(DE)neural network tend to fall into local optimal which leads to premature convergence and weak generalization ability.The paper presents a short-term wind speed forecast method based on neural network,which combines wavelet packet decomposition(WPD)with improved differential evolution(IDE).Firstly,WPD is employed to decompose the wind speed time series into sub-series with different frequencies.Secondly,the IDE optimized neural is used for single-step prediction of the sub-series.The eventual predicted results are obtained through sub-series aggregation.To verify the proposed method,it is respectively compared with the wind speed forecasting method based on neural networks that adopts hybrid WPD and wind speed forecasting method based on DE that adopts hybrid WPD.Experimental simulation is conducted on actual wind speed data in a specific area,which demonstrates that forecast accuracy of the proposed method is comparatively higher.
differential evolution;wavelet packet decomposition;wind speed forecasting;neural network
10.19585/j.zjdl.201706001
1007-1881(2017)06-0001-07
TP183;TM614
A
2017-03-14
黄勇东(1970),男,工程师,从事电网规划、建设等方面的管理工作。
(本文编辑:方明霞)
广东省科技计划项目(2016A010104016);广东电网公司科技项目(GDKJQQ20152066)
——基于人力资本传递机制
——基于反向社会化理论的实证研究
——基于子女数量基本确定的情形

