基于支持向量机模型的河南艾滋病发病率预测*
徐学琴,王瑾瑾,马晓梅,刘颖,杨梦利,闫国立,王静思,王守东,徐玉芳,余亚楠,宋婀莉
(1.河南中医药大学,河南 郑州 450046;2.河南中医药大学第二附属医院,河南 郑州 450002;3.中国科学院 生物物理研究所,北京 100101)
基于支持向量机模型的河南艾滋病发病率预测*
徐学琴1,王瑾瑾1,马晓梅1,刘颖1,杨梦利1,闫国立1,王静思2,王守东1,徐玉芳1,余亚楠1,宋婀莉3
(1.河南中医药大学,河南 郑州 450046;2.河南中医药大学第二附属医院,河南 郑州 450002;3.中国科学院 生物物理研究所,北京 100101)
目的 探索适合于河南省艾滋病发病趋势的预测模型,准确、快速地预测未来发病变化趋势,为制定艾滋病预防控制的策略和措施提供参考依据。方法收集河南省2000~2014年艾滋病发病率数据,采用支持向量机模型建立其发病率预测模型。其中2000~2013年发病率数据为训练样本,2014年发病率数据为检验样本。以平均相对误差作为预测效果的评价指标。并用该模型对河南省2015~2019年艾滋病的发病率进行预测。结果建立的支持向量机模型的平均相对误差为0.5512%。经预测,河南省2015~2019年艾滋病的发病率分别为0.85/10万、1.84/10万、1.64/10万、1.30/10万、2.01/10万。结论支持向量机模型有较高的预测精度及较小的预测误差,适用于河南省艾滋病的发病率预测。
艾滋病;支持向量机;河南省;预测;模型
艾滋病(acquired immunodeficiency syndrome,AIDS)是一种全身性免疫缺陷性传染病,是我国重大的公共卫生问题[1]。河南省是我国艾滋病疫情较重的省份之一,人类免疫缺陷病毒感染者人数在全国位居第2位[2-3]。在艾滋病的预防控制中,疾病预测起着非常重要的作用。近年来,学者们探索用不同方法进行艾滋病发病趋势的预测,主要有神经网络、灰色模型及马尔科夫模型等[4-7]。神经网络模型的缺陷是收敛速度慢、易陷入局部极小点,灰色模型和马尔科夫模型普遍存在预测精度低的问题。而支持向量机模型具有很好的泛化能力,在解决小样本、非线性及高维模型识别问题中具有先天的优势,它能有效利用高维特征空间,利用计算机学习理论分析问题,使问题得到最优解[8-9]。
1 资料与方法
1.1 支持向量机的基本原理
支持向量机是基于统计学习理论、研究小样本情况下的机器学习规律的一种方法,以结构风险最小化为思想,在使样本训练误差最小化的同时又缩小模型泛化误差的上界,从而提高模型的泛化能力[10]。它被广泛用于模式识别、分类、回归、图像分析、药物设计及食品质量控制等方面[11]。在疾病预测方面主要利用的是支持向量机的回归算法,该方法可以将非线性问题通过非线性变换映射到某个高维特征空间,在高维空间中完成线性回归,求得最优分类面。在分类面中引入合适的核函数可以代替高维空间中复杂的内积运算,从而实现线性回归。
1.2 方法
1.2.1 预测方案及数据的预处理 本研究采用的预测方案为数据序列预测,即把河南省艾滋病的年发病率看作连续的时间序列,其变化规律已蕴含于其中。采用支持向量机建立起反映该变化规律的模型,从而对未来数据进行预测。因此,建立模型需获得河南省艾滋病的历史发病率数据,该数据主要来源于河南省卫生统计年鉴及河南省统计局。
为避免因为输入输出数据差别而造成预测误差较大,需对数据进行归一化处理,把所有数据都转化为0~1之间的数值[12]。峰值法是常用归一化方法之一,即用每年的艾滋病发病率除以比每个数据都大的1个数据,该数据即为峰值。
1.2.2 参数的确定 核函数的引入避免复杂的高维运算,其在支持向量机中是解决非线性问题的关键,是由线性到非线性之间的桥梁[13]。常用的核函数有多项式核函数、高斯径向基核函数及多层感知器核函数等。本研究中采用的是高斯径向基核函数,其宽度取值为0.25。惩罚因子C=20,ε不敏感函数取值为0.00001。
1.2.3 模型的训练及仿真预测 以2000~2013年的发病率数据来训练模型,以2014年的发病率数据来检验模型,采用新陈代谢预测法。即以每3年的发病率数据构成1个原始时间序列,预测第4年的发病率,而每当新加入1个数据,则舍弃原来序列最前端1个数据。预测的效果以相对误差的绝对值来评价,即(预测发病率-实际发病率)/实际发病率×100%。所得预测值需进行反归一化处理,即预测值×峰值。以上运算在Matlab 7.0软件中实现。
2 结果
利用所建立的模型对2003~2014年的发病率进行仿真预测。其平均预测误差为0.5512%,其中训练样本的平均预测误差仅为0.0033%,预测值和真实值吻合度非常高,预测误差较小。检验样本处的实际发病率为3.05/10万,预测发病率为2.85/10万,相对误差为6.5784%,较为理想。经该模型预测,河南省2015~2019年的艾滋病发病率分别为0.85/10万、1.84/10万、1.64/10万、1.30/10万、2.01/10万。见附表和附图。
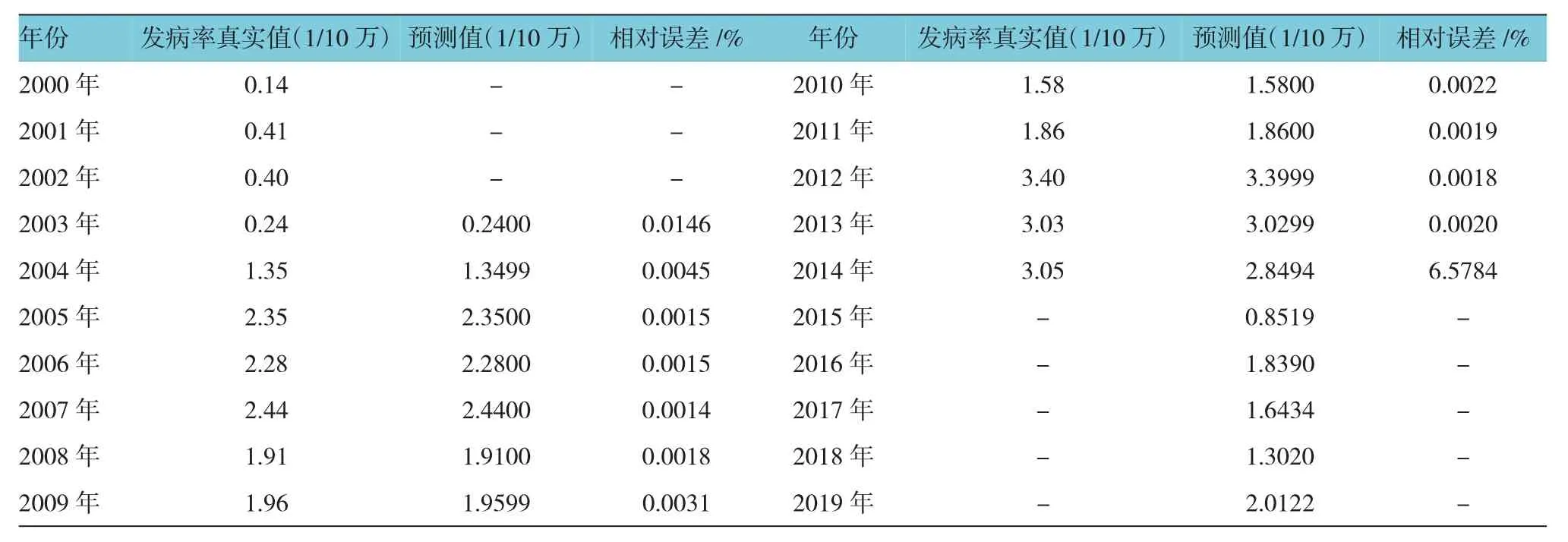
附表 河南省艾滋病发病率的真实值、预测值(反归一化)及相对误差绝对值

附图 河南省艾滋病实际发病率与预测发病率曲线
3 讨论
对于艾滋病的流行趋势来说,其影响因素错综复杂,包括人口、经济、行为及环境等。目前,我国尚没有充分开展艾滋病相关影响因素数据资料的监测和收集,因此,通过分析各影响因素来建立艾滋病的预测模型比较困难。而影响因素的综合作用却反映在了历史发病率数据当中,因此通过分析艾滋病的历史年发病率数据来建立预测模型,预测其未来发生发展趋势可行。在众多预测模型中,支持向量机模型的主要优势在于:其建立在结构风险最小化的原则上而不是基于错误率,且能在极小的训练样本下表现出极高的分类稳定性[14]。该模型可将变量集映射到高维特征空间中并进行正确区分,以解决小样本、非线性及低维空间不易区分的难题[15]。因此,本研究采用支持向量机模型来建立河南省艾滋病的发病率预测模型。
所建立的模型在仿真预测样本点的平均相对误差为0.5512%,检验样本的预测误差为6.5784%,尤其在训练样本处的平均预测误差仅为0.0033%,均满足中期预测(1~5年预测期)相对误差控制在10%~20%的要求[16]。该模型的建立能够为及时、准确预测河南省艾滋病发生发展趋势,为制定河南省艾滋病的预防控制提供理论参考。经该模型预测,河南省在2015~2019年的发病率呈现为先下降后上升的趋势,仍然保持在较高的发病水平,因此,对河南省艾滋病的监测、预防工作仍需加强。
[1]郭金玲.艾滋病对河南社会经济影响的研究[D].武汉:华中科技大学,2007.
[2]赵秀哲.社会学视野下的河南艾滋病流行传播[J].企业家天地(下旬刊),2010(9):243-245.
[3]刘佳,杨文杰,闫江舟,等.河南省四地区一线艾滋病抗病毒治疗失败的耐药分析[J].中华实验和临床病毒学杂志,2015,29(6):532-536.
[4]颜康康,林雪君,鲍红红,等.灰色GM(1,1)模型在艾滋病、淋病、梅毒发病率预测研究中的应用[J].实用预防医学,2015,22(3):371-374.
[5]罗静,杨书,张强,等.时间序列ARIMA模型在艾滋病疫情预测中的应用[J].重庆医学,2012,41(13):1255-1256.
[6]张夏燕,邢健男,钱莎莎,等.Markov模型在艾滋病研究领域中的应用[J].中华流行病学杂志,2014(5):606-609.
[7]YU H K,KIM N Y,KIM S S,et al.Forecasting the number of human immunodeficiency virus infections in the korean population using the autoregressive integrated moving average model[J].Os ong Public Health and Research Perspectives,2013,4(6):358-362.
[8]JEDLINSKI L,JONAK J.Early fault detection in gearboxes based on support vector machines and multilayer perceptron with a continuous wavelet transform[J].Appl Soft Comput,2015(30):636-641.
[9]李娟,吴疆,卢莉,等.基于支持向量机建立环境和遗传因素对2型糖尿病的预测模型[J].中华疾病控制杂志,2012,16(2):171-175.
[10]李海生.支持向量机回归算法与应用研究[D].广州:华南理工大学,2005.
[11]GAO K,XI X J,WANG Z,et al.Use of support vector machine model to predict membrane permeate flux[J].Desalination and Water Treatment,2016,57(36):16810-16821.
[12]周文明,陈军生,宋吉星,等.基于支持向量机的装备技术准备能力预测算法[J].系统工程与电子技术,2013,35(9):1903-1907.
[13]孙德山.支持向量机分类与回归方法研究[D].长沙:中南大学,2004.
[14]高昭昇,曹晋军,冯柳,等.基于大数据的传染病爆发、预测和预警等应用分析[J].中国卫生事业管理,2016,33(4):270-272.
[15]吴宏进,许家佗,张志枫,等.基于数据挖掘的围绝经期综合征中医证候分类算法分析[J].中国中医药信息杂志,2016,1:39-42.
(李科 编辑)
Forecast of incidence of AIDS in Henan Province based on support vector machine*
Xue-qin Xu1,Jin-jin Wang1,Xiao-mei Ma1,Ying Liu1,Meng-li Yang1,Guo-li Yan1,Jing-si Wang2,Shou-dong Wang1,Yu-fang Xu1,Ya-nan Yu1,E-li Song3
(1.Henan University of Traditional Chinese Medicine,Zhengzhou,Henan 450046,China;2.The Second Affiliated Hospital,Henan University of Traditional Chinese Medicine,Zhengzhou,Henan 450002,China;3.Institute of Biophysics,Chinese Academy of Sciences,Beijing 100101,China)
ObjectiveTo explore a model for forecasting acquired immunodeficiency syndrome (AIDS)in Henan Province,and accurately and quickly predicting the future trend of AIDS,so as to provide reference for AIDS prevention and control.MethodsData of AIDS incidence in Henan Province from 2000 to 2014 were collected.The incidence prediction model was established using support vector machine.The data from 2000 to 2013 were taken as training samples,and the data of 2014 were used as testing sample.Average relative error was used to evaluate the effect of prediction.Then the model was utilized to predict the incidence of AIDS in Henan Province from 2015 to 2019.ResultsThe average relative error of the established support vector machine model was 0.5512%.It is predicted that the incidences of AIDS in Henan Province from 2015 to 2019 are 0.85/105,1.84/105,1.64/105,1.30/105and 2.01/105respectively.ConclusionsSupport vector machine model has high prediction accuracy and small error,and is suitable for AIDS prediction in Henan Province.
acquired immunodeficiency syndrome;support vector machine;Henan Province;prediction;model
R181.2
A
10.3969/j.issn.1005-8982.2017.12.019
1005-8982(2017)12-0093-03
2016-09-21
河南省软科学研究重点项目(No:102400440002);河南省2010年科技发展计划(No:102400440002)
闫国立,E-mail:yanguoli0371@126.com

