表面驻泡颗粒在液相运动中的特征分析❋

栾 健， 张 继， 梅 宁

(中国海洋大学工程学院，山东 青岛 266100)

表面驻泡颗粒在液相运动中的特征分析❋

栾 健， 张 继， 梅 宁❋❋

(中国海洋大学工程学院，山东 青岛 266100)

基于多相流体动力学的贝赛特(Basset)-鲍瑟内斯克(Boussinesq)-奥森(Ossen)方程(BBO方程)研究滑移条件下颗粒在两相流中的运动情况。针对小型浮游生物表面微结构特征建立固-气-液三相双滑移模型，运用Karman边界层动量定理推导出以气相衔接的固-气相和气-液相层流边界层速度分布表达式。通过参数分析法确定Basset力、颗粒所受阻力及附加质量力对颗粒运动的影响，对BBO方程进行简化求解，得到颗粒在流场中的轨迹方程。将本文提出的滑移速度分布代入轨迹方程得到有滑移边界条件下颗粒在流场中的运动速度随时间的变化。通过分析可以得到，颗粒表面的驻泡结构使得颗粒与流场接触界面处出现速度滑移，从而提高了颗粒的运动速度。

驻泡颗粒；固-液-气三相；边界滑移；BBO方程；运动轨迹

符号表

在海流作用下，超微型浮游生物会在浸海材料表面形成一层生物黏膜，并与浸海材料一道释放出化学物质(化学踪迹)，随后浮游生物幼虫极易附着上去并长大，从而形成生物污损，影响海洋能装置的相关生产活动[1]。采用间歇性释放氯气和涂料防止海洋生物附着虽然有效，但引发的环境问题一直备受争论。由于小型浮游生物系统自身存在复杂性、多样性，同时在其运动过程中涉及物理过程和生物过程间的交互作用，海洋浮游生物的输运行为的理论解释还不全面[2]。因此，浮游生物在浸海材料壁面附近的扩散和质迁移机理研究成为防止浸海材料海洋生物附着新一代技术的基础课题。

对于颗粒物在两相流中的受力情况，目前大多采用数值模拟方法进行研究。Hu等[3]最先采用有限元ALE方法对颗粒两相流进行数值模拟，但由于计算量大,而只用于一个或几个颗粒的两相流动，最开始采用隐式方法不稳定，后经过算法改进可以模拟颗粒在黏弹性流体中的运动。由长福等[4]采用数值模拟方法计算了煤粉颗粒所受的Magnus力，考虑颗粒旋转速度、流动Re数对Magnus力的影响。孙光明、陈臻采用CFD方法对球形颗粒沉降轨迹进行数值模拟，得到与实验相符的单颗粒沉降在近壁面的转动特点，当颗粒与流体的相对速度较大时会产生尾涡，其涡的脱落、配对对流场有很大影响[5-7]。Gan等[8]在数学模型中引入能量方程，使得有限元ALE方法可以对热对流条件下颗粒两相流问题进行研究。仝志辉[9]采用有限元ALE方法对换热条件下不同固液密度比范围内的非等温颗粒的沉降运动进行数值模拟，结果表明热对流对颗粒的影响随着固液密度比的增加而增大热对流使颗粒沉降的发展进程加快，颗粒摆动幅度增大。近年来发展起来的无网格迦辽金(EFGM)具有无需划分网格、精度高、后处理方便、可消除体积闭锁、收敛快等优点[10]，目前也开始用于求解各种流体问题[11-12]。仇轶等[13]采用EFGM法对气固两相流进行直接数值模拟，通过算法研究和求解碰撞问题讨论无网格方法对多相流数值模拟的适用性。在颗粒运动理论研究方面，Tchen在前人研究基础上写出单个小颗粒在无边界影响的均匀紊流场中的运动方程[14]。邵学军[15]利用随机过程的观点和方法研究颗粒物在两相流中的运动情况。综上所述，可以看出对颗粒物在流场中的输运过程主要采用数值模拟方法，在机理研究方面较为薄弱，同时，在有滑移边界条件基础上的颗粒输运机理研究更为少见，所以，对于颗粒物在流场中的输运机理的理论研究仍需引起极大重视。

本文基于小型浮游生物表面微结构，建立固-气-液三相边界层双滑移模型，通过边界层滑移速度修正边界条件，运用Karman边界层动量定理推导出以气相衔接的固-气相和气-液相层流边界层速度分布表达式。并通过BBO方程建立颗粒与流场之间的耦合关系，采用参数方法对BBO方程进行简化求解，得到颗粒在均匀流场中的运动轨迹。通过双滑移边界层速度分布对轨迹方程进行修正，得到滑移边界条件下颗粒在流场中的运动轨迹。为后期小型浮游生物水平输运行为的实验研究提供一定理论指导。

1 颗粒在固液两相流中运动的模型描述

自然界存在一些生物利用纳米结构表面超疏水性，使得其表面具备特殊的物理性质，最常见的是荷叶的自清洁效应。小型海洋浮游生物表面存在凹凸不平的微纳米结构[16-17]，当流场经过浮游生物表面时，其表面有些会形成疏水膜[18-20]，在生物膜与流体之间会驻留微气泡[21-23]。图1是疏水表面与流体之间驻留气泡的图片，图2是根据疏水表面存在微气泡的原理描述的颗粒表面驻泡现象示意图[24-25]。这种特殊微纳米结构在其扩散和迁移过程中起到重要作用。通过分析这驻泡微结构在浮游生物输运过程中的作用，可以为防止浸海材料海洋生物附着的机理研究提供新的理论思路。

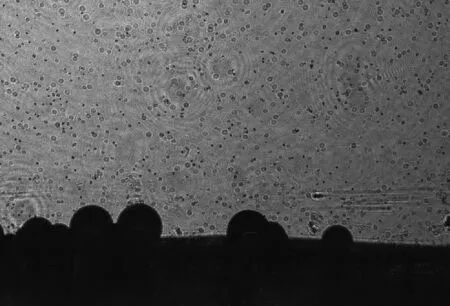
图1 疏水表面驻泡现象

图2 颗粒表面微纳米凹痕结构简图

本文以小型浮游生物表面微结构为基础建立固-气-液三相双滑移模型(见图3)。当颗粒在流体中运动时，在流场的剪切力带动下，颗粒固体表面会与微气泡之间产生边界滑移，与此同时，微气泡与流场也会产生边界滑移，从而产生双滑移效果。采用边界层滑移速度对Navier边界条件进行修正，进而可得到双滑移边界条件下颗粒表面边界层内流场速度分布。此模型在以下假设中建立：

(1)颗粒在低雷诺数的均匀流场中流动

(2)流场为黏性，不可压流体

(3)颗粒表面微气泡小于固-液相边界层厚度(4)颗粒为球形颗粒，其表面微气泡为理想气体，无黏性

(5)颗粒在流场中初始位置为0，初始速度为0

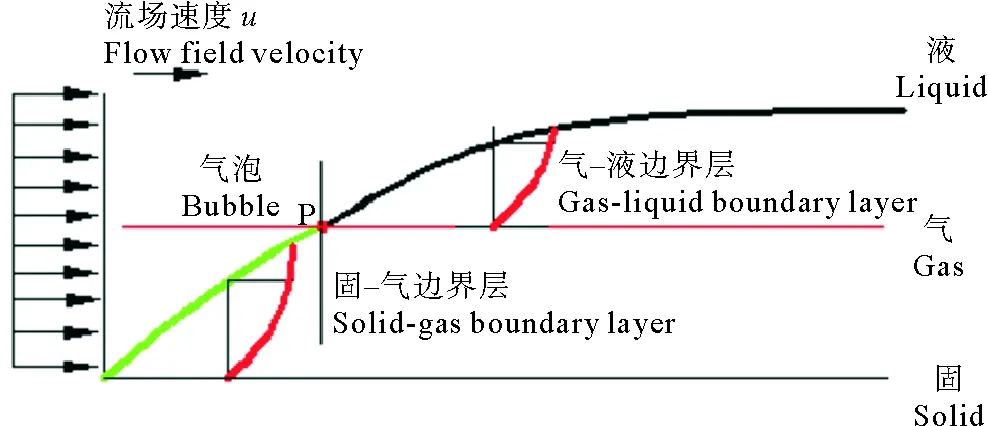
图3 颗粒在固液两相流中的物理模型

2 固-气-液三相层流边界层内双滑移速度分布理论计算

为确定边界层中的特征量，关键在于合理给出边界层中的无量纲速度分布函数F(η)，针对层流流动，将固-气相边界层假设为经典多项式速度分布，气-液相边界层假设为指数型速度分布，将速度分布代入边界层动量方程后，可解得边界层厚度、任意点流速、摩擦阻力系数等。作者在文献[26]的研究中已经对各相边界层分布做了分析，现将研究结果表示如下：

2.1 确定固-气相层流边界层分布

固-气相滑移模型基于小型浮游生物表面微结构，采用边界层理论中经典的三项速度多项式和四项速度多项式的线性组合，以平板边界层积分方程为基础，推导得到固-气相层流边界层速度分布多项式[26]：

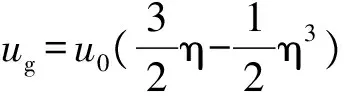
(1)

2.2 确定气-液相层流边界层分布

2.2.1 微气泡与边界滑移的关系 根据Navier边界条件定义，滑移速度的意义为按照主流区速度分布的虚拟延长而在边界上获得的速度值，因此滑移长度为速度分布在边界处的线性延长至速度为0的位置与流动边界的距离[27]，最终得到无量纲滑移长度为：

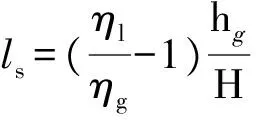
(2)

2.2.2 气-液相层流边界层速度分布 液体做层流流动，根据Karman边界层动量方程的层流速度分布方程，采用指数型方程形式进行求解：

ul=AηeBη2。

(3)

设定边界条件：

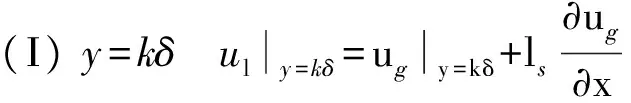
由上述边界条件，得到系数A、B：

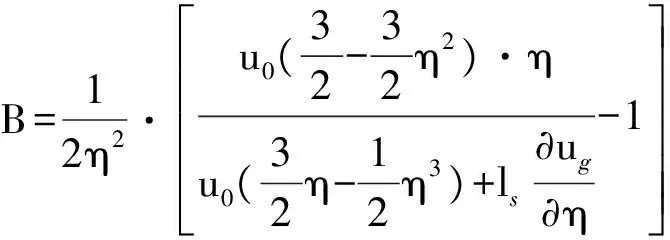
(4)

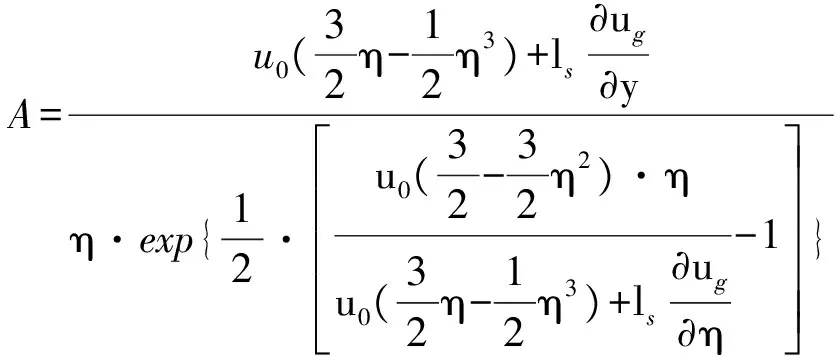
(5)

2.3 气-液相层流边界层速度分布参数分析

为计算固-气相和气-液相层流边界层的速度分布，需要设定初始条件如表1：

表1 初始参数设计

Note:①Bubble height；②Water viscosity；③Air viscosity；④Two-dimensional system characteristic length；⑤Initial flow velocity

根据已设计的数据，计算得到气-液相速度分布的系数值分别为：

A=0.206，B=-0.499。

最终得到固-气相层流边界层的速度分布为经典形式：

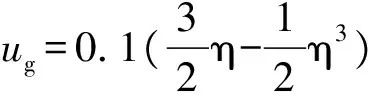
(6)

气-液相层流边界层的速度分布：

u1=0.206ηe-0.499η2。

(7)

3 颗粒在固液两相流中运动的模型描述

3.1 颗粒在固液两相流中的受力分析

任意流场条件下颗粒物均受到不同方向的作用力(见图4)。其中包含与流体和颗粒间的相对运动无关的力，包括压力梯度力、重力及浮力；依赖于流体和颗粒间的相对运动且作用力方向与相对运动速度方向相反的力，包括Stokes力、虚拟质量力和Basset力；还有依赖于流体和颗粒间的相对运动但作用方向与相对运动速度方向垂直的力，如Saffman力和Magnus力。

3.2 BBO基本方程

颗粒受力分析对固液两相流中颗粒运动的研究十分关键。Stokes(1851)曾对单个球体、圆柱体积无限长板在粘性流体中的简谐直线运动做了系统研究，并给流体与颗粒关系的表达式。此后，Basset(1888)、Boussineaq(1885)、Oseen(1927)等研究了单个球形颗粒在黏性流体中的运动，得出球形颗粒的受力不仅受瞬时速度和加速度作用，更与颗粒加速运动的历史有关，继而得到著名的BBO方程。

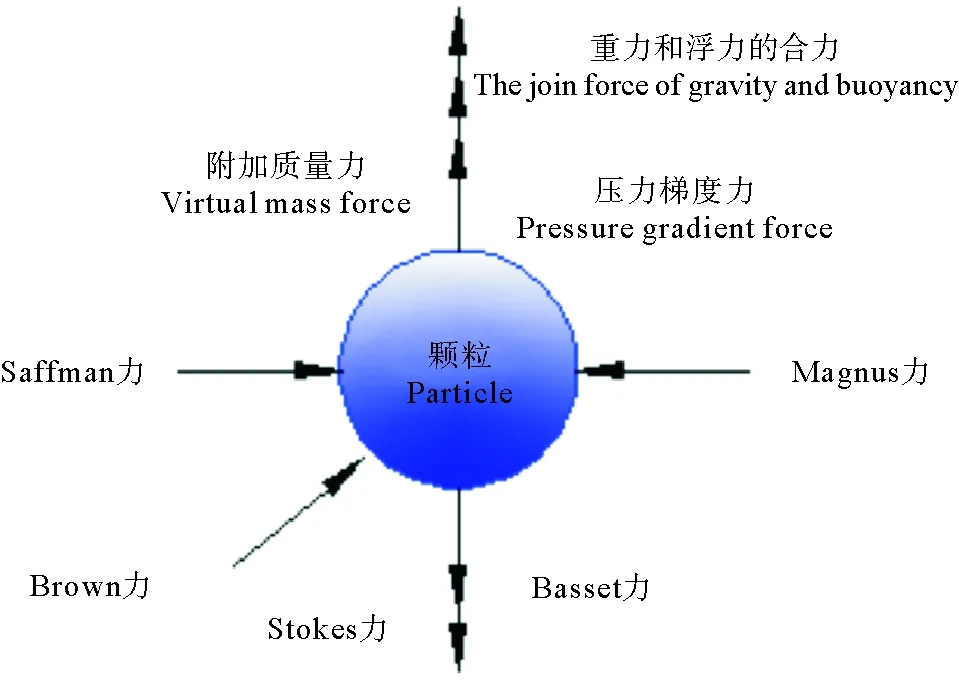
图4 颗粒在固液两相流中的受力模型

在BBO方程基础上，颗粒在均匀流场中的运动过程可表示为[29]：

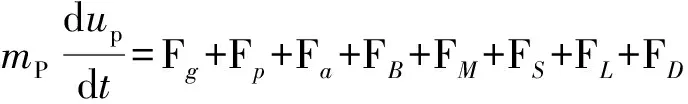
(8)

由于均匀流场中，流场速度梯度不大，所以压力梯度力可以省略；考虑球形颗粒在流场中不易计入颗粒的旋转和侧向运动特征，所以可以忽略升力，Magnus力和Saffman力的作用。有效重力只与颗粒的粒径大小有关，与颗粒运动无关，所以此处主要研究与颗粒运动紧密相关的力：Basset力、颗粒所受阻力以及附加质量力。

3.2.1 Basset力计算 在两相流中，当颗粒与流体的相对速度有加速度存在时，颗粒会受到非恒定的气动力作用，即附加质量力和Basset力。Basset力是由于相对速度随时间的变化而导致颗粒表面附面层滞后所产生的非恒定气动力，由于该力大小与颗粒的运动经历有直接关系，所以该力又称为“历史力”[30]。

Basset力的一般表达式[31]

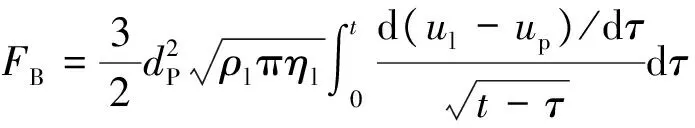
(9)

Basset力的物理意义表征颗粒相对流体作非恒定运动时受到的附加黏性力的时间积分。实际工程中，颗粒相对流体的运动速度及其对时间的导数是待求量，Basset力表达式中被积函数部分未知，极难得到直接解，因此采用数值分析方法进行求解。

根据被积函数未知项的物理意义，设d(ul-uP)/dτ=g(τ)，若g(τ)用时间τ的n次多项式来逼近，则可表示实际颗粒相对流体做变速运动。令

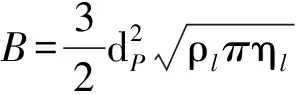
(10)

g(τ)=Kτn。

(11)

本文采用等步长复合梯形公式进行计算，将积分区间分为两部分，以消除积分的奇异性，即：

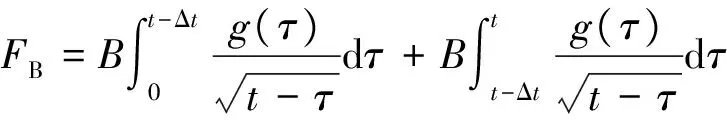
(12)

其中Δt=t/n是积分步长，n是子区间数。将公式第二项进行变形：

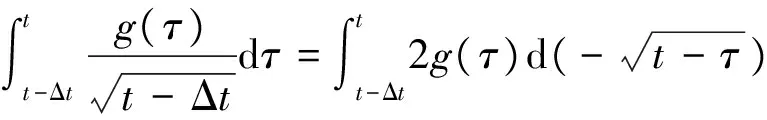
(13)

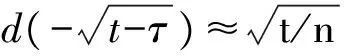
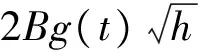
(14)

其中h=Δt=t/n，h的大小由给定的计算精度决定，与积分上限t有关。

3.2.2 单个颗粒所受阻力的计算 在均匀流场中，颗粒会受到重力以及流体对颗粒运动阻力(曳力)的作用。当不同粒径的颗粒同时运动时，颗粒之间的碰撞需要加以考虑。本文主要考虑单个颗粒在流场中的运动特性，所以单个颗粒在流场中所受的阻力公式[32]:

FD=3πηldPf(ul-uP)，

(15)

其中：

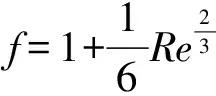
(16)

3.2.3 附加质量力的计算 附加质量力的产生来自于颗粒周围流体的加速运动，当颗粒相对流体做变速运动时，颗粒将会带动周围流体作相同加速度的非恒定运动，并且这些被加速的流体体积恰好等于颗粒体积的一半，其公式可以表示为[23]：

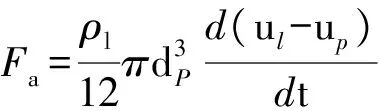
(17)

3.3 颗粒在两相流中受力分析

本文采用参数分析方法，比较直观得到对颗粒运动轨迹影响较大的力，从而对颗粒在两相流中运动的BBO控制方程进行简化，最终得到颗粒在均匀流场中的运动方程。定义速度的松弛时间为颗粒与流体之间松弛过程的快慢，则有：

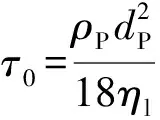
(18)

颗粒物和液体的物性参数如表2。

根据物性参数值，设未知被积项g(τ)=τ3，说明颗粒此时相对流体作非周期变加速运动。采用数值方法得到Basset力，相间阻力以及附加质量力的数值解，并用数值方法进行比较(见图5)。

表2 物性参数

Note：①Water viscosity；②Water density；③Particle density；④Particle radius；⑤Temperature

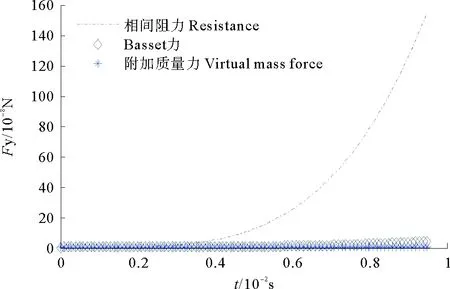
图5 颗粒在运动过程中各主要作用力随时间的变化趋势

从图5中可以看出在对颗粒运动影响较大的各项作用力中，Basset力和附加质量力相对于颗粒所受阻力来说比较小，为简化颗粒运动的BBO方程，在以后的计算中可以忽略。

4 颗粒在均匀流场中运动轨迹方程确定

利用BBO方程表达均匀流场中颗粒的运动过程，即[33]：

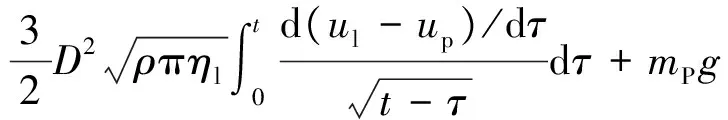
(19)

根据上文受力分析，忽略控制方程第一项压力梯度项、第三项虚拟质量力项和Basset力项，引入松弛时间τ，最终简化得到：

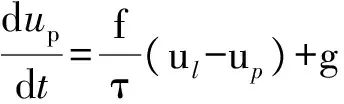
(20)

设颗粒在初始时刻的轨迹位置为0,初始速度为0，设水的流速ul保持不变，求解微分方程(4)可得颗粒位移公式为：

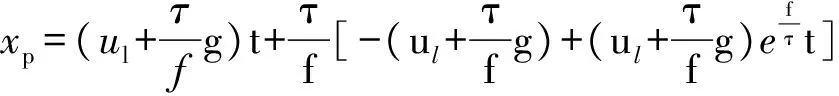
(21)

将本文提出的有滑移层流边界层内速度分布公式代入式(21)，得到有滑移条件下颗粒表面边界层的流场速度分布：

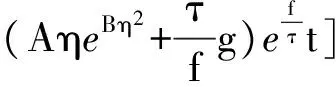
(22)

将本文参数分析得到的固-气-液三相边界层内速度分布数值表达式代入式(22)，得到有滑移边界条件下，一定边界层厚度处，颗粒随时间的运动轨迹(见图6)。

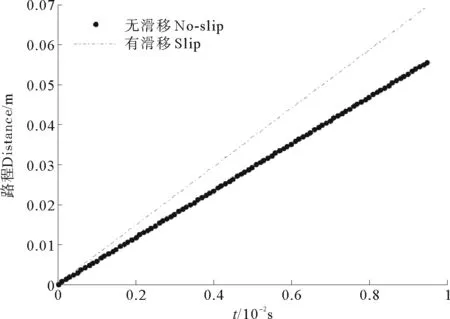
图6 颗粒随时间变化的运动轨迹

由图6可以看出，根据本文设计的初始参数，初始静止的颗粒在较低流速的流场中的运动轨迹随时间成线性变化。在双滑移边界条件的基础上，有滑移时颗粒表面边界层内流场速度比无滑移时大，从而有滑移条件下颗粒运动速度相应较大。当流场经历颗粒表面微气泡时，微气泡会产生局部减阻的效果，从而使流场速度有明显增大。因此相同时间内，表面驻泡颗粒运动速度增大，颗粒运动路程较大。

5 结语

本文以小型浮游生物在海洋流中的输运过程为基础，针对浮游生物表面微气泡结构建立固-气-液三相双滑移模型，通过边界层滑移速度修正边界条件，运用Karman边界层动量定理推导出以气相衔接的固-气相和气-液相层流边界层速度分布表达式。以双滑移边界层速度分布为基础，采用BBO方程研究颗粒与流体之间的耦合作用，得到颗粒在固液两相的运动轨迹。通过理论分析，颗粒在均匀流场中的运动随时间基本呈线性变化，在双滑移边界条件的基础上，有滑移时颗粒表面边界层内流场速度较大，相同时间内颗粒运动路程较大。

本文从理论上推导滑移条件下，球形颗粒在固液两相流中的运动轨迹，采用BBO方程对颗粒与流体的耦合作用进行研究。后期将会设计实验对本文的理论进行验证，同时会深入研究颗粒自身因素，环境因素等对影响颗粒运动的影响，为颗粒在两相流中的耦合分析提供一定的理论思路，为小型浮游生物的输运过程研究开拓新途径，从而促进海洋能源的开发利用，增强对海洋环境的保护。

[1] GAO Yunhua, FU Yubin, “Compositon and variation of bacterial-films on immerge-seawater-material-surfaces and their influences on attachment of halobios”, Marine Enirment Science, 2001, 20(2): 51-55.

[2] 韩怡昉. 静止环境中微尺度物体的输运机理 [D]. 青岛: 中国海洋大学, 2014. Han Y. F, Mechanism Study into the Transport Process of Micro-object in Static Fluid System[D]. Qingdao: Ocean University of China, 2014.

[3] Hu H H, Joseph D D, Crochet M J. Direct simulation of fluid particle motions[J]. Theoretical and Computational Fluid Dynamics, 1992, 3: 285-306.

[4] 由长福, 祁海鹰, 徐旭常. 煤粉颗粒所受Magmis力的数值模拟[J]. 工程热物理学报, 2001, 22: 625-628. You C F. Numerical simulation of magnus lift on a coal particle[J]. Journal of Engineering Thermophysics, 2001, 22: 625-628.

[5] 孙光明. 圆球粒子沉降的数值模拟及实验研究[D]. 浙江大学, 2006. Sun G M. Experimental Research and Dynamic Simulation of Sphere Motion[D]. Hangzhou: Zhejiang University, 2006.

[6] 陈臻. 应用分布式拉格朗日乘子/虚拟区域法对颗粒两相流的直接数值模拟[D]. 浙江大学, 2006. Chen Z. Directnumerical Simulation for Partieulate Flows with Distributed Lagrange Multiplier/fictitious Domain Method[D] Hangzhou: Zhejiang University, 2006.

[7] 吕红. 方形颗粒两相流的直接数值模拟[D]. 重庆: 重庆大学, 2011. Lv H. Direct Numerical Simulation of Rectangular Particle-Liquid two-phase Flow[D]. Chongqing: Chongqing University, 2011.

[8] Gan H, Chang J Z, Feng J J, et al. Direct numerical simulation of the sedimentation of solid particles with thermal convection[J]. Journal of Computational Physics, 2001, 169: 427-462.

[9] Belytschko T, Krougauz Y, Organ D, et al. Meshless method: An overview and recent developments[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139: 3-47.

[10] Belytschko T, Lu Y Y, Gu L. Element-free Galerkin methods[J]. International Journal for Numerical Methods in Engineering, 1994, 37: 227-256.

[11] Lin H, Atluri S N. The meshless local Petrov-Galerkin method (MLPG) for solving incompressible Navier-Stokes equations[J]. Computer Modeling in Engineering &Sciences (CMES), 2001, 2: 117-142.

[12] Han Y Y, 李大鹏. 汽-液两相交界面直接数值模拟的无网格数值方法[J]. 国外核动力, 2001, 2: 35-44. Han Y Y, Li D P. Meshless numerical method for direct numerical simulation of gas-liquid two intersection boundary interface[J]. Foreign Nuclear Power, 2001, 2: 35-44.

[13] 仇轶, 由长福, 祁海鹰等. 用无网格伽辽金法模拟流场中的颗粒运动[J]. 化学学报, 2006, 57(6): 1323-1328. Yi Q, You C, Haiying Q I, et al. Direct numerical simulation of gas-particle flows using EFG method[J]. Journal of Chemical Industry & Engineering, 2006, 57(6): 1323-1328.

[14] Tchen, C M. Mean value and correlation Problem connected with the motion of small Particles suspended in a turbulent fluid, 1947, 4.

[15] 邵学军, 夏震寰. 悬浮颗粒紊动扩散系数的随机分析[J]. 水利学报, 1990, 10(10), 36-40. Shao X. Stochastic analysis of the turbulent diffusion coefficient for sediment particles[J]. Journal of Hydraulic Engineering, 1990, 10(10), 36-40.

[16] Chiovitti A, Dugdale T M, Wetherbee R. Diatom adhesives molecular and mechanical properties[J]. Biol Adhes, 2006, 56(2): 79-103.

[17] 张前前, 陈然, 李琛. 基于海洋硅藻三维结构的微纳米材料研究进展[J]. 中国海洋大学学报(自然科学版), 2012, 42: 137-142. Zhang Q Q, Chen R, Chen L I. Research Advances of the Micro/Nanomaterials Basing on the Three-Dimensional Structures of Marine Diatoms[J]. Periodical of Ocean University of China, 2012, 42: 137-142.

[18] Hecky R, Mopper K, Kilham P, et al. The amino acid and sugar composition of diatom cell-walls[J]. Mar Biol, 1973, 19: 323-331.

[19] Crawford S A, Higgins M J, Mulvaney P, et al. Nanostructure of the diatom frustule as revealed by atomic force and scanning electron microscopy[J]. J Phycol, 2001, 37: 543-554.

[20] 曹杉. 海洋底栖硅藻附着机理及其防污技术研究[D]. 北京: 清华大学, 2013. Cao S. Research on Adhesion Mechanism and Antifouling Technologies of a Marine Benthic Diatom[D]. Beijing: Tsinghua University, 2013.

[21] J W G Tyrrell, P Attard. Atomic force microscope images of nanobubbles on a hydrophobic surface and corresponding force-separation data[J]. Langmuir, 2002, 18(1): 161-166.

[22] 张雪花, 胡钧. 固液界面纳米气泡的研究[J]. 电子显微学报, 2003, 22(2): 137-140. Zhang X H, Hu J, et al. Studies on nanobubbles formed at solid/liquid interface[J]. Journal of Chinese Electron Microscopy Society, 2003.

[23] Yang S, Dammer S M, Bremond N, et al. Characterization of nanobubbles on hydrophobic surfaces in water[J]. Langmuir, 2007, 23(13): 7072-7077.

[24] 王玉亮. 固液界面纳米气泡与基底相互作用研究及滑移长度测量[D]. 哈尔滨: 哈尔滨工业大学, 2009. Wang Y L. Study of Nanobubble and Substrate Interaction and Measurement of Slip Length at Solid Liquid Interfaces[D]. Harbin: Harbin Institute of Technology, 2009.

[25] 杜亚平. 疏水表面纳米气泡特性及固液边界滑移长度关系研究[D]. 哈尔滨: 哈尔滨工业大学, 2012. DU Y P. The Study on Relationship of the Hydrophobic Surface Nanobubbles Characteristics and Solid-Liquid Boundary Slip Length[D]. Harbin: Harbin Institute of Technology, 2012.

[26] Luan J, Mei N. The mechanism research about micro-bubble resistance reduction in the micro-scale laminar flow[J]. Ocean Engineering, 2015, 109: 14-19.

[27] 王绍亭. karman边界层动量方程中的层流速度分布方程[J]. 天津大学学报, 1989, (2): 121-126 . Wang S. On laminar velocity profile equation in karman boundary layer momentum equation[J]. Journal of Tianjin University, 1989, (2): 121-126.

[28] 曹炳阳. 速度滑移及其对微纳米尺度流动影响的分子动力学研究[D]. 北京: 清华大学, 2005. Cao B. Y. Molecular Dynamics Simulation of Velocity Slip and Its Effecton Micro-and Nanoscale Flow[D]. Beijing: Tsinghua University, 2005.

[29] 孟晓刚, 倪晋仁. 固液两相流中颗粒受力及其对垂直分选的影响[J]. 水利学报, 2002, 9 (9): 6-13. Meng X G, Ni J R. Analysis on forces acting on particles in solid-liquid two-phase flows and their effects on sediment vertical sorting[J]. Journal of Hydraulic Engineering, 2002, 9 (9): 6-13.

[30] 由长福, 祁海鹰, 徐旭常. Basset力研究进展与应用分析[J]. 应用力学学报, 2002, 19(2): 31-33 . You C. Progresses and applications of basset force[J]. Chinese Journal of Applied Mechanics, 2002, 19(2): 31-33.

[31] 王耀, 李宏, 郭洛方. 钢液中球状夹杂物颗粒受力情况的数值模拟[J]. 北京科技大学学报, 2013, 35(11): 1437-1442. Wang Y, Li H, Guo L F. Numerical simulation of the force condition of spherical inclusion particles in liquid steel[J]. Journal of University of Science & Technology Beijing, 2013, 35(11): 1437-1442.

[32] 王俊, 樊雪锋, 郭盛雨. 基于BBO方程研究面源红外线诱饵烟云中5 μm颗粒运动[J]. 火工品, 2011, (2): 15-18. Wang J, Fan X F, Guo S Y. Research of 5 μm Particle Movement in Surface-type IR Decoy Smoke Cloud Based on BBO-Equation[J]. Initiators & Pyrotechnics, 2011, (2): 15-18.

[33] 袁亚维, 张小兵. 高温高压多相流体动力学基础[M]. 哈尔滨: 哈尔滨工业大学出版社, 2005. Yuan Y W, Zhang X B. Foundations of Multiphase Fluid Dynamics in High Temperature and Temperature[M]. Harbin: The Press of Harbin University, 2005.

Abstract: In this paper, the movement of particles in two-phase flow under the condition of double slips was studied based on Basset-Boussinesq-Ossen equation. As to the special micro-structure on the surface of the marine-beings, the velocity distributions both in the solid-gas boundary layer and in the gas-liquid boundary layer were deduced with Karman boundary layer momentum theorem. Basset force, added mass force and drag for particles were determined through parameter method. The BBO equation was simplified and trajectory equation of particles in flow field was obtained. The slip velocity distribution was put in the particle trajectory equation and the velocity change curve under slip boundary conditions was obtained. The results indicate that the micro bubbles on the particle surface can lead slip within the boundary layer. The flow field velocity near the solid phase can be increased by micro-bubbles and the particle velocity can be increased.

Key words: particles with bubbles； solid-gas-liquid phase； boundary slip； BBO equation； movement trajectory

责任编辑 陈呈超

Characteristic Study About the Particle with Gas on the Surface in the Liquid Phase

LUAN Jian， ZHANG Ji， MEI Ning

(College of Engineering, Ocean University of China, Qingdao 266100, China)

国家自然科学基金项目(50676086)资助 Supported by National Natural Science Foundation of China(50676086)

2015-04-27；

2016-05-15

栾 健(1990-)，女，硕士。E-mail:550360699@qq.com

❋❋ 通讯作者：E-mail：nmei@ouc.edu.cn

TK121

A

1672-5174(2017)09-119-07

10.16441/j.cnki.hdxb.20150168

栾健， 张继， 梅宁. 表面驻泡颗粒在液相运动中的特征分析[J]. 中国海洋大学学报(自然科学版), 2017, 47(9): 119-125.

LUAN Jian, ZHANG Ji, MEI Ning. Characteristic study about the particle with gas on the surface in the liquid phase[J]. Periodical of Ocean University of China, 2017, 47(9): 119-125.