基于最小二乘支持向量机的无人机遥感影像分类

刘伟++赵庆展++汪传建++陈洪++李沛婷

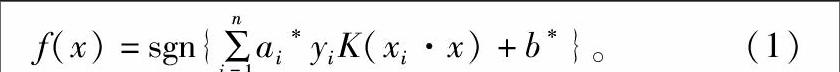
摘要：针对SVM容易出现过学习、泛化能力下降的问题，利用LSSVM在求解线性方程组时的自身优势，对高分辨率无人机多光谱影像进行地物分类识别。采用固定翼无人机搭载Micro MCA12 Snap多光谱相机，获取研究区域玛纳斯河畔的多光谱影像，首先利用最佳波段指数法与光谱信息、纹理信息结合得到最佳特征波段组合，从而降低数据维度，进而利用粒子群优化和网格搜索算法分别进行参数寻优并交叉验证方法对影像进行SVM和LSSVM对比试验。结果表明，Micro MCA12 Snap 多光谱传感器所选择的1、6、11波段组合及NDVI、NDWI、Mean特征信息组合，粒子群优化LSSVM分类的总体精度较网格搜索LSSVM高0.092%，Kappa系数高0.006；粒子群优化LSSVM分类的总体精度较粒子群优化SVM分类高2.021%，Kappa系数高0.008。试验方法改善了各种地物特别是裸地与沙石的区分，是对该相机及特征组合进行分类的有效手段。

关键词：最小二乘支持向量机；粒子群优化；网格搜索；交叉验证；无人机遥感

中图分类号： TP751；S127文献标志码： A

文章编号：1002-1302（2017）09-0187-05

随着无人机技术[1]的成熟，轻量型的多光谱传感器被广泛搭载并获取数据[2-3]，在国土资源[4-5]、环境灾害[6-7]、农情监测[8-12]等众多领域得到广泛应用。针对多波段影像数据的分类处理[13]也一直是各行业应用所面对的首要问题，已经成为研究热点之一。

支持向量机（support vector machine，SVM）是由Vapnik提出的基于统计学习理论和结构风险最小化原理的模式识别方法[14]。近年来因其具有高维空间超平面分割和局部最优解的特征，被广泛用于多光谱遥感影像的分类。陈波等基于Landsat7 ETM遥感影像构建了结合纹理的SVM分类模型并有效提高了分类精度[15]。张磊等提出一种结合改进的最佳指数法和SVM进行高光谱遥感影像分类新方法，取得比传统监督分类更高的分类精度[13]。但是标准SVM在影像分类时支持向量的数量会随着训练样本数量的增加而线性增加，从而导致分类效率降低，而且标准SVM对参数的选择依赖性大，容易出现过学习、泛化能力下降的问题。最小二乘支持向量机（least square support vector machine，LSSVM）最早由Suykens等提出[16]，是标准SVM的一种扩展，其优化问题的目标函数中利用等式约束条件代替SVM标准算法中的不等式约束条件，降低算法复杂度，提高收敛速度，使得运算时间较短。高恒振等提出一种基于波段子集最大噪声分量特征提取的LSSVM的高光谱图像分类算法并通过试验证明了算法的优越性[17]。杨佳佳等提取了遥感图像中与岩性相关的纹理、形状、光谱信息，利用LSSVM在非线性预测中的优势，对研究区地质岩性进行识别且表现良好[18]。

本试验首先结合最佳波段指数和光谱、纹理特征来确定地物分类最佳特征组合，然后利用粒子群优化[19]及网格搜索寻找最优参数并交叉验证（cross validation，CV）[20]，最后建立分类模型，将最佳波段组合作为输入变量，分别进行SVM和LSSVM分类，判断LSSVM对分类精度的影响。

1理论基础与研究思路

1.1支持向量机分类

SVM分类是一种新的机器学习方法，以结构风险最小化原则为理论基础，适当选择函数子集及该子集中的判别函数，使学习的实际风险达到最小。根据具体的分类过程寻找最优分类超平面：线性可分情况下，在原空间寻找2类样本的最优分类超平面；线性不可分的情况下，加入松弛变量进行分析，通过使用非线性映射将低维输入空间的样本映射到高维属性空间使其变为线性情况，从而使得在高维属性空间采用线性算法对样本的非线性进行分析，并在该特征空间中寻找最优分类超平面。同时由核函数（kernel function）将线性SVM推广到非线性的情况，常用核函数K（xi·x）包括线性核、多项式核、径向基核和Sigmod核，最终SVM的判别函数为：

式中：sgn{}为符号函数；ai为拉格朗日乘子；b为分类的域值；x、y为样本向量；K（xi·x）为满足Mercer条件的核函数。ai不为零的样本点就称为支持向量。a*i、b*分别表示ai、b的最优解。

1.2最小二乘支持向量机分类

虽然SVM用于图像分类有很多优点，但其求解是一个解凸二次规划问题的过程，计算过程比较复杂，当样本点较多时，时间复杂度也较高。LSSVM在其优化问题的目标函数中利用等式约束条件代替标准SVM中的不等式约束条件，最终通过求解一组线性方程得到最优解，大大降低计算复杂度，并且提高运算速度。求解最优超平面问题等价于求解如下方程：

式中：ω为权向量；b为待确定的参数；T表示矩阵的转置，在此表示为矩阵ω的转置；φ（xi）表示的是将xi从低维空间非线性映射到高维空间；γ为模型泛化能力和精度的一个折中参数且γ>0；ξ为松弛变量且ξ≥0。引入拉格朗日函数并推导可得到LSSVM的判别函数：

式中：拉格朗日乘子ai为支持向量，而K（xi·x）是满足 Mercer 条件的核函数。

1.3研究思路

高空间分辨率及光谱分辨率的遥感数据在分类时会面临大量的冗余数据，从而增加数据处理的计算复杂度及时间复杂度，因此在进行特征变量输入之前一般须对影像进行特征信息选择来降低信息维度。特征信息的选择应满足3个基本条件：波段信息量最大、波段间相关性最小、地物对所选择的波段信息具有较大的光谱差异。本试验以原始波段信息为主，结合光谱信息、纹理信息[21]对研究区域进行SVM及 LSSVM 对比分类。

根据原始波段信息的选择，本试验使用的是最佳波段指数法（optimum index factor，OIF），它是基于波段信息量标准差及波段间相关性且能反映出波段组合信息质量的方法。同时选择计算研究区对植被及水体敏感的相关指数作为光谱信息输入变量。提取纹理信息的方法很多，目前主要有基于统计方法、基于小波变换方法和基于地统计学等方法。试验先采用协方差矩阵作为变换矩阵进行主成分变换（principal component analysis，PCA）获得第一主成分后再得到影像的灰度共生矩阵（gray level co-occurrence matrix，GLCM）的相關主要参量并选择信息量最大的特征值作为纹理信息输入变量。

针对SVM和LSSVM，本试验在Matlab R2014a环境下分别以台湾大学林智仁教授设计的开源库LibSVM及LSSVM Toolbox为基础进行算法开发与验证，过程中利用群体智能优化的粒子群优化算法和网格搜索进行参数寻优并交叉验证模型参数，达到对地物进行准确划分的目的（图1）。

2研究区域及数据预处理

2.1研究区域及数据

研究区位于新疆沙湾县玛纳斯河畔，范围为86°7′58″～ 86°8′26″E，44°13′38″～ 44°14′6″N。区域内主要包含植被、水体、建筑物、裸地、沙石、阴影等地物类型。本试验使用的高分辨率遥感影像数据来自于搭载在远征-6型油动固定翼无人机上的多光谱相机Micro MCA12 Snap，该相机可同时获取12个波段（470、515、550、610、656、710、760、800、830、860、900、950 nm）的数据。其中1～5个波段位于可见光区域，波段6、7位于植被反射波谱曲线的红边区域，8～12波段位于近红外区域。波段8、5、3、1分别近似TM影像的4、3、2、1波段，可进行相关指数的计算。数据采集时间为2015年8月22日，相对航高500 m，巡航速度为130 km/h，地面采样距离GSD为22.6 cm/pixel。

2.2数据预处理

无人机影像原始数据使用Pix4D Mapper进行影像拼接。坐标系统采用WGS84，投影方式为UTM，经ENVI进行几何校正进行后续试验。

最佳波段指数选择的目的是选取像元灰度标准差高且波段间相关系数低的波段组合。计算公式为：

式中：Si为第i波段灰度值标准差；Rij为第i和第j波段间相关性系数。本试验选择3个波段组合并计算OIF值，通过 C++ 编程共产生220个波段组合，OIF值排序前10的波段组合见表1，故选择1、6、11波段作为原始波段组合。

光谱特征信息和纹理特征信息主要是通过统计方法进行选择。本试验计算了对植被及水体敏感的几种光谱指数：归一化植被指数（NDVI）、红边归一化植被指数（NDVI710）、比值植被指数（RVI）以及归一化差分水体指数（NDWI）、水波段[CM（25]指数（WBI），具体标准差计算结果依次为0.387、0.233、 0037、0.348、0.006。针对纹理特征信息，通过主成分变换和生成灰度共生矩阵方法得到主要参量：均值、方差、同源性、对比度、相异度、熵、二阶距和相关性，具体标准差统计结果依次为8.689、3.014、0.227、4.945、0.893、0.554、0.224、0.410。根据统计结果，选择NDVI、NDWI为光谱特征信息以及均值（Mean）参量为纹理特征信息。

综合以上对原始波段信息、光谱特征信息及纹理特征信息的选择，得到以波段1、6、11及特征信息NDVI、NDWI、Mean组成的最佳分类组合。图2为1、6、11（470、710、900 nm）波段的研究区域假彩色合成图。

3试验及结果分析

为获得较好的分类器，SVM与LSSVM均须要对样本及模型参数进行一定的选择。对于样本的选择，主要是选择合适分布和数量的样本点以进行模型训练及测试。试验采用径向基核函数（radial basis function，RBF）作为分类核函数。对于模型参数的选择，SVM分类时须要确定的参数有惩罚系数C和核函数参数g，而LSSVM须要确定的参数有正则化参数γ和核函数宽度δ2。采用粒子群优化算法和网格搜索方式对训练样本进行参数选择，并以多折交叉验证误差评价参数的优劣。

3.1样本选取及分类模型的建立

为保证样本的选取具有代表性，在完整研究区域内随机均[CM（25]匀采集6种地物类型（水体、沙石、裸地、植被、阴影、建筑物）的样本点，样本的可分性可用J-M（jeffries-matusita）距离及转换分离度（transformed divergence）作为评价标准。这2个度量值在0～2.0之间，大于1.9说明样本之间可分离性好，属于合格样本；小于1.8，须要重新选择样本；小于1.0，考虑将2类样本合成1类样本。对比发现，加入光谱、纹理特征信息之后J-M距离及转换分离度都达到了较高的水平，明显增加了样本的可分离性（表2）。图3为样本的N维空间可视化顯示图，可以看出选择的6类样本可以很好地分离。

粒子群优化算法是基于群体智能的新型优化算法，该算法在对鸟群行为观察的基础上，利用个体信息的共享使得整个群体在问题求解空间中产生从无序到有序的变化过程，最终得到最优解。优化参数设置为c1=2，c2=2，最大进化数为200。K-CV方法中，6个波段的样本特征子集被随机分成k个[CM（25]子集，K-CV在每个子集上进行k次验证，每次取1个子集作为测试集，其余k-1个子集作为训练集，最后将分类准确率的平均值作为样本的分类结果（本试验k取值为10）。

3.2分类结果及分析

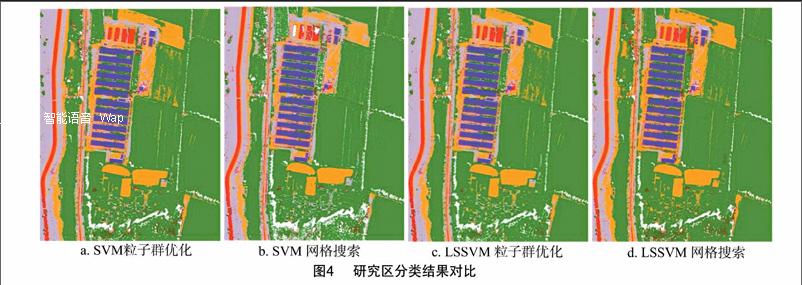
研究区域的不同分类结果如图4 所示，其中a、b分别为粒子群优化SVM分类和网格搜索SVM分类，c、d分别为粒子群优化LSSVM分类和网格搜索LSSVM分类。表3给出试验样本集各个类别的用户精度（user accuracy，UA）和生产者精度（producer accuracy，PA）。各分类方法的训练时间、测试时间、总体精度、Kappa系数如表4所示。

针对不同分类方法，结合表3、表4和图4可知沙石和裸地的生产者精度和用户精度相对较低，但对于粒子群优化过程，沙石的UA从SVM分类的89.95%上升到LSSVM分类的96.57%，PA从SVM分类的92.20%上升到LSSVM分类的97.89%，裸地表现出了同样的趋势。粒子群优化算法中，SVM、LSSVM的MSE分别为0.008 6、0.007 8，总体精度由SVM的97.833%提高到LSSVM的99.854%，Kappa系数由SVM的0.974提高到LSSVM的0.982；网格搜索过程中，SVM、LSSVM的MSE分别为0.024 6、0.012 4，总体精度由SVM的96.574%提高到LSSVM的99.762%，Kappa系数由SVM的0.969提高到LSSVM的0.976。

针对不同参数寻优方法，对比SVM及LSSVM的2种分类结果，其中，除了裸地的SVM粒子群优化后用户精度、生产者精度稍低于SVM网格搜索后的用户精度、生产者精度，植被的LSSVM粒子群优化后生产者精度稍低于LSSVM网格搜索后的生产者精度之外，其他地物的粒子群优化结果均高于网格搜索生产者精度和用户精度，甚至达到了100%。SVM分类时，网格搜索和粒子群优化的MSE分别为0.024 6、0.008 6，且粒子群优化下的训练时间、测试时间均缩短，总体精度由网格搜索的96.574%提高到粒子群优化的97.833%，Kappa系数由网格搜索的0.969提高到粒子群优化的0.974；LSSVM分类时，网格搜索和粒子群优化的MSE分别为 0.012 4、0.007 8，同样粒子群优化的训练时间、测试时间也较网格搜索短，总体精度由网格搜索的99.762%提高到粒子群优化的99.854%，Kappa系数由网格搜索的0.976提高到粒子群优化的0.982。

4结论

本试验利用无人机搭载Micro MCA12 Snap多光谱相机获得地面高分辨率多光谱影像，将最佳波段指数法与光谱信息、纹理信息结合得到最佳波段组合以降低数据维度，然后分别利用粒子群优化算法和网格搜索对最佳波段组合进行SVM和LSSVM分类并以交叉验证作为参数评价标准。试验结果显示，网格搜索最优参数时，LSSVM分类较SVM分类总体精度高3.188%，Kappa系数高0.007；粒子群优化算法参数寻优时，LSSVM分类较SVM分类总体精度高2.021%，Kappa系数高0.008；粒子群优化LSSVM分类较网格搜索LSSVM分类总体精度高0.092%，Kappa系数高0.006。试验结果表明，LSSVM对Micro MCA12 Snap多光谱影像的各分类精度均有提高，是有效的分类手段，具有一定的应用价值。

参考文献：

[1]杨进生，郭颖平，盖利亚，等. 无人直升机遥感在华北平原地裂缝监测中的应用[J]. 遥感信息，2015，30（1）：66-70.

[2]汪沛，罗锡文，周志艳，等. 基于微小型无人机的遥感信息获取关键技术综述[J]. 农业工程学报，2014，30（18）：1-12.

[3]田振坤，傅莺莺，刘素红，等. 基于无人机低空遥感的农作物快速分类方法[J]. 农业工程学报，2013，29（7）：109-116，295.

[4]张园，陶萍，梁世祥，等. 无人机遥感在森林资源调查中的应用[J]. 西南林业大学学报，2011，31（3）：49-53.

[5]王利民，刘佳，杨玲波，等. 基于无人机影像的农情遥感监测应用[J]. 农业工程学报，2013，29（18）：136-145.

[6]韩文权，任幼蓉，赵少华. 无人机遥感在应对地质灾害中的主要应用[J]. 地理空间信息，2011，9（5）：6-8，163.

[7]雷添杰，李长春，何孝莹. 无人机航空遥感系统在灾害应急救援中的应用[J]. 自然灾害学报，2011，20（1）：178-183.

[8]冯家莉，刘凯，朱远辉，等. 无人机遥感在红树林资源调查中的应用[J]. 热带地理，2015，35（1）：35-42.

[9]李冰，刘镕源，刘素红，等. 基于低空无人机遥感的冬小麦覆盖度变化监测[J]. 农业工程学报，2012，28（13）：160-165.

[10]Herwitz S R，Johnson L F，Dunagan S E，et al. Imaging from an unmanned aerial vehicle：agricultural surveillance and decision support[J]. Computers and Electronics in Agriculture，2004，44（1）：49-61.

[11]Rango A，Laliberte A，Herrick J E，et al. Unmanned aerial vehicle-based remote sensing for rangeland assessment，monitoring，and management[J]. Chinese Hydraulics & Pneumatics，2009，3（1）：11-15.

[12]Laliberte A S，Goforth M A，Steele C M，et al. Multispectral remote sensing from unmanned aircraft：image processing workflows and applications for rangeland environments[J]. Remote Sensing，2011，3（11）：2529-2551.

[13]張磊，邵振峰. 改进的OIF和SVM结合的高光谱遥感影像分类[J]. 测绘科学，2014，39（11）：114-117，66.

[14]Vapnik V N. The nature of statistical learning theory[M]. New York：Springer-Verlag，1995.

[15]陈波，张友静，陈亮. 结合纹理的SVM遥感影像分类研究[J]. 测绘工程，2007，16（5）：23-27.

[16]Suykens J A K，Vandewalle J. Least squaressupport vector machine classfiers[J]. Neural Processing Letter，1999，9：293-300.

[17]高恒振，万建伟，朱珍珍，等. 基于波段子集特征提取的最小二乘支持向量机高光谱图像分类技术[J]. 光谱学与光谱分析，2011，31（5）：1314-1317.

[18]杨佳佳，姜琦刚，陈永良，等. 基于最小二乘支持向量机和高分辨率遥感影像的大尺度区域岩性划分[J]. 中国石油大学学报（自然科学版），2012，36（1）：60-67.

[19]丁胜，袁修孝，陈黎. 粒子群优化算法用于高光谱遥感影像分类的自动波段选择[J]. 测绘学报，2010，39（3）：257-263.

[20]任哲，陈怀亮，王连喜，等. 利用交叉验证的小麦LAI反演模型研究[J]. 国土资源遥感，2015，27（4）：34-40.

[21]赵庆展，刘伟，尹小君，等. 基于无人机多光谱影像特征的最佳波段组合研究[J]. 农业机械学报，2016，47（3）：242-248，291.