用待定法解析热重曲线案例介绍
摘要:从中学化学热重曲线问题的类型入手,根据试样失重方式不同,分别利用待定化学式法和待定化学计量数法,结合具体例题探讨解题模型的应用过程及意义。指出解题模型能揭示热重曲线的反应规律,有助于学生构建结构化思维,提高化学科学素养。
关键词:待定法;热重曲线;解题模型;试题解析
文章编号:1005–6629(2017)6–0086–05 中图分类号:G633.8 文献标识码:B
中學化学热重曲线试题是近年来高考化学试题的常见题型,它是以热重法(TG)实验获得的图像数据为情境设计的试题。调研发现大多数学生畏惧此类问题,考试及作业都显示热重曲线问题是学生解答错误高发区。研究近几年的文献发现此类问题的解题策略和技巧以差量法、试误法、相对分子质量(摩尔质量)法、金属元素守恒公式法[1]、物料守恒法[2]等为主,均以个例分析见长,缺乏整体性的抽象概括,对学生思维能力要求较高,不利于学生接受。如何将这些不同的方法进行有机整合,形成解决此类问题的一般思路和方法呢?我们认为用待定法建立热重曲线的解题模型可反映其本质和规律,有助于化繁为简,抽象概括此类问题的解题思路,有助于发展学生的思维能力,提高化学科学素养。
1 热重曲线试题的类型
资料表明,中学化学热重曲线试题最早出现在2000年广东高考题中,研究近几年中、高考试题发现,这类试题大多依据结晶水合盐试样热重法实验图像而编制。一般认为加热结晶水合盐反应可视为分三步进行:第一步是脱去部分水,第二步是生成羟基盐或含水盐,第三步是生成金属氧化物;如果热重实验的气氛为空气,则加热过程中可能被氧化,反应将变得更复杂一些[3]。基于此,我们认为中学化学热重曲线试题可分为两类。第一类,试样发生分解反应,以脱水、分解等方式失重,气氛物质不参加反应;第二类,试样发生氧化、还原等反应,以氧化、还原等方式失重,气氛物质可参加反应,如氧气氧化[4]等。当然也有试题形式上是两者的结合,但本质上可以分步处理,故仍属于上述类型。
2 基于失重方式建立热重曲线解题模型
研究近十几年来热重曲线试题发现,这类问题的共同特点是:要求解答者对热重曲线进行分析判断并写出某变化的化学方程式或某温度时物质的化学式。明确考查问题以后,理顺解题思路是解决问题的关键。归纳多种解题策略和技巧,发现大多数方法基于条件逻辑分析为主,没有从热重实验原理上分析热重曲线变化的实质,所以无法抽象概括其原理,因而显得凌乱琐碎。教育解释学认为要从根本上提高学生的思维能力,就要突出程序性知识和策略性知识的地位[5]。研究表明智力模型化有比程序性知识更加灵活的应用,更能促进知识的高路迁移,帮助学生解决问题[6]。所以建立解题模型,无疑是实现低耗高效提高效率的有效途径。分析发现,热重曲线试题基于热重法实验的图像数据,有确定的化学反应发生,各固体残留物间存在某些相同的本质性的规律──失重,符合待定法的适用条件[7],这为建立其解题模型提供可能。鉴于中学生书写化学方程式需要明确各物质的化学式这一前提,针对以脱水、分解方式失重的第一类试题,原固体试样质量等于残留固体质量和失重气体质量的总和,符合质量守恒定律,用待定法设出各物质的化学式,列化学方程式通式求解;而以氧化、还原方式失重的第二类试题,由于实验气氛物质参与反应,原固体试样质量并不等于剩余固体质量和失重气体质量的总和,还有参加反应的气氛物质的质量,所以用待定法设出各物质的化学式和各物质的化学计量数,然后列化学方程式通式求解。解题模型如图1所示。即无论试样以何种方式失重,都可以通过待定法表示其化学方程式通式,然后求解。这种模型化思维方法有助于化繁为简,抽象概括此类问题的解题思路,帮助学生认清热重实验的本质规律,构建高品质思维结构。
3 热重曲线试题解题模型的应用
基于热重曲线试题的解题模型发现,热重法实验中试样的失重方式是解答此类问题的关键所在,所以分别以第一类、第二类及混合类试题为例介绍其应用过程。
3.1 固体试样以脱水、分解等方式失重──待定化学式法
例1 随着材料科学的发展,金属钒及其化合物得到了越来越广泛的应用,并被誉为“合金的维生素”。经过热重分析测得:NH4VO3在焙烧过程中,固体质量的减少值(纵坐标)随温度变化的曲线,如图2所示。则NH4VO3在分解过程中 。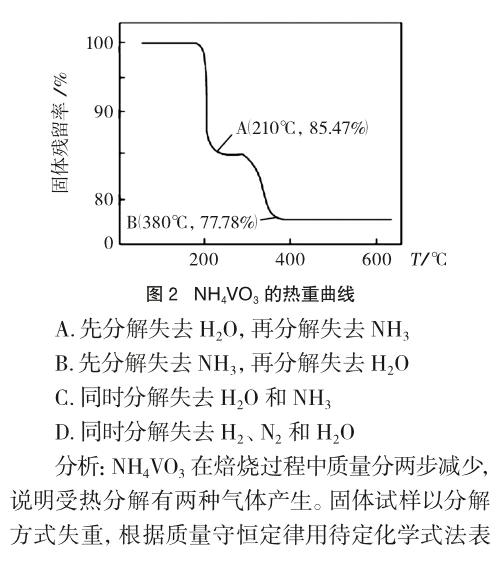

以上解题过程根据热重曲线信息,基于试样失重方式用待定法表示剩余固体物质的化学式,然后列化学方程式求解。整个解题过程思路清晰,逻辑性强,符合中学生认识化学反应的思维习惯。所以通过待定法解答以脱水、分解方式失重的热重曲线试题,能抽象概括出整个试样失重过程,使热重曲线解析有规律可循,有助于学生理解热重曲线的实质。
3.2 固体试样以氧化、还原等方式失重──待定化学式和化学计量数法
例2 正极材料为LiCoO2的锂离子电池已被广泛用作便携式电源。但钴的资源匮乏限制了其进一步发展。Co(OH)2在空气中加热时,固体残留率随温度的变化曲线,如图3所示。已知钴的氢氧化物加热至290℃时已完全脱水,则1000℃时,剩余固体的成分为 (填化学式,下同);在350~400℃范围内,剩余固体的成分为 。

分析:MnCO3在空气气氛加热过程中质量分多步逐渐减少,根据条件知MnCO3先分解成氧化物然后氧化物再转化为不同形式的氧化物。
第一步MnCO3固体试样以分解方式失重生成固体氧化物和气体化合物,设分解反应后剩余固体氧化物化学式为Mn2Ox(x为Mn的化合价),气体化合物化学式为C2O(6-x),用待定化学式法列化学方程式并将数据代入:
上例中,固体试样先后以分解、氧化两种不同的方式失重,分别根据质量守恒定律利用待定化学式、待定化学式和化学计量数法分步分类型求解,然后根据表示的化学方程式通式解答不同温度时剩余固体成分和对应化学反应的化学方程式。
总之根据失重方式建立的解题模型,能帮助学生从图像获取有效信息,从宏观实验数据抽象概括出化学符号的微观表征,能有效地帮助学生较快地解析热重曲线问题,对于培养学生化学核心素养有重要意义。
4 建立热重曲线试题解题模型的意义
通过上述例题分析发现,热重曲线试题的解题方法有一定的内在规律,其解题模型如图1所示。首先分析热重曲线试题呈现的图形、数据信息,判断所选试样以何种方式失重,如果固体试样以脱水、分解等方式失重,可通过待定法设未知物的化学式,然后列化学方程式通式求解;如果固体试样以氧化、还原等方式失重,可通过待定法设未知物的化学式和化学计量数,然后列化学方程式通式求解。如果试样先后以两种不同的方式失重,可分步运用上述方法解答。总之运用待定法建立热重曲线解题模型符合中学化学计算的一般解题步骤,即先待定化学式和化学计量数再代入计算,与教材中例题解题顺序不同,考查学生的逆向思维能力,符合科学探究要求中的假设-验证思维模式。该解题模型基于化学科学观念──质量守恒定律和化学方程式计算,对复杂的热重曲线问题抽象概括出一般解题模型,有广泛的适应性和严密的逻辑性,有利于学生快速抓住问题的核心形成有效的思路,有利于学生建构清晰的思维结构从而高效地解答。而差量法、相对分子质量法要求学生对物质的化学式较熟悉,而大多数中学生对陌生的中间产物往往很难快速作出判断;试误法缺乏目标需要多次试验;公式法本质上基于金属元素守恒不考虑反应过程,计算简洁明了,但是要求学生强化记忆公式,很难培养学生的思维能力;物料守恒法以确定某温度时物质中各元素原子个数比为突破口,能快速确定固体的成分,但对于多种成分同时失重或者确定失重的化学方程式有一定的局限。当然利用待定法确定的解题模型计算量较大,对学生有一定计算能力要求,但是相对其他解法对思维能力的要求低,具有学科通识性,易于学生接受,特别是解答复杂的多步失重问题更有优势,更能体现实验背后所蕴涵的化学学科本质和规律,有利于引导学生关注学科方法和建构学科观念。
参考文献:
[1][5]韩江涛,杨云.中学化学热重曲线类试题文献分析及建议[J].化学教学,2016,(7):82~86.
[2]霍本斌.利用物料守恒巧解热重曲线类习题[J].化学教学,2016,(10):69~73.
[3]李稳.一些无机水合盐的热分解动力学研究[D].南京:南京理工大学硕士学位论文,2012:810.
[4]杨永喜,蒋军成,趙声萍等.硫化亚铁氧化热重实验及动力学分析[J].工业安全与环保:2010,(12):57.
[6]黄梅,黄希庭.知识的加工阶段与教学条件[J].教育研究:2015,(7):108~115.
[7]百度百科待定系数法http://baike.baidu.com/view/ 161511.htm.2016-12-6.

