独立光伏系统中考虑小型压缩空气储能的容量配置
杨 安,杨江涛,刘 佳,刘俊恒,刘 天
(1.国网湖南省电力公司 岳阳供电分公司, 湖南 岳阳 414000; 2.国网湖南省电力公司 检修公司, 湖南 长沙 410000;3.智能电网运行与控制湖南省重点实验室(长沙理工大学), 湖南 长沙 410004)
独立光伏系统中考虑小型压缩空气储能的容量配置
杨 安1,杨江涛2,刘 佳3,刘俊恒1,刘 天1
(1.国网湖南省电力公司 岳阳供电分公司, 湖南 岳阳 414000; 2.国网湖南省电力公司 检修公司, 湖南 长沙 410000;3.智能电网运行与控制湖南省重点实验室(长沙理工大学), 湖南 长沙 410004)
小型压缩空气储能是一种新型的储能方式,可与光伏配合组成独立光伏系统,基于用户对供电可靠性和经济性的双重需求,合理配置储能和光伏系统的容量,可促进储能和光伏产业的共同发展。在考虑负荷缺电率和能量溢出率2个指标的基础上,计及装置设备的初始投资成本、运行维护成本、残值和各部分收益,建立系统经济性模型,以年费用最低为目标,配置最优的光伏容量和小型压缩空气储能容量。结果表明,综合考虑负荷缺电率和能量溢出率,合理配置容量,可以保证系统供电可靠性和经济性。
小型压缩空气储能;光伏发电;容量配置;经济性分析
0 引言
化石能源供应的紧缺以及环境污染的加重,使光伏发电的优势越发突出。而光伏发电的间歇性和不稳定性,需要引入储能来解决。液气压缩空气储能作为小型压缩空气储能的一种,是一种新型的电力存储形式,利用液体压缩空气,减少了气体泄露,且零污染[1-2],采用压力容器存储,不依赖地下溶洞,使用区域更广泛随意,建造规模根据实际情况可大可小,无需建立大型电站,能直接和光伏发电或风能发电等新能源配套使用,建造容易。在远离大电网的偏远山区、海岛或者牧场、边防哨所等地,环境特殊人烟稀少,电力需求量较少,但由于地形、交通等限制,燃料运输和线路架设困难,使电能供应成为难题。引入光伏发电即可从根本上解决其供电困难问题,当其与小型压缩空气储能装置相互配合构成独立系统,不但弥补了光伏发电夜间无出力的局限性,更确保了该区域的供电可靠性,没有环境污染,势必具备很好的发展前景。
目前储能的初始投资成本较贵,短时期内系统的单位建造成本改变不大,储能的容量配置太小,对拟改善的问题效果不明显,太大又会造成不必要的投资冗余,影响经济性。在独立光伏系统中,容量配置和经济性结合在一起,常把函数目标定为系统成本最小,把约束条件定为供电可靠性等进行优化配置[3-4]。文献[5]在储能的配置中考虑了电池储能的特殊性,寿命跟放电深度密切相关,采用雨流计算法量化使用寿命,再以年均成本最小为目标函数优化。但是这些都只单纯考虑配置储能的容量[6],较少考虑光伏、储能和负荷的配合关系。
本文以年费用最小为目标,考虑光伏和储能系统以及和负荷三者间的能量交换,并且兼顾影响系统供电可靠性的负荷缺电率和能量溢出率指标,配置系统容量,讨论系统经济性。
1 模型分析
1.1 带储能的独立光伏系统结构及功能
基于小型压缩空气储能的独立光伏发电系统结构简图如图1所示,由光伏阵列、最大功率点跟踪装置(MPPT)、双向控制器、压缩空气储能装置、逆变器、交流负载和直流负载组成。
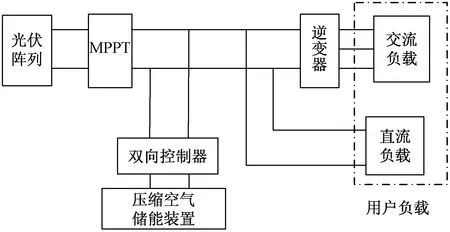
图1 带储能的独立光伏系统结构图
由于用户负荷并不遵循 “日出而作,日落而熄”,会出现白天有电剩余,晚上缺少电量的情况,采用小型压缩空气储能装置作为电能的存储单元,可实现电量在光伏发电和用户使用电量间的调度。并且可以提高系统的供电可靠性,确保重要负荷的用电需求。
1.2 光伏系统数学模型
可用标准测试环境下的测量数据为标准来计算其他非标准运行工况下光伏的出力,PV的功率输出模型[7]如下:

(1)
其中,光伏组件的实际温度测量较困难,可通过测试环境温度,由经验公式估算得出光伏组件温度:
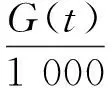
(2)
式中:Ppv(t)为t时刻光伏输出实际功率;PSTC表示标准环境下输出的额定功率,kW;G(t)为t时刻太阳辐照度,W/m2;GSTC为标准测试条件下的太阳辐照度,1 000 W/m2;k表示功率温度修正系数,-0.004 7/℃;TC(t)为t时刻组件实际的温度,℃;TE(t)为t时刻环境温度;TSTC为标准环境下的参考温度,25 ℃。
1.3 小型压缩空气储能数学模型
区别蓄电池等常规储能方式,小型CAES有一大优势就是CAES没有自放电[8]。可用荷电状态Soc衡量储能装置的实时储存电量情况,式(3)和(4)分别表示充电和放电状况下前后时刻的荷电状态递推关系。

(3)

(4)
式中:Soc(t)表示第t时段结束时储能剩余电量,它与(t-1)时刻的荷电状态以及t时段的充放电功率有关。Soc(t-1)表示第(t-1)时段结束时储能剩余电量;η表示储能的充放电效率;Pyq(t)表示t时段充放电功率;Δt表示仿真t时段大小;Wyq.max表示储能额定容量。
2 系统可靠性指标
2.1 负荷缺电率
在确定的负载水平下,在光伏系统中引入储能,可以提高系统供电可靠性。但是在一定负载条件下,如果供电可靠性过高,需要光伏容量和配置的储能容量会很大,相应的投资也将增大,会越不经济。供电可靠性过低,所对应的缺电或停电势必影响生产生活,造成经济损失甚至社会损失。所以,在确保系统的经济性的同时必须设置一定的可靠性系数。
当供电可靠性系数λ=1时,系统的功率满足:
Ppv(t)+ηPyq(t)=Pload(t)
(5)
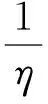
(6)
其中,式(5)表示储能放电时,光伏和储能共同给用户供电的功率平衡情况;式(6)表示储能充电时,光伏发电给用户供电,多余的电量给储能充电的功率平衡情况。
储能装置的实时容量递推关系如下所示:
Wyq(t+1)=Wyq(t)-
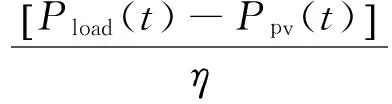
(7)
Wyq(t+1)=Wyq(t)+
(8)
其中,式(7)表示储能放电时的容量递推关系;式(8)表示储能充电时的容量递推关系。
在光伏发电量小于负荷所需电量时,由光伏和储能联合给用户供电,如果当储能装置的荷电状态已达到最小的极限Socmin,都小于用户所需的电量,即:
Wyq(t+1)=Wyq.min(t)
(9)
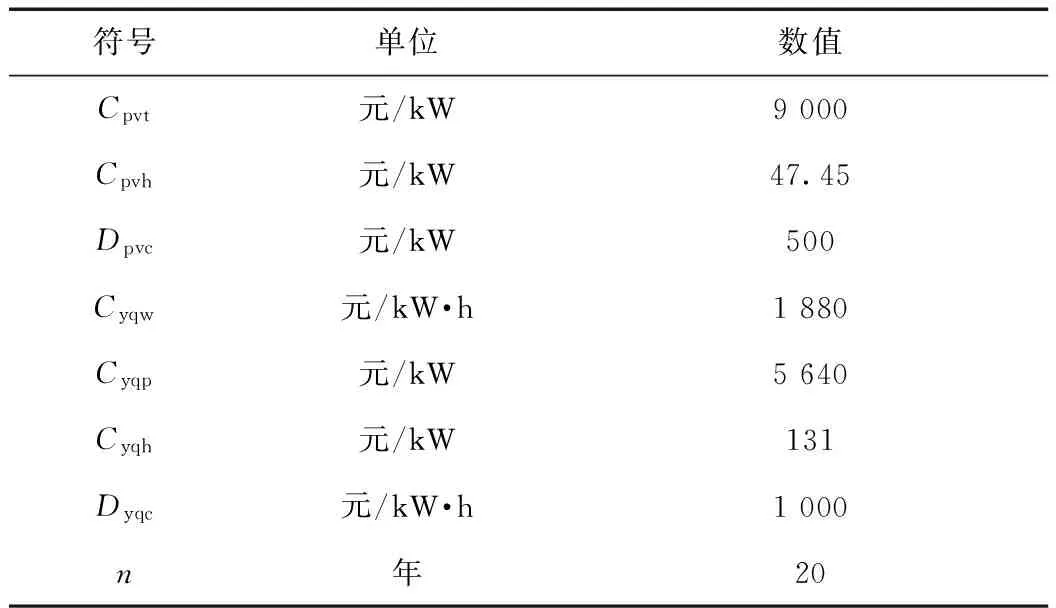
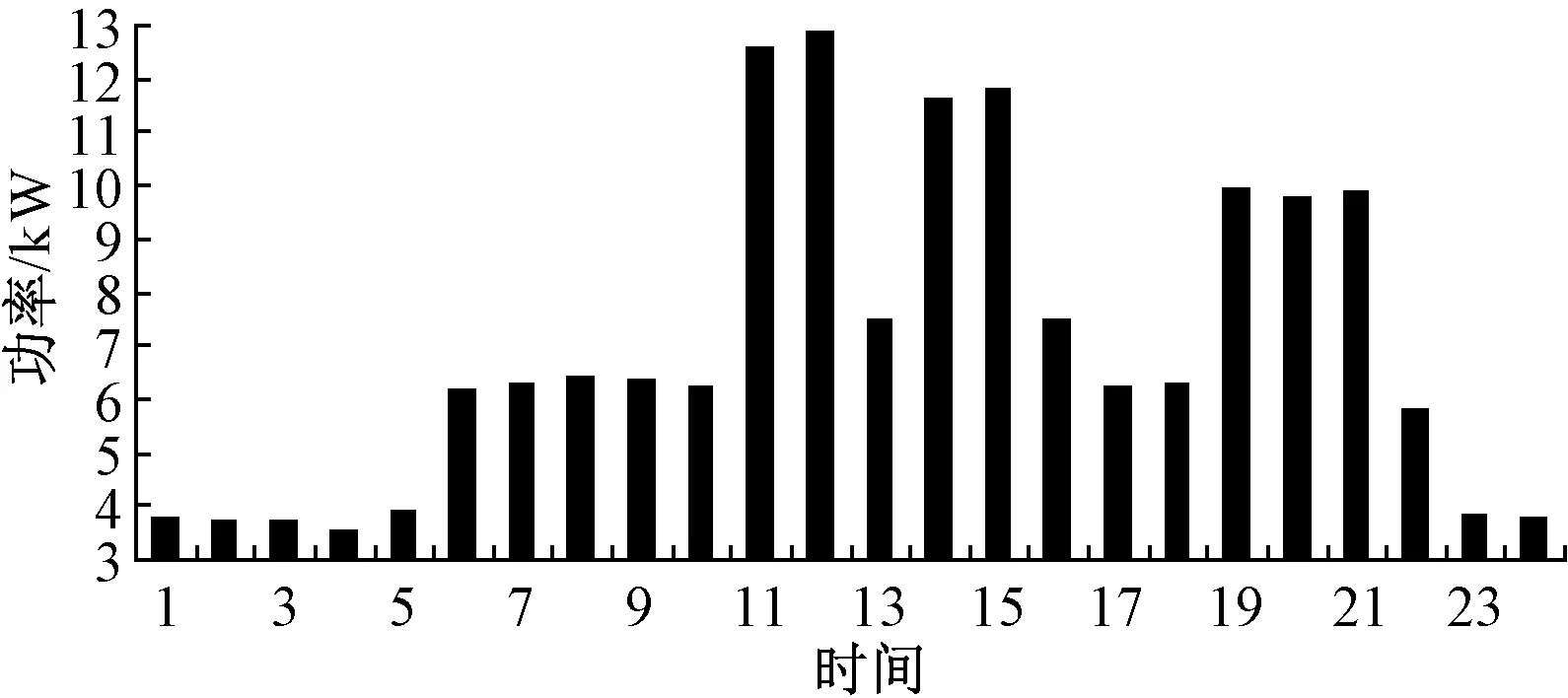
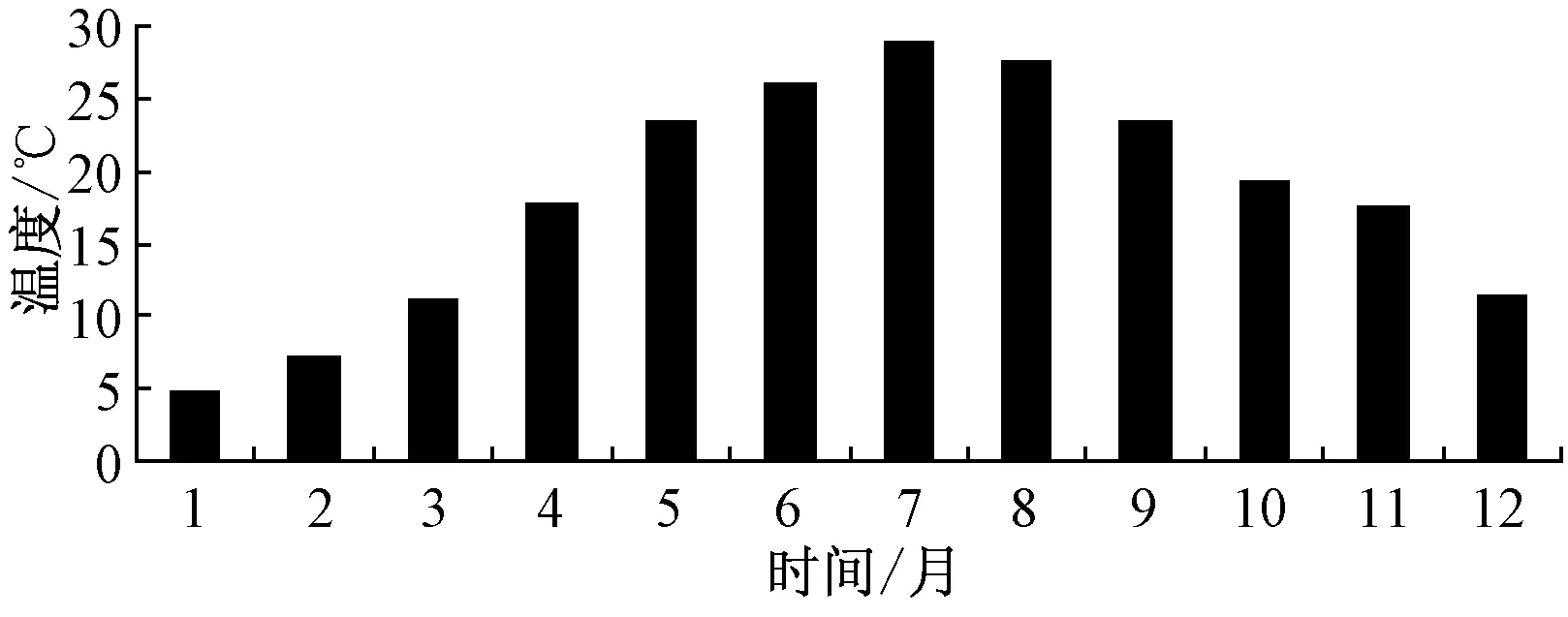
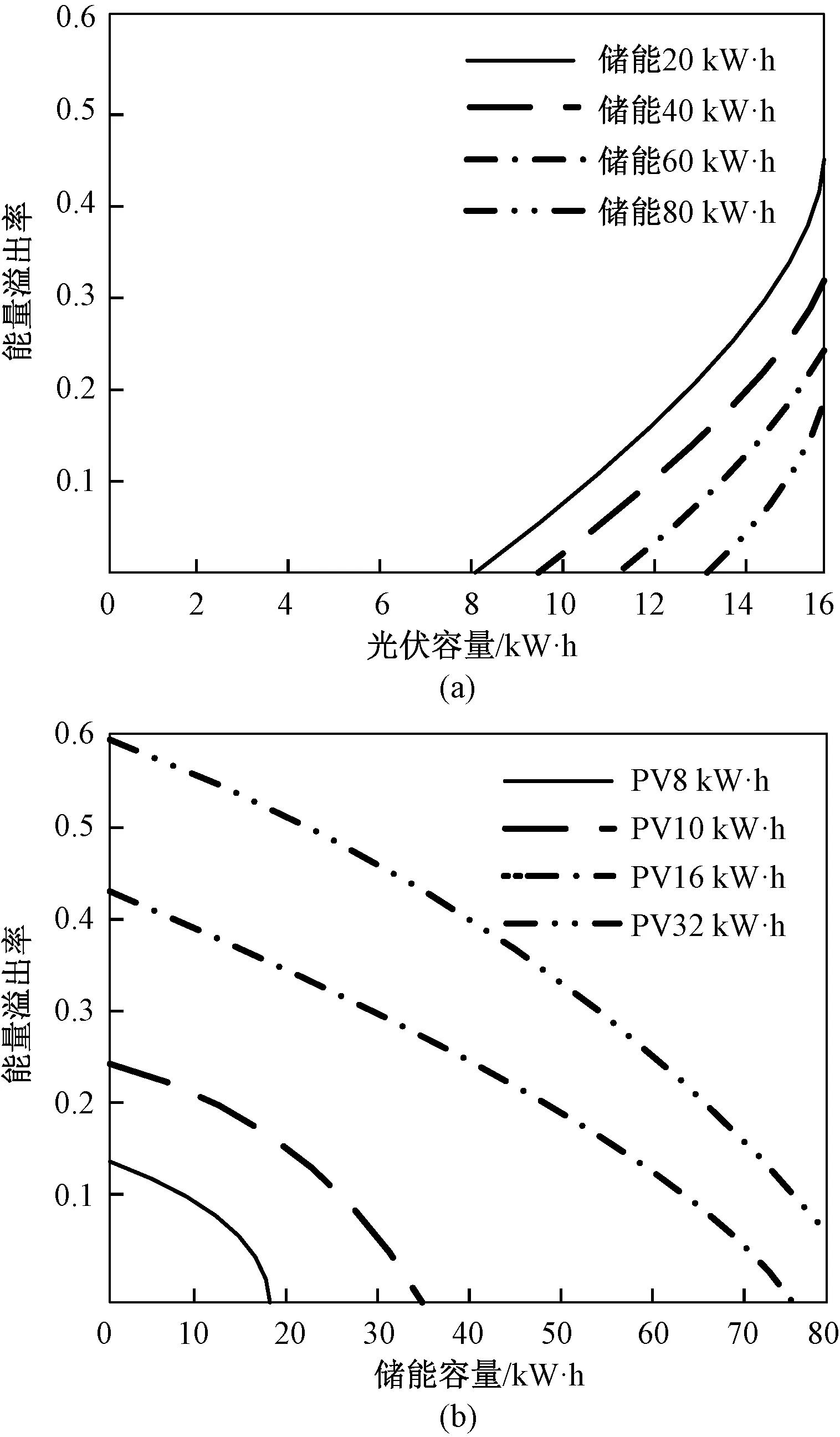
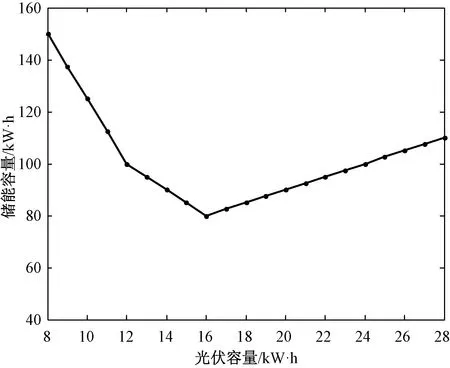
Ppv(t)+ηPyq(t) (10) 这时就会出现供电不足,则需要切除一部分负荷,以保证重要负荷的正常运行。负荷缺电率λq定义为负荷缺少的电量与负荷总需求电量的比值[9],可表示为: (11) 负荷缺电率反映着供电可靠性,λq的值在[0,1]间,当λq取值为0时,供电可靠性最高,可需要配置很大的储能系统才能满足要求,势必对经济性产生负面影响;当λq取值为1时,供电可靠性最差,用户的正常用电生活都会受到影响。 2.2 能量溢出率 当光伏发电量大于负荷所需电量,多余的电量给储能充电,若储能装置完全充满,荷电状态Soc达到最大的极限Socmax,还有多余的电量,即: Wyq(t+1)=Wyq.max(t) (12) (13) 这时就会出现有电量剩余,能量溢出,需要对光伏电池进行弃光处理减少系统发电出力。能量溢出率λy定义为系统溢出的能量与光伏总发电量的比值,可表示为: (14) 能量溢出率在工程上常被用来权衡可再生能源发电系统的规模大小,取值在0.05~0.3间,当λy取值为0时,表示系统所发的正好被负荷全部使用,没有能量溢出,λy越大,说明系统中光伏发电量溢出的越多被利用的电能越少,会造成很大的浪费。 本文中整个带小型压缩空气储能的光伏系统的所有者是用户。对用户来说系统要能满足供电可靠性,使基本生产生活受到保障,并且能带来一定收益。所以从用户的角度来研究系统的成本和收益,并且考虑可靠性,来配置系统容量。 3.1 系统收益模型 系统的年收益由发电补贴收益、电费收益,以及光伏组件和储能装置的残值收入组成。整个系统年收益表示为: IySum=Ib+Id+Ipvc+Iyqc (15) (1)发电补贴效益 由于光伏发电与传统能源发电相比不存在经济优势,根据国家政策规定,对光伏发电可以提供一定补贴,以促进光伏的发展进程,所以年发电补贴效益可表示为: (16) 式中:Cbt为补贴电价,元/(kW·h)。 (2)电费效益 安装独立系统的地区一般是无法从电网购电的地区,电费效益表现为在节省电费上的盈利,一年产生的电费效益有2部分:一部分是光伏电池发电用户直接使用;另一部分为光伏电池产生的多余电量经储能装置储存之后再在缺电的情况下放出供电使用。年电费效益表示为用户年用电量与当地分时电价的乘积: (17) 式中:C0表示电价,元/(kW·h);Pload(t)表示t时段的用户负荷用电量。 (3)光伏组件年等值报废残值 在项目使用年限结束之后,光伏还具有一定的残值价值,可折算成年等值报废残值: (18) 式中:Ipvc表示光伏年等值报废残值,元;Dpvc表示光伏组件单位容量的残值,元/kW;n表示项目使用寿命,年。 (4)储能装置年等值报废残值 储能装置使用寿命结束时,剩下的金属材料等都具有回收利用价值,换算为年等值形式表示为: (19) 式中:Iyqc表示储能装置年等值报废残值,元;Dyqc表示单位容量的储能装置残值,元/kW·h。 3.2 系统成本模型 整个独立光伏发电系统的总成本费用包括光伏发电的初始投资成本和运行维护成本,以及小型CAES装置的初始投资成本和运行维护成本。一般工程使用年限为20 n,光伏发电使用寿命25年左右,小型CAES的使用寿命在30 n以上,所以在工程的运行年限内均不需要考虑更新置换成本。 (1)系统初始投资成本 系统的初始投资成本包括光伏和小型CAES装置的初始投资成本,光伏的投资成本与功率有关,而小型CAES的投资成本与功率和容量都有关。 Mt=CpvtPpv+CyqwWyq.max+CyqpPyq.max (20) 式中:Mt表示系统初始投资成本,元;Cpvt表示单位装机容量成本,元/kW;Ppv表示光伏装机功率,kW;Cyqw表示储能单位能量成本,元/kW·h;Cyqp表示储能单位功率成本,元/kW;Pyq.max表示储能额定功率,kW。 由于,初始投资成本为一次性投入,考虑资金的时间价值,可以用年等值投资成本表示: Mtn=Mtf (21) (22) 式中:Mtn表示系统年等值投资成本,元;f表示年资金回收率;r表示折现率。 (2)系统年运行维护成本 在设备使用过程中,需要定期维修保养,支付工人的工资等,年运行维护成本可表示为: Mh=CpvhPpv+CyqhPyq.max (23) 式中:Cpvh为光伏年单位运行维护成本,元/kW;Cyqh为单位储能的年运行维护成本,元/kW。 综上所述,系统年总成本费用为: MySum=Mtn+Mh (24) 3.3 目标函数及约束条件 根据系统的成本和各项收益,建立以系统年费用最小的目标函数: minF=MySum-IySum (25) 考虑系统的经济性和可靠性,得到系统容量配置的约束条件: -Pyqmax (26) 0≤Wyq(t)≤Wyq.max (27) Socmin≤Soc≤Socmax (28) 0≤Ppv(t)≤Ppv.max (29) λq≤λq.max (30) λy≤λy.max (31) 式(26)、(27)、(28)是储能装置电量约束、容量约束、功率约束条件。式(29)为光伏发电的功率约束条件,式(30)、(31)为系统可靠性约束。 4.1 基础数据 以华中地区(东经134°,北纬30°)的相关统计数据[10]为例,根据该地区的年辐照度、温度和负荷需求情况,采用本文提出的模型进行容量配置,并进行相关的经济性分析。表1是单位容量光伏和储能装置的相关费用及运行数据,图2为该地月平均温度曲线,图3为该地区年辐照度曲线,图4为典型用户日负荷功率需求情况。假设该地的电价为C0=0.682元/kW·h,小型CAES装置的初始Soc=0.5,变化范围为0.1~0.9。政府补贴电价为Cbt=0.42元/kW·h,折现率r=0.05,负荷缺电率λq·max=0.1,能量溢出率λy·max=0.2。 表1 单位容量光伏和小型压缩空气储能装置的相关费用及运行数据 图2 月平均温度曲线 图3 年辐照度曲线 图4 典型日负荷功率需求情况 4.2 仿真结果与分析 由于在每天光伏发电工作时段内温度差较小,可采用该月的平均温度代替该月每天的温度。为简单起见,假设全年每天的负荷需求情况相同,以某一典型日负荷需求情况来模拟。根据建立的数学模型和经济性模型,在确定的负载条件下,考虑负荷缺电率和能量溢出率,来配置最优的储能容量和光伏容量,使系统的经济性最优。 图5为负荷缺电率与光伏容量和储能容量的关系图。 图5 负荷缺电率与储能容量和光伏容量的关系 由图5可看出:(1)图5(a)在确定的负载需求和储能容量下,增大光伏容量可以提高供电可靠性。如在储能容量为20 kW·h时,增大光伏容量到16 kW时,负荷缺电率从0.5降到了0.38,即供电可靠性从0.5提高到了0.62;(2)图5(b)中在确定的负载需求和光伏容量下,增大储能容量可以减小负荷缺电率。如在光伏容量为8 kW时,增大储能容量到80 kW·h时,负荷缺电率从0.6降到了0.22;(3)对比图5(a)和图5(b)看出,在确定的负载需求下,系统中的光伏容量增大,所需配置的储能容量可减小,而对应的供电可靠性也越高。反之,配置的储能容量越大,所需光伏容量越小,对应的供电可靠性也越高。图5(b)中曲线的变化率明显大于图5(a)的曲线变化率,表明增大储能容量对减小负荷缺电率增大供电可靠性的作用明显优于增大光伏的容量。 图6表示的是供电可靠性和系统成本的关系。由图可见,负荷缺电率越小,供电可靠性越高,系统成本投入越高,并且在负荷缺电率0~0.1范围内,成本变化速度很快,说明在缺电率为0.1时,如果要再减小负荷缺电率,将要投入很大的成本作为代价。所以为保证用户的供电可靠性和系统的经济性,需要允许一定的负荷缺电率。 图6 负荷缺电率与系统成本的关系 图7是能量溢出率与光伏容量和储能容量的关系。 图7 能量溢出率与储能容量和光伏容量的关系 由图7可得出:(1)图7(a)中在一定的负载条件下,光伏容量很小时,负荷所需的功率大于光伏发电功率,没有多余的能量溢出。储能的规模越大,开始有能量溢出时的光伏容量也越大,在相同的光伏规模下,储能容量越大溢出的电能越少,且随光伏规模越大,同一能量溢出率所对应的储能容量越大。说明储能能够储存多余的光伏发电量,减少电能的溢出。(2)图7(b)中在一定的负载条件下,储能容量相同时,光伏容量越大,能量溢出率越大,例如在10 kW·h时,光伏容量分别为8 kW、10 kW、16 kW、32 kW时,能量溢出率分别为0.17、0.22、0.4、0.55。储能的容量越大能够存储的电量也越多。 由以上分析可见,λq和λy与光伏容量、储能容量有着耦合关系。在光伏容量很小时,能量溢出率小,但是负荷缺电率大,不能满足用户的用电需求。在满足供电可靠性下,光伏容量越大,负荷缺电率越小,但能量溢出率增大。为此,可以增大配置储能容量来储存多余的光伏发电量,减少能量的溢出,且储能的容量越大,作用越明显。但是储能容量配置越大,系统所需的成本越大。所以为了系统的经济性和供电可靠性要合理考虑负荷缺电率和能量溢出率2个指标,合理的配置光伏容量和储能容量。 在算例给定的负荷缺电率λq.max=0.1,能量溢出率λy.max=0.2的情况下,可得到符合的光伏容量和储能容量关系如图8所示。 图8 光伏容量和储能容量关系 以年费用最小为目标函数,在图中可寻找到最优的光伏装机功率和储能容量。得到光伏装机功率和储能配置容量的最佳组合是16 kW和80 kW·h,储能的额定功率为12 kW。年最小费用为-35 618元。各项成本和收益见表2。从表2中可看出,每年光伏系统的投资者支付系统的等值投资成本为29 690元,运行维护成本为2 332元,共计32 022元。在获得每年的光伏发电补贴效益,电费效益和残值收入之后,每年实际支出的成本为-35 618元,即每年可收入35 618元,可知系统是盈利的。在系统的整个运行期20 n内,投资者可获得总收益为71.2万元。 表2 系统各部分成本和收益 元 用小型压缩空气储能和光伏发电组成独立光伏发电系统能解决偏远地区的用电难题,并且无环境污染。负荷缺电率和能量溢出率影响着供电可靠性、容量配置和系统经济性。本文在考虑负荷缺电率和能量溢出率指标的基础上,以年费用最低为目标,配置最优的光伏容量和储能容量。结果表明,综合考虑负荷缺电率和能量溢出率指标,配置最合理的容量,系统能给用户解决用电难题并且带来经济效益。 [1] 黄先进,郝瑞祥,张立伟,等.压缩空气与超级电容混合储能系统能量控制策略[J].北京交通大学学报,2014,38(4):56-62. [2] 黄先进,郝瑞祥,张立伟,等.超级电容压缩空气混合储能应用于光伏发电系统的EMR建模与控制[J].高压电器,2015,51(6):53-61. [3] 吴小刚,刘宗歧,田立亭,等.独立光伏系统光储容量优化配置方法[J].电网技术,2014,38(5):1271-1276. [4] 杨珺,张建成,周扬,等.针对独立风光发电中混合储能容量优化配置研究[J].电力系统保护与控制,2013,41(4):38-44. [5] 韩晓娟,程成,籍天明,等.计及电池使用寿命的混合储能系统容量优化模型[J].中国电机工程学报,2013,33(34):91-97. [6] FATEMEH J A, GHOLAMHOSSEIN R, MEHRDAD A.Design of an optimum hybrid renewable energy system considering reliability indices[C].Electrical Engineering (ICEE) 2010 18th Iranian Conference on, 2010: 842-847. [7] 丁明,王波,赵波,等.独立风光柴储微网系统容量优化配置[J].电网技术,2013,37(3):575-581. [8] 杨安,孙春顺,杨江涛,等.液气压缩空气储能在光伏发电中的经济性分析[J].电力科学与工程,2015,31(6):37-42. [9] JOSKO P.Modeling of hydro-pneumatic energy storage system[C].2013 8th EUR- OSIM Congress on Modelling and Simulation, 2013: 124-129. [10] 胡国珍,段善旭,蔡涛,等.基于液流电池储能的光伏系统容量配置及成本分析[J].电工技术学报,2012,27(5):260-267. Capacity Configurations of Stand-alone Photovoltaic System Based on Small Scale Compressed Air Energy Storage YANG An1, YANG Jiangtao2, LIU Jia3, LIU Junheng1, LIU Tian1 (1.State Grid Hunan Electric Power Company Yueyang Power Supply Company,Yueyang 414000,China;2.State Grid Hunan Electric Power Company Maintenance Company, Changsha 410000,China; 3.Changsha University of Science and Technology Hunan Province Key Laboratory of Smart Grids Operation and Control, Changsha 410004,China) As a new energy power generation, the small scale compressed air energy storage works in with photovoltaic energy to constitute a stand-alone photovoltaic system, and the economy as well as the reliability are considered to deploy the energy storage and system capacity.Take two important indexes into account, namely the load power shortage rate and energy overflow rate, and an economic model is established with the costs and benefits included, such as the initial investment in equipment, operation and maintenance cost, salvage value and part of the proceeds.Aiming at minimizing the annual cost, the optimal PV capacity and energy storage is calculated.The results show that considering the load power shortage rate and energy overflow rate, the rational allocation of capacity can guarantee the reliability and economical efficiency of power supply system. small scale compressed air energy storage; photovoltaic generation; capacity configurations; economy analysis 10.3969/j.ISSN.1672-0792.2017.06.003 2017-01-12。 TM919 A 1672-0792(2017)06-0012-07 杨安(1990-),女,工程师,研究方向为电力系统运行与控制,压缩空气储能的研究与运用。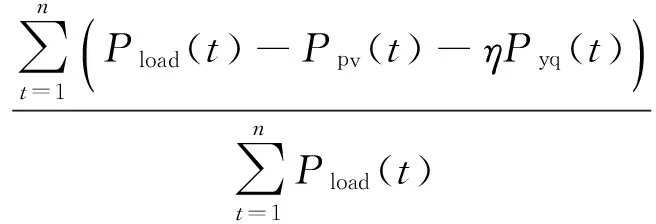
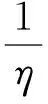

3 系统容量配置模型


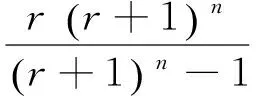
4 算例分析




5 结论

