基于基阵特性提高声发射频次的方法研究

王 晨， 郭英歌， 王润田

(中国科学院 声学研究所东海研究站， 上海 201815)

基于基阵特性提高声发射频次的方法研究

王 晨， 郭英歌， 王润田

(中国科学院 声学研究所东海研究站， 上海 201815)

针对传统的多波束探测效率低等问题， 提出了一种利用栅瓣来提高声发射频次的方法. 在设计发射波束形成的基阵时， 为了防止由于阵元间距过大产生栅瓣， 通常采用密排阵的方式来规避栅瓣现象， 但这样又会增加发射机的复杂程度. 然而， 栅瓣的存在也有其本身可以利用的价值. 本文利用MATLAB对发射波束形成的方向图进行了仿真分析， 总结了在不同基阵条件下主瓣和栅瓣的变化规律. 介绍了利用线列阵同时向两个不同方向发射波束的方法， 并利用加权法对阵列特性进行了优化.

发射波束形成； 阵元间距； 栅瓣； 多波束； Chebyshev加权

0 引 言

声纳是获取海底信息的主要手段之一， 无论是侧扫声纳还是多波束声纳， 都已在获取海底信息方面得到了普遍应用. 波束形成技术作为声纳系统的重要组成部分， 具有运用简单， 性能稳定等优点[1-2]. 通常所说的波束形成技术是指针对某一方向的信号， 补偿由于阵元空间位置不同引起的相位差， 同相叠加后， 实现指定方向上能量的最大化[3-5]. 也就是所谓的接收波束形成技术. 接收波束形成能抑制其他方向的干扰， 实现定向接收. 但有时为了实现声波能量的定向传输， 往往需要采用发射波束形成技术， 尤其是在参量阵声呐技术应用中. 发射波束形成是将发射能量集中在某一方向上， 实现用较小的发射功率获得更大的声源级和更窄的发射波束.

传统的发射多波束是采用旋转单波束的方式， 即从观察扇面的左(右)极限开始发射一个波束， 接收回波后旋转一定角度再发下一个波束， 直至完成整个扇面的扫描[6]. 随着海洋事业的急速发展， 这样的扫描速率， 俨然无法满足如今的探测需求.

在相控阵声纳的发射波束形成过程中， 当线列阵的阵元间距较大时， 在形成的波束图中除了主瓣之外还会有其它极大值出现， 即栅瓣. 在传统应用中， 栅瓣的出现无疑是对主瓣的干扰， 是需要控制基阵参数努力规避的. 但是， 在总结栅瓣的变化规律时发现， 栅瓣主要与阵元间距和主瓣方向角有关. 阵元间距越大， 栅瓣越容易出现. 随着主瓣方向角的偏转， 栅瓣方向角也发生偏转， 并且波束宽度逐渐变窄， 幅值也逐渐增加. 尤其是当阵元间距大于一个信号波长时， 栅瓣和主瓣在某些方向有近似相同的波束宽度和幅值. 栅瓣现象的产生， 表明一个发射线列阵可以实现同时向两个方向发射特性相同的波束. 这样就可以用来弥补传统回声声纳只能发射单波束， 探测效率低的缺陷. 利用相控阵的这个特性， 可以用来适当改善多波束参量阵声纳的工作效率. 相对于相控阵ADCP采用波束形成的方法分别形成4个发射波束而言[7]， 同样可以利用栅瓣现象同时在两个正交方向上同时发射两列波， 提高工作效率.

1 发射波束形成的基本原理

波束形成是指将以一定几何形状(直线、 圆柱等)排列的多元基阵各阵元输出经过处理(例如加权、 延时、 求和等)形成空间指向性的方法[8]. 波束形成技术正在快速发展， 方法种类也越来越多， 最常用最基本的方法就是时延或相移方法.

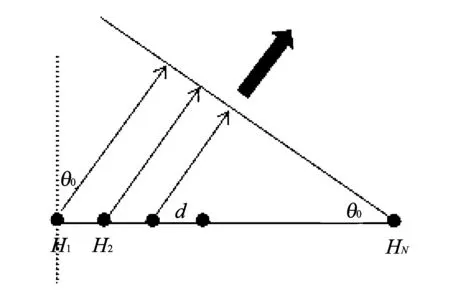
图 1 发射波束形成Fig.1 Transmit beam-forming

对于一个等间隔N元线列阵， 发射波束形成就是对线列阵的各个阵元在发射信号时加以延时. 假设阵元间距为d， 声速为c， 信号频率为f， 发射波束方向角为θ0(设基阵的法线方向为0°， 法线右侧的波束方向角为正， 左侧为负). 如图 1 所示.

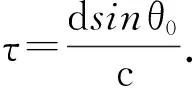
选取阵元H1为时间参考点， 假设H1输出的单频信号为

F1=Acos(ωt).

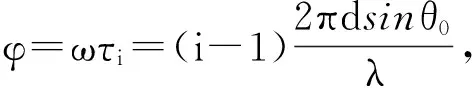
信号叠加

(N-1)ω τ/2].

归一化后得到线列阵在θ0方向的指向性函数[9]

式(4)是假设阵元为点源时的指向性函数. 在实际情况中， 阵元是有尺寸的， 且对阵列指向性函数有影响[10-12]. 圆形活塞式换能器是搭建基阵最常用的基元， 假设其振动面的半径为R， 则根据乘积定理可知， 基元非点源时的阵列指向性函数为

2 线列阵同时向两个不同方向发射波束的方法

2.1 方法介绍

当阵元间距d大于半波长时， 发射基阵除了形成主瓣外还可能会出现栅瓣. 这一现象通过指向性函数的理论推导也可以得出.

当函数表达式中πd(sinθ-sinθ0)/λ=mπ,m=0,±1,±2,…时，D(θ)=1. 讨论m的两种情况：

1) 当m=0时，θ=θ0， 出现的最大波瓣即为主瓣；

2) 当m≠0时， 出现的最大波瓣即为栅瓣， 其位置可以表示为

取阵元数N=32， 信号频率f=20 kHz， 阵元间距d=3/4λ， 阵元尺寸a=50 mm， 发射波束指向角分别为θ0=10°, 30°， 得到仿真结果如图 2 所示.

假设法线右侧方向角为正， 左侧为负. 可见， 随着方向角的增大， 在负方向上出现了栅瓣. 当θ0=10°时， 未出现栅瓣； 当θ0=30°时， 栅瓣方向角θm≈56°， 与理论计算值相同.

仿真过程中发现， 栅瓣随着主瓣的偏转而逐渐发生变化. 主瓣的偏转角越大， 栅瓣的宽度越窄， 幅值越高. 为了使得栅瓣与主瓣有相同的指向特性， 选取阵元间距d=1.3λ， 阵元数N=32， 信号频率f=20 kHz， 阵元尺寸a=50 mm， 主瓣方向角分别取θ0=15°,20°,25°,30°， 如图 3 所示.

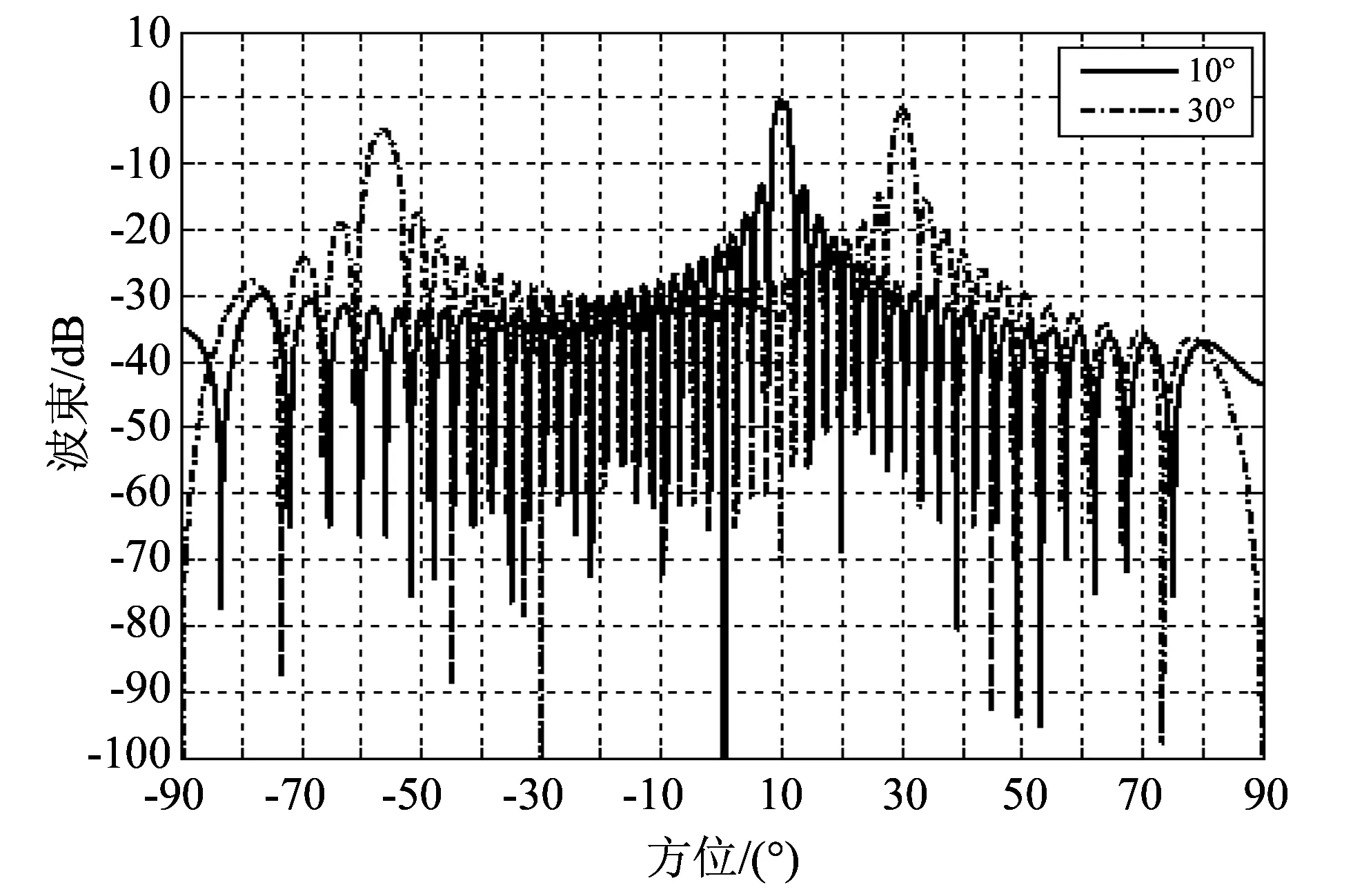
图 2 32阵元线列阵10°和30°方向图Fig.2 The directional pattern of 32 element linear array at 10 and 30 degrees

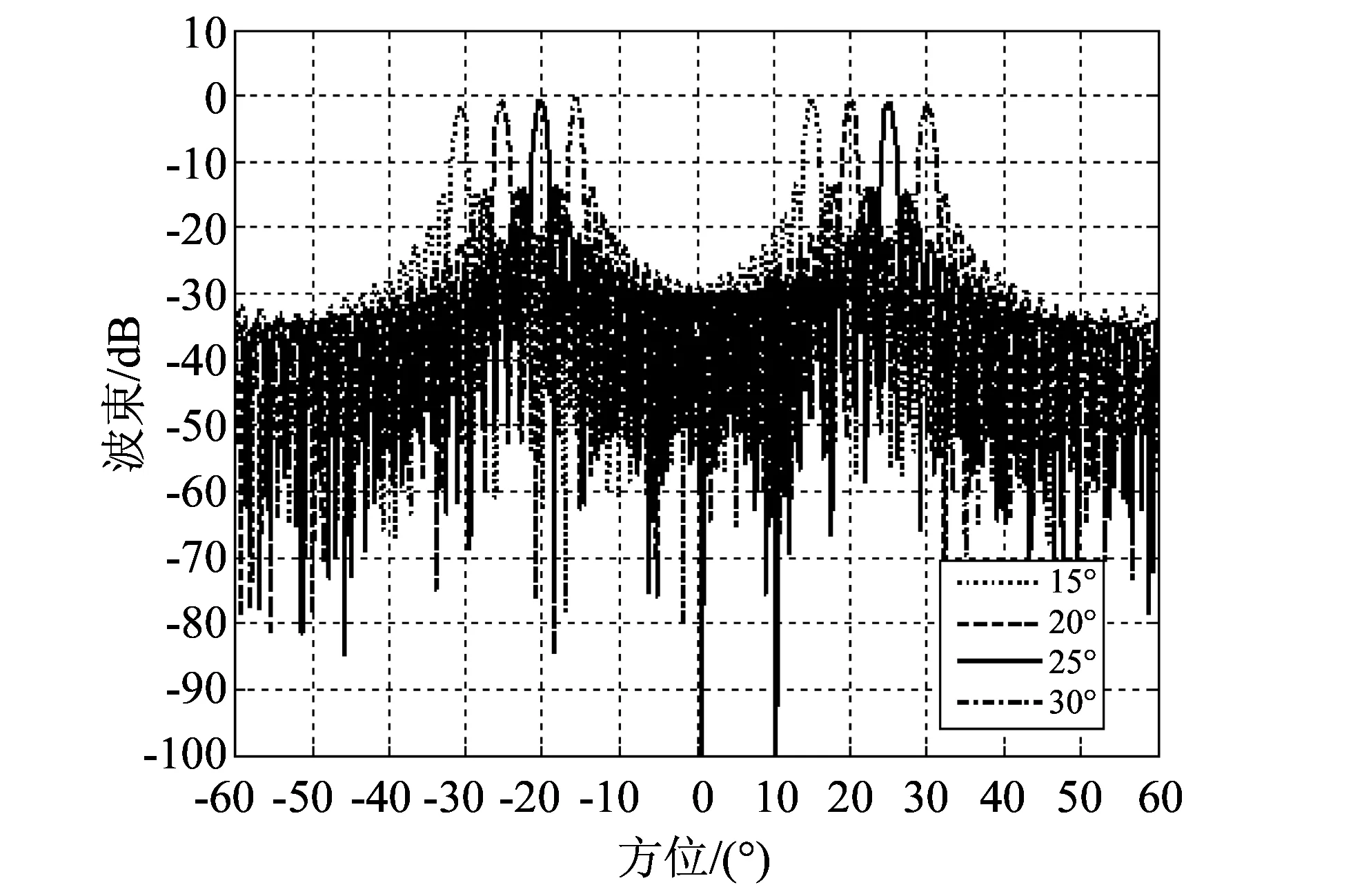
图 3 32阵元线列阵15°,20°,25°,30°方向图Fig.3 The directional pattern of 32 element linear array at 15,20,25,30 degrees

由图 3 可以看出， 该基阵产生的栅瓣效果较好. 当θ0=15°时，θm≈-30.8°； 当θ0=20°时，θm≈-25.4°； 当θ0=25°时，θm≈-20.4°； 当θ0=30°时，θm≈-15.6°. 即当主瓣以5°步长右移时， 栅瓣也以约5°的步长右移， 并且无论是主瓣还是栅瓣的波束宽度都在1.5°～2°之间， 指向性好.

2.2 加 权

为了降低旁瓣的影响， 改善阵列特性， 常用的方法就是加窗加权. 在窗函数的选择上， 应该尽量满足使主瓣窄、 使旁瓣低这两点要求. 在仿真过程中使用了Gauss， Hamming， Hanning， Chebyshev 4种加权方式， 处理结果如图 4～图 7 所示.

利用加权的方法降低旁瓣的同时通常都会使波束宽度增加. 通过对以上几种加权方式的统计比较， Gauss加权后的主瓣宽度约为2°； Hanning和Hamming加权后的主瓣宽度都大于2°， 且相邻主瓣间还有相互叠加； Chebyshev加权获得的主瓣宽度最窄， 小于2°， 并且旁瓣分布均匀.

图 4 Hamming加权后的方向图Fig.4 Hamming weighted image

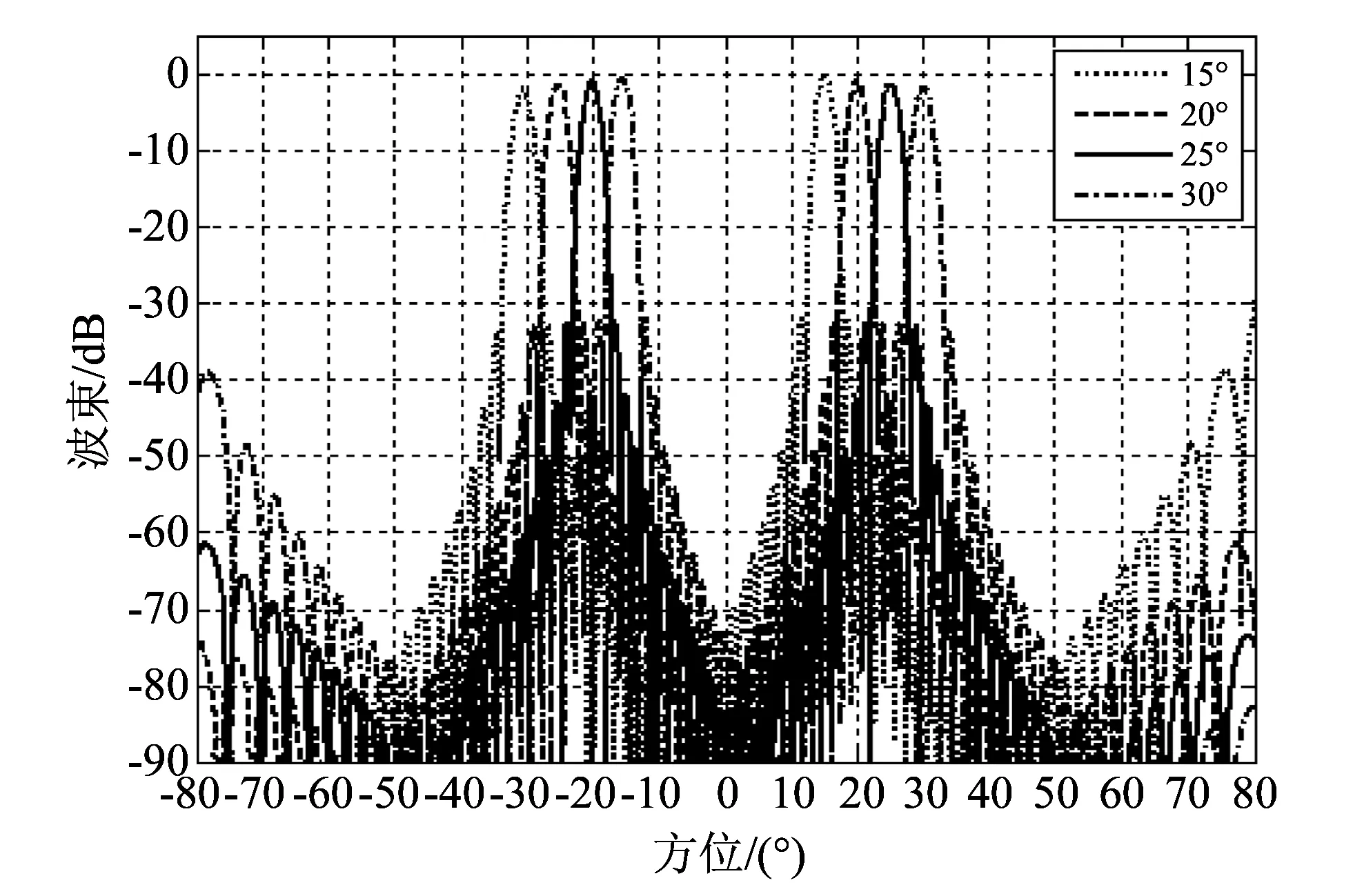
图 5 Hanning加权后的方向图Fig.5 Hanning weighted image

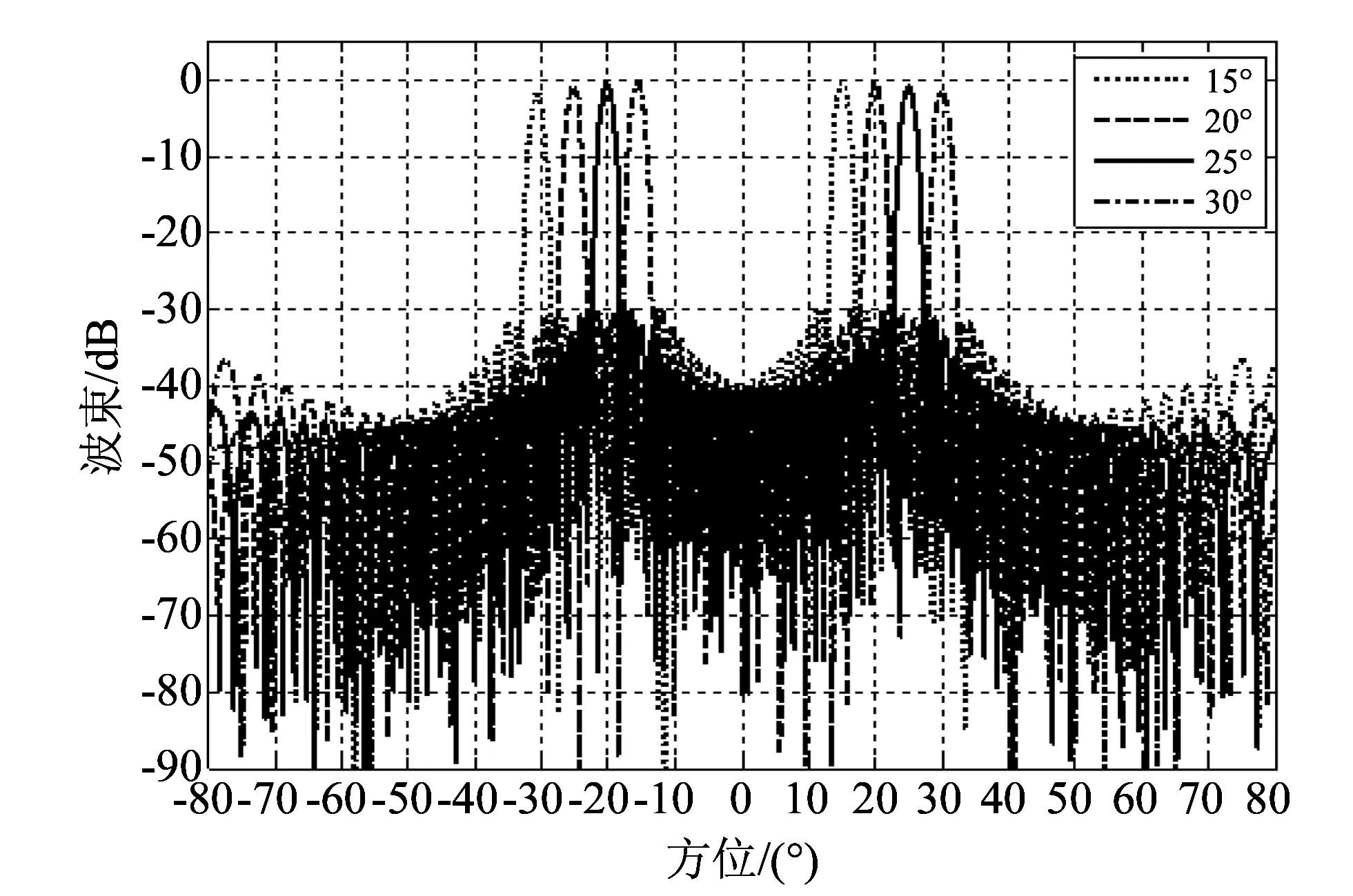
图 6 Gauss加权后的方向图Fig.6 Gauss weighted image

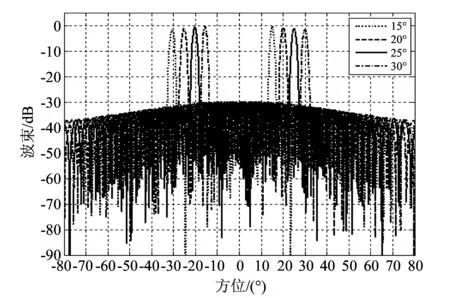
图 7 Chebyshev加权后的方向图Fig.7 Chebyshev weighted image

3 方法的讨论， 存在的问题

1) 栅瓣和主瓣并非同步线性变化.

图 8 32阵元线列阵45°方向图Fig.8 The directional pattern of 32 element linear array at 45 degrees

当主瓣的方向角以固定步长增加时， 栅瓣也随之增加， 但栅瓣变化的步长与主瓣变化的步长并非呈同步线性关系. 同时， 主瓣的幅值会逐渐减小， 栅瓣幅值会逐渐增加； 主瓣宽度会越来越大， 栅瓣宽度会越来越小. 因此， 在实际应用中并不是所有的栅瓣都可以利用， 需要根据实际情况加以选择.

2)当主瓣波束角较大时， 还会出现多个栅瓣.

如图 8 所示， 取阵元数N=32， 信号频率f=20 kHz， 阵元间距d=1.3λ， 阵元尺寸a=50 mm. 当主瓣的方向角θ0=45°时， 会出现两列栅瓣， 方向角分别为θm1≈-7.3°，θm2≈-63.6°.

以上现象会给实际应用带来一些问题， 例如， 扫描的扇面范围内有些角度无法利用栅瓣达到， 仍需要另行发射单波束. 并且阵元间距不宜过大， 过大会导致多个栅瓣出现， 不仅会分散发射能量， 而且增加了区分回波信号的难度.

4 结 论

本文对发射波束形成中的栅瓣现象做了分析研究， 提出了基于基阵特性提高声发射频次的方法， 用于改善传统多波束探测效率低的缺陷. 设计适当的阵元间距， 可以获得与主瓣特性相同的栅瓣， 实现单个线阵列同时向两个方向发射波束， 改变了传统应用中只能发射单波束的观念. 同时， 分别使用了几种加权方法来改善阵列特性， 对比出Chebyshev加权法效果最好. 虽然利用这种方法， 使得一个扇面内的某些角度无法利用栅瓣达到， 需要额外发射单波束， 但是， 对于实时测量的声纳来说， 已经极大地提高了发射速率和探测质量.

[1] 李启虎. 声纳信号处理引论[M]. 北京： 海洋出版社， 1985.

[2] Knight W C， Pridham R G， Kay S M. Digital signal processing for sonar[J]. Proceedings of the IEEE， 1981， 69(11)： 1451-1506.

[3] Veen B D V， Buckley K M. Beamforming： a versatile approach to spatial filtering[J]. IEEE Assp Magazine， 1988， 5(2)： 4-24.

[4] Kummer W H. Basic array theory[J]. Proceedings of the IEEE， 1992， 80(1)： 127-140.

[5] 管吉兴， 马瑞平， 黄巍， 等. 直线阵列数字波束形成技术[J]. 无线电工程， 2011， 41(9)： 25-27. Guan Jixing， Ma Ruiping， Huang Wei， et al. Digital beam forming technology for linear array[J]. Radio . Engineering， 2011， 41(9)： 25-27. (in Chinese)

[6] 罗玉兰， 景永刚， 许伟杰. 多波束形成方法及其实现[J]. 声学技术， 2007， 26(2)： 315-319. Luo Yulan， Jing Yonggang， Xu Weijie. Multi-beam forming technique and application[J]. Technical Acoustics， 2007， 26(2)： 315-319. (in Chinese)

[7] 李鹏飞， 彭东立. 相控阵ADCP编码信号相移波束形成[J]. 声学技术， 2015， 34(6)： 545-550. Li Pengfei， Peng Dongli. Coded signal phase shift beamforming of phased-array ADCP[J]. Technical Acoustics， 2015， 34(6)： 545-550. (in Chinese)

[8] 田坦. 声纳技术[M]. 哈尔滨工程大学出版社， 2010.

[9] 孙运强， 李在庭. 声阵列指向性函数计算[J]. 测试技术学报， 1996(2)： 719-724. Sun Yunqiang， Li Zaiting. Calculation of the pointing function of acoustic array[J]. Journal of Test and Measurement Technique， 1996(2)： 719-724. (in Chinese)

[10] 姚旭， 郭建中. 线阵阵元间距和宽度对波束指向性的影响[J]. 陕西师范大学学报(自科版)， 2010， 38(1)： 46-50. Yao Xu， Guo Jianzhong. Influence of linear array element width and element spacing on beam steering behavior[J]. Journal of Shaanxi Normal University (Natural Science Edition)， 2010， 38(1)： 46-50. (in Chinese)

[11] 林建， 马建敏， 庄子听. 换能器组阵对声场指向性的影响[J]. 噪声与振动控制， 2010， 30(3)： 55-59. Lin Jian， Ma Jianmin， Zhuang Ziting. Influence of transducer array on directivity of acoustic fields[J]. Noise and Vibration Control， 2010， 30(3)： 55-59. (in Chinese)

[12] 刘健康， 王莉， 鲁五一， 等. 影响超声换能器阵指向性的几个关键因素研究[J]. 压电与声光， 2013， 35(4)： 564-567. Liu Jiankang， Wang Li， Lu Wuyi， et al. Study on several key factors of fluencing the directivity of ultrasonic transducer array[J]. Piezoelectrics and Acoustooptics， 2013， 35(4)： 564-567. (in Chinese)

Study of Improving the Transmitting Frequency Method Based on the Array Characteristics

WANG Chen, GUO Yingge, WANG Runtian

(Shanghai Acoustics Laboratory, The Chinese Academy of Sciences, Shanghai 201815, China)

A new method is proposed to improve the transmitting frequency by using grating lobes, which could solve the problem of low detection efficiency. When the array element spacing is large, it is easy to produce grating lobes. When designing the array of transmit beam-forming, the close-packed array can avoid generating grating lobes, the complexity of the transmitter will increase. However, the existence of the grating lobe has its value. In this paper, MATLAB was used to simulate the pattern of the transmit beam forming. Summed up the change of the grating lobe and the main lobe. This paper introduced a method of transmitting beams in two different directions using a line array. Finally, weighting method was used to optimize the array characteristics.

transmit Beam-forming; array element spacing; grating lobes; multi-beam; Chebyshev weighting

2017-02-20

上海市科技创新行动计划资助项目(16DZ1205300)

王 晨(1990-)， 女， 硕士生， 主要从事声学技术的研究.

1671-7449(2017)04-0341-05

O429

A

10.3969/j.issn.1671-7449.2017.04.011