高炉煤气平均停留时间的模拟及讨论

郁肖兵，张 伟,2，李 强，邹宗树

(1. 东北大学冶金多相传输及反应工程研究所，沈阳110819；2. 武汉科技大学钢铁冶金及资源利用省部共建教育部重点实验室，武汉430081)

高炉煤气平均停留时间的模拟及讨论

郁肖兵1，张 伟1,2，李 强1，邹宗树1

(1. 东北大学冶金多相传输及反应工程研究所，沈阳110819；2. 武汉科技大学钢铁冶金及资源利用省部共建教育部重点实验室，武汉430081)

为了探究高炉煤气分布的规律，本研究在考虑料层分布的前提下使用三维高炉数学模型计算了煤气的平均停留时间.结果表明，料层分布对煤气流场影响明显，煤气平均停留时间和鼓风速度存在比较明显的线性关系.特别是对于1 850 m3的高炉在200 m/s的鼓风速度下，模型求得煤气平均停留时间约为6 s.此外，从几何相似的角度分析了几何模型的选择对模拟煤气平均停留时间的影响，得出了三维几何模型应为模拟煤气平均停留时间最优几何的结论.

高炉；煤气停留时间；煤气分布；数值模拟；三维

在高炉生产过程中，焦炭和含铁原料(矿石，烧结矿，球团矿)通过布料设备从炉顶加入，鼓风(温度可达1 000 ℃)通过风口围管及每个风口支管，进入高炉.由于压缩机提供的压强很大，热风具有很高的动能，进入高炉后会将风口前端的焦炭吹开，形成空隙度很高的风口回旋区，并裹挟焦炭在回旋区内运动和燃烧，同时产生大量的还原煤气(主要成分为CO).还原煤气随即向高炉中心和上部流动，随着热量的交换和Fe氧化物还原的进行，煤气成分不断发生变化，其中CO持续减少，CO2逐渐增多，煤气的还原势则不断下降，最后通过高炉顶部煤气上升管道离开高炉.与煤气接触的含铁原料，在下行的过程中，受到煤气物理热和还原势的影响，逐渐失去水分和氧元素，经历软化、熔融、滴落等过程，完成铁素和脉石的分离，汇聚于炉缸，最后以铁水和炉渣的形式排出高炉，至此高炉完成一个冶炼周期.

由于高炉炼铁过程是复杂的高温物理化学过程，再加上炉墙和冷却设备的包覆，造成高炉内部冶炼过程的不可视性，给冶金工作者掌握高炉内部冶炼规律带来很大困难.为了解决这类难题，冶金工作者开发了多种数学模型[1-13].相比于工业试验和半工业试验，高炉数学模型实施起来相对容易，耗费人力物力成本较低，并能得到高炉内部现象的细节性描述，从而有利于高炉的生产控制和过程优化.高炉内合理的煤气运动对冶炼过程的顺利进行具有重要的意义，而煤气速度分布能直观地反应高炉内部煤气流动状态，煤气停留时间亦能反应出煤气在高炉内部流动的快慢及煤气利用情况[14]，煤气停留时间过长，说明炉内存在煤气呆滞区；而停留时间过短，则可能意味着煤气利用率的下降或管道行程.前人已对高炉煤气停留时间做了一定的研究，如孙绍杰等人[10]通过使用85Kr作为示踪剂得到了2 580 m3高炉的煤气平均停留时间约为6.45 s，证明了实际工况下监测煤气停留时间的可行性；储满生等人[11]提及的高炉内煤气平均停留时间介于2～10 s之间；袁冬冬[12]、高攀等人[13]采用数值模拟的方法，对高炉内部料层进行简化处理，分别计算了二维和三维高炉的煤气停留时间，并应用停留时间分布理论求得了高炉内部死区的体积分数，但其未考虑料层交替排布和料面倾角变化对煤气流动的影响.本文建立的三维模型考虑了高炉内部料层分布对煤气流动的影响，并通过计算机模拟得到了高炉煤气平均停留时间分布的一些规律.此外，本文还简要讨论了不同几何模型的选择对煤气停留时间模拟的影响.

1 数值模拟方法

1.1 控制方程

气体连续性方程：

(εgρgUg)=0

(1)

气体动量方程：

(εgρgUgUg)=g-εg

(2)

气体组分传输方程：

(3)

体积分数方程：

εg+εs=1

(4)

在本模型中对示踪剂物理性质的处理是认为其与煤气性质完全一致，即便如此FLUENT仍可根据名字识别该示踪剂.考虑了湍流对煤气和示踪剂分布的影响，湍动能和湍动耗散率的计算采用标准κ-ε双方程模型.

1.2 炉料分布处理方法

考虑了布料操作对煤气流分布的影响，软熔带及其以上的炉料的料面函数根据文献[15]中提供的方法计算得出，料面分布模型计算得到的料面角度随料面编号(编号从炉喉料层往下逐渐增加)变化的关系曲线如图1所示.

图1 料面倾角变化图Fig.1 Change of the burden surface inclination angle

显性考虑了风口回旋区对煤气初始分布的影响，风口回旋区大小根据文献[16]提供的经验公式进行计算，为方便编程对回旋区进行球形简化处理.由文献[17]提供的高炉解剖数据，死料柱与水平面夹角取为45度.软熔带结构采用旋转二次曲面进行形状模拟，并考虑了影响煤气二次分布的软融层和焦炭层.模型中所使用的模拟条件列于表1.

另外，为了较为准确地模拟高炉内部的煤气流场，并尽量减少低质量网格所引起的迭代误差的影响(注：网格质量的高低和排列的规整程度直接影响速度场计算的准确性和云图的可视性)，基于ICEM划分BLOCK的方法，对高炉整体生成全六面体网格(并非基于轴对称或薄片结构或单个风口扇形几何)，并对风口区域进行单独加密，网格综合质量确保在0.85以上.

表1 模型所用参数和模拟条件

1.3 煤气停留时间测定方法

使用FLUENT获得煤气停留时间的总体思路与通过物理实验测定停留时间基本相当：即在反应器入口处(相当于本数值实验的风口位置)脉冲加入示踪剂，然后在反应器出口处(相当于本模型的炉顶出口)监测并记录示踪剂浓度随时间变化的数据.具体实现步骤如下：

第一步：使用模型计算得到稳态收敛的流场(此时入口示踪剂浓度为0)；

第二步：将模型改为非稳态，并将入口处示踪剂的组分浓度调整为单位1，然后求解脉冲时间内示踪剂的分布状态(此时相当于注入示踪剂的过程)；

第三步：示踪剂添加结束，将其在入口处的浓度重新调整为0，设置出口监测面以监测示踪剂浓度随时间的变化，随后求解示踪剂组分方程；

第四步：方程求解完毕，导出示踪剂数据并进行相应后处理计算.

2 结果及讨论

2.1 三维速度场分布

图2是鼓风速度为200 m/s时，风口轴线所在水平面(y=1.5)的煤气速度(表观速度)分布图，其中图2(a)所示的云图标尺为0～200，从云图中可以看出煤气速度变化跨度很大，在高炉内部中心区域煤气速度远远小于风口处的煤气速度，产生这种现象的主要原因可以由风量和横截面积的关系解释：轴线所在水平面的横截面积(模型中高炉炉缸直径为10.6 m)远大于风口总面积(风口直径为130 mm).为了清晰地显示风口前端煤气速度变化规律，将标尺区间选择为0～5，如图2(b)所示，从图中可以看出风口回旋区内的速度并非分布均匀，而是呈现出明显的梯度特征：越接近高炉中心，煤气速度越低；另外，速度梯度主要集中体现在回旋区内部.同回旋区内的特征相比，煤气在离开回旋区之后，速度梯度在轴向上明显减小，在圆周方向上则已看不出明显的速度差别(可以将此种分布近似看作沿高炉中心轴线呈轴对称分布)，这从侧面佐证了使用轴对称模型研究高炉的合理性.

图3是选取高炉内部几个典型的纵向、横向截面进一步探究煤气分布的规律.其中图3(a)展示的是相互垂直的两平面(x=0和z=0)上的煤气分布特征；图3(b)显示的是不同高度(20 m，18 m，14 m，12 m，8 m，6 m，1.5 m)对应的水平截面上的煤气分布.从图中可以较为清晰地观察出鼓风从进入到离开高炉的整个行程中所经过不同空间位置时的速度分布：煤气在炉内的低速区域集中在高炉中心部位死料柱和软熔带的熔融层(可参考图4(b))，而煤气速度较高的区域则存在于回旋区内部和炉喉中心部位.这种现象是高炉内部炉料分布对气体流动造成的综合影响的结果.从图3(b)可以看出同一水平面上的煤气速度分布并非一致，而是与炉料粒度、空隙度分布存在较为严格的对应关系：透气性差的区域，煤气速度相对低；透气性较好的区域，煤气速度相对也较高.

图4(a)是煤气速度矢量图，可以从图中看出高炉内部煤气的三次分布，即：回旋区作为煤气的发源地，是煤气的初始分布地带；软熔带焦炭层对煤气二次分布的水平导向作用；以及炉身处料层对煤气流分布的再整流作用.图4(b)显示的是模型计算所得到的煤气速度在0～0.5 m/s 之间的区域，可以看出这些区域主要集中在高炉中心死料柱和软熔带熔融层，并且从计算结果看，高炉中心死料柱的煤气流速度分布并非一致.

图2 风口横截面速度分布云图Fig.2 Velocity distribution contour on horizonal slice at tuyeres height

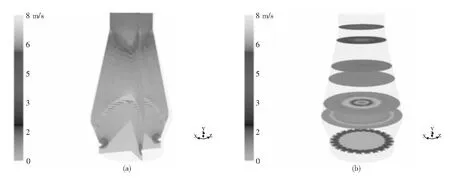
图3 高炉内几个典型截面速度分布云图Fig.3 Velocity distribution contour on several typical slices in the blast furnace

图4 速度分布矢量图和低速区云图Fig.4 Velocity vector and low-speed contour on vertical slice

2.2 三维压强场分布

图5是模型计算得到的压强(静压)分布图，从图中可以看出压强变化较大的区域是软熔带区域和回旋区内部，在这两个区域以外，高炉压强变化比较平缓；从图(b)可以看出同一水平截面上的压强也并非完全一致，即压强与炉料粒度，空隙度分布存在较为明显的对应关系.

2.3 煤气平均停留时间的计算及讨论

通过在风口处添加示踪剂(持续时间0.001 s)并在出口处实时监测示踪剂的质量分数，可以得出示踪剂质量分数随时间的变化关系，通过无因次化处理，即可得到不同鼓风速度所对应的停留时间分布曲线(RTD)，考虑到本文重点是对煤气平均停留时间规律的探究而非高炉RTD曲线本身特性的分析，故不再给出高炉煤气的RTD曲线.

(5)

从图6可以看出模型计算得到的高炉内煤气的平均停留时间与鼓风速度近似呈线性关系，其中在鼓风速度为150m/s时，停留时间约为8s，在鼓风速度为200m/s时，气体平均停留时间约为 6s，这与文献[10]中提供的测量数据具有一定的一致性.当鼓风速度继续增大，煤气的平均停留时间继续减小，但减小的幅度略微缩小.

图6 煤气平均停留时间与鼓风速度关系曲线Fig.6 Relation between average gas residence time and blast velocity

图6中A点为相同模拟条件下，使用二维几何模型求得的煤气平均停留时间，可以看出其数值与三维模型计算结果差别很大.这主要是由于计算域体积的差别使得二维模型不能完全替代三维模型；其次，二维模型的风口面积与实际不符，这会影响鼓风速度和鼓风量的确定.另外，从模型计算结果可以看出流场关于高炉中心近似呈轴对称分布，这说明可以使用轴对称模型模拟高炉现象.但轴对称模型得到的风口面积(4.32m2)约为实际风口总面积(0.32m2)的13.5倍(假设风口直径为130mm，炉缸直径为10.6m，风口数目为24).在保证鼓风总量不变的前提下，其鼓风速度或风口直径大约要降为原来的1/13.由计算可知煤气平均停留时间与煤气速度有很强的线性关系，降低煤气流速会使平均停留时间的求解不准确.另外，过窄的风口边界会对数值计算带来一定的影响.综上所述，全三维几何是模拟高炉煤气平均停留时间的最优几何.

高炉内煤气低速区的存在对冶炼是不利的，一方面它不能有效地传递还原所需的热量和还原剂，另一方面，会引起高炉单位生产成本的增加和内部空间利用效率的下降.为了进一步探究煤气低速区分布规律，通过数学方法统计出死料柱内低于煤气速度参考值(本文取0.1m/s)的区域体积，且认为煤气呆滞区或死区主要由该部分区域组成.模型求得死料柱内煤气低速区体积分数随鼓风速度的变化关系如图7所示.从图7可以看出，随着鼓风速度的增加，高炉中心死料柱内低速区的体积分数逐渐变小：对于鼓风速度为200m/s的操作条件，模型计算得出其中心死料柱内低速区的体积分数约为22%，对于300m/s的鼓风条件，其相应的煤气低速区比例变为15%.由厄根方程可知，大的鼓风动能必然伴随较大的沿程阻损，料柱中心煤气具有的动能是能量重新分配的结果.对于鼓风压强相对稳定且透气性较好的高炉(比如中心加焦操作)，热风受到阻力相对较小更容易吹透高炉中心，反之亦反.亦即鼓风速度或低速区比例(即停留时间分布曲线的“尾巴”)和鼓风压强应具有较强的对应关系.

图7 死料柱内低速区比例与鼓风速度关系曲线Fig.7 Relation between low-speed area percentage of deadman and blast velocity

高炉鼓风速度可以根据理想气体状态方程和工业生产数据(部分数据来源于参考文献[18])进行简化推导.通过推导可以近似得到大型高炉正常冶炼情况下鼓风速度的数值约为200m/s，在该入口条件下模型计算得到1850m3高炉的煤气平均停留时间计算约为6s.由于鼓风速度和煤气平均停留时间有较为明显的线性关系，当炉况失常(如：悬料或管道)时风口风压和鼓风动能会发生变化，煤气平均停留时间会相应地延长或缩短.如果能实现停留时间的准确测定并得到正常冶炼时可供参考的煤气平均停留时间，可以通过该指标的变化对炉况进行综合判断进而优化高炉炼铁操作.

本停留时间预测模型未考虑传热和化学反应的影响，得到的只是停留时间和煤气流速的半定量化关系.此外，炉缸煤气的生成和还原反应的发展均会对煤气量造成一定的影响.这部分气体在并入料层通道时会加快气体流速，进而会对煤气平均停留时间的确定带来影响，但这些影响因素的权重在文中并未予以考虑.

3 结 论

(1)构建了高炉煤气流分布模型，计算结果显示：高炉料层分布对煤气流场和压力场的分布影响明显，计算煤气停留时间应考虑料层分布的影响.

(2)半定量地确定了煤气平均停留时间与鼓风速度之间的关系，在鼓风速度为200m/s时，得到1 850m3高炉煤气平均停留时间约为6s.

(3)分析得出使用二维薄片几何和轴对称几何进行模拟的不足之处，指出三维几何是模拟高炉煤气平均停留时间的最优几何.

[1]Yagi J. Review: mathematical modeling of the flow of four fluids in a packed bed[J]. ISIJ International, 1993, 33(6): 619-639.

[2]Dong X F, Yu A B, Yagi J,etal. Modelling of multiphase flow in a blast furnace: recent developments and future work[J]. ISIJ International, 2007, 47(112): 1553-1570.

[3]Shen Y S, Guo B Y, Chew S,etal. Three-dimensional modeling of flow and thermochemical behavior in a blast furnace[J]. Metallurgical and Materials Transactions B, 2015, 46(1): 432-448.

[4]Shen Y S, Guo B Y, Chew S,etal. Modeling of internal state and performance of an ironmaking blast furnace: slot vs sector geometries[J]. Metallurgical and Materials Transactions B, 2016, 47(2): 1052-1062.

[5]Austin P R, Nogami H, Yagi J. A mathematical model for blast furnace reaction analysis based on the four fluid model[J]. ISIJ international, 1997, 37(8): 748-755.

[6]Ueda S, Natsui S, Nogami H,etal. Recent progress and future perspective on mathematical modeling of blast furnace[J]. ISIJ international, 2010, 50(7): 914-923.

[7]Dong X F, Yu A B, Burgess J M,etal. Modelling of multiphase flow in ironmaking blast furnace[J]. Industrial & Engineering Chemistry Research, 2008, 48(1): 214-226.

[8]Austin P R, Nogami H, Yagi J. A Mathematical model of four phase motion and heat transfer in the blast furnace[J]. ISIJ International, 1997, 37(5): 458-467.

[9]Dong X F, Yu A B, Chew S J,etal. Modeling of blast furnace with layered cohesive zone[J]. Metallurgical and Materials Transactions B, 2010, 41(2): 330-349.

[10]孙绍杰, 王喜来. 利用85Kr示踪剂对高炉内煤气运动的初步研究[J], 炼铁, 1984(1): 53-58. (Sun Shaojie, Wang Xilai. Preliminary study on coal gas movement in blast furnace with tracer 85Kr[J], Ironmaking, 1984(1): 53-58.)

[11]Chu M S, Yagi J, Shen F M. Modelling on blast furnace process and innovative ironmaking technologies [M]. Shenyang: Northeastern University Press, 2006: 13.

[12]袁冬冬. 氧气高炉工艺模型及煤气停留时间分布的研究[D]. 沈阳: 东北大学, 2012. (Yuan Dongdong. Study on process model of oxygen blast furnace and gas residence time distribution[D]. Shenyang: Northeastern University, 2012.)

[13]高攀. 氧气高炉工艺的数学物理模拟[D]. 沈阳: 东北大学, 2013. (Gao Pan. Mathematical and physical simulation on oxygen blast furnace process[D]. Shenyang: Northeastern University, 2013.)

[14]肖兴国, 谢蕴国. 冶金反应工程学[M]. 北京: 冶金工业出版社, 2008: 76. (Xiao Xingguo, Xie Yunguo. Metallurgical reaction engineering[M]. Beijing: Metallurgical Industry Press, 2008: 76.)

[15]杨天均, 徐金梧. 高炉冶炼过程控制模型[M]. 北京: 科学出版社, 1995: 10-24. (Yang Tianjun, Xu Jinwu. Control model of blast furnace smelting process[M]. Beijing: Science Press, 1995: 10-24.)

[16]曾华锋. 攀钢2000 m3高炉风口回旋区的研究[D]. 重庆: 重庆大学, 2007. (Zeng Huafeng. Investigation of tuyere raceway of BF 2000 m3for PISC [D]. Chongqing: Chongqing University, 2007.)

[17]鞍山钢铁公司钢铁研究所. 高炉内现象及其解析[M]. 北京: 冶金工业出版社, 1985: 15. (Ansteel Iron and Steel Research Institute. Phenomenon and analysis of blast furnace[M], Beijing: Metallurgical Industry Press, 1985: 15.)

[18]林成城, 项钟庸. 高炉炉型结构对煤气流分布影响[C]. 第七届中国钢铁年会论文集(上). 北京: 中国金属学会, 2009: 443-450. (Lin Chengcheng, Xiang Zhongyong. The influence of blast furnace type on gas distribution[C].Proceedings of the 7th China Iron and Steel Conference (1). Beijing: The Chinese Society for Metals, 2009: 443-450.)

Simulation and discussion on the average gas residence time in blast furnace

Yu Xiaobing1, Zhang Wei1,2, Li Qiang1, Zou Zongshu1

(1. Metallurgical Multiphase Transmission & Reaction Engineering Research Institute, Northeastern University, Shenyang 110819, China;2. Key Laboratory for Ferrous Metallurgy and Resource Utilization of Ministry of Education, Wuhan University of Science and Technology, Wuhan 430081, China)

In order to get a regularity of the gas distribution, the average gas residence time was calculated through a three-dimensional mathematical model of blast furnace (BF), taken into account of the previous calculation of the burden distribution. The results show that, the burden distribution pattern has an obvious impact on the gas flow field. There is an evident linear relationship between the average gas residence time and the blast velocity. Particularly, for the blast furnace of 1 850 m3, the average gas residence time is about 6 seconds at a blast velocity of 200 m/s. According to the similarity theory, effect of the model on the average gas residence time was analyzed. It was found that the three-dimensional model is an optimum one.

blast furnace; gas residual time; gas distribution; numerical simulation; three-dimensional

10.14186/j.cnki.1671-6620.2017.02.002

TF 537

A

1671-6620(2017)02-0083-07