基于多信息加权融合的降维航迹关联算法

王通

（昆明理工大学管理与经济学院，昆明650000）

基于多信息加权融合的降维航迹关联算法

王通

（昆明理工大学管理与经济学院，昆明650000）

针对分布式3个传感器多目标的航迹相关算法如果直接计算时间和花费都比较高这一问题，提出降维航迹关联算法。该算法先利用2个传感器的目标位置估计点构造航迹相关代价矩阵，求出最优解，再利用这个最优解与第3个传感器的目标位置估计点构建航迹相关代价矩阵，进一步得到三维航迹相关配对。针对单信息系统不稳定这一问题，提出了融合多个特征信息的加权算法。该算法利用熵权法赋予各种不同信息的权重进行加权融合，转化为单信息问题。仿真结果说明本文所给出的新算法不仅减小了目标跟踪误差而且其时间花费较少，因此，新算法是可行的。

多源信息融合；熵权法；降维；航迹关联

在分布式的多传感器追踪目标的过程中，单信息传感器的系统误差易造成航迹关联的混乱。因此，研究多信息的航迹关联是十分有必要的。

传统的航迹关联算法[1-3]一般不考虑传感器存在的误差，最近几年，国内外学者开始对多目标的关联与融合问题[4-12]进行了比较深入的研究。文献[13]采用动态规划和跟踪门技术提出一种新的全局最优航迹关联算法。文献[14-18]分别采用变权灰关联的方式、模糊平均综合相似度、图论、信息熵等不同的方式对信息进行融合及对算法进行改进。文献[19]是对多目标的数据关联进行研究。

与以往的文献不同，本文首先考虑了多个传感器采用降维的航迹关联算法；其次，将多个信息采用熵权法进行加权融合。将多信息转化为单信息问题，以达到减小误差，节省时间的目的。

1 系统描述

在离散时间状态下的目标变化的方程为：

式（1）中：T为目标个数；Fi(k)表示状态转移矩阵；Xi(k)代表目标i在k时刻的状态向量；Vi(k)是均值为零的、白色高斯过程噪声序列。

Fi(k)是已知的矩阵，且在运动过程中的不同时刻的噪声是相互独立。

离散时间系统的量测方程为：

式（2）中：Zj(k+1),j=1,2,…,mk为传感器在第j时刻的测量，mk表示第k时刻有效的跟踪测量的数量；H(k+1)为已知测量矩阵；Wi(k+1),i=1,2,…,T是均值为零的、白色高斯量测噪声序列，在不同的时刻量测之间的噪声是相互独立的。

维纳滤波理论是最早提出的最佳线性滤波理论，该理论的缺点是必须要用到过去的数据，需要保存大量过去的量测，增加了计算量。为了改善这个不足，本文采用卡尔曼滤波理论[20]。

2 多信息融合算法

2.1 熵权基本理论

熵权法的基本思想是应用信息熵获得各特征信息的熵权，再用这个熵权更改各个特征信息的权重，最终给各特征信息赋予不同的权重。

若系统有很多种特征信息，每个特征信息在系统中的概率为pi(i=1,2,…,n)时，于是该特征信息的熵的定义如下：

显然，当pi=1/n(i=1,2,…,n)时，即在各种特征的概率一样时，取最大熵为

由此可以看出，特征信息的熵值越小，说明特征信息的变异水平越大，系统可以得到较多的信息量，综合来看所有特征信息，熵值小的特征信息在系统中的作用也就越大，所以应该赋予较大的权重。反之，特征信息的熵值越大，说明特征信息的变异水平越小，系统可以得到较少的信息量，比较所有特征信息，应该赋予较小的权重。

最初的起始矩阵Δ，(Δji)n×m=[Δj1,Δj2,…,Δjm]是由第i(i=1,2,…,n)种信息指标的量测数据与第j(j=1,2,…,m)个目标数据差的绝对值Δj(i)=|Xo(i)-Xj(i)|确定，Δji代表第j个量测数据的第i种指标的绝对差。

求各特征信息的权重过程：

1）计算第i种特征的第j个量测在所有特征中所占的概率：

2）对概率取对数，并计算其信息熵：

3）根据特征信息的数量，计算系统最大熵：

4）计算第i种特征信息剩余度为：

量测信息在追踪目标过程中作用越大，则Di越大，给该特征信息赋予较大的权重。

5）用剩余度给该特征信息赋权：

2.2 基于熵权法的多源信息融合

模拟系统追踪n个目标，传感器可量测出状态等m个特征信息。多源信息利用熵权法的融合过程为：

1）分别求出系统中每个特征信息的关联度矩阵；

2）确定出来自相同量测的特征信息与目标的概率矩阵，并对其做归一化处理，构成新的矩阵为证据体；

4）如果特征信息是来自于相同的目标，则按照某个特征信息占总的比重对权重进行分配，确定出熵权证据体

求得的这个熵权证据体就将多个特征信息作为融合为一个特征信息，然后把它作为量测与目标之间的互联概率。

3 3个传感器的降维航迹关联算法

3.1 降维的航迹关联算法

在3个传感器跟踪目标的过程中，可以直接对三维的最优分配矩阵进行求解，但在跟踪的环境比较复杂时，直接对其求解不仅计算量繁琐，而且预测的精准度不高。因此，可以考虑两两降维的航迹关联算法，于是，提出改进的降维航迹算法（LD-TCA）。

LD-TCA算法的主要思想如下。

构建第1个传感器与第2个传感器目标状态估计点之间的统计距离。

确定2个系统的航迹关联代价函数：

式（11）中：i1=1,2,…,n1；i2=1,2,…,n2；s=1,2,3为系统编号；is=1,2,…,ns为系统s的航迹编号。

2个传感器之间就可以建立一个指派分配问题模型。

目标函数为：

约束条件为：

式（12）、（13）中：σi1i2=0代表第1个传感器的第i1个目标和第2个传感器的第i2个目标不是来自相同的目标；代表第1个传感器的第i1个目标和第2个传感器的第i2个目标来自相同的目标。

用匈牙利算法直接对以上的指派分配问题求解即可得到第1个传感器与第2个传感器的最优航迹关联对B，然后估计关联对B的目标位置。

估计点为：

式（14）中：s=1,2,3代表传感器编号；代表估计点的坐标。

下面构建nB个最优目标位置的估计点与第3个传感器的目标的状态估计点间的航迹关联代价矩阵，并确定指派分配问题模型。

统计距离为：

目标函数为：

约束条件为：

求解式（17）指派分配问题，确定出三维最优关联结果。

3.2 融合多信息加权的降维航迹关联算法

为减小误差，提高系统的适用性，下面将融合频率，脉宽，脉内重复周期等多个特征信息。提出了基于多源信息加权融合的降维航迹关联算法（MFLDTCA）。

算法步骤为：

1）计算各个目标特征信息的关联度矩阵，做归一化处理构成一个证据体，并计算对应相同目标的不同特征信息的权重，构成一个熵权证据体，得到融合多源信息后的互联概率矩阵，并分别定位目标在k时刻的位置；

2）构建在k时刻第1个传感器与第2个传感器的目标定位点间的航迹关联代价矩阵函数，建立指派分配数学模型；

3）利用匈牙利算法求解上述模型，得到第1个传感器与第2个传感器的最优航迹关联对；

4）估计3）中最优航迹关联对的目标状态的位置；

5）利用4）中所得的目标状态位置的估计点和第3个传感器的目标定位点根据统计距离构建代价矩阵函数，建立指派分配数学模型；

6）同样利用匈牙利算法求解模型，得到三维最优航迹关联组合，确定出最优解；

7）利用卡尔曼滤波对6）的最优解所对应的目标状态进行下一时刻的目标状态预测。

4 仿真与分析

4.1 仿真环境

设仿真系统有3个传感器，采用分布式结构。仿真在跟踪8个目标的过程速度为20 m/s，且受噪声的干扰。目标的间距分别为800 m和400 m，目标起始状态位置的产生是按正态分布，目标起始状态位置的航向产生是在0～2π之间按均匀分布。扫描周期为2 s，仿真10次，仿真150步。

4.2 仿真结果分析

4.2.1 最优航迹与降维航迹关联算法比较

1）目标间距d=800 m时，2种算法的均方根误差仿真见图1、2。

2）目标间距d=400 m时，2种算法的均方根误差仿真见图3、4。

由图1～4可知：

1）当测距测角的误差相同时，随着距离的减小，LD-TCA均方根变化幅度更大，LD-TCA的误差也越大，LD-TCA算法不如D-TCA；

2）当目标间距相同时，在测距测角的误差增大的情况下，LD-TCA算法的均方根大，说明当探测条件一般时，LD-TCA的稳定性较差，因此，LD-TCA的误差也就比D-TCA的误差大；

总之，当探测条件不好时，单信息的降维航迹关联算法（LD-TCA）不如直接对3个传感器求最优解（D-TCA）准确，为提高系统的精确性，可以考虑增加多特征信息。

4.2.2 单信息与多信息的降维航迹关联算法比较

1）目标间距d=800 m时，2种算法的均方根误差仿真见图5、6。

2）目标间距d=400 m，2种算法的均方根误差仿真见图7、8。

由图5～8可以得到如下结论：

1）当间距相同时，在测距测角误差增大的情况下，融合多源信息的降维的航迹关联算法（MFLDTCA）比单信息的降维航迹关联算法（LD-TCA）的均方根小，因此，MFLD-TCA算法的准确度高；

2）当测距测角误差相同时，随着距离的减小，LDTCA的均方差变化的幅度更大，因此，LD-TCA算法的误差也比较大，效果不如融合多信息的MFLD-TCA算法。

综上所述，测探条件一般时，融合多信息后，误差明显减小，因此，MFLD-TCA的算法比LD-TCA的算法更好。

4.2.3 算法运行时间的比较

目标间距d=800 m，测距误差er=200 m，测角误差eθ=0.02rad时，不同目标数情况下算法时间耗费对比见表1。

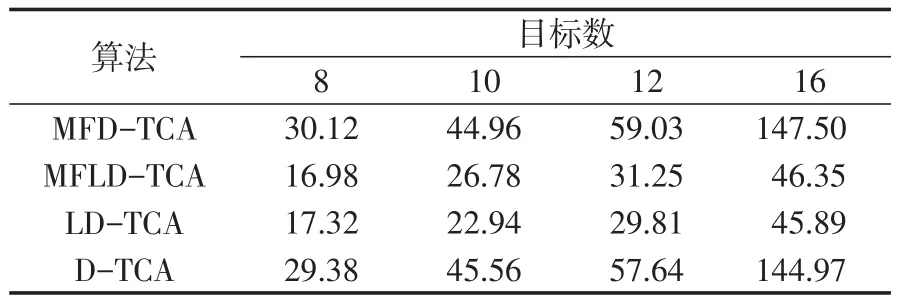
表1 不同目标数情况下算法时间耗费对比 sTab.1 Comparison of time cost of different target numbers

由表1可以得到：无论有多少个目标，运行花费时间少的都是LD-TCA，并且其融合多源信息后的算法MFLD-TCA的花费的时间也较其他算法的短，说明用降维的航迹关联算法比直接用三维的求解最优的航迹关联算法能够有效节省时间。

此外，与单信息的算法相比，融合多源信息后增加的时间花费并不多，但是融合多源信息后，航迹关联的准确性提高了，并且在系统的探测情况较差的时，增加了系统的稳定性和适应性。

5 结语

本文主要提出了基于两两融合的降维航迹关联算法。通过降维，使三维及以上的分配问题转化为二维指派分配问题，不仅节省了时间，而且使系统在恶劣的探测环境下提高了精准度，提升了系统跟踪多目标的定位的准确度。

由算法分析和仿真实验的结果可以看出，与直接求解的多维最优分配问题比较，本文所提出的降维航迹关联算法不仅提高航迹关联质量，而且使程序的计算量和时间花费有所降低，相比三维及以上分配来说，降维分配思想使时间复杂度降低了，是一种比较可靠的求解算法。

此外，在基于单特征状态信息的基础上，又融合了频率、脉宽、脉冲重复周期等特征信息，使得融合多源信息的降维航迹关联算法优化和改善了单信息的航迹关联算法，使算法更接近于实际，减小了目标追踪误差，优化了其性能，保证了其可行性。

[1]何友，王国宏，关欣.信息融合理论及应用[M].北京：电子工业出版社，2010：45-78. HE YOU，WANG GUOHONG，GUAN XIN.Information fusion theory with applications[M].Beijing：Publishing House of Electronics Industry，2010：45-78.（in Chinese）

[2]潘泉，梁彦，杨峰，等.现代目标跟踪与信息融合[M].北京：国防工业出版社，2009：89-167. PAN QUAN，LIANG YAN，YANG FENG，et al.Modern target tracking and information fusion[M].Beijing：National Defense Industry Press，2009：89-167.（in Chinese）

[3]SHALOM Y B.On the track-to-track correlation problem [J].IEEE Transactions on Automatic Control，1981，26（2）：571-572.

[4]DONOHO D L，JOHNSTONE I M.Ideal spatial adaptation via wavelet shrinkage[J].Biometrika，1994，81（12）：425-455.

[5]DONOHO D L.De-noising by solf-thresholding[J].IEEE Transactions on Information Theory，1995，41（3）：613-627.

[6]FERRY J P.Exact bias removal for track-to-track association problem[C]//12thInternational Conference on Infor-mation Fusion.2009：1642-1649.

[7]CROUSED F，BAR SHALOM Y，WILLETT P.Sensor bias estimation in the presence of data a association uncertainty[C].Signal and Data Processing of Small Targets，2009：1-22.

[8]熊伟，高峰，王海鹏.系统误差下航迹关联算法[J].火力与指挥控制，2012，37（11）：29-32. XIONG WEI，GAO FENG，WANG HAIPENG.Research of trach association with systematic errors[J].Fire Control and Command Control，2012，37（11）：29-32.（in Chinese）

[9]CHANG C B，YOUENS L C.Measurement correlation for multiple sensor tracking in a dense environment[J]. IEEE Transactions on Automatic Control，1982，27（6）：1250-1252.

[10]潘泉.多源信息融合理论及应用[M].北京：清华大学出版社，2013：1-21. PAN QUAN.Multi-source information fusion theory and its applications[M].Beijing：Tsinghua University Press，2013：1-21.（in Chinese）

[11]郭慧勇.多传感器信息融合技术的研究与进展[J].中国科学基金，2005，1（1）：17-21. GUO HUIYONG.Researches and advances in multi-sensor information fusion technology[J].Bulletin of National Natural Science Foundation of China，2005，1（1）：17-21.（in Chinese）

[12]孙辉，赵峰，张锋云.多传感器信息融合技术及其应用[J].海洋测绘，2009，29（5）：77-81. SUN HUI，ZHAO FENG，ZHANG FENGYUN.The technology and application of multisensor information fusion [J].Hydrographic Surveying and Charting，2009，29（5）：77-81.（in Chinese）

[13]权义宁，姜振，黄晓东，等.一种新的数据融合航迹关联算法[J].西安电子科技大学，2012，39（1）：67-74. QUAN YINING，JIANG ZHEN，HUANG XIAODONG，et al.Study a new track correlation algorithm in data fusion[J].Journal of Xi’an University，2012，39（1）：67-74.（in Chinese）

[14]李楠，王春雷，胡锦涛，等.变权灰关联分布式传感器信息融合的辐射源识别[J].中国电子科学研究院学报，2013，8（3）：17-21. LI NAN，WANG CHUNLEI，HU JINTAO，et al.Distributed sensors information fusion identification based on adaptive weight grey correlation algorithm[J].Journal of China Academy of Electronics and Information Technology，2013，8（3）：17-21.（in Chinese）

[15]宋国栋.求多目标决策加权和权系数的图论方法[J].控制与决策，1987，2（3）：23-27. SONG GUODONG.Strives for the multi-target decision weighting and weight coefficient method of graph theory [J].Journal of Control and Decision，1987，2（3）：23-27.（in Chinese）

[16]鲍新中，张建斌，刘澄.基于粗糙集条件信息熵的权重确定方法[J].中国管理科学，2009，17（3）：131-135. BAO XINZHONG，ZHANG JIANBIN，LIU CHENG.A new method of ascertaining attribute weight based on rough sets conditional information entropy[J].Chinese Journal of Management Science，2009，17（3）：131-135.（in Chinese）

[17]曾昭博，王睿，刘伟，等.基于模糊平均综合相似度的航迹关联算法[J].电讯技术，2009，49（8）：9-12. ZENG ZHAOBO，WANG RUI，LIU WEI，et al.A data association algorithm based on fuzzy mean synthetical resemble degree[J].Telecommunication Engineering，2009，49（8）：9-12.（in Chinese）

[18]尤天慧，樊治平.区间数多指标决策中确定指标权重的一种客观赋权法[J].中国管理科学，2003，11（2）：92-95. YOU TIANHUI，FAN ZHIPING.An objective method for determining attribute weights in multiple attribute decision making with intervals[J].Chinese Journal of Management Science，2003，11（2）：92-95.（in Chinese）

[19]叶西宁.多目标跟踪中数据关联与多维分配技术研究[D].西安：西北工业大学，2003. YE XINING.A study of data association，multi-dimension assignment problem in multi-target tracking[D].Xi’an：Northwestern Polytechnical University，2003.（in Chinese）

[20]刘胜.最优估计理论[M].北京：科学出版社，2011：1-36. LIU SHENG.The optimal evaluation theory[M].Beijing：Science Press，2011：1-36.（in Chinese）

Low Dimension Track Correlation Algorithm Based on Multi-Source Information Weighted Fusion

WANG Tong
（Faculty of Management and Economics,Kunming University of Science and Technology,Kunming 650000,China）

Low dimension track correlation algorithm was proposed to solve the high cost and long time problem of track correlation algorithm which aimed at distributed three sensors multi-target.This algorithm used,first of all,the estimated point of the two sensors’target position to construct the cost matrix of track correlation,to obtain the optimal solution;then reused this optimal solution and the estimated point of the third sensor’s target position to construct the cost matrix of track correlation,to further obtain the three-dimension track correlation pairing.To solve the instability problem of single information source,in this paper,the algorithm of multi-information weighted fusion.This algorithm used the entropy weight method giving weight to information of various weighted fusion was proposed,transforming multi-information issue into single information issue.The simulation results showed that the new algorithm proposed in this paper not only reduced the tracking error of the target but also spent less time,demonstrating the effectiveness of the new algorithm.

multi-source information fusion;entropy weight method;low dimension;track correlation

V448.2；TN957

A

1673-1522（2017）02-0192-07

10.7682/j.issn.1673-1522.2017.02.003

2017-02-16；

2017-03-22

王通（1992-），女，硕士。