不等式部分的高考复习策略
辽宁省实验中学 成建卓

不等式问题广泛存在于高中数学的各个领域,除了一些单纯的不等式问题外,在立体几何、三角函数、数列、解析几何、函数与导函数等部分都涉及不等式及相关数学思想,因此不等式是高考复习的一个重点.
《考试说明》中对不等式部分的要求是:
1.不等关系
了解现实世界和日常生活中存在着大量的不等关系,了解不等式(组)的实际背景.
2.一元二次不等式
(1)会从实际问题的情境中抽象出一元二次不等式模型.
(2)通过函数图像了解一元二次不等式与相应的二次函数、一元二次方程的联系.
(3)会解一元二次不等式,对给定的一元二次不等式,会设计求解的程序框图.
3.二元一次不等式组与简单线性规划问题
(1)会从实际情境中抽象出二元一次不等式组.
(2)了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组.
(3)会从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决.
(1)了解基本不等式的证明过程.
(2)会用基本不等式解决简单的最大(小)值问题.
一、关于不等式的性质
在不等式的基本性质中,我们最常用的是
(1)若 a>b,则 a+c>b+c.
(2)若 a>b,c>0,则 ac>bc.
需要说明的是,以上两个性质,不仅是不等式变换的手段,更是解决相关不等式的方法.

【解析】很明显,需要运用不等式的性质对已知不等式进行变换.
解法1:一个很直接的想法是应用性质(1),对已知不等式去分母,即同时乘以(b+c)(a+c)(a+b)可得

化简可得
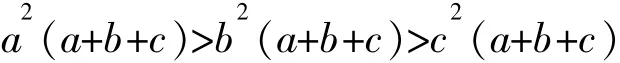
由于 a,b,c∈R+,故得 a>b>c.
想法很直接,但运算略有麻烦,是否有更简单的方法呢?
解法2:运用性质(1),在已知不等式中各项同时加 1,即
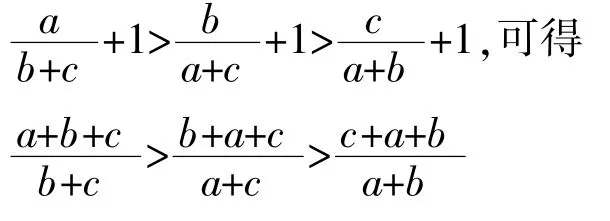

所以 b+c<a+c<a+b,
故得 a>b>c.
解法3:同样是加1,可以考虑先取倒数,当然,道理是相同的.
由已知得

二、关于运用平均值不等式解决简单的最大值和最小值问题
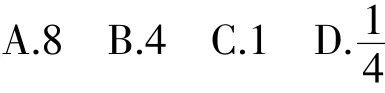
【答案】B
【解析】因为 3a·3b=3,所以 a+b=1,

解法3:对于解法2,也可以不乘开,分别运用均值不等式,即

A.1 B.2 C.3 D.4
【答案】D
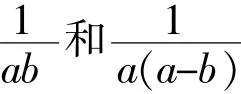
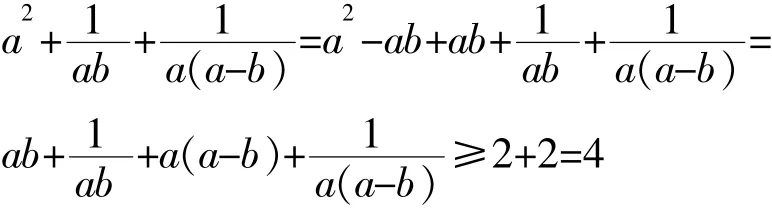
当且仅当 ab=1,a(a-b)=1 时“=”成立,
例4 设x,y为实数,若4x2+y2+xy=1,则2x+y的最大值是____.
【解析】这个问题入手前需要仔细观察,2x+y为和的形式,怎么会有最大值呢?故不能去寻求2xy的定值,而是根据已知条件,把2x+y作为一个整体,寻找不等关系.
由已知条件


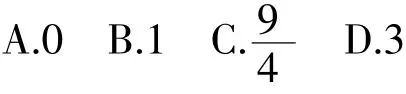
【答案】B
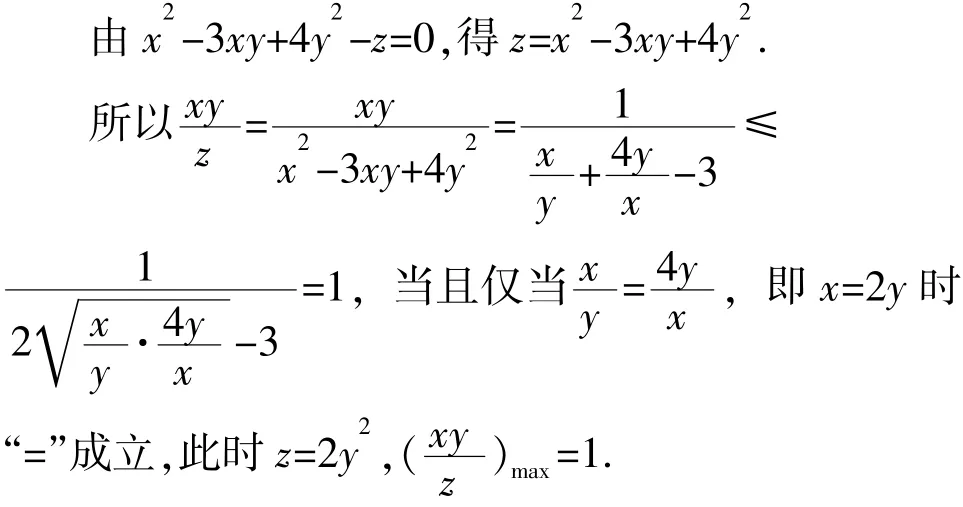
这个过程是用已知积的形式,去构造和的定值.
三、关于线性规划中的开放性问题
在线性规划问题中,已知线性约束条件,求目标函数的最值问题为基本问题,而以线性约束条件为问题情境,结论为开放形式的问题往往具有一定的综合性.

【答案】A

由不等式表示的平面区域可知,当直线ax+by=z(a>0,b>0)过直线 x-y+2=0 与直线 3x-y-6=0 的交点(4,6)时,目标函数 z=ax+by(a>0,b>0)取得最大12,即4a+6b=12,所以2a+3b=6,这与前面讲到运用1的逆代去求最值是一致的.
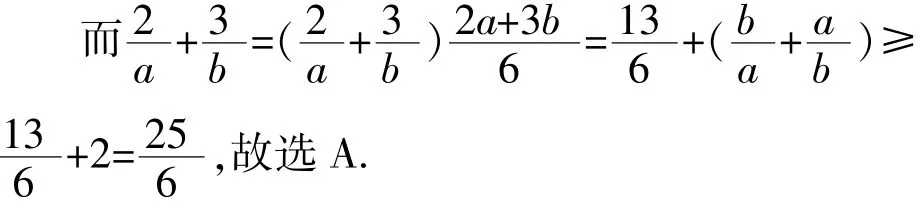

【答案】B
【解析】问题的关键是画对可行域,并运用简单的几何知识解决问题.


不等式问题还涉及二次不等式、不等式的应用等内容,笔者将在以后的文章中阐述.

