基于线状系统的长江干线运输船舶洗舱站选址研究

林 桦，李表奎，徐培红

（1.武汉理工大学，湖北 武汉 430063；2.长江航务管理局，湖北 武汉 430014）

基于线状系统的长江干线运输船舶洗舱站选址研究

林 桦1，李表奎1，徐培红2

（1.武汉理工大学，湖北 武汉 430063；2.长江航务管理局，湖北 武汉 430014）

长江干线散装危险品运输逐年增加，需要配套建设船舶洗舱站点。在学者研究的基础上，将长江干线23个主要港口进行洗舱需求区段划分，引入线状系统的概念，建立了均匀系统中维护点最佳分布模型，通过基础数据的分析及预测，对模型进行求解，提出长江干线散装液体危险品船舶洗舱站选址方案。

线状系统；长江干线；散装液体危险品；洗舱站；选址

1 引言

随着经济的快速发展，各类化工产品的需求快速增加，长江干线散装危险品运输随之增加，目前长江干线洗舱站仅有5个，分布在重庆、武汉和南京，洗舱能力不足，洗舱压力大，大量的油品和化学品运输为船舶安全营运及内河水域的环境保护带来严峻挑战，需要对干线洗舱站点进行重新布局规划。长江干线危险品船舶洗舱站的选址研究，将为长江生态修复和绿色发展提供途径和思路，为长江干线危险品洗舱站布局规划的顶层设计提供理论参考。

Erdemir和Rajan等[1-2]研究了考虑点状需求和线状需求的集合覆盖选址问题，分别建立隐式模型和显式模型，并设计了启发式算法对其进行求解。周建勤[3]研究了成本导向的线状需求物流节点连续选址问题，并通过构建单一物流节点选址模型求出了模型的最优解。张其兵[4]分析了长江危险品水上运输的发展现状，并对水上运输安全系统采用集对分析的方法进行表达，建立了长江危险品水上运输安全集对分析评价模型。贾禹[5]阐述了内河危险品运输服务链运作流程，并选取重庆市危险品的运输案例进行了成本结构的分析和优化。李娜[6]针对选取基于交通流的综合事故率、死亡率作为系统安全状态方程模型的指标变量，建立了水上交通安全状态方程。

本文在学者研究的基础上，将长江干线23个主要港口进行洗舱需求区段划分，引入线状系统概念，并构建线状系统维护点最优分布模型，通过模型求解分析得出洗舱站选址方案。

2 选址模型建立及求解

2.1 选址模型

现实世界中有很多在一条线上分布的系统，如铁路、公路、输油管线、输电线路等，称为线状系统。根据系统中单位长度的维护费用是否相同，可将线状系统分为均匀线状系统和非均匀线状系统。均匀系统是指系统中任何地方单位长度的维护费用相同的理想系统，在均匀系统中，站点的管辖范围相等。然而实际上，系统由于受自然条件、经营条件、基础设施状况等外在环境的影响，单位长度维护费用不同，这样的系统就为非均匀系统。

2.1.1 非均匀系统的转化。均匀系统和非均匀系统的区别体现在系统中单位长度维护成本的不同，因此在已知线状系统长度和单位长度维护成本的条件下，可以实现将非均匀系统向均匀系统的转化。

例如非均匀线状系统总长为S，由S1和S2两段组成，单位长度的维护费用分别为c1、c2(c1≠c2)。假设转化后的均匀系统单位长度的维护费用为c，那么转化后系统长度存在以下关系：

这样，由S1和S2两段组成的非均匀系统就转化为总长为S'，单位长度维护费用为c的均匀系统。

2.1.2 均匀系统站点的最优分配。系统中站点的分配需要解决的问题是建立多少个站点，建在何处，以全面覆盖线状系统中所有区域，同时使站点建设总耗费最小。由于非均匀系统可以实现向均匀系统关系转化，因此研究均匀系统站点的最优分配将对解决实际系统中站点配置分布具有指导意义。

均匀系统有两个特征：单位长度维护费用相同、站点管辖范围相等。解决站点分配中的问题可根据均匀线状系统的特点，建立以总成本最低为目标的系统站点分配模型，确定站点建设数目、站点位置、站点管辖范围等，如图1所示。

图1 均匀系统主要参数示意图

（1）参数设置

S-均匀线状系统总长；

n-均匀线状系统中站点个数；

F-站点建设的固定成本；

d-站点两侧管辖范围(d≤x)；

d'-站点两侧超出d管辖范围以外的长度；

c-站点两侧d'以内的单位维护费用；

c'-每超出d'的单位维护费用增加值；

Pi-系统中全部站点成本(i=1,2,3)。

（2）目标函数

另外，成本函数的表达式分别为：

P1-系统内全部站点固定成本：

P2-系统内全部站点管辖范围d内的维护成本：

P3-系统内全部站点管辖范围d以外的维护成本：

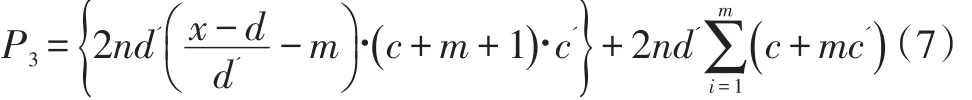
2.2 基础数据

选址模型基础数据主要包括船舶洗舱需求量、洗舱站建设成本以及洗舱需求区段划分等。

2.2.1 洗舱需求。目前，船舶洗舱需求主要包括两类：船舶货物换装洗舱和船舶上坞检修洗舱，2015年长江沿线各省船舶换货种洗舱需求约为3 000艘次/年，需上坞检修的船舶约为1 400艘次/年。洗舱站建设成本包括固定成本和可变成本，其中固定成本参考已有洗舱站的投资标准，计算取值2 000万元。2020、2030年洗舱需求预测值见表1，2020、2030年船舶上坞检修洗舱需求总量分别为1 700艘次和1 600艘次（2030年船舶平均吨位将增加，使得实际船舶艘数减少）。

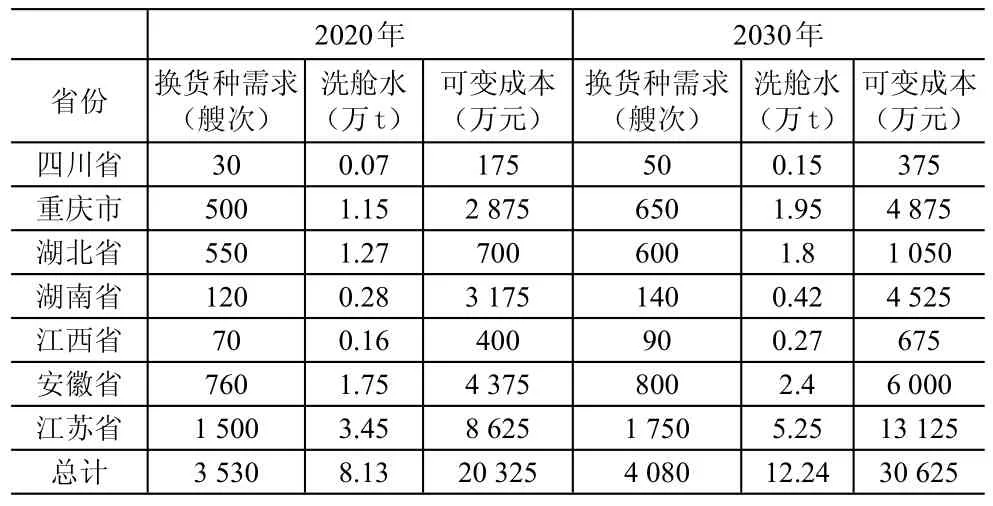
表1 洗舱需求预测值

2.2.2 洗舱需求区段划分。长江干线港口位置间隔里程为港口间实际距离，但是危险品船舶洗舱需求与多种因素有关，船舶洗舱需求区段和港口间实际距离不能等同。本文以港口状况、运输能力及经济水平为准则，构建港口物流综合能力评价体系，运用熵权法计算物流综合能力评分，作为洗舱需求区段划分的依据。评价结果见表2。

洗舱需求区段是在23个主要港口间实际里程的基础上，以物流综合能力评分为权重计算划分所得到的区间范围，即将港口之间的实际里程转化为计算里程，见表3。

2.3 模型求解

计算求解所需要的数据都已确定，运用JDK环境下的Java语言编写程序并求解，得到n取不同值时的目标函数。见表4和图2。

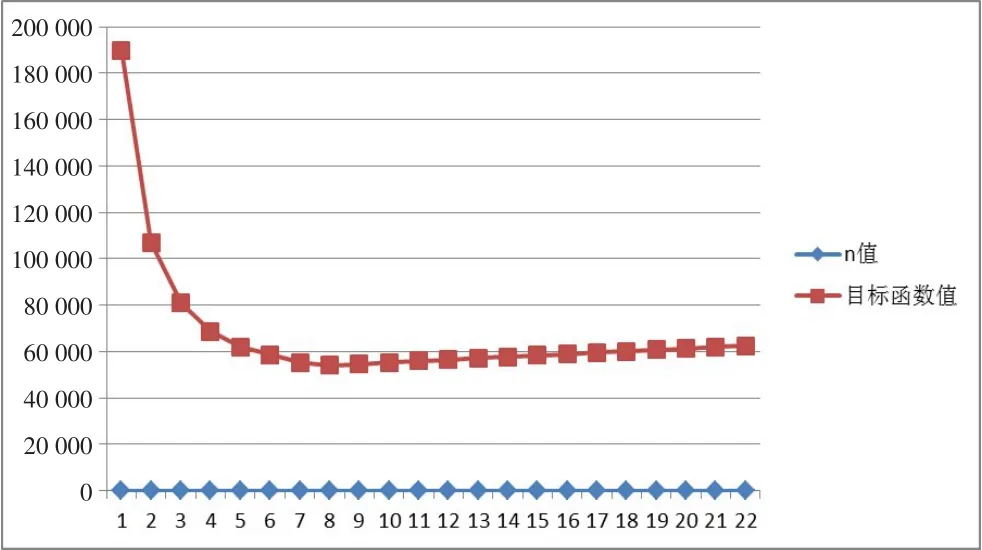
图2 目标函数曲线图

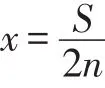
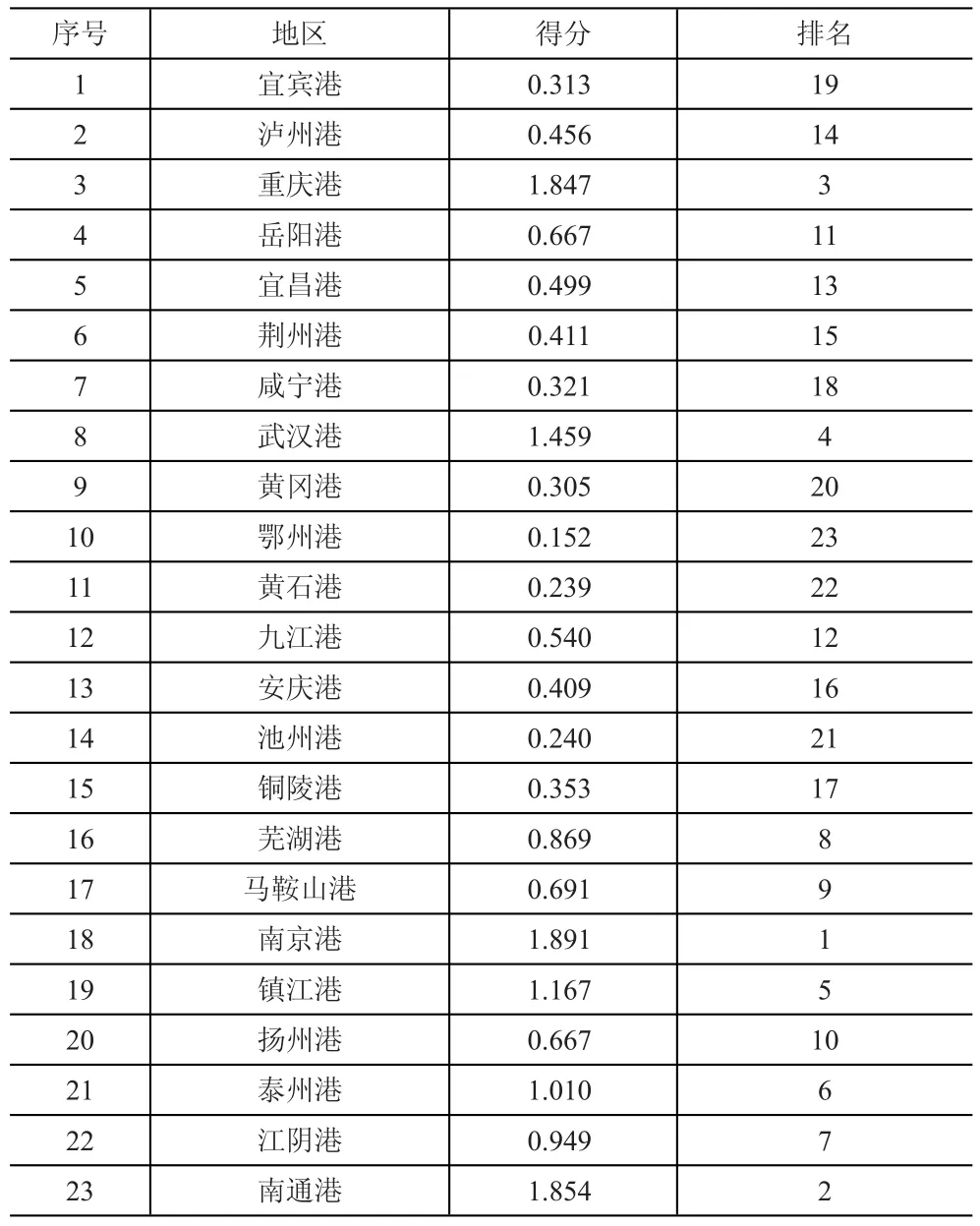
表2 长江干线主要港口物流综合能力评价得分表

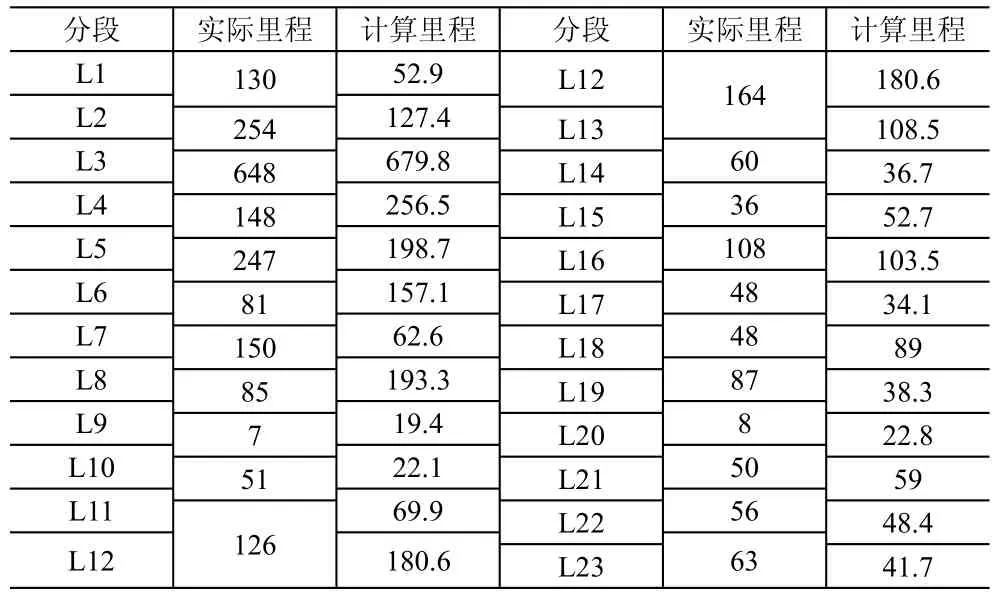
表3 实际里程与计算里程转化表（km）

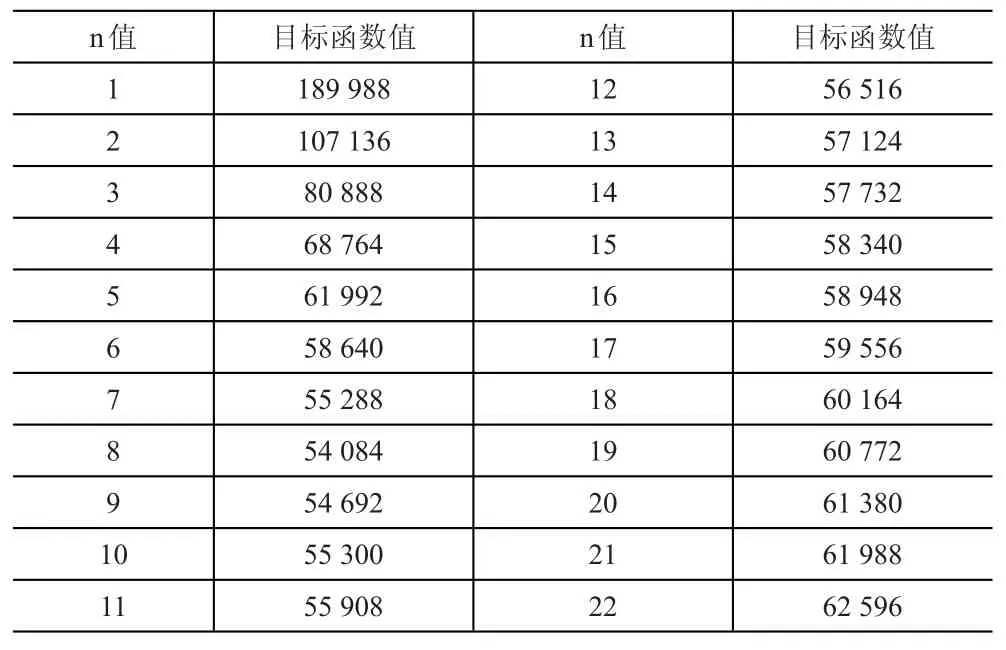
表4 不同n值下的目标函数值

表5 线状系统站点分配表

3 选址方案

3.1 站点规模

长江干线散装液体危险品船舶洗舱站规模和数量的确定需要考虑长江干线散装液体危险品船舶洗舱发展需求及长江岸线资源、通航条件。

根据未来长江干线航道通航条件、危险品船舶船型尺度、船舶洗舱需求量等要求，结合不同区域洗舱站的不同自然环境条件等因素，以库区上游建设小型、库区及长江中游建设中型、长江下游兼顾海轮等不同需求为导向，结合现有洗舱站建设情况，初步确定洗舱站污水接收中转能力及年洗舱能力，确保能够满足长江干线未来洗舱需求，按照可停靠危险品船舶核定载重吨为标准，将长江干线散装液体危险品船舶洗舱站划分为三种规模：可停靠船舶核定载重吨为3 000t级为小型，5 000t级为中型，50 000t级为大型，详见表6。

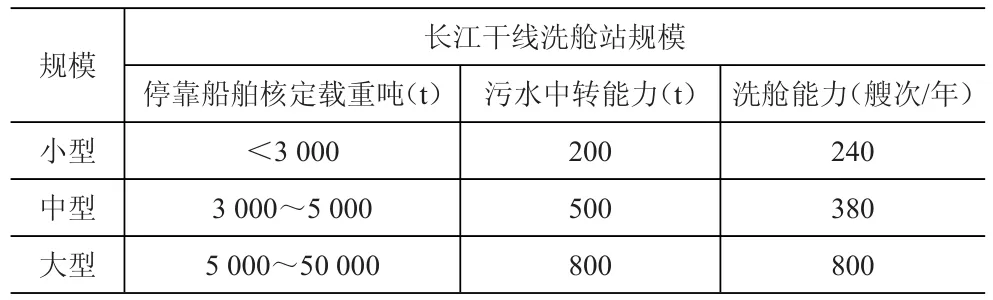
表6 长江干线液化危险品船舶洗舱站规模划分

洗舱站建设要求主要根据水域通航条件、洗舱站可停靠船舶吨级及洗舱能力、后方污水接收及处理能力条件等因素确定，级别越高、规模越大，洗舱站供给能力越强，相应的要求也越高，在选址中考虑的因素也较多。

洗舱站的建设型式有岸基式、趸船式可供选择。岸基式洗舱站普遍适用于各类型船舶的停靠，但无法适应水位差大的区域。趸船式适合全年不同时段水位差别较大地区（如上游库区）。

3.2 洗舱站选址方案

依据洗舱站规模和型式要求，结合已有洗舱站分布情况来“盘活存量”，以未来沿江各省市的船舶洗舱需求量为导向，以沿江主要化工园区为依托，按照前期分散布点、后期逐步加密的方式在干流布点，满足长江干线散装液体危险品船舶运行需求，并对主要支流具有一定的辐射作用。长江干线散装液体危险品船舶洗舱站近远期布局方案见表7。

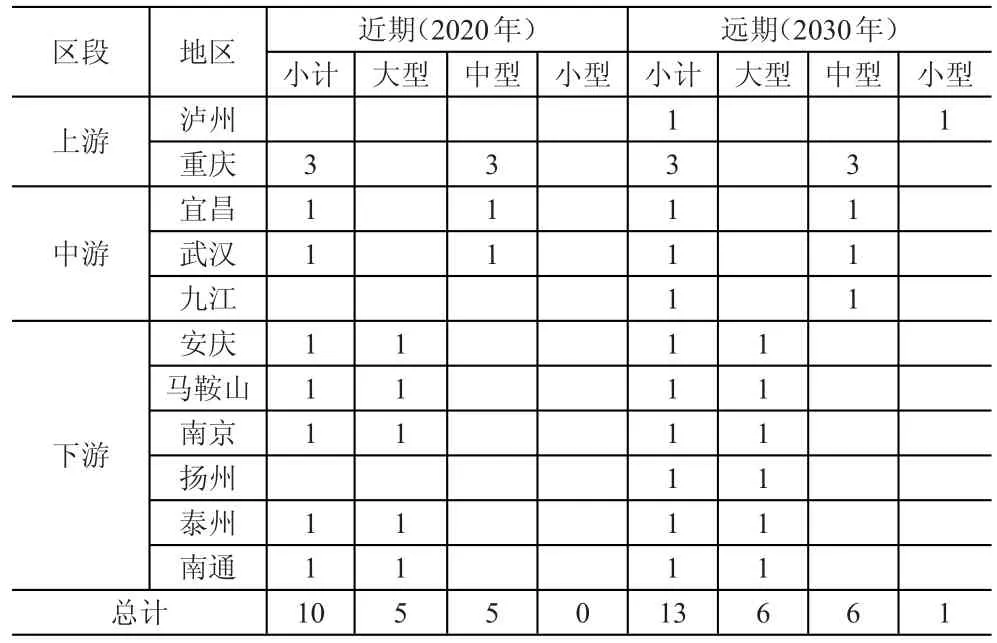
表7 长江干线散装液体危险品船舶洗舱站布局方案（个）

2020年以前，洗舱站相关技术规范尚不完善，此阶段以盘活现有存量，加强管理及加快完善相关技术规范为原则，洗舱站点尽量依托现有洗舱站点进行规划布局，少量新建站点布局在化工园区集聚地，优先满足危险品船舶对洗舱作业的迫切需求。2020-2030年，根据长江干线危险品运输需求增长情况，适当加大站点规模和加密站点。

[1]E T Erdemir,R Batta,S Spielman.Location coverage models with demand originating from nodes and paths：Application to cellular network design[J].European Journal of Operational Research,2008,190：610-632.

[2]E T Erdemir,R Batta.Optimization of aeromedical base locations in New Mexico using a model that considers crash nodes and paths[J].Accident Analysis&Prevention,2008,40：1 105-1 114.

[3]周建勤.面向线状需求的物流节点选址研究[D].北京：北京交通大学,2010.

[4]张其兵.基于集对分析的长江危险品水上运输安全评价研究[D].武汉：武汉理工大学,2013.

[5]贾禹.内河危险化学品运输服务链成本结构分析及优化[D].重庆：重庆交通大学,2013.

[6]李娜.基于状态方程的长江干线水上交通安全评价研究[D].武汉：武汉理工大学,2012.

Study on Location Allocation of Tank-cleaning Station for Transportation Vessels along Yangtze River Main Stream Based on Linear System Concept

Lin Hua1,Li Biaokui1,Xu Peihong2
(1.Wuhan University of Technology,Wuhan 430063;2.Changjiang River Administration of Navigational Affairs,Wuhan 430014,China)

In this paper,based on previous researches,we introduced the concept of the linear system into the zoning of the tankcleaning demand of the 23 major ports along the main stream of the Yangtze River,established the optimal distribution model of the maintenance points for a homogeneous system,then through analyzing and forecasting the fundamental data,solved the model and proposed the location scheme of the tank-cleaning stations for freighters of liquid bulk hazardous cargoes navigating the main stream of the Yangtze River.

linear system;main stream of Yangtze River;bulk liquid hazardous cargo;tank-cleaning station;location allocation

F224.0;U651+.1

A

1005-152X(2017)06-0112-04

10.3969/j.issn.1005-152X.2017.06.026

2017-03-25

林桦（1963-），女，湖北武汉人，副教授，研究方向：港口、航运与综合物流管理、运输经济与政策；李表奎（1990-），男，河南郑州人，硕士研究生，研究方向：港口、航运与综合物流管理。