基于粒子群算法的水火电力系统负荷优化分配

(三峡大学，湖北 宜昌 443000)

1 引言

电力工业是高耗能产业，提高电力工业能源利用效率，转变能源利用方式，减少炭基能源使用量，对于缓解我国能源供需矛盾和改善生态环境等具有重要作用。理论及实践表明，优先利用清洁可再生能源，开展清洁能源与可再生能源的互补运行，是提高电力系统运行经济，提高能源利用效率和可再生能源的有效途径。我国目前火电占的比例为67.3%，火电容量将控制在8.9亿千瓦左右。因此开展清洁能源与常规炭基能源之间联合经济运行的研究具有重要意义。

解决此问题的研究方法有传统的经典算法和智能算法。传统的经典算法又以动态规划规划算法及其改进为代表，如离散微分动态规划算法，逐次逼近动态规划算法，增量动态规划算法，逐步优化算法等。智能算法有遗传算法及其改进，粒子群算法，差分进化算法及其改进。

早由Howson和Sancho于1975年提出，它是在动态规划的思想上，运用最优化原理求解多状态的动态规划。它是每两个阶段的决策相对其始端决策和终端决策是最优的。POA法应用于水库群的优化调度问题时[1]，可以先将水库群分成多个单水库系统，对每一个水库进行优化，以此作为整个水库群优化问题的最初解，然后再考虑水库群联合运行，逐步改进优化策略，如果对于梯级水库群，也可以把梯级水库群作为一个整体，在两阶段里自上而下逐一寻优；如果是混联系统，寻优应从调节最不好的小水库开始。当然，除了POA算法较好的全局收敛性，计算易实现以外，算法对初值的依赖性是它的缺点，不同的初值对于迭代次数，计算速度都有十分重要的影响。

粒子群算法是由Eberhart和Kennedy于1995年提出的一种模仿鸟群寻找食物的随机搜索算法。从本质上讲，粒子群算法是一种群体智能的进化算法，它以粒子的位置(优化问题的解)为运算对象，使各粒子不断以自身最好位置(个体最好解)和种群最好位置为引导，调整飞行速度和方向，并在迭代飞行中更新个体最好解和全局最好解，最终逼近全局最优解。

与传统算法相比，简单遗传算法更容易求解高维水库的优化调度问题，但其编码的设计导致了算法的搜索效率较低。

粒子群算法是由Eberhart和Kennedy于1995年提出的一种模仿鸟群寻找食物的随机搜索算法。从本质上讲，粒子群算法是一种群体智能的进化算法，它以粒子的位置(优化问题的解)为运算对象，使各粒子不断以自身最好位置(个体最好解)和种群最好位置为引导，调整飞行速度和方向，并在迭代飞行中更新个体最好解和全局最好解，最终逼近全局最优解。

2 建立模型

水火电站的问题关键在于最小化火电厂的煤耗成本，同时利用水力资源尽可能的多。目标函数与相关的约束如下：

负荷平衡约束：

梯级水电站的水量:

Vm,t+1=Vm,t+Im,t-Qm,t-Sm,t+Qm,t(t-τi-1)+Sm,t(t-τi-1)

水电转换关系:

水库需水量约束:

水电站的发电引用流量约束:

水电机组的出力约束:

火电机组的出来约束

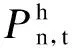
3 粒子群算法

粒子群算法(pso)是在1995年被提出的一种启发式算法。PSO模擬鳥群的捕食行為。设想这样一个场景：一群鸟在随机搜索食物。在这个区域里只有一块食物。所有的鸟都不知道食物在哪里。但是他們知道当前的位置离食物还有多远。最简单有效的方法就是搜寻目前距离食物最近的鸟的周围区域。PSO从这种模型中得到启示并用于解決优化问题。PSO中，每个优化问题的解都是搜索空间中的一只鸟。我们称之为"粒子”。所有的粒子都有一个由被优化的函数決定的适应值，每个粒子还有一个速度決定他們飞翔的方向和距离。然后粒子們就追随当前的最优粒子在解空間中搜索，具体来说，PSO初始化为一群随机的粒子(随机解)，然后通过迭代找到最优解，在每一次迭代中，粒子通过跟踪两个“极值”来更新自己。第一个就是粒子本身所找到的最优解，这个解叫做个体极值pBest,另一个极值是整个种群目前找到的最优解，这个极值是全局极值gBest。

4 算例

为了求解出更好的优化结果，取自文献[6]的测试系统被使用。系统由一个火电站和四个沿河而建的水电站组成，如图1水力系统测试网络。调配周期为1天，时间间隔为1个小时。用于本测试网络的细节数据在表1～3中给出。表1是1天的用户的负荷需求。表2是各水电站的发电系数。表3是水库库容，发电流量的范围。四个水电站的每小时的来水径流分别是[10000 8000 1000 0],水流传输的延迟时间分别是，目标函数的系数分别是1000,10,0.5。

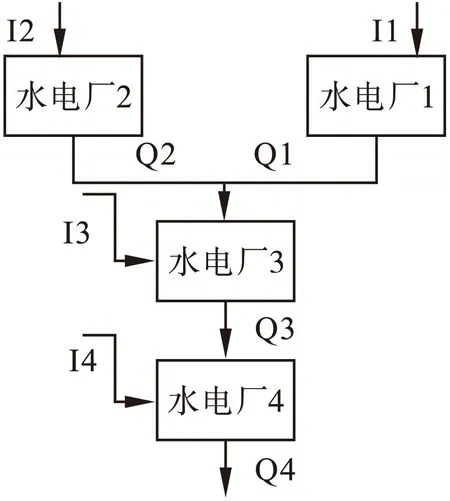
图1

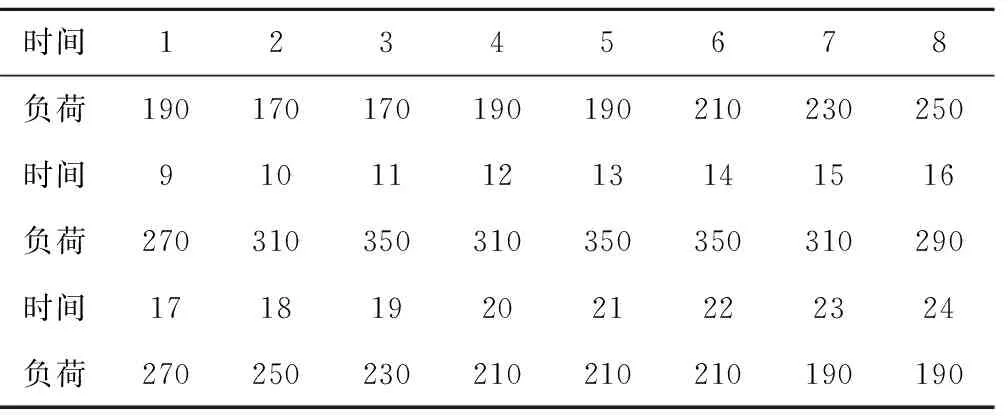
时间12345678负荷190170170190190210230250时间910111213141516负荷270310350310350350310290时间1718192021222324负荷270250230210210210190190

表2

表3

5 结论

表4是用粒子群算法计算的4个水电站和1个火电站的发电量的结果。粒子群算法结果比较好，火电厂的最小秏煤量是154338.1。

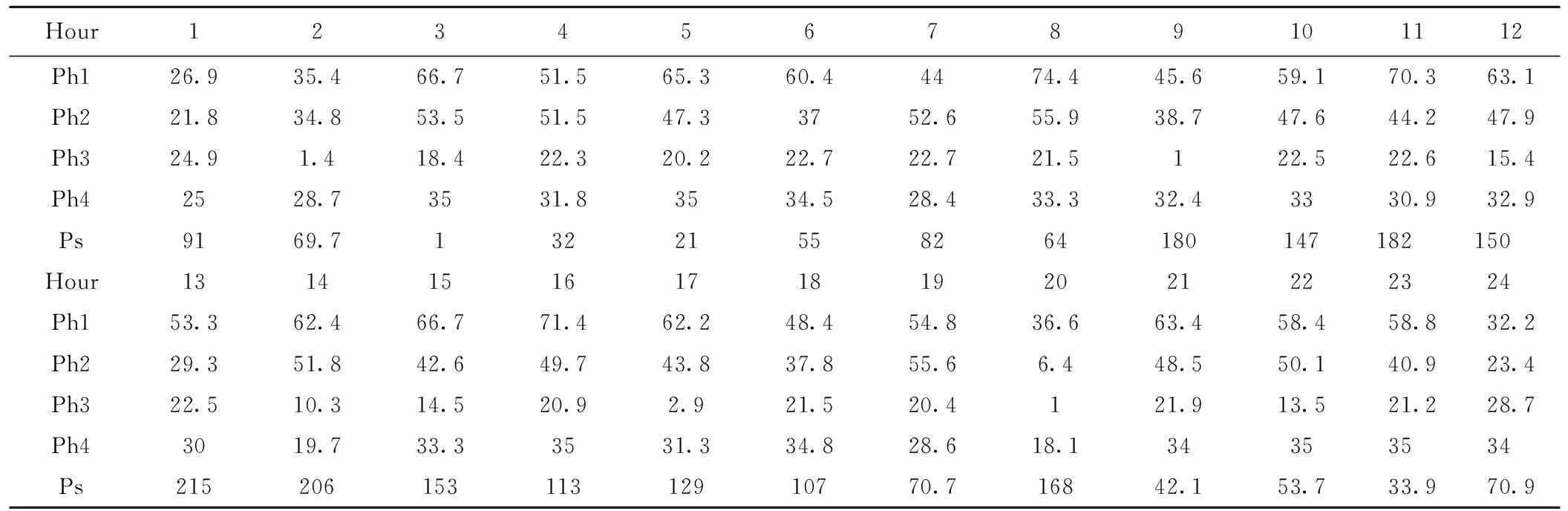
表4

[1] 侯贸军,罗春辉,隗霖捷,等.基于微分进化算法的水火电短期优化调度的研究[J].电力系统保护与控制,2015(9)63-70.

[2] Yang J,Chen N.Short-term hydrothermal coordination using multipass dynamic programming.IEEE Trans Power Syst,1989,4(3):1050-1056.

[3] Tang J,Peter B.Hydrothermal scheduling via extended differential dynamic programming and mixed coordination.IEEE Trans Power Syst,1995,10(4):2021-2028.

[4] Turgeon A.Optimal short-term hydro scheduling from the principle of progressive optimality.Water Resour Res,1981,17(3):481-486.

[5] 张景瑞，龙健，岳超群,等.水火电力系统短期优化调度的一种改进粒子群算法[J].控制与决策,2011(3):89-94.

[6] Naresh R,Sharma J.Two-phase neural network based solution technique for short term hydrothermal scheduling.IEE Proc Gener Transm Distrib,1999,146(6):657-663.