水电站机组组合的最优动力特性研究

，，

(三峡大学电气与新能源学院，湖北 宜昌 443000)

1 引言

能源是国民经济发展的基础，是社会稳步发展的前提。为了社会的持续发展，能源问题已经成为了人类社会发展的关键点，也是大家关注的焦点。

水电站厂内经济运行是在满足电能生产的安全、可靠、优质的前提下，合理的组织调度电厂的发电生产设备，以期获得尽可能大的经济效益[1]。随着我国水电站建设的飞速发展，水电在电力系统中所占的比重越来越大，截止2014年底水电总装机容量已突破3亿千瓦，占全国发电总量的27%。水电事业的快速发展，水电站规模的扩大、机组的增多，装机容量的增大使得水电站经济运行研究越来越必要，由于大规模水电机组的发电量基数是非常庞大的，若发电量提高一个百分点左右，就可以带来相当可观的经济效益。

水电站最优动力特性曲线指水电站所有可带负荷的最优运行曲线，包括了水电站所有可带负荷的最优发电流量及水电站厂内最优经济分配。提高电力系统的动能经济效益一定程度上决定于系统中水电站的运行工况最优化。为此，必须对水电站动力特性资料，特性曲线，最优工作机组台数和组合，机组的合理启动与停止以及在各运行机组间有功的最优分配等方面作深入的研究，方能得到水电厂内最优运行方式，用以指导水电厂的实际运行，以获得电站运行的最大效益。水电站最优动力特性曲线集中反映了上述成果，用它指导水电站实现厂内最优运行十分方便。水电站厂内经济运行一般指在总负荷给定的条件下确定其厂内工作机组最优台数、组合及启停次序，机组间负荷的最优分配，以提高水电站运行时的经济效益。

2 模型建立

2.1 目标函数

式中：Q—梯级龙头水库的日发电流量(m3/s)；

Q1t—水库在第t时段的发电流量(m3/s)；

η1t—水库在第t时段的水轮机综合效率；

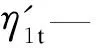
2.2 约束条件

出力平衡约束：

机组出力限制约束：

Nimin≤Ni≤Nimax

机组出力禁区约束：

Ni∈[N0min,N0max]

水量平衡约束：

Vt,j=Vt-1,j+(αjqt-τj,j-1+ΔIt,j-qt,j-nt,j)Δt

机组引用流量约束：

qimin≤qi,t≤qimax

水库库容约束：

Vt,jmin≤Vt,j≤Vt,jmax

水流联系：

It,j=αjqt-τj,t-1+ΔIt,j

边界条件：

其中：

Ni,t(qi,t,Hi,t,ηi,t)—为t时段第i台机组的出力；

Ni—t时段整个梯级子系统的负荷；

It,j—第j级电站t时段的入库流量；

qt,j—第j级电站t时段的入库流量；

τj—流达时间，即(j-1)级水库的出库水流流达j级水库入库的时间，j≥1；

ΔIt,j—(j-1)级水库与j级水库间在t时段的区间入库流量，j≥1；

αj—坦化系数，其大小与上游水电厂至下游水库距离有关；

nt,j—第j级电站t时段的非发电用水流量；

j—梯级水电站中水电站的数目，j=1,2,3,…M；

i—梯级水电站中机组的台数，i=1,2,3,…N；

Vt,j—j级水库t计算时段末的水库容量；

ZO,j,ZE,j—j级水库t计算时段末的水库容量；

Δt—计算时间间隔(1小时)；

N0min,N0max—分别为各机组的出力禁区的下限、上限；

3 算法讲解

3.1 惩罚函数法

惩罚函数法是求解约束优化问题的一种有效方法，其将约束优化问题中的约束违反度乘以惩罚项加到目标函数中，从而构造出带参数的增广目标函数。这种构造的主要思想是把一系列的约束优化问题转化为无约束的优化问题进行求解。在增广目标函数中，惩罚因子的不断变化，导致最优解也不断变化，最终趋于原问题的最优解。由于惩罚函数每一迭代步不涉及可行方向的计算法，因此更适合非线性约束优化问题的求解。

现在惩罚函数法一般具有两种形式：外点惩罚法和内点惩罚法。外点惩罚法的搜索是从不可行域到可行域。而内点惩罚法是从可行域中进行搜索，惩罚项的大小和解与约束边界的距离成反比关系，当解接近约束边界时，惩罚项将趋于无穷大。这样，可行域的边界如同一道不可逾越的墙，将内点惩罚函数的极小值点限制在可行域的内部，从而失去不可行域中有价值的信息。内点惩罚法最大的不足是初始种群中要有一个可行解，而对于某些问题而言，找到可行解本身就是一个问题[2]。

在实际运算中，惩罚项太大或太小都会影响最终的结果。

3.1.1 内点法

内点法的特点是将构造的新的无约束目标函数——障碍函数定义在可行域内，并在可行域内求惩罚函数的极值点，即求解无约束问题时的探索点总是在可行域内部，这样，在求解内点惩罚函数的序列无约束优化问题的过程中，所求得的系列无约束优化问题的解总是可行解，从而在可行域内部逐步逼近原约束优化问题的最优解。

内点法是求解不等式约束问题的一种行之有效的方法，但不能处理等式约束。因为构造的内点惩罚函数是定义在可行域内的函数，而等式约束优化问题不存在可行域空间，因此，内点法不能用来求解等式约束优化问题。

内点法构造方法：

对于数学模型：

minf(X)

gi(X)≥0

令k=1,ε=0.0001,r1=1,c=0.1并给定可行的初始解X(0)。

第一步：构造障碍函数：

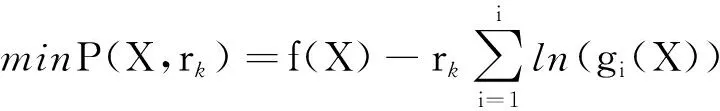
第二步：求解无约束非线性优化问题：得到了一组最优解X(k)。

(本例中，运用的是共轭梯度法求解)

第三步：验证解的收敛性。

‖X(k)-X(k-1)‖<ε或|f(X(k))-f(X(k-1))|<ε

若成立则所得解X(k)最优，否则令r(k+1)=cr(k)，且X(0)=X(k)重复第一步的迭代。

其中：r(k)—第k次迭代中的障碍因子;

c—降低系数

注意的几个问题：

(1)初始点的选择：①在可行域内②不要离边界太近。

(2)障碍因子初值的选择：不要太大，也不能太小。

(3)降低系数的选择：一般在0.1～0.7之间。

评价：用于目标函数比较复杂，或可行域外无定义时，求解过程中的所有过程量都是可行的解，但是，内点法不能解决等式约束且初值的选择也会影响最后结果。

3.1.2 外点法

外点法是一种将新的目标函数构建在可行域外，然后随着惩罚因子的递增，生成一系列的新目标函数。外点法可以解决含有等式约束的非线性优化问题。

对于数学模型：

minf(X)

gj(X)≥0

hi(X)=0

令k=1,ε=0.0001,M1=1,a=10并给定不可行的初始解X(0)。

第一步，构造惩罚函数。

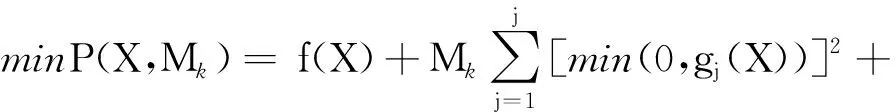
第二步：求解无约束非线性优化问题：得到了一组最优解X(k)。

(本例中运用的是共轭梯度法求解)

第三步：判断是否在边界外。

对任意的j，都有-gj(X(k))<ε迭代停止，最优解为X(k)，否则下一步。

第四步：验证解的收敛性。

‖X(k)-X(k-1)‖<ε或|f(X(k))-f(X(k-1))|<ε

若成立则所得解X(k)最优，否则令M(k+1)=aM(k)，且X(0)=X(k)重复第一步的迭代。

注意的几个问题：

(1)初始点的选择：基本上是可以随意选择;

(2)惩罚因子初值的选择：不要太大，也不能太小;

(3)递增系数的选择：一般在5～10之间;

(4)求解工程中的所有过程量都是不可行的。

3.1.3 混合惩罚函数法

对比上述两种方法，不难看出，外点法和内点法的区别主要就是初始点的选择和过程量是否在可行域。根据这个特点，我们可以很好得分辨出两种算法的应用范围。

内点法适合应用于初始点易找或者在已有的某种结果上进行改进。而外点法则更适用于约束条件复杂，可行点难以寻找的问题。由于外点法只有最终迭代的结果是可行解，所以对于一些工程问题可能对过程量有要求的内点法也更加合适。

因此，综合两种方法的特点，拟采用内点法解决约束范围内的约束，用外点法解决约束范围外的约束及等式约束。

对于数学模型：

minf(X)

gj(X)≥0

hi(X)=0

构造惩罚函数：

运算过程和外点法基本一样。

3.2 共轭梯度法

对于无约束非线性优化模型：

minf(X)

令k=0,ε=0.0001并给定可行的初始解X(0)并计算f(X(0))，令P(0)=-f(X(0))

第一步：计算步长。

采用(海塞矩阵的方法)：

第一次迭代计算：X(k+1)=X(k)+λkP(k)

第二步：验证收敛性。

第三步：确定迭代方向：

P(k+1)=-f(X(k+1))+βkP(k),

重复第一步的迭代计算。

整体流程图如图1所示。

图1 惩罚函数法流程图

4 实例分析

对于某水电站，其中有4台机组，其运行特性如下表所示，运用上述惩罚函数法，可以得到如下结果。

表1 机组特性数据

从图中看出各个机组的分配采用一种梯度的分配方式，当需要负荷达到100WM时，第2台机组投入运行，当负荷到达200WM时，第3台机组投入运行，当负荷达到287WM时，第4台机组投入运行。然而从图中还不能完全看出各个机组具体分配方式，因为线段重合看不清楚后续的分配方式，因此得到下列4张图分别表示各个机组的分配方式看起来更加清晰。

[1] 李文沅.电力系统安全经济运行-模型与方法[M].重庆大学出版社,1989.

[2] 卢永忠.梯级水电站的优化调度研究[J].重庆大学,2007.

[3] 覃晖,周建中,肖舸,等.梯级水电站多目标发电优化调度[J].水科学进展,2010,3:377-384.

[4] 胡国强.梯级水电站优化调度模型与算法研究[D].华北电力大学(北京),2007.

[5] 吴杰康,郭壮志,丁国强.采用梯级水电站动态弃水策略的多目标短期优化调度[J].中国电机工程学报,2011,4:15-23.

[6] 吴杰康,朱建全.机会约束规划下的梯级水电站短期优化调度策略[J].中国电机工程学报,2008,13:41-46.

[7] 徐刚,马光文.基于蚁群算法的梯级水电站群优化调度[J].水力发电学报,2005,5:7-10.

[8] 王铮.梯级水电站群联合优化调度及其决策方法[D].华北电力大学,2014.

[9] 段云辉.小型梯级水电站优化调度运行研究[D].郑州大学,2014.

[10] 欧阳俊,袁中祥,郑丹,等.基于改进粒子群算法的梯级水电站优化调度[J].陕西电力,2013,1:48-51+56.

[11] 朱敏,王定一.电力系统中梯级水电站实时优化运行控制新算法[J].电力系统自动化,1997,4:33-36.