利用应变片测量金属弹性模量

高志华 魏江兵 张 涔 贾 艳

(1东北师范大学物理学院，吉林 长春 130024;2建水一中，云南 建水县 654399)

利用应变片测量金属弹性模量

高志华1魏江兵2张 涔1贾 艳1

(1东北师范大学物理学院，吉林 长春 130024;2建水一中，云南 建水县 654399)

本文给出了金属弯梁的应变与其负载质量的关系及利用应变片和惠斯通单臂电桥中的电流测量金属弹性模量的公式；对利用应变片直接测量应变的方法和利用光杠杆测量驰垂度的方法测量铜棒弹性模量的实验结果进行了比较；讨论了利用应变片直接测量梁的应变的方式测量金属弹性模量的影响因素。 本文研究表明：理论上利用应变片和单臂电桥电流可以测量梁的弹性模量；利用应变片和单臂电桥测量物体弹性模量与光杠杆方法的测量结果相差1%，此法测量的准确性好；单臂电桥的灵敏度低且缺少温度补偿功能可使测量结果波动，导致6组测量结果与平均值的最大差异为2.6%，通过对多组测量求平均值，可在很大程度上降低上述因素引起的测量误差。

弹性模量 应变片 惠斯通电桥 光杠杆 梁弯曲法

弹性模量是工程技术设计中常用的参数，对研究金属材料、光纤材料、半导体、纳米材料、聚合物、陶瓷、橡胶等各种材料的力学性质有着重要意义。测量弹性模量的方法主要有：静态测量法、共振测量方法、弹性波波速测量法及泊松比测量法等[1]，其中静态测量法是实验教材普遍采用的测量方法，包括静态拉伸和静态弯曲方法，测量的主要工作为测量样品拉伸和弯曲的微小形变。人们利用声、光、电等测量微小形变技术，发展了光杠杆、霍尔器件[2]、涡电流[3]、电感、电容、巨磁电阻[4]、光纤位移传感器、衍射、干涉[5]、莫尔条纹、超声波等多种测量物体弹性模量的技术。在梁弯曲法中，目前研究主要集中在改进驰垂度的测量方法上[6]，缺少梁的应变与弹性模量关系的相关理论和对直接测量应变实验方法的研究。 本文推导了梁的应变与梁的弹性模量的关系，利用应变片直接测量梁的应变的方法测量了铜棒的弹性模量并对利用应变片测量梁的弹性模量的影响因素进行了分析总结。

1 梁弯曲法测量弹性模量原理

1.1 金属棒弹性模量与应变片应变关系

当在金属棒中点挂质量为m的砝码时，金属棒弯曲，棒的中间层以下为拉伸状态，中间层以上为压缩状态，其纵断面如图1所示。在中间层取距离为dx的两横断面Q1、Q2，棒弯曲前互相平行，弯曲后成一小角度dφ。距离中间层为y、厚dy、变形前长为dx的一小段，弯曲后伸长了ydφ，它受到的拉力为dF，根据胡克定律有

图1 梁弯曲应力示意图

式中dS表示变形层的横截面积，即dS=bdy。于是

(1)

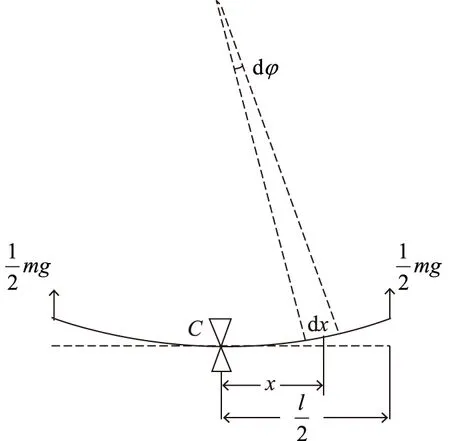
图2 梁弯曲等效示意图

故有

(2)

根据dl=ydφ可得棒下表面长度为dx的一段产生的伸长为

设应变片的长度为l′，则应变片的总伸长量为

应变片的应变为

(3)

1.2 利用单臂直流电桥的电流测量金属棒弹性模量原理

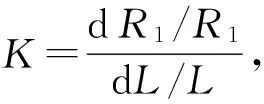
(4)

由式(3)、(4)可得，

见图3，将检流计接入BD之间，电阻箱接入R1所在臂，改变电阻箱的阻值，对电桥进行定标得到I—ΔR1关系曲线的斜率，于是铜棒的弹性模量为

(5)

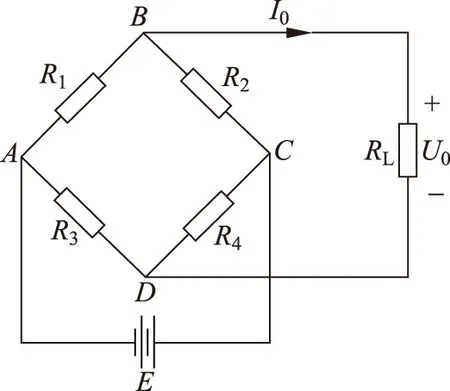
图3 单臂直流电桥

式(5)对应的弹性模量不确定度计算公式为

(6)

1.3 利用光杠杆测量梁的弹性模量原理

采用光杠杆法测量杨氏模量光路如图4所示，当光杠杆前脚a下降δ时，镜面M1偏转角度为θ，入射到望远镜中的反射光线的偏转角为2θ，望远镜中看到尺的位置变化为|x2-x1|，对光杠杆前脚的微小位移δ起到了放大作用。

图4 光杠杆放大原理示意图

利用光杠杆测量金属横梁弹性模量理论为[8]

(7)

式中，δ为铜棒厚度；b为金属棒宽度；l为的支架两刀口间距；d1为光杠杆前足尖到两后足尖的垂直距离；d2为光杠杆平面镜到望远镜直尺水平距离；k为望远镜读数变化随悬挂砝码质量变化曲线的斜率。

其不确定度计算公式为

(8)

本文的数据处理采用最小二乘拟合方式，其斜率对应的标准差为

(9)

式中，b为拟合直线斜率；r为拟合相关系数；n为测量次数。

2 实验测量结果及分析

2.1 待测铜棒的尺寸

实验分别使用游标卡尺和螺旋测微计测量了铜棒5个不同位置的宽度和厚度，游标卡尺精度为0.02mm，测量结果如表1所示。由于铜棒的两支撑刀口间距有标称值，故用米尺对其进行一次性测量：l=(40.00±0.02)cm。

表1 待测铜棒的宽度和厚度

2.2 光杠杆法测量铜棒的弹性模量

由于影响光杠杆法测量的弹性模量的因素比较明确可控，因此，本文利用光杠杆法测量的铜棒的弹性模量，以考察使用应变片测量的准确性。 实验中望远镜和光杠杆距离保持足够远，在望远镜里面看到尺的位置与望远镜镜筒等高；读数时保持视线高度不变。

实验用钢直尺测量光杠杆的前、后足尖间距：d1=(4.45±0.01)cm，光杠杆平面镜到望远镜直尺的水平距离为：d2=(217.30±0.04)cm。

利用式(9)可得k=(0.0347±0.0002)g·cm, 由式(8)得铜棒弹性模量为Y=(10.35±0.03)×1010N·m-2。由表2可见，悬挂相同质量的砝码，增加、减少砝码过程尺度望远镜的尺读数差别小，单次测量数据的相关性好，弹性模量的结果稳定，相对平均值的最大偏离是0.06%，精确度比较高，因此，可作为标准评价其他测量方法的测量结果。

2.3 利用应变片测量铜棒弹性模量

实验使用应变片的标示参数为：静态阻值R=120.0Ω，灵敏度k=2。 惠斯通电桥的4个臂的电阻相同，即：R1=R2=R3=R4=120.0Ω，.R1所在臂定标时接入电阻箱，测量时接入应变片。 将应变片平行贴在棒的下表面中间，关于棒长、宽均为对称，静置24小时后进行测量。 实验使用DF1730SBSA型直流电源，输出电压设为E=7.0V；选用AC15-A型直流检流计，档位选择10nA档，最小分度为0.2nA。电桥定标数据及结果如表3和图5所示。

利用式(9)可得k1=(143.08±0.87)nA·Ω-1。 表3表明，各组定标数据的线性关系都比较好，但是不同组测量的结果有波动，采用测量电流平均值进行定标计算的结果线性关系与单次的相比没有明显提高。相比于测量数据平均值定标的结果，两组定标线的斜率的偏差为0.6%，这种差异主要来源于电阻箱旋钮的接触电阻的影响。 因此，采用增、减R1两个过程的平均值进行定标更加合理。图5表明，电阻变化与检流计电流有很好的线性关系。

实验利用应变片对铜棒的弹性模量进行了6组测量，砝码从0g砝码增加到350g，每次增加50g，然后再依次将砝码减少至0g。取k1=(143.08±0.87)nA·Ω-1计算铜棒弹性模量，测量数据及弹性模量计算结果如表4所示。

利用测量数据平均值，根据式(9)得k2=(71.52±0.38)×10-3nA·g-1，根据式(6)得弹性模量为Y=(10.26×1010±0.09)N·m-2，相比于利用光杠杆测得结果相差1%，表明应变片在梁弯曲法弹性模量测量实验中可得到与使用光杠杆进行测量精度相当。 表4中6组测量数据的弹性模量存在不同程度的差异，相比于取平均的弹性模量最大偏离为2.6%，这反映了使用应变片测量结果存在波动性。 在加砝码和减砝码两个过程中对应相同的砝码质量，检流计读数差异较大，加砝码过程测得弹性模量普遍小于减砝码的结果，反映了测量结果离散性和不稳定性。 实验还表明利用多组测量取平均的方法，可以使减少单次测量产生的随机误差，保证测量结果的准确性。

与杠杆法测量方法相比，使用应变片测量时的不稳定性主要是由于应变片粘贴和使用方法引起的。一方面，应变片本身的横向效应、端部应力集中、胶黏剂的蠕变引起灵敏度降低[7]；更重要的是测量电流采用单臂电桥灵敏度低[9]且没有温度补偿功能，随着时间推移，应变片温度升高、电阻增加，在加砝码过程中使电流变化偏大，弹性模量减小，在减砝码过程中检流计电流变化偏小，使弹性模量增大；此外，使用灵敏检流计的分度值为

表2 光杠杆法测量弹性模量数据及结果

表3 电桥电流定标数据

注：I1：检流计电流；Ia：对两组电流求平均；“加、减”：分别表示增加和减少R1电阻，k1、r分别为定标线的斜率和相关系数。

表4 应变片测量铜棒弹性模量数据及结果

注：I1：检流计电流；Ia：对6组电流的平均值，“加、减”：分别表示增加和减少砝码。

0.2nA，50g砝码引起的电流变化在0.7nA左右，因此，检流计分辨率相对偏低，导致测量结果不准确，若取读数误差为0.05nA，以平均后的数据计算k2的相对误差大于1%。 根据式(6)各测量值及相应不确定度可知，弹性模量不确定度主要来自k1、k2的不确定度，因此，电桥的灵敏度和温度补偿及检流计精度对当前测量结果的准确性影响很大。实验表明对多组测量取平均可减少电桥本身因素引起的影响；增加砝码数量可增加检流计电流变化范围，减小因检流计分辨率引起的误差，使测量结果更准确。

3 总结

本文推导了利用弯曲法测量金属弹性模量时，梁的下表面应变与负载质量及单臂电桥电流之间的关系；通过对单臂直流电桥的电流进行定标的方式测量了铜棒的弹性模量，结果与光杠杆法相比相对误差为1%，表明利用应变片测量金属弹性模量是可行的。实验结果表明：在利用应变片测量物体弹性模量时，应变片缺少温度补偿措施会导致增加砝码和减少砝码过程中弹性模量偏大或偏小；电桥放大倍数低、检流计的精度不高会严重影响测量结果的准确性，二者协调选择可使测量更准确；进行多组测量取平均可在很大程度上减少上述因素造成的影响，得到比较准确的结果。 本文将应变片的使用和弹性模量的测量相结合，为应变片的使用和弹性模量的测量提供了新的参考。鉴于应变片的粘贴方法简单和惠斯通电桥在实验室中容易实现等特点，适合将本文实验开设为本科生设计性实验。通过本实验可使学生深刻理解应变片的工作原理和使用方法，提高学生动手能力、分析问题和解决问题能力。

[1] 中国金属学会，中国有色金属学会，金属材料物理性能手册(第一册)金属物理性能及测试方法[S].北京：冶金工业出版社，1987.

[2] 沈元华，陆申龙.基础物理实验[M].北京：高等教育出版社,2003:96-99.

[3] 顾纯学，王士英.用电涡流传感器测金属丝杨氏模量[J].大学物理,1999(04):25-28. Gu Chunxue， Wang Shiying. Measurement of Young’s modulus of metal wire by eddy current sensor[J]. College Physics, 1999， (04)： 25-28． (in Chinese)

[4] 梁志强，庄明伟，韩立铭,等.基于巨磁电阻效应的杨氏模量测量装置[J].大学物理,2014(02):45-48. Liang Zhiqiang， Zhuang Mingwei， Han Liming， et al. A device of measuring Young’s modulus based on giant magnetoresistance effect[J]. College Physics， 2014， (02)： 45-48. (in Chinese)

[5] 方运良，崔娟，朱伟玲.双缝干涉法测量金属的杨氏模量[J].物理实验.2014(01):37-39. Fang Yunliang， Cui Juan， Zhu Weiling. Measurement of Young’s modulus of metal with two-slit interference method[J]. Physics Experimentation， 2014， (01)： 37-39. (in Chinese)[6] 梁霄，田源，铁位金,等.横梁弯曲衍射法测杨氏模量实验仪的研制[J].物理实验，2011(08):31-33. Liang Xiao, Tian Yuan， Tie Weijin， et al. Developing a device for Young’s modulus measurement with bent beam and light diffraction[J]. Physics Experimentation， 2011， (08)： 31-33. (in Chinese)

[7] 尹福炎.电阻应变片与应变传递原理研究[J].科技应用，2010(2):1-8. Yin Fuyan， Study on the principle of resistance strain gauge and strain transfer[J]. Applied Science and Technology， 2010(2)： 1-8. (in Chinese)

[8] 杨述武，普通物理实验(一、力学及热学部分)[M].北京:高等教育出版社,2005:92-96.

[9] 吴祥晨，吴炀杰，王柳烟.电阻应变片测量电路的灵敏度研究与误差分析[J].电子制作，2014(03):51. Wu Xiangchen， Wu Yangjie， Wang Liuyan. Study on the sensitivity and error of resistance strain gauges circuit[J]. Practical Electronics. 2014， (03)： 51. (in Chinese)

MEASUREMENT OF METAL ELASTICITY MODULUS BY STRAIN GAGE

Gao Zhihua1Wei Jiangbing2Zhang Cen1JiaYan1

(1School of Physics, Northeast Normal University, Changchun Jilin 130024；2Jianshui 1st High School, Jianshui Yunnan 654399)

The relation between tensile strain and the weight load of a bending copper beam and the formula of testing elasticity modulus with a strain gage and current in single-arm Wheatstone bridge were derived in this paper. The elasticity modulus of the copper beam were measured by the strain gage directly and by the optical lever method indirectly. The results were compared and some influence factors were discussed based on the direct measuring method. Studies in this paper show that both of the two methods are effective. There was only 1% difference between the experimental results by using two different methods. However, the accuracy of measurement is better in the direct method by the strain gage. In the indirect method, the lower sensibility and the lacking of temperature compensation of single-arm Wheatstone Bridge were proved to be major factors that lead to errors produced in this paper, where the biggest difference from the average value can be 2.6%. Increasing test times was an effective way to reduce the bias of the results.

elasticity modulus; strain gage; Wheatstone bridge; optical lever; bending beam test method

2015-09-20；

2015-11-09

东北师范大学教师发展项目15B2XZJ001。

高志华，女，讲师，主要从事物理教学科研工作，研究方向为理论模拟计算，gaozh142@nenu.edu.cn。

高志华，魏江兵，张涔，等. 利用应变片测量金属弹性模量[J]. 物理与工程，2017，27(2)：37-41,46.