以乒乓球为例分析旋转球的受力及飞行轨迹

赵丽特 范东华 陈毅湛

(五邑大学应用物理与材料学院，广东 江门 529020)

以乒乓球为例分析旋转球的受力及飞行轨迹

赵丽特 范东华 陈毅湛

(五邑大学应用物理与材料学院，广东 江门 529020)

文章对体育运动中一些有趣的物理现象进行探讨，有助于提升学生学习物理的兴趣。文章利用基本的力学定律对乒乓球的6种基本旋转和飞行轨迹进行了详细的分析,讨论了初速度对飞行曲线的影响；进而对其他球类运动中的有趣现象进行了讨论，比如“蛇球”(“香蕉球”)以侧旋为主，“消失的发球”以逆旋为主，“电梯球”以上旋为主，“零式发球”以下旋为主；并对1997年罗伯特卡洛斯的经典香蕉任意球进行了计算，给出了该球水平方向最大偏移距离和旋转角速度的定量结果。

乒乓球；旋转；香蕉球；蛇球；电梯球；零式发球；消失的发球；马格努斯力

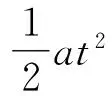
与足球、网球、排球等相比，乒乓球的旋转种类繁多，所以本文以乒乓球为例，对其6种基本旋转和飞行轨迹进行了详细的分析，进而对其他球类运动中的有趣现象进行了讨论，比如引人关注的“香蕉球”“蛇球”“电梯球”“零式发球”“消失的发球”等，并对1997年罗伯特·卡洛斯的经典香蕉任意球进行了计算。

1 各种旋转球的特性分析

虽然乒乓球可以产生多种多样的旋转，会有各式各样的旋转轴，但是，它始终是围绕3条基本转轴及6种基本旋转而变化的[4]。以图1击球者的方位看(文中其他关于向左、向右等方向的描述均以相应图示的击球者所站方位看)，通过球心与台面相垂直的轴为上下轴(竖轴)，俯视时，球绕轴逆时针旋转为右侧旋球，顺时针旋转为左侧旋球；通过球心与击球线路相垂直的轴为左右轴(横轴)，从左向右看，逆时针旋转为上旋球，顺时针旋转为下旋球；通过球心和击球线路相平行的轴为前后轴(纵轴)，从后往前看，逆时针旋转为逆旋球，顺时针旋转为顺旋球。

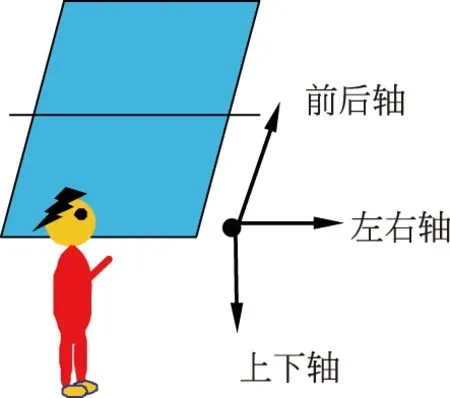
图1 乒乓球的3条基本转轴

乒乓球运动过程中的受力主要来自与球拍或球台的触碰过程以及飞行过程。乒乓球飞出的角度随来球速度、接球角度及受力情况等因素变化，下面讨论发球者的球拍对球的撞击力为前后轴方向，挡球者沿来球方向平挡时乒乓球的运动情况。

1.1 侧旋球

发左侧旋球，球拍从球的后面给球向左的摩擦力必不可少，根据质心运动定理，初速度对发球者来说一定偏左。球在飞行期间，球的左沿气流与迎面气流方向相反，流速减慢，右沿气流和迎面气流方向相同，其流速加快。根据伯努利方程，流速越慢，压强越大；流速越快，压强越小。球的左沿空气压强大，右沿空气压强小，空气给球一个向右的空气压力，这种横向的力也称为马格努斯力[5]。忽略重力作用，以初速度向左飞出的乒乓球，在飞行中受到方向恒向右的力，这与斜向上抛手榴弹，飞行中只受到向下重力作用相似，类比斜上抛运动的轨迹，左侧旋球在球台上的飞行轨迹投影为顺时针飞行弧线。同理，右侧旋球初速度偏右，在飞行中受到方向恒向左的马格努斯力，飞行轨迹在球台上的投影为逆时针飞行弧线。侧旋球水平方向的飞行弧线及受力分析如图2所示。

图2 侧旋乒乓球受力分析及飞行弧线俯视图

从上面的分析中，可以发现马格努斯力并不是轨迹产生“初始偏移”的原因，比如右侧旋球从右方飞出，是因为初速度有向右的分量，所以初速度才是产生“初始偏移”的原因。马格努斯力方向向左，反而是使之“回旋”的原因。

网球中2013法网费德勒击出“回旋蛇球”，球从球场外绕回对方场地内；足球中的“香蕉球”，球绕过人墙眼看要飞出场外又拐回来直扑球门，原理都与侧旋乒乓球一样。

平挡左侧旋球，球给拍面一个向右的摩擦力，拍面给球体大小相等、方向相反的摩擦反作用力，球向左方反弹。右侧旋球反之，触拍后球向右方反弹。

1.2 顺、逆旋球

要产生顺旋球，拍面要从球的下面给球一个向左的摩擦力，根据质心运动定理，顺旋球的初速度会偏左，同理，逆旋球初速度偏右。空中飞行时，旋转所产生的气流与球四周的空气阻力都垂直，所以旋转对飞行弧线影响不大。

顺旋球着台时，球给台面一个向左的摩擦力，台面给球一个向右的反作用力，但是由于发球时球具有向左的初速度，所以虽然球受到向右的力，球不一定是第一次触台就向右侧弹起，如果不挡球只观察发球，可能n次触台后才向左侧弹起。同理，逆旋球也可能几次触台后才向右侧弹起。图3是顺、逆旋乒乓球飞行弧线及受力分析图，图中“路线一”是触台一次后拐弯的情形，“路线二”是触台二次后拐弯的情形。乒乓球触台两次时接球者需回球，通常接球者从后往前挥拍，如果逆旋球在触台两次时拐弯，球向外侧弹起，预判不好容易漏球，感觉球好像不见了，网球中“消失的发球”应该是这种情形，即以逆旋转为主。

顺、逆旋球沿来球方向平挡，触拍后的反弹方向变化不明显。

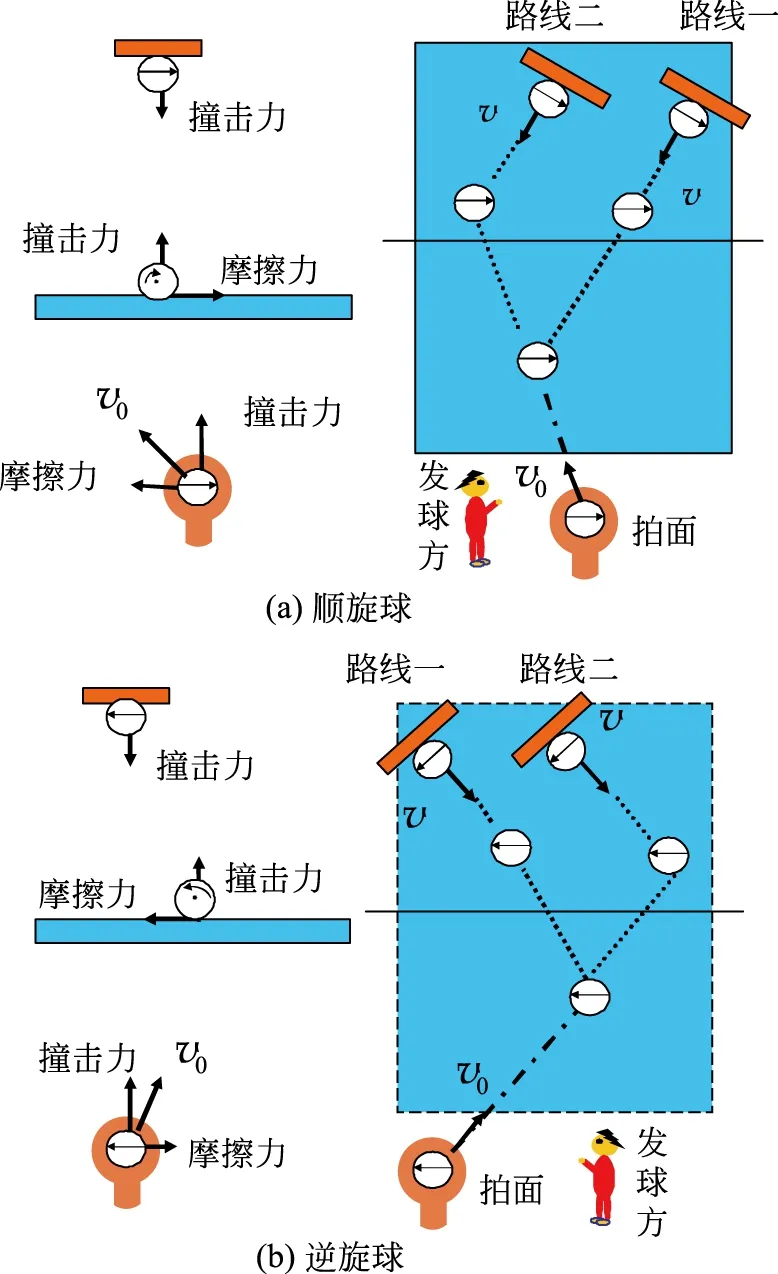
图3 顺、逆旋乒乓球受力分析及飞行弧线俯视图

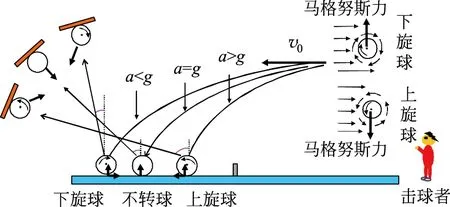
图4 乒乓球初速度相同时受力分析及飞行弧线侧视图

1. 3 上、下旋球

下旋球在飞行期间，下沿气流与迎面气流方向相反，流速减慢，上沿气流和迎面气流方向相同，其流速加快，根据伯努利方程，空气给球一个向上的马格努斯力。反之，上旋球受到向下的马格努斯力，如图4中所示。对于上、下旋球，主要讨论还击球的弧线。

如果上旋、不转、下旋3种球的初速度水平分量相同，那么落点的远近则与飞行时间成正比。假设这3种球的速度大小和方向都相同，则可忽略初速度对飞行时间的影响，上旋球由于受到向下的马格努斯力缩短飞行时间，与不转球相比，飞行曲线弯曲度大[6]，弧高要低，落点近。下旋球受到向上的马格努斯力，延长飞行时间，曲线平缓，弧高要高，落点远。如图4中所示。

上旋球着台时，球给台面一个向后的摩擦力，台面给球一个大小相同、方向向前的摩擦力，从而使球反弹时，与台面法线方向夹角增大，前进速度加快。下旋球反之，速度减慢，与台面法线方向夹角减小，甚至出现回跳现象。如图4中所示。特殊情况：如果下旋产生的升力和重力相当或大于重力，那么触台后球弹起不明显，且受到向后的摩擦力。球不弹起，对于必须着台后才回击的乒乓球来说基本无解，但这种发球出现概率比较低，在乒乓球中经常称为发球得分的“运气球”，在网球中称为“零式发球”，因为网球和地面摩擦力大，抓地能力强，受到向后的摩擦力，球还可能会朝网的方向滚动。

上旋球触及平挡拍面时，给拍面一个向下的摩擦力，拍面给球一个向上的摩擦反作用力，从而使球向上方反弹。下旋球反之，向下方反弹。如图4中所示。

将初速度水平分量相同的上、下旋球与不转球进行对比，考虑到初速度的影响：向上的初速度分量延长飞行时间；向下的初速度分量缩短飞行时间。初速度和旋转产生的影响互相制约，则可能出现任意远近的落点，分别考虑初速度和上、下旋结合的4种球。

初速度向上和下旋都是增加球的飞行时间的因素，所以初速度向上的下旋球比不转球落点远。比如高尔夫球，能打到200米开外[7]。乒乓球削球时，“兜”起球的这个动作和高尔夫的挥拍相似，削球一般球速慢[8]，飞行弧线长；反之，初速度向下和上旋都是缩短球的飞行时间的因素，因此初速度向下的上旋球和不转球相比落点近。这两种情形的落点远近与图4中类似。

将初速度向上的上旋球和初速度向下的下旋球进行对比，初速度的水平分量相等时，分析两种情形，第一种，初速度对飞行时间的影响力大于马格努斯力时，则上旋球的落点远。打球时，人们感觉上旋球容易出界，下旋球容易落网，则是这种情形。如图5(a)所示；第二种，马格努斯力的影响大于初速度时,则下旋球的落点远，如图5(b)所示。两种情形的共同点：由于受到向下的马格努斯力，上旋球的曲线弯曲度大；反之下旋球平缓。

图5 初速度水平分量相同时乒乓球可能的飞行弧线对比

足球中的“电梯球”，人们感觉像是球迅速升到六楼后，又急速地降到一楼。冯等研究“电梯球”，主要研究下旋球受到升力的变化规律[9]。笔者认为“电梯球”的初始飞行轨迹迅速上升，并不是受到升力，而是球初速度具有向上的分量。和普通不转球相比，反而是受到了向下的马格努斯力，因此，球的下坠速度会加快，人们感觉像是坐电梯一样。这也比较符合意大利教练安切洛蒂的描述：“球刚发出的时候有弧线，但到了中途下坠得特别快，整个弧线都不高。”弯曲度大但弧高并不高，正是上旋球受到向下马格努斯力的表现。而人们还描述“电梯球”飞行过程中基本不自身旋转，一方面，应该是对比“香蕉球”，没有侧旋，在水平方向上没有拐弯；另一方面，如果把足球看作质点，它上升到最高点的时间和自旋的周期相比拟，自旋可能被忽略了[10]。综上所述笔者认为“电梯球”应该是上旋球，飞行弧线参看图5(b)中的上旋球轨迹。

2 实例分析

以“金左脚”卡洛斯1997年经典“香蕉球”为例。考虑到卡洛斯踢该球时的发力：“我罚定位球时总是踢球的气嘴，因为那是球最硬的部位，你更能发力。我总是从左下角往右上角踢，这样踢出的球更有弧度。”也就是卡洛斯踢该球不仅有侧旋，还有上旋。

设置题目如下: 已知1997年卡洛斯踢出经典“香蕉球”时，足球距离球门40米，进球时间大约2秒，竖直方向高度参照球门高度2.44米，该球最高点大约为2米，近似卡洛斯踢该球初速度和3个轴的夹角都相同，且上旋成分和侧旋成分一样，也就是因侧旋和上旋产生的马格努斯力大小一样。仅考虑重力和因球旋转所产生的马格努斯力，(1)求该球在水平方向的最大偏移量；(2)仅考虑足球在水平方向上的分运动，按足球质量为M=0.44kg、半径R=0.11m、空气密度为ρ=1.29kg/m3，求该球绕质心转动的角速度ω是多少。

(1) 设水平向右为x轴方向，受到向左的马格努斯力，马格努斯力产生的加速度大小用a表示，前进方向为y轴方向不受力，保持匀速运动，向上为z轴方向，受到向下的重力和马格努斯力(和水平方向受到的马格努斯力大小一样)，则可得

对速度积分可得运动学方程为

根据球离球门40m，进球时间大约2s，初速度和3个轴的夹角相同，可得

vx0=vy0=vz0=20m/s

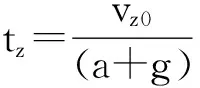
vx=0时，可得到水平面最大偏移量的时间：

a=90m/s2

马格努斯力产生的加速度a大概为9个重力加速度。

卡洛斯踢出的“香蕉球”如果上旋成分和侧旋成分一样，则到达最高点的时间要早于水平方向最大偏移的时间；z轴方向最高点小于水平方向最大偏移量。与实际观察结果非常吻合。

(2) 根据同一高度的伯努利方程，该球左侧压强p1和速度v1与右侧的压强p2和速度v2满足下式：

且v1=vxy+ωR，v2=vxy-ωR

气流对球的侧向压力为

补充说明: 近似处理法是物理学研究的基本思想方法之一，可以突出主要因素，简化物理过程。根据前面受力分析，在水平面内，横向的马格努斯力始终与速度方向垂直，就像带电粒子在磁场中的偏转，所以足球轨迹水平面内投影更接近圆周运动，虽然卡洛斯的这个进球已经是难得一见，但是也不排除，在未来的某一场比赛中，旋转的足球可能像回旋镖一样飞回踢球者身边。但是考虑到重力作用，足球通常只完成部分圆弧就落地了，当我们分析很大一个圆中的一小段弧线，可以把半径方向近似于垂直弧线方向，所以题(1)的分析中是把变力等效成恒力来求解的：把在水平面上马格努斯力近似恒为向左；竖直方向的马格努斯力近似恒为向下。

3 结论

(1) 球的自旋与初始速度存在着必然的联系。侧旋球的空中飞行过程中，因旋转而产生的马格努斯力并不是飞行轨迹产生“初始偏移”的原因，初速度才是，马格努斯力反而是使之“回旋”的原因。顺、逆旋球在触台时，拐弯时机与初速度有关。上、下旋球的落点远近也与初速度有关。所以初速度是分析旋转球飞行曲线的不可或缺的因素。

(2) 足球中的“香蕉球”(网球中的“蛇球”)以侧旋为主，“消失的发球”以逆旋为主。“电梯球”以上旋为主，“零式发球”以下旋为主。

[1] 郭振.浅析足球运动中的“电梯球”[J].体育世界:学术版，2015(5):10-11. Guo Zhen. Analysis of “elevator ball” in football[J]. Sport world(Scholarly)， 2015(5): 10-11. (in Chinese)

[2] 张三慧.大学物理学简程[M].北京：清华大学出版社，2010.

[3] 周道祥.从“野渡无人舟自横”到“香蕉球”技术[J].力学与实践，2005(3):94-95. Zhou Daoxiang. Analysis of “banana ball”[J]. Mechanics In Engineering. 2005(3): 94-95. (in Chinese)

[4] 刘建和.乒乓球教学与训练[M].北京：人民体育出版社，2004.

[5] 胡锐，邹祖莉.“香蕉”球的奥秘与物理学中的力学原理[J].物理教学探讨，2006(12): 21-22. Hu Rui, Zhou Zuli. The mystery of “banana” ball and mechanics principle in physics[J]. Journal of Physics Teaching，2006(12): 21-22. (in Chinese)

[6] 苏卫红.乒乓球旋转球的力学分析[J].雁北师范学院学报，2002(2):86-88.

Su Weihong. Analysis of mechanics of spinning ball[J]. Journal of Yanbei Normal University. 2002(2): 86-88. (in Chinese)

[7] 赵致真.从香蕉球说开去[J].力学与实践，2008(3):112-114. Zhao Zhizhen. Speaking from the banana ball[J]. Mechanics In Engineering. 2008(03): 112-114. (in Chinese)

[8] 吴焕群,秦志锋,许绍发,等.乒乓球旋转的定量研究[J].天津体育学院学报，2000(1):59-61. Wu Huanqun, Qin Zhifeng, Xu Shaofa, et al. Quantitative analysis of spin[J]. Journal of Tianjin Institute of Physical Education. 2000(1): 59-61. (in Chinese)

[9] 冯敏,从曙光,郑百林.不同运动条件下足球气动力及流场分析[J].力学与实践，2015(4):518-522. Feng Min, Cong Shuguang, Zheng Bailin. Aerodyamics and fluid analysis of soccer ball under various motion states[J]. Mechanics In Engineering. 2015(4): 518-522. (in Chinese)

[10] 韩同康.乒乓球的动态特性——旋转与速度相对原理[J].体育科学，1994(6):48-56. Han Tonggeng. Dynamic characteristics of table tennis—Relative principle of rotation and velocity[J]. China Sport Science.1994(6): 48-56. (in Chinese)

[11] 张汉壮，王文全.力学[M].北京：高等教育出版社，2009.

ANALYSIS OF THE FORCE AND THE FLYING ROUTE OF ROTATING BALLS WITH TABLE TENNIS AS AN EXAMPLE

Zhao Lite Fan Donghua Chen Yizhan

(School of Applied Physics and Materials, Wuyi University, Jiangmen Guangdong 529020)

It is helpful to improve the students' interest in learning physics to explore some interesting physical phenomena in sports. In this paper, six kinds of basic rotations and flying routes of table tennis are analyzed in detail by the basic laws of mechanics. The influence of initial velocity on flight route is discussed. Then, some interesting phenomena in the other ball games are discussed. For instance, the “snake ball” (“banana ball”) is mainly sidespin, the “disappeared serve” is mainly counterclockwise spin, the “lift ball” is mainly topspin, and the “zero serve” is mainly backspin. Detailed analysis of Roberto Carlos's banana free kick in 1997 was calculated and the quantitative results are given for the offset distance and angular velocity horizontally.

table tennis; rotation; banana ball; snake ball; lift ball; zero serve; disappeared serve; Magnus force

2016-04-20；

2016-11-21

广东省协同创新与平台环境建设专项资金项目资助(2014A070711024)；五邑大学校级教学质量工程项目资助(JG2014014)；五邑大学青年基金项目(2015zk13)；广东省高校创新团队项目资助(2015KCXTD027)。

赵丽特，女，讲师，主要从事物理教学科研工作，研究方向为物理教育和功能薄膜材料，zhaolite@126.com。

赵丽特，范东华，陈毅湛. 以乒乓球为例分析旋转球的受力及飞行轨迹[J]. 物理与工程，2017，27(2)：56-60,76.