力学分析中的正号与负号

陈奎孚 何坤娜

(中国农业大学理学院74#，北京 100083)

力学分析中的正号与负号

陈奎孚 何坤娜

(中国农业大学理学院74#，北京 100083)

力学关系的矢量形式整齐简明，但手工计算往往倾向于投影的标量式。不少学生在标量分析过程中有正负号的纠结。笔者对如下学习情境中的正负号纠结进行了剖析：物理关系、运动量、功、力矩、力偶和力矢量图示。指出消除正负号纠结的关键在于是否画矢量形式的分析图。基于矢量关系的演绎不需要图示信息,但手工计算总是喜欢用图形。有图形情形下，方向相反的矢量关系会由图形显示，标量关系就无负号。理解上述原则有助于提升力学分析的教学效率。

力学教学;力矢量;力偶; 惯性力主矢；惯性力主矩;功；运动量；阻尼振子；隔离体图

0 若干典型纠结

力学教学中常常遇到用正号还是负号的纠结，比如文献[1]例2～5中有“小球的粘滞阻力与其运动速度成正比，即fτ=kv,k为比例常数……”，而在文献[2]中有“物体所受的弹力f与弹簧的伸长量即物体相对平衡位置的位移x成正比，即f=-kx…”。我们知道：粘滞阻力与相对速度方向相反，但fτ=kv前没有负号；弹力f=-kx中的负号是因为弹力与偏离平衡位置的位移x方向相反。对专业物理教师而言，上述看似冲突的表述是能理解的，但对于学习物理课程而言的学生，他们更需要清晰一致的表述。

理论力学的受力分析也经常出现正负号的纠结，比如图1(a)的受力分析画成图1(b)是否正确[3]。很多学生会觉得图1(b)中的杆会向右加速而无法保持平衡，因此认为它是错误的。

图1

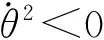
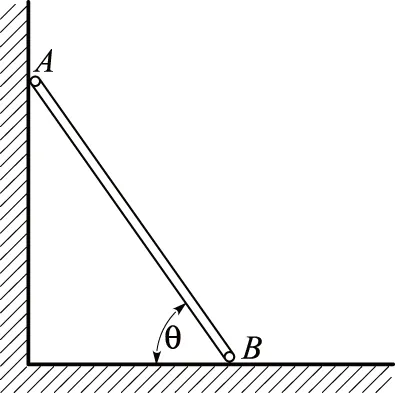
图2

在学习物理关系、运动量、功、力矩、力偶和力矢量等知识点过程中经常出现正负号的纠结，本文将对它们逐一分析。

1 物理关系中的正负号

文献[1]和文献[2]的两个例子都使用了标量符号。本质上力是矢量，只是教学中学生对矢量的感觉比较差，所以就习惯性地使用标量了。如果回到矢量，粘滞阻力应该写成fτ=-k，弹力应该写成f=-kx。对这两个矢量关系，都有负号。同样作用力f和反作用力f′之间的关系f=-f′，惯性主矢fI=-maC(C为质心)，也都有负号。

矢量既包含大小，也包含方向，所以采用矢量分析，无需画矢量分析图。运用矢量运算规则，既能得到所有信息，而且最终矢量也能够把信息完全表达出来。

由于矢量的使用门槛相对较高，所以从启蒙的初中物理开始，教师就习惯让学生使用受力图来分析受力，特别是高度频繁出现的平面问题，也正适合二维图形的表达。只要一旦有受力图，我们就会充分地利用图形呈现分析信息，特别是呈现其中的方向信息。因而如果图形已经呈现了恰当的方向信息，那么标量关系就不再加负号了。本文开头所举的两个例子正是这样：文献[1]关于粘滞阻力有受力图，受力图中fτ矢量方向与v=dy/dt指向相反，所以有fτ=kv；而文献[2]对弹力的描述无对应的矢量图，所以有f=-kx。

同理，如果像图3(a)那样画出了作用力与反作用力的矢量分析图，那么配合此图的关系是f=f′，而不是f=-f′ (如果没图，就必须使用f=-f′)[6]。在图3(b)中，惯性主矢方向与加速度方向相反的关系已经由图示虚线箭头的方向表示了，所以fI=maC(m为刚体质量;aC为质心C的加速度)而不是fI=-maC。类似地，惯性力系主矩MI=JCα(α为刚体转动的角加速度；JC为刚体绕C的转动惯量)。

图3

不少同学喜欢按图3(c)的方式标注惯性力系的主矢，这很容易出现下面的纠结：如果沿aC写投影方程，虚线箭头所表示的矢量沿aC的投影应该写成-maC还是maC呢？正确答案当然是前者。然而，如果只看该图，虚线箭头方向与aC相反，所以投影应该有负号，再乘上图上标注的-maC的负号，从而得到maC，这当然是错误的。为了避免上述纠结，把图中的-maC换成maC是否可行呢？答案是否定的，因为从图上来看，虚线箭头所示的矢量方向与aC相反，但是maC和aC却是方向相同的矢量。与此相反，图3b所采取的方式“矢量方向相反根据图示，再补上代数关系fI=maC”，肯定不会出现困惑。

图4

为了避免纠结，分析图上的矢量标注尽可能使用符号，不要用-maC这样运算式。符号尽可能唯一(不要用一个符号标注两个以上矢量)，尤其是带负号的情形更应避免。比如，图3(d)物体受到力偶作用，B点受力标注成-F，这容易引发B点受力究竟是向上还是向下的困惑。如果采用A点力矢量标为FA，而B点的力矢量标为FB，再补上代数关系FA=FB=F，肯定就不会出现纠结(更简洁的标注是用F和F′)。

2 运动量的正负号

在讨论图2的角位移和角速度的正负号之前，我们先看直角坐标量之间的正负号。

2.1 直角坐标

质点运动位移r，速度和加速度a之间的关系为=dr/dt和a=d/dt，它们不涉及正负号。上述矢量关系反映到直角坐标上，就可能会有潜在的问题，如直角坐标系原点不固定的情形。

坐标原点必须固定的要求容易理解，但操作起来有时会被忘记，比如图4(a)所示的机构, 由于B点在O的左边，因而很多同学会把坐标原点放在B上，从B指向O为x轴。若确实这么做，那么vDx=dxD/dt还是vDx=-dxD/dt呢？

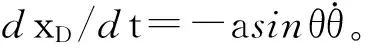
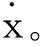
上述讨论看似画蛇添足，下面用图5(a)的粘性阻尼振子的受力分析来体会一下(图中c为阻尼器粘性系数)。先不妨假定质点的位移x>0。显然质点在x处的速度既可能向右(沿x轴正向)，也可能向左(沿x轴负向)。因为粘性阻尼力与速度方向相反，而受力图的重要作用是反映力矢量的方向信息，所以严格说来，受力图应该分别画向左和向右两种情形，即图5(b)和5(c)(重力和支持力对振动无实质贡献，略去不画)，图中Fk和Fc分别为弹力和阻尼力。两种情形下质点所受的合力均为FR=Fk+Fc，这是矢量加，不用参考受力图。把Fc=-c，得到FR=Fk-c，这是矢量替换，同样也不用参考受力图。显然FR沿水平方向，设其与x轴指向相同，我们来写投影式，这必须参考受力图。对图5(b)有

FR=-Fk-Fc

(1)

与图5(b)相配的阻尼力标量式为Fc=cv(没有负号，相反关系由图中相反的箭头所示)，代入式(1)得到(注意：代入过程不用去琢磨受力图，忘记受力图，直接代数运算)

图5

(2)

而参考图5(c)的投影方程则为

FR=-Fk+Fc

(3)

对图5(c)，阻尼力标量式依旧为Fc=cv,代入式(3)有

FR=-Fk+cv

(4)

式(2)和式(4)形式上有差异，此外为了得到式(2)和式(4),需要画两幅受力图。

(5)

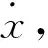
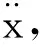
(6)

(7)

(8)

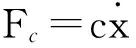
中学物理大多仅讨论到直线上的物理量，这使得坐标系意识淡薄，故而更容易出现纠结[9]。

总之，用坐标和坐标的导数，而不是用距离(速度和加速度)，分析过程会相对简洁，出现类似文献[10,11]的纠结要少一些。

2.2 角坐标

对转动量，如角速度、角加速度，一般有“逆时针为正，顺时针为负”规则。使用该规则时，我们是不参考图形的。如果有图形存在，我们则会参照图形标记的转向信息。当使用图形来反映转动量时，我们需要固定的参考体和参考转向。其中固定参考体应是无转动的刚体。参考转向一般选择逆时针转向，以与“逆时针为正”规则一致(必要情况下，参考转向也可以选择顺时针转向)。

图2中地面无转动，AB杆运动。如果选择地面为参考线，逆时针转动到AB杆，则角位移应为图6(a)中的β(β=π-θ),这样AB杆的角速度dβ/dt=d(π-θ)/dt=-dθ/dt。

图6

因为参考转向与正负号关系密切，所以笔者建议：表示角度用双箭头弧，而表示角位移用单箭头弧，箭头自参考线出发，转到运动物体。

3 功计算中的正负号

力F作用点经过元位移dr所做的元功为

δW=F·dr

(9)

上式进一步可表示为

δW=Fxdx+Fydy+Fzdz

(10)

式(9)不用参考任何图形信息，式(10)需要参考坐标轴的指向信息。在手工计算中，式(10)的使用比式(9)要频繁。

给出力的投影和作用点的微分，即可套用式(10)。比如图4中力F1的功。按照图4(c)的坐标系,

xA=(b-2a)cosθ,yA=bsinθ

(11)

F1的投影

Fx=F1sinθ,Fy=-F1cosθ

(12)

此处Fy右边的负号源自F1沿y轴投影的指向与y轴指向相反。

一旦写出式(11)和式(12),就无需再参考图形，直接把它们代入公式(10)即可。在套用前，计算坐标的微分，即

dxA=-(b-2a)sinθdθ, dyA=bcosθdθ

(13)

注意dxA右边括号外的负号来自对cosθ求微分的数学运算，与图形无关，更不用参考图形。

把式(12)和式(13)代入式(10),得到

δW=-(b-2asin2θ)F1dθ

(14)

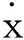
整理后得到与式(14)相同的结果。

虚位移原理涉及虚功的计算。虚功的坐标变分与普通的坐标微分几乎相同，所以上述正负号的讨论也适用于虚功的计算。

4 力矩计算中的正负号

平面力矩的常用计算方式有两种。第一种方式根据定义：力矩大小等于力臂与力大小乘积，正负号遵循“逆时针为正，顺时针为负”。该方法通常称几何法，它是需要参考图形的，因为矩心-力作用线相对位置和力指向这两个信息需要从图中获得，比如根据图7(a)的几何信息，我们有

MO(F1)=F1d1,MO(F2)=-F2d2

(15)

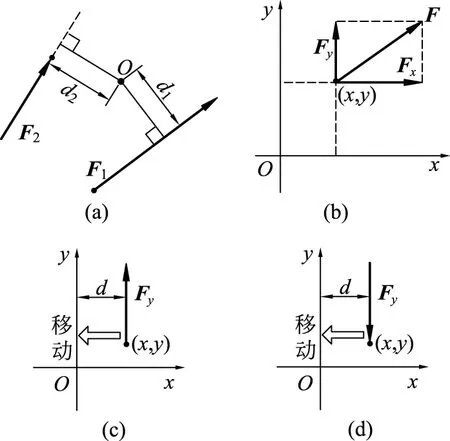
图7

第二种方式是使用下式计算(参见图7(b))

MO(F)=xFy-yFx

(16)

其中:(x,y)为力作用点坐标;(Fx,Fy)为力的投影。采用式(16)的计算，无需参考图形信息。计算结果MO(F)遵循“逆时针为正，顺时针为负”，也不用参考图形。当然写(Fx,Fy)需要参考坐标系。

式(16)是正确无误的。如果从空间的力矩矢r×F在xOy坐标面内投影的演绎来看，它也是很自然的。然而，作为教学，力矩概念无疑都是从平面定义开始的，然后接着介绍式(16)。教学中往往只是用图7(b)的第一象限的特殊情形对式(16)加以验证。若严格验证，则有16种情形之多。这是因为力矩计算涉及到坐标的正负号和力的指向，考虑(x,y)正负与(Fx,Fy)指向的组合，就有16种之多。显然，采用枚举式的验证过程就十分冗长。为了简化证明，可以根据合力矩等于分力矩之和的性质，先分别考虑Fx和Fy的矩。

先看Fy。在图7(c)中，有M(Fy)=dFy=xFy，此时为逆时针。当Fy向左移动，M(Fy)减小，当x<0时，M(Fy)=-dFy=xFy为负值，这确实对应M(Fy)的顺时针转向。在图7(d)中Fy向下，对O点的矩为顺时针，相应地M(Fy)=xFy<0(因为力的投影Fy<0，投影值参考坐标轴的指向，不是图示的Fy指向)。当Fy向左移动到x<0，Fy对O的力矩变成逆时针，当然M(Fy)=xFy也确实大于零了。

综上所述M(Fy)=xFy对坐标的正负和Fy指向的所有组合都成立。类似地考虑Fx，可知M(Fx)=-yFx对坐标的正负和Fx指向的所有组合都成立。根据合力矩性质有

M(Fy)=M(Fy)+M(Fx)=xFy-yFx

这就证明了式(16)。

力偶矩的转向和力矩的转向没有本质差异，所以上述讨论也适用于力偶矩。最常提及力偶矩规则是“逆时针为正，顺时针为负”。这个规则适用的场合是没有图形信息，如M=40N·m表示逆时针转向的力矩，大小为40N·m，而M=-30N·m表示顺时针转向的力矩，大小为30N·m。

然而，力学分析喜欢使用图形。一旦有图形，总是把图形示意的转向为参考转向，比如图8中4个带箭头的弧标明了参考转向，弧箭头旁边的符号M1,M2,M3,M4表示力矩的数值，它要另行补充，比如M1=10N·m,M2=-20N·m,M3=30N·m,M4=-40N·m。M1=10N·m的数值与图示的弧箭头转向一起表示这是大小为10N·m的逆时针转向力偶。此时，不能因M2=-20N·m中有负号而认为它是顺时针转向，而是因为有了图形，数值和图示转向一起表明M2是大小为20N·m的顺时针转向作用的力偶。M3=30N·m也不表示它是逆时针。参考图示转向，它是大小为30N·m的顺时针转向作用的力偶。类似地M4=-40N·m与图示参考转向一起，表明M4大小为40N·m的逆时针转向作用的力偶。

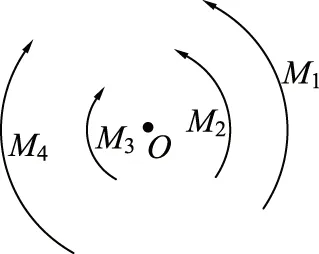
图8

5 力矢量的指向

既然平面力偶矩可以用图示参考转向与数值联合的方式来表示，那么平面力矢量也当然可以用图示参考方向与力的数值来表示。如同力偶的数值，力的数值也可以取负值。这就消除了图1b的纠结，即图中约束力FBx和FBy的数值取负值，从而AB能杆保持平衡。

通常说矢量有方向和大小(范数或模)两个属性，而平面矢量又往往用几何图示，而几何大小的“常规语义”是不包括负值的。如果想刻意突出包含负值，笔者建议用矢量的“数值”这一词汇。当然有人可能质疑出现代数符号怎么办。从词法上讲，代数也是“数”，代数值也是“数值”，就如同不等式也是“式”一样。

图9

为什么刻意强调力矢量的数值可以为负呢？通常，物理教学的受力分析相对简单，学生不仅能判断出力的作用线，而且也容易确定数值为正的指向。然而在受力比较复杂情形下，特别是当研究对象由多物体组成时，很难正确判断出正数值的指向。这种情形下，我们把作用线方向判断对了即可，而指向可先假定，然后由力学方程确定数值的正负。

上述处理并不影响分析结果，而且有助于复杂情形的力学分析。这里通过举例说明。图9(a)中F=20 kN,M=10 kN·m, 几何信息如图示，分析B铰和固定端C处的约束力。

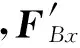
上述答案的负值，表明正数值方向(转向)与图示的相反。但无需重新画图(以便出现正的数值)，因为数值和图示方向(转向)一起给出了完整的力信息。

为了校核上述处理的合理性，图9(d)和9(e)是把FBx和FBy按正数值指向方式画的(本题容易知道正数值对应的指向)。对这两个图列平衡方程求解得到

对比式(17)和式(19),发现B铰约束力的数值确实由负变正了。式(18)和(20)相同，表明B铰约束力方向的假设并不影响其他地方的受力分析结果。

总之，对于复杂的力学分析，约束反力的作用线在受力图中要正确，而其正数值的指向可留待由力学方程确定。也正因为图示指向和力学方程所确定的数值一起表征了力的完整信息，所以受力图在分析过程中不能缺席。

6 结语

力学学习中可能涉及正负号纠结的情景有物理关系、运动量、功计算、力矩、力偶和力矢量指向等。 本文对这组情景下的纠结进行了分析，得到了如下看法：

1) 用矢量表述的物理关系，不需要参考图形信息，不存在正负号的纠结。

2) 如用图形表示矢量信息，则矢量的方向反映在图形上。方向相反的两个矢量，已经由图形示意反向了，投影的标量式就不要再有负号了。但是随后的计算分析必须参照图形进行。结果解释也要参照图形信息。

3) 对基于图形的分析方法，比如受力图，因为图形上有力的作用线和假定的指向信息，所以必须要画出受力图，答案才是完整的。

4) 坐标的各阶导数的指向与坐标轴指向相同。利用这一性质，可简化动力学分析过程。

[1] 王少杰，顾牡，毛骏健.大学物理学(上册) [M].2版.上海：同济大学大学出版社，2002.2:29.

[2] 王少杰，顾牡，毛骏健.大学物理学(下册)[M].2版.上海：同济大学大学出版社，2002.5:103.

[3] 陈奎孚.理论力学自主学习解题辅导[M].北京:中国农业大学出版社，2014,12:5.

[4] 叶玉琴.一道力学题的求解及感悟[J].中学物理，2011,29(21):20-22. Ye Yuqin. Solving a mechanics problem and its reflections[J]. Zhongxue Wuli (Gaozhong Ban)， 2011, 29(21): 20-22. (in Chinese)

[5] 陈奎孚.中学物理教育应该强基础重通适——一位大学教师的视角[J].物理与工程，2016,26(4):22-26. Chen Kuifu. High school physics education should highlight the corner stone knowledge and underline the universal approach[J]. Physics and Engineering. 2016, 26(4): 22-26. (in Chinese)

[6] 胡扬洋,耿爱霞.物理教材“牛顿第三定律”编写存在的三个疑难问题[J].课程教学研究,2014,(1):76-79. Hu Yangyang, Geng Aixia. Three perplexities pertaining to the Newton Third Law in composing physics textbooks[J]. Journal of Curriculum and Instruction, 2014, (1): 76-79. (in Chinese)

[7] 陈奎孚.机械振动教程[M].北京:中国农业大学出版社，2014,4.

[8] 刘荣暄.理论力学中的正负号问题[J].力学与实践,1994,(2):55. Liu Rongxuan. The issue of plus and minus signs intheoretical physics[J]. Mechanics and Practice, 1994, (2): 55. (in Chinese)

[9] 庞春晨.高中物理教学如何规范使用正负号[J].理科考试研究，2015,(23):47. Pang Chunchen. How to determinelogically the plus sign or the minus sign in high school physics education[J]. Examinations Research Science, 2015, (23): 47. (in Chinese)

[10] 赵俊霞.一道错解题的思考[J].中学物理，2013,31(3):66-67. Zhao Junxia. Reflections to afallacy solution[J]. Zhongxue Wuli(Gaozhong Ban), 2013, 31(3): 66-67. (in Chinese)

[11] 郑永圣,黄修斌.关于《一道错解题的思考》一文的商榷[J].中学物理，2013,31(23):43-44. Zheng Yongsheng, Huang Xiubin. Comments on ‘Reflections to afallacy solution’[J]. Zhongxue Wuli(Gaozhong Ban)， 2013, 31(23): 43-44. (in Chinese)

ON THE PLUS AND MINUS SIGNS IN MECHANICS ANALYSIS

Chen Kuifu He Kunna

(College of Sciences #74, China Agricultural University, Beijing 100083)

The vector form of mechanics relationship is concise and tidy whereas the projected scalar form is preferred to in manual computation. Plenty of students are frustrated with choosing plus or minus signs in scalar form computation. The frustration with plus or minus signs are investigated in the following contexts, physics relationship, kinematic quantities, work, force moment, force couple and force vector graphing. It is pointed that a key factor is whether the vector diagram is drawn or not. The vector form of relationship does not necessitate a vector diagram; as a result, there is no need to consider the plus or minus sign. On the other hand, a vector diagram is preferred, especially in the case of planar problems. Concerning this case, the opposite directions of two vectors are delineated in the diagram; as a result, the minus sign should not appear in the scalar relationship. Apprehending above rules benefits the educational efficacy of force analysis.

mechanics pedagogy; force vector; force couple; principal vector of inertia; principal moment of inertia; power; kinematical quantity; damped vibrator; free body diagram

2016-09-10

陈奎孚，男，教授，从事力学和振动的教学研究,chenkuifu@cau.edu.cn。

陈奎孚,何坤娜. 力学分析中的正号与负号[J]. 物理与工程，2017，27(2)：15-21.