基于改进风险顺序数的产品质量功能展开方法
严正峰, 程伟平
(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)
基于改进风险顺序数的产品质量功能展开方法
严正峰, 程伟平
(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)
为提高产品设计质量,文章提出了一种基于改进风险顺序数(risk priority number,RPN)的质量功能展开(quality function deployment,QFD)方法。该方法用层次分析法(analytic hierarchy process,AHP)确定RPN中各因子的权重;针对RPN中专家评判的模糊性和不确定性,基于粗糙集理论提出了改进的逼近理想排序法(technique for order preference by similarity to ideal solution,TOPSIS),获得了产品失效模式对应失效原因的RPN排序和基本相对重要度;并以该失效原因对应的工程参数为QFD的工程特性,利用矩阵展开确定零件特性;引入了实现工程特性改进目标所要求的总资源、总可行性、产品竞争优势等概念,进而确定了工程特性基本相对重要度的修正因子,确定了工程特性的最终相对重要度;最后,以汽车离合器产品设计为例,验证了该方法的有效性和可行性。该方法同样适应于其他类产品。
风险顺序数(RPN);质量功能展开(QFD);粗糙集;逼近理想排序法(TOPSIS);修正因子
0 引 言
产品设计是一个创新过程,涉及包括顾客需求信息、质量信息以及产品设计相关领域的各类知识[1]。在这些需求信息中顾客最关注的就是产品设计的质量,为了满足顾客的高质量要求,采用质量驱动[2]的产品设计思想得到越来越多的应用。质量驱动产品开发方法应以质量功能展开(quality function deployment,QFD)和失效模式与影响分析(failure model and effect analysis,FMEA)为基础。
QFD是一种在产品开发过程中最大限度地满足用户需求的质量保证与改进方法,通常QFD过程包括产品规划、零部件规划、工艺规划和生产规划4个阶段。在产品规划阶段,确定工程特性重要度是质量屋构建过程中一个关键的步骤。文献[3]针对QFD中顾客需求和工程特性之间的关联关系以及工程特性自相关关系的不确定、不分明以及模糊等特性,分别提出关联关系和自相关关系确定的粗糙集方法,确定工程特性重要度;文献[4]提出了基于混合语言变量的工程特性重要度确定方法;文献[5]应用模糊加权平均法求解工程特性重要度;文献[6]采用网络分析法(analytic network process,ANP)确定QFD中工程特性的重要度;文献[7]将模糊理论与ANP法结合,以获取工程特性的重要度;文献[8]应用一种线性偏序方法对QFD决策过程中工程特性进行排序研究。但是上述工程特性转换时均没有考虑到失效及其后果影响的缺陷。
风险顺序数(risk priority number,RPN)是FMEA中最常用的确定多个故障模式风险优先次序的方法,其计算基于3个风险因素,即风险严重度(S)、风险频率(O)、风险可检测程度(D)。虽然FMEA已被认为是最有效的事前预防措施,但其风险评估方法却广受质疑。其中,RPN确定中有风险因素权重均分、各风险因素风险度量的主观和模糊性以及风险因素综合评价单一等缺陷。
针对上述问题,国内外学者进行了大量研究。其中,文献[9]建立了风险因子和RPN之间的推理规则,运用模糊FMEA方法评估失效;文献[10]基于模糊加权几何平均法,提出模糊RPN确定方法;文献[11]利用决策试验与评价实验室理论,构建失效模式直接影响关联图,提出模糊语境下的复杂系统关联FMEA法;文献[12]将RPN的各个因子视为语言变量,利用依赖型语言有序加权几何(dependent linguistic ordered weighted geometric,DLOWG)算子综合专家评估意见,对模糊环境下的FMEA风险评估;文献[13]引入粗糙逼近思想排序方法(technique for order preference by similarity to ideal solution,TOPSIS)来进行失效风险评估;文献[14]基于模糊层次分析法(analytic hierarchy process,AHP)和模糊TOPSIS结合的方法来确定失效的RPN。上述文献表明,许多专家致力于研究不同理论在FMEA中的运用,但模糊理论需要事先确定成员隶属度或隶属函数,而准确确定它们通常较困难。
因此,本文提出了一种基于改进风险顺序数的质量功能展开方法。首先通过AHP定量确定RPN中S、O、D的权重;然后,基于粗糙集改进的TOPSIS理论,通过相对贴近度计算RPN排序;最后,由RPN排序确定可靠性屋工程特性的基本相对重要度,引入基本相对重要度修正因子,计算得到工程特性的最终相对重要度,利用QFD的矩阵决策方法确定相应零件特性的权重和目标值。
1 基于改进风险顺序数的可靠性屋
QFD的基本概念是利用质量屋[15]将顾客需求映射到工程特性,并依次将其映射到后续的零件特性、工艺特性和生产特性。它虽然能够满足顾客需求并缩短产品开发周期,但是却无法在产品开发初期有效地发现并控制后续所产生的隐藏质量缺陷问题,导致整个产品在进入市场后仍不断有问题出现。
本文利用QFD与FMEA结合模型,将QFD方法中的矩阵展开思路应用于FMEA等可靠性分析中,在质量规划中考虑产品失效方面的影响[16]。将FMEA与QFD结合构建的可靠性屋如图1所示。其中可靠性屋的“左墙”来源于产品失效模式的原因,“屋顶”为零件特性自相关矩阵。可靠性屋提供了将可靠性概念或要求逐层转化为相应的可靠性工程特性的框架和结构。具体做法如下:利用企业产品数据,通过专家系统对产品进行FMEA分析,建立失效模式数据库;计算RPN的排序,利用KJ法对失效模式及其对应的失效原因进行分析,以失效模式对应的失效原因参数为QFD的工程特性,即可靠性屋的左墙。利用可靠性屋得到的零件特性重要度建立工程特性与零件特性的相关矩阵,通过QFD矩阵展开指导产品设计。
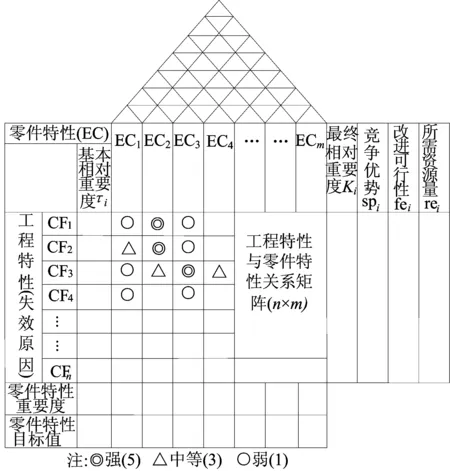
图1 可靠性屋
2 产品失效模式排序及权重确定
由于传统的RPN确定方法存在一些缺点和不足,本文引入一种结合AHP和粗糙TOPSIS理论的方法,计算产品的失效模式及失效原因的RPN排序,并确定工程特性的基本相对重要度。
2.1 AHP确定RPN中S、O、D的权重
AHP把多因素组成的相互关联、相互影响的复杂系统分解成一个具有层次化、条理化的多层次分析结构模型。该模型一般由高到低可分为目标层、准则层和方案层。
具体算法步骤如下:
(1) 建立层次结构图。
(2) 设各阶层判断矩阵为R。对每一层各元素关于上一层中某一准则进行两两比较,构造出判断矩阵,即
其中,R为正定互反矩阵,对于正定互反矩阵,RW=λmaxW,其最大特征根λmax存在且唯一。

2.2 基于粗糙TOPSIS的产品失效模式排序
(1) 构建产品失效模式评估矩阵。假定某一产品有n种失效模式,由于同一种失效模式可能对应不同失效原因,失效模式原因集为CF={X1,X2,…,Xn},Xi为第i种失效模式对应的失效原因发生的严重度(S)、频率(O)及可检测程度(D)的评估,专家采用传统(1~10)的打分方法,则产品失效模式的评估以矩阵的形式表达为:
(1)

设Z为论域Y中任一对象,将Y中的所有对象划分为m个,其集合U={P1,P2,…,Pm}。如果这m个划分有P1 (2) 而Pt的上近似集可以定义为: (3) 相应地,边界区域为: (4) (5) (6) 其中,NL、NU为Pt的相应近似集所包含的对象数目。则粗糙数为: (7) 由(2)~(7)式可以得到: (8) (9) 得到粗糙群决策矩阵为: (10) (3) 计算加权标准化决策矩阵的权重。不同的标准尺度采用如下归一方法处理,即 (11) 综合的粗糙群决策矩阵权重计算如下: (12) (4) 根据评价因子属于成本型还是效益型,TOPSIS法理论中的正理想解S+(j)和负理想解S-(j)表示为: (13) (14) (5) 计算每一种失效模式到正理想解和负理想解的距离。到正理想解距离和到负理想解距离分别为: (15) (16) 其中,i=1,2,…,n;j=S,O,D。则相对贴近度为: (17) (6) 计算失效原因的基本相对重要度,即可靠性屋工程特性基本相对重要度为: (18) 3.1 工程特性基本相对重要度的修正因子 QFD团队依据企业资源现状和产品改进意愿,引入了确定可靠性屋工程特性基本相对重要度的修正因子的定义。 定义1 工程特性基本相对重要度修正因子不仅取决于实现可靠性屋工程特性改进目标所需的总资源量,还取决于实现可靠性屋工程特性改进目标的可行性和产品竞争优势。 上述关系可利用如下函数表示工程特性基本相对重要度τi的修正因子,即 moi=f(rei,fei,spi) (19) 其中,rei为实现可靠性改进目标CFi(即失效模式原因)所需的总资源量;fei为实现可靠性改进目标CFi的可行性;spi为产品竞争优势。 修正因子必须满足的要求如下:实现可靠性改进目标总可行性越大,修正因子越大;实现可靠性改进目标的总资源量越少,修正因子越大;产品竞争优势越大,修正因子越大。 3.2 工程特性改进所要求的总资源和可行性 为实现可靠性改进,提高产品设计质量,实现工程特性改进目标,企业必须投入的(如资金、人力、企业与供应商之间的协同设计等各种有形资源,以及核心技术、团队成员的知识经验等)无形资源。因为各种资源可能并不具有相同的重要性,所以根据它们在项目中的相关性进行重要性排序。 要积极开展网络思政教育,引导大学生健康使用网络直播,学校可以适当的开设一些新的相关课程,把网络思政教育纳入到大学生日常教育过程中。思想政治教育工作者也需要紧跟社会时代的潮流,不断了解先进的思想观念,学习使用一些新型的平台,把传统的思想政治教育内容通过网络直播平台展示给学生,再将直播平台与大学生思想政治教育整合的过程中,可能存在一些问题,也需要思想政治教育工作者去学习去思考。直播平台是一种新型思想政治教育的载体,对思想政治教育的工作开展具有积极作用。另外,大学生思想政治教育工作者需要注意监管与引导,使大学生能够合理参与到网络直播中去。 为了简化,采用比例标度法确定各种资源的大小,并且利用AHP确定各种资源的相对重要性。因此,总资源为: (20) 产品设计中存在一个可行性的问题[18],QFD团队必须对其所涉及的项目实施可行性分析。产品设计团队为实现产品可靠性需求,对可靠性屋工程特性CFi进行可行性分析,以便提前发现风险,从而提高产品设计成功的可能性。为实现可靠性改进目标的总可行性,首先利用比例标度法确定实现可靠性改进目标CFi所需要的各种资源的可行性,而后利用“加权和”的形式确定其总可行性。 因此,实现可靠性改进目标的总可行性为: (21) 3.3 确定工程特性基本重要度的修正因子 确定工程特性基本重要度的修正因子也必须 考虑工程特性改进所带来的产品竞争优势。通常一个竞争优势强的产品质量可靠性高,一个中等竞争优势的产品具有不高的可靠性,产品竞争优势不明显。 通常把产品竞争优势分为3个等级,分别对应数值1.5、1.2、1.0。依据上述分析可知,为了简化计算,工程特性基本相对重要度的修正因子可以表示为: (22) 本文将风险顺序数结合于产品可靠性设计中,建立的产品质量功能展开流程如图2所示。 图2 产品质量功能展开流程 (1) 专家对产品进行失效模式与效应分析,利用以往产品使用中的故障信息以及故障原因,建立可靠性数据库。 (2) 假设共有Gi(i=1,2,…,n)个专家,利用AHP对数据进行群体决策处理,确定RPN中各因子权重。 (3) 假定某一产品有n种失效模式,对这n种失效模式分析可得到不同失效原因,失效模式原因集为CF={X1,X2,…,Xn} ,基于粗糙TOPSIS分析,得到这n种失效模式及原因的基本相对重要度 。 (4) 利用KJ法分析所得到的失效原因及其对应的参数,并以此为可靠性屋的工程特性,将上述的基本相对重要度与工程特性基本相对重要度的修正因子相乘,可得到工程特性的重要度, 即 ki=τimoi (23) 最后,经归一化处理,得到工程特性最终相对重要度为: (24) (5) 通过QFD矩阵展开,得到零件的特性和相对重要度。以所得到的零件特性相对重要度进行工艺设计矩阵展开和生产控制矩阵展开,实现对引起产品失效的工程参数按RPN排序配置不同的权重,指导产品设计,以保证产品的质量可靠性。 某汽车离合器公司为提高所生产的某一系列型汽车离合器的可靠性,采用基于RPN的质量功能展开方法,对汽车离合器进行保质设计。汽车离合器的主要功能是传递扭矩、切断动力和防止过载,常见的故障有打滑、分离不良、起步发抖、异响、踏板力过重以及异常损坏。其中打滑主要是扭矩容量不足,根据文献[19]可以明确摩擦片摩擦系数、压紧力、作用半径、作用点位置相关。本文对于汽车离合器常见的打滑这一失效模式,从盖及压盘总成和从动盘总成2个方面进行失效原因分析,结果见表1所列。 在本研究中选取了6位专家的数据用AHP进行群体决策数据处理,评估RPN中S、O、D因子的权重,判断矩阵见表2所列。判断矩阵的重要度计算和一致性检验结果为:λmax=3 018;一致性指标CI=0.009<0.1;S、O、Q因子的权重WS=0.625,WO=0.136,WD=0.239。 表1 某系列汽车离合器的失效模式与原因 表2 判断矩阵 RPN分析团队由4位技术专家组成,利用企业产品的失效模式数据库,对上述的失效模式分别从故障模式的S、O、D3个方面进行评价,结果见表3所列。 表3 专家对各失效模式原因的评分 由(2)~(12)式得到每种失效模式对应的加权粗糙群标准化决策矩阵权重,见表4所列。 表4 加权粗糙群标准化决策矩阵权重 在评价因子是成本型时,通过(13)~(17)式得到S+(j)、S-(j)和ξi的值,见表5所列。 表5 相对贴近度ξi的值 从表5中的数据可以看出,CF2的RPN排序最高,为该型汽车离合器最多发生的失效因素;CF6为最少发生的失效因素,排序最低。 QFD团队利用头脑风暴法确定工程特性改进目标所需的总资源量包括改进时间、改进费用、供应商能力、研发人员,利用AHP分析法确定各权重,计算出rei、fei、spi大小,从而利用(18)~(21)式得到汽车离合器产品的最终相对重要度,见表6所列。 表6 某系列型汽车离合器工程特性与零件特性二维展开结果 本文实例中从总摩擦系数的最终相对权重为22.10%,是影响该系列型汽车离合器的最主要因素。通过QFD展开,确定与从总摩擦系数有关的零件特性是摩擦片高温性能和摩擦片摩擦系数,这2个零件特性的相对重要度分别为13.95%和9.34%。在QFD功能配置过程中,由工程特性权重确定出零件特性的相对重要度,实现对影响产品设计质量的关键零件进行可靠性设计。同时由以上的零件特性的相对重要度,进行工艺设计矩阵展开和生产控制矩阵展开,使所设计的汽车离合器系列产品具有良好的质量。 (1) 本文通过AHP和粗糙TOPSIS方法,量化产品失效评估中专家评判的模糊和不确定性,得到各失效模式及其对应原因的排序。 (2) 以失效原因对应的工程参数为可靠性屋的“左墙”即工程特性,同时对工程特性基本相对重要度引入修正因子,确定工程特征最终相对重要度。 (3) 利用QFD对产品设计进行矩阵展开,确定相应零件特性重要度,实现产品设计中关键质量特性提取和关联权重计算,从而提高了产品设计的可靠性,保证了顾客的可靠性需求。 [1] PIRMORADI Z,GARY W G,SIMPSON T W.A review of recent literature in product family designand platform-based product development[M]//Advances in Product Family and Product Platform Design.New York:Springer,2014:1-46. [2] 龚勋,冯毅雄,谭建荣,等.基于全生命周期的质量驱动产品模型构建方法[J].计算机辅助设计与图形学学报,2011,23(10):1764-1769. [3] 李延来,唐加福,姚建明,等.质量功能配置中工程特性最终重要度的确定方法[J].机械工程学报,2007,43(4):178-186. [4] 王增强,李延来,蒲云.基于混合语言变量的工程特性优先度确定方法[J].中国机械工程,2013,24(20):2797-2803. [5] 何桢,赵有,马彦辉.模糊QFD中技术特性重要度排序方法[J].天津大学学报(自然科学与工程技术版),2008,41(5):631-634. [6] LIN Y,CHENG H P,TSENG M L,et al.Using QFD and ANP to analyze the environmental production requirements in linguistic preferences[J].Expert Systems with Applications,2010,37(3):2186-2196. [7] FEYZOLU Q,BUYUKOZKAN G.An integrated group decision-making approach for new product development[J].International Journal of Computer Integrated Manufacturing,2008,21(4):366-375. [8] HAN C H,KIM J K,CHOI S H.Prioritizing engineering characteristics in quality function deployment with incomplete information:a linear partial ordering approach[J].International Journal of Production Economics,2004,91(3):235-249. [9] CHIN K S,CHAN A,YANU J B.Development of a fuzzy FMEA based product design system[J].International Journal of Advanced Manufacturing Technology,2008,36(7/8):633-649. [10] WANG Y M,CHIN K S,POON G K K,et al.Risk evaluation in failure mode and effects analysis using fuzzy weighted geometric mean[J].Expert Systems with Applications,2009,36(2):1195-1207. [11] 伍晓榕,裘乐淼,张树有,等.模糊语境下的复杂系统关联FMEA方法[J].浙江大学学报(工学版),2013,47(5):782-789. [12] 王晓暾,熊伟.基于DLOWG算子的FMEA风险评估方法[J].浙江大学学报(工学版),2012,46(1):182-188. [13] SONG W,MING X,WU Z,et al.A rough TOPSIS approach for failure mode and effects analysis in uncertain environments[J].Quality and Reliability Engineering International,2014,30(4):473-486. [14] KUTLU A C,EKMEKCIOGLU M.Fuzzy failure modes and effects analysis by using fuzzy TOPSIS-based fuzzy AHP[J].Expert Systems with Applications,2012,39(1):61-67. [15] 年陈陈,江擒虎,陈远龙.基于QFD的电解加工工艺健壮设计方法[J].合肥工业大学学报(自然科学版),2014,37(2):141-144. [16] 杜雷,高建民,陈琨.基于故障相关性分析的可靠性配置[J].计算机集成制造系统,2011,17(9):1973-1980. [17] PAWLAK Z.Rough set approach to knowledge-based decision support[J].European Journal of Operational Research,1997,99(1):48-57. [18] KAY C T,VIJAYALAKSHMI R.Incorporating concepts of business priority into quality function deployment[J].Imperial College Press,2011,8(1):21-35. [19] 徐石安,江发朝.汽车离合器[M].北京:清华大学出版社,2005. (责任编辑 胡亚敏) Quality function deployment method of product based on improved risk priority number YAN Zhengfeng, CHENG Weiping (School of Automobile and Traffic Engineering, Hefei University of Technology, Hefei 230009, China) To improve the quality of products design, a quality function deployment(QFD) method based on improved risk priority number(RPN) was proposed. Firstly, the weight of each factor in RPN was determined with analytic hierarchy process(AHP). Secondly, to solve the fuzziness and uncertainty of expert evaluation in RPN, an improved technique for order preference by similarity to ideal solution(TOPSIS) was proposed based on the rough set theory, and the RPN rank and fundamental importance ratings of failure causes for the product failure modes were obtained. Next, with engineering parameters of the failure causes as engineering characteristics of QFD, part characteristics were determined by means of matrix expansion. Furthermore, concepts of total resource and total feasibility of achieving the improvement target of engineering parameters as well as product competitive advantage were introduced, then the fundamental importance ratings of the engineering parameters were appropriately corrected, and the final fundamental importance ratings of the engineering characteristics were determined. Finally, an example of automobile clutch product design was made to verify the effectiveness and feasibility of the proposed method. The method can also be applied to other products. risk priority number(RPN); quality function deployment(QFD); rough set; technique for order preference by similarity to ideal solution(TOPSIS); correct factor 2015-11-20; 2016-03-31 安徽省重点实验室建设资助项目(201106G01015) 严正峰(1969-),男,湖北黄梅人,博士,合肥工业大学教授,硕士生导师. 10.3969/j.issn.1003-5060.2017.05.002 TB472 A 1003-5060(2017)05-0582-08
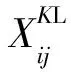


3 工程特性最终重要度确定


4 应用实例






5 结 论

