基于LTC1562-2芯片的声纳高频带通滤波器设计

石春华

(上海船舶运输科学研究所 舰船自动化分所，上海 200135)

基于LTC1562-2芯片的声纳高频带通滤波器设计

石春华

(上海船舶运输科学研究所 舰船自动化分所，上海 200135)

在声纳接收机中，滤波器是一个非常重要的组成部分，其性能的好坏直接影响接收信号处理的质量。采用LTC1562-2芯片代替LTC1562芯片,以Linear公司的仿真软件LTspiceIV和FilterCAD为辅助工具，结合理论计算。测试结果表明，所设计中心频率为200 kHz的巴特沃斯型带通滤波器可满足某型声纳接收滤波电路的使用要求，并根据仿真和计算结果进行了实际电路测试。

带通滤波器；LTC1562-2芯片；巴特沃斯；声纳

0 引 言

在水声通信中，为了使滤波器在通频带内的频率响应平坦和低噪声，一般使用多个二阶有源滤波器级联构成巴特沃斯型带通滤波器[1]。在声纳接收电路中，有些采用有源滤波器芯片LTC1562芯片构成多阶带通滤波器，现需设计中心频率为200 kHz的高频带通滤波器，带宽为20 kHz。然而芯片LTC1562的频率最大只有150 kHz,无法满足设计要求。在对多家厂商滤波芯片的选型进行比较后，选择使用Linear公司的LTC1562-2芯片作为200 kHz滤波器芯片。LTC1562-2芯片能满足设计中心频率为200 kHz的要求，功能上可实现8阶巴特沃斯型带通滤波器。同时，该芯片和原来的LTC1562芯片均是Linear公司的产品，并且封装与LTC1562芯片完全一致，可在对原有接收机改动最小的情况下完成高频滤波的改进，节约设计成本。

1 LTC1562-2芯片的结构及特性

LTC1562-2芯片是Linear公司推出的一款低噪声及低失真的连续时间模拟有源滤波器，可实现以20～300 kHz为中心频率的滤波器，其内部由4个二阶单元组成，每个二阶单元的中心频率f0，品质因素Q及增益Gain均可通过3个外部电阻或电容进行设置，可实现巴特沃思、切比雪夫和贝塞尔型等不同形式的低通、带通和高通滤波器[2](LTC1562-2芯片外部引脚见图1)。

图1中：引脚后缀A，B，C，D表示二阶滤波单元的组别；VIN为输入引脚；V1和V2为根据输入端VIN是接电阻还是电容表示不同的滤波响应输出。根据芯片手册，二阶单元内部元件R1=7 958 Ω，C=100 PF。当输入ZIN为电阻时，V1脚为带通响应输出，V2脚为低通响应输出端；当输入ZIN为电容时，V1脚为高通响应输出，V2脚为带通响应输出(LTC1562-2芯片二阶单元的内部等效电路见图2)。

在每个二阶单元中，中心频率f0，品质因素Q及增益HB均可通过外部电阻和电容，根据Linear公司给出的计算公式进行计算和设置。中心频率f0与品质因素Q的计算式分别为

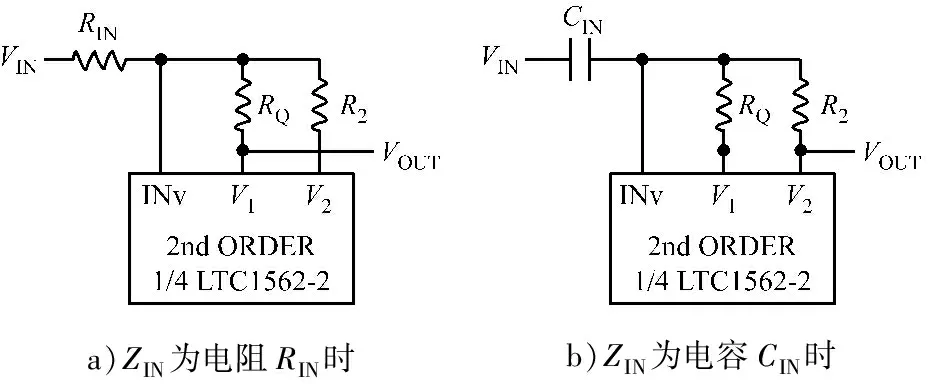
a)ZIN为电阻RIN时b)ZIN为电容CIN时

图3ZIN为电阻RIN或电容CIN时带通滤波器外部接线方法

(1)

(2)

R2，RQ和ZIN为二阶单元的外部元件，在设计带通滤波器时外部接线方式见图3。

ZIN为电阻RIN时，

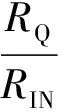
(3)

ZIN为电容CIN时，

(4)

式(1)～式(4)中:f0为中心频率,kHz;RQ,R2为外部元件,Ω;RIN为电阻,Ω;CIN为电容,PF。

2 基于LTC1562-2芯片的带通滤波器设计

在该接收机的设计中，为了使滤波器在通频带内的频率响应平坦、最大增益≈0dB、噪声小，在设计时采用巴特沃斯型的带通滤波器。带通滤波器中心频率为200(1±1%)kHz；-3dB带宽为20(1±10%)kHz；矩形系数≤5；滤波器阶数为8阶；滤波器类型为巴特沃斯型。

一般有源滤波器的设计过程是选择与目的相适应的滤波器，由必需的衰减量决定阶数，以二阶有源滤波器为单位，从归一化表中确定各级的中心频率和品质因素，再进行RC参数计算[3]。该方法在实际应用中过于繁琐，这里利用Linear公司的2个仿真设计软件FilterCAD及LTspice，并结合理论计算的方式实现上述滤波器参数的设计。设计步骤为：

1) 确定各二阶单元的中心频率f0和Q值。FilterCAD是一款滤波器设计软件，可根据滤波器的设计参数初步确定各二阶单元的f0和Q值，见图4和表1。

2) 根据式(1)和式(2)计算各二阶单元的R2和RQ值。

表1 f0和Q值的配置

表2 R2和RQ的计算值 kΩ

3) 用LTspice软件对上述参数进行仿真，并根据仿真曲线调整参数。

为了比较转移支付在中国教育水平趋同中的作用，下文将采用β绝对收敛、β条件收敛对中国以及东、中、西部地区间的教育水平进行研究，以揭示西部地区受教育水平差异及缩小的内在原因。中国各省的教育水平和转移支付都存在显著的空间效应，因此本文借助空间经济收敛模型，构建教育水平的空间β绝对收敛(式2～式3)和条件收敛的空间面板自相关模型和空间面板滞后模型(式4～式5)，以考察转移支付条件下教育水平增长与初期发展水平的关系。鉴于教育发展程度除了受国家财政支持力度的影响外，还取决于当地的经济发展水平，因此将经济发展水平也作为必要条件纳入β条件收敛模型。

在设计时根据实际情况ZIN选择电阻最为合适，有以下理由：

1) 滤波器的电路比较精密，外围元件很小的变化都会对其滤波效果产生很大的影响，而电容在精度上很难保证，且对于非常规的电容而言定制成本比较高，不适合用于滤波器设计；相反，电阻却可以购买到E96或E24系列的电阻值，该电阻值价格低、误差小且温度特性稳定。

2) 在LTC1562-2芯片手册中也明确“进行中心频率>200 kHz的滤波器设计中，ZIN采用电阻比较合适”。

仿真过程中，RIN的值根据式(3)来调整，除了保证滤波器最后一级输出满足设计要求以外，还要保证每级的输出最大增益尽可能在0 dB附近，防止输入波形增益过大，在时域特性上有失真的情况出现，可通过调整RQ和RIN的值来控制。

输入信号频率为200 kHz的正弦波，Vpp=40 mV，仿真滤波器电路仿真图见图5。图5中，外围电阻值均是根据仿真波形和计算公式调整后的参数。仿真各级频率响应曲线见图6～图9。

根据LTspice仿真软件调整后的最终外围电阻参数见表3。

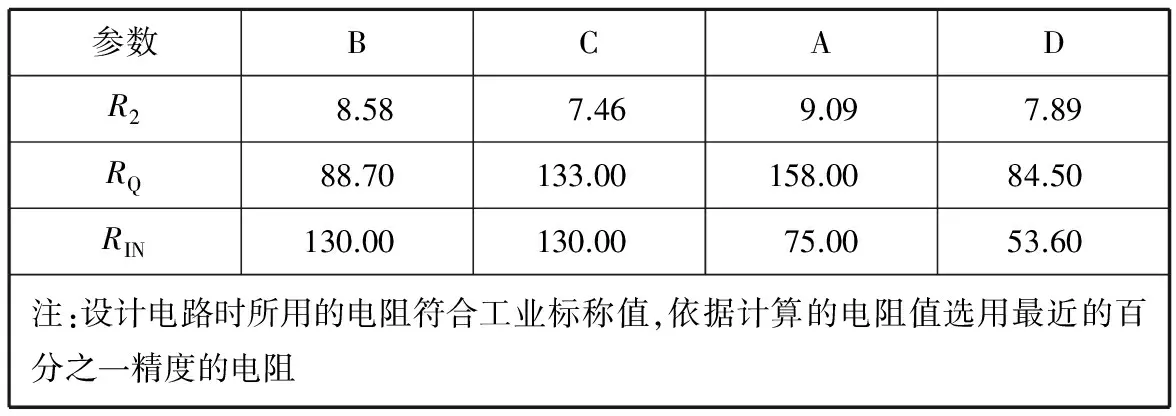
表3 可编程电阻值 kΩ

3 设计验证及电路测试

1) 由图9的仿真结果可计算出所设计滤波器的中心频率f0，-3 dB带宽B和矩形系数，均满足设计要求。

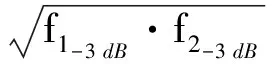
(5)

(6)

(7)

2) 根据表3各单元的RQ，RIN，R2值完成滤波器的制作。用信号源加入输入信号Vpp=20 mV，频率为200 kHz连续的正弦波。利用信号源和示波器测量其中心频率-3 dB带宽和-40 dB带宽，实测的中心频率略小，经过适当调整电阻后，滤波器所有指标均符合设计要求(测试参数见表4)。

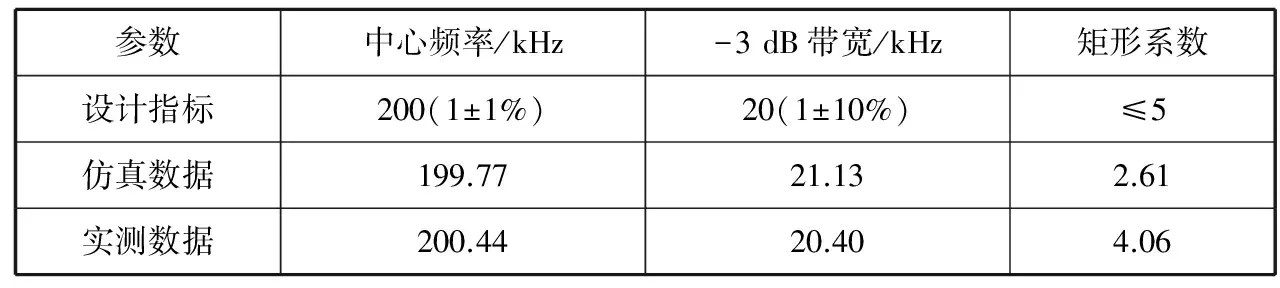
表4 实测参数与设计指标、仿真参数对比

3) 利用信号源加入频率为188～213 kHz的扫频信号，观察输出波形的平坦性(见图10和图11)。

由图10和图11可知，该输出波形在实际电路中的平坦性符合巴特沃斯型的滤波特性。

4 结 语

根据LTC1562-2滤波器芯片的技术指标，通过计算、仿真及实际电路测试证实，利用LTC1562-2芯片设计中心频率为200 kHz、-3 dB带宽为20 kHz的巴特沃斯型带通滤波器是可行的，并可满足某型声纳接收滤波电路的使用要求。

[1] 华成英.模拟电子技术基本教程[M].北京：清华大学出版社，2006.

[2] 冉茂华，陈三宝.基于LTC1562有源滤波器的设计与实现[J].中国有线电视,2005(19):1974-1976.

[3] 远坂俊昭，彭军.测量电子电路设计-滤波器篇[M].北京：科学出版社，2006.

ImprovedDesignofHighFrequencyBandpassFilterBasedonLTC1562-2

SHIChunhua
(Ship Automation Branch, Shanghai Ship & Shipping Research Institute, Shanghai 200135, China)

The performance of the filter in a Sonar Receiver directly affects the quality of the receiver signal. This paper introduces a sonar receiver filter constructed using LTC1562-2 filter chip instead of LTC1562 chip. The design process making use of Linear simulation software LTspiceIV and FilterCAD is presented. The Butterworth band-pass filter with a center frequency of 200 kHz is designed and tested.

band-pass filter； LTC1562-2； Butterworth； sonar

2017-04-10

石春华(1989—)，男，上海人，助理研究员，主要从事水声电子通信研究。

1674-5949(2017)02-0051-06

TN713

：A