基于Bass修正模型的即时通讯产品扩散研究

蒋亚萍+翁跃明

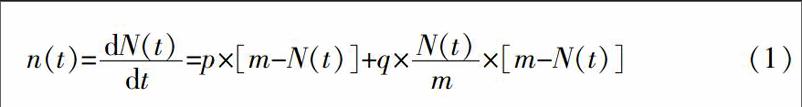
[摘 要] 分析了Bass基础模型存在的问题，引入负因子修正，运用非线性最小二乘法进行参数估计，建立了适用于即时通讯市场的新产品扩散模型，并对进一步的扩散研究进行了展望。

[关键词] Bass 模型；负因子修正；即时通讯市场；扩散

doi ： 10 . 3969 / j . issn . 1673 - 0194 . 2017. 11. 081

[中图分类号] TP311 [文献标识码] A [文章编号] 1673 - 0194（2017）11- 0164- 04

1 引 言

伴随着移动互联网的快速发展，即时通讯产品的特性及扩散分析成为了相当重要的研究课题。即时通讯软件具有显著的网络外部性，其网络外部性就是使用者越多，原有用户可以与更多人通讯，从而进一步带来效用的提高。当即时通讯网络中只有一个用户时，价值为零，而当网络中不断有用户加入后，通讯产品的价值则开始显现，人们可以通过即时通讯产品与他人沟通，实现信息的交流。这种用户间的交互衍生了即时通讯产品的协同价值，其本质就是网络外部性[1-5]。

随着创新扩散研究的深入，扩散模型的研究日益成为关注的焦点。1969年Bass模型的提出具有里程碑意义。Bass结合了Fourt和 Woodlock与Mansfield两种模型，认为创新产品的潜在采用者会受到大众媒体（外部影响）和口头传播（内部影响）的双重影响，其中受大众传媒影响的潜在采用者称为创新者，受口头传播影响的潜在采用者称为模仿者。鉴于此，Bass提出了综合外部影响和内部营销的模型—Bass模型。

Bass模型如下所示：

其中，n（t） 代表t时刻新产品采纳者数量；N（t）代表t时刻新产品采纳者累计总量，m代表潜在采纳者数量，p代表创新系数，表示尚未采纳产品的消费者在公共媒介传播影响下采纳该产品的可能性。q为模仿系数，表示潜在采纳者收到已采纳者影响而采纳该产品的可能性。

杨敬辉较为系统地介绍了使用Bass模型的常规分析过程及使用限制，并将参数估计的不同方法对扩散的估计的影响做了详尽的分析。董慧玲，李敏，赵维双，张彬等分别使用Bass模型对私人载客汽车、无缝技术、互联网等不同的市场进行了扩散过程分析。霍良安等根据经典Bass模型，从消费者个体角度出发，构建了基于用户体验的产品信息扩散模型。

2 基于负因子的Bass修正模型

3 實证分析

为了验证负因子修正模型对于即时通讯软件产品扩散分析的有效性，本文选取即时通讯软件扩散较为典型的微信作为实例分析对象。微信从2011年初开始推出第一个版本，到2016年第三季度用户数达到8.46亿，属于较为成功的扩散。为了完整分析扩散情况，取微信2011年-2016年之间的用户数据作为原始数据，数据时间间隔为3个月。

详细数据的表1所示。

在进行模型模拟之前，需要先对m、p、q、r进行参数估计。参数估计方法的选择是扩散模型创建能否成功的关键因素之一 ，典型参数估计方法有最小二乘法、极大似然估计法、非线性最小二乘法。

孟繁东对不同的参数估计做了较为详尽的对比分析，最小二乘法存在高估以及低估的情况，相对而言，非线性最小二乘法具有较为准确的估计结果。

本文利用SPSS中的非线性最小二乘法进行参数估计，设初值m（0）=5；p（0）=0.4；q（0）=0.1；r（0）=0.1，得到如下的参数估计值，见表2。

从结果来看，可获得以下结论：

（1）p

（2）r

（3）R2接近于1：说明本次的参数估计拟合结果非常好，能够反应实际用户情况；

（4）m 为11.344： 中国人口总数将近13亿，而微信的市场总体潜在用户数为11.344亿，说明微信用户人群将完全覆盖各年龄段用户，能够满足各年龄阶层的使用需求。

使用估计参数重新估算微信用户数见表3。

从图中可以得到以下分析结果：

（1）估算用户数与实际用户数基本吻合，能够作为预测结果；

（2）微信用户增长较快的时间周期是2012年至2018年前后，并将于2020年前后接近达到最大市场用户规模。

4 即时通讯产品扩散研究展望

随着移动互联网的快速发展，越来越多的即时通讯产品呈现在用户面前，诸如QQ、Skype、Jabber、微信、Whatsapp等各类软件进一步成熟，而类似于Ding Talk、Just talk的全新产品也在不断进入市场，运营商也在不断的上马融合通信软件，期望可以进入即时通信市场。因此，研究即时通讯产品市场的扩散，能够帮助企业预测产品的扩散情况，及时发现扩散中存在的问题，具有很好的指导作用。

Bass模型没有考虑用户流失过程，但在实际情况中，用户在选择该产品一段时间后，发现无法满足自身的使用需求后，会放弃使用该产品。如果需要考虑这个部分的情况，可以将Bass模型简单变换如下：

其中，r为流失系数，表示已采纳者的流失可能性。该微分方程为一阶非线性，无解析解，需要使用数值方法对该情况做进一步分析。同时，即时通讯市场后续将是多个产品竞争的扩散过程，在后续的研究中，可以进一步研究多产品的扩散竞争过程。

主要参考文献

[1]F M Bass. A New Product Growth Model for Consumer Durables[J]. Management Science，1969，15（5）：215 - 227.

[2]L A Fort， J W Woodlock. Early Prediction of Early Success of New Grocery Products[J]. Journal of Marketing， 1960，25（2）： 31-38.

[3]E Mansfield.Technical Change and the Rate of Imitation[J]. Econometrica， 1961，29（4）：741-766.

[4]杨敬辉.Bass模型及其两种扩展型的应用研究[D].大连： 大连理工大学，2005.

[5]董慧玲，介俊.基于 Bass 模型对中国私人载客汽车市场预测研究[J].北京工商大学学报：自然科学版，2007，25（4）：63-66.

[6]李敏，杨建梅，欧瑞秋.Bass 模型在无缝技术扩散中的应用及新发现[ J].科技管理研究，2007（7）：33 -36.