基于虚拟变量回归模型分析小区开放对周围道路通行的影响

梁 杰,陈 春，房 真,陈丹丹

(1.安徽财经大学金融学院，安徽 蚌埠 233030；2.安徽财经大学统计与应用数学学院，安徽 蚌埠 233030)

基于虚拟变量回归模型分析小区开放对周围道路通行的影响

梁 杰1,陈 春2，房 真2,陈丹丹2

(1.安徽财经大学金融学院，安徽 蚌埠 233030；2.安徽财经大学统计与应用数学学院，安徽 蚌埠 233030)

目的 针对小区开放问题，建立评价指标体系、车辆通行模型，对小区开放、道路通行影响进行定量研究。方法 以北京市某一区域交通情况为例，收集相关数据，使用虚拟变量、层次分析、多元线性回归、功效系数、控制变量等方法，分别建立虚拟变量回归模型、多元拟合回归模型、控制变量模型，综合运用MATLAB、EVIEWS等软件编程。结果 小区开放对周围道路通行影响与小区类型有关；车辆通行的模型为多元线性回归模型；住宅型小区开放对道路通行影响最大。结论 小区开放对道路通行可能有积极影响，也可能会有消极影响，城市规划研究单位和交通管理部门可以通过合理增加车道条数和交叉口个数，促进小区开放对道路通行的积极影响。

小区开放；虚拟变量回归模型；MATLAB；EVIEWS

2016年2月21日，国务院发布《关于进一步加强城市规划建设管理工作的若干意见》，其中第十六条关于推广街区制，原则上不再建设封闭住宅小区，已建成的住宅小区和单位大院要逐步开放等意见，引起了广泛的关注和讨论。近来，街区制成为热门话题，封闭式小区开放化主要是指原则上不再建设封闭住宅小区，已建成的住宅小区和单位大院要逐步打开，实现内部道路公共化。开放小区除了会带来安保问题，对周边道路通行也会产生一定程度的影响。本文试图从不同方面对小区开放对周边道路通行的影响进行定量研究，可以为城市规划和交通管理部门制定政策提供科学依据。

1 模型假设与名词解释

1.1 模型假设

不考虑除主干路、次干路、支路以外的小区周围道路类型；小区开放前后，小区附近的道路通行均被有效管理，交通秩序良好；小区周围道路车辆通行受行人因素的影响可忽略，且通行的机动车不包含大型货车；开放小区前后，小区周围的人口结构和建筑类型均不发生重大变化。

1.2 名词解释

道路饱和度是反映道路服务水平的重要指标之一。其计算公式为maxV/maxC,其中maxV为最大交通量，maxC为最大通行能力。路网密度是指城市范围内由不同等级、功能、区位的道路，以合适的形式和一定的密度组成的网络体系结构。

2 建立评价指标体系

2.1 研究思路

首先，找出某些影响因素，利用层次分析法对道路通行能力分层次进行分析。主要分为目标层、准则层、方案层3个层次[1]。其次，利用功效函数法将方案层的各个指标进行无量纲处理。然后，建立虚拟变量对小区开放与否以及交通流向平衡与否进行描述。最后，将层次分析得到的结果与建立的虚拟变量相结合利用功效系数法构造简单的虚拟变量的乘法方式回归，最终得到小区开放对周边道路通行的影响。评价被研究对象的综合状况，是指标无量纲化的一种方法。

2.2 研究方法

(1)层次分析法[2]

a.比较矩阵的建立

i)准则层：以交通服务水平、道路条件、交通状况3个因素做成对比矩阵，得到的比较判断矩阵为

ii)方案层：针对交通服务水平和道路条件的比较对比矩阵B1、B2为

针对交通状况的比较对比矩阵B3为

b.权重向量及一致性检验

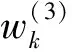
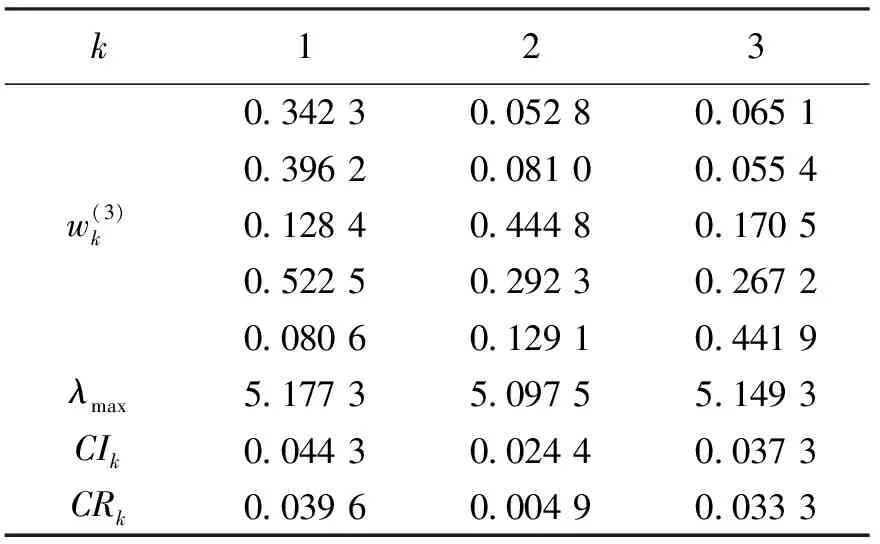
表1 方案层计算结果

由表1一致性检验数据可以看到3个一致性检验的比较判断矩阵的一致性全部都通过了检验。说明方案层的比较判别矩阵的建立也很合理。

由准则层的比较判别矩阵A计算出准则层对目标层的排序权值向量为

由一致性的方法步骤同样可以得到准则层的一致性比例CR=CI/RI=0.0092/0.58=0.0158<0.1，所以比较判别矩阵的一致性可以接受。

c.总目标的排序向量

(0.0921 0.1113 0.3185 0.2550 0.2232)T

层次总排序的一致性检验

所以层次总排序也通过了一致性检验。

(2)虚拟变量的设定

交通流向的设定[3]：理论上交通流向应该分为东、南、西、北4个流向，但是由于研究目标是道路通行能力，因此可以直接将交通流向设定为平衡与不平衡两类。其中

小区开放的设定：为研究小区开放对周边道路通行的影响，设定了小区开放的虚拟变量，将小区开放与否在一个表达式中表示出来，便于比较小区开放前后周边道路的变化情况。其中

(3)功效系数法无量纲各指标

考虑到层次分析中方案层的各指标量纲不相同，无法直接进行回归，因此利用功效系数法对各指标进行无量纲处理。因为功效函数中满意值和不允许值无法确定，所以以历史上最优值、最差值来分别替代满意值和不允许值。通过功效系数Ei(i=1,2,3,4,5)分别表示准则层的5个指标)直接消除量纲，将各个指标都化为量纲为1的指标，这样每个指标就可以直接相加减了。其中可以借助功效系数的思想通过每个指标减去该指标的历史最小值所得的差，再除以历史最大值，这样就可以便所有的指标量纲归一了。

功效系数的思想对各个指标处理后得到的新的指标分别为

2.3 结果分析

层次总排序的权重向量为W=(0.0921 0.1113 0.3185 0.2550 0.2232)T所以影响道路通行能力的5个主要指标饱和度、行程车速、路网密度、交通流向、行程延误对通行能力的影响系数分别为0.092 1、0.111 3、0.318 5、0.255 0、0.223 2。饱和度和行程延误对道路交通能力都是负影响，所以应该加上负号。

处理后的回归方程式为

小区开放后，会对部分基本变量造成影响，如会对道路总长度L、第i个车辆的行程时间ti、交通流量Di和通过路段极小时的自由流时间t0造成影响。为了比较小区开放的影响程度大小，设小区开放对造成影响的影响系数分别为λ1、λ2、λ3、λ4。

将小区开放虚拟变量的表达式代入处理后的回归方程式中，得到小区开放对周边道路通行能力的影响模型为

(1)

由此可以看出小区开放对周边道路的影响取决于影响系数λ1、λ2、λ3、λ4的大小与正负。影响系数又受到小区内部结构的影响，所以针对不同的小区类型，小区开放对周边道路通行能力的影响也不相同。

3 建立关于车辆通行的数学模型

3.1 研究思路

首先，以北京市某一区域交通情况为例，将单位时间内通过各个路段的车辆总数作为因变量，将影响车流量的主要因素作为自变量，并通过查询北京的交通运输网站等资料找到了12个路段车辆通行影响因素的有关数据[4]；其次，借助MATLAB软件将所查找到的数据进行无量纲化处理；然后，借助EVIEWS软件对数据进行回归分析与拟合，找出拟合度最优的模型，作为车辆通行的基本模型；最后，利用影子价格的思想研究小区开放造成的影响并得出结论。

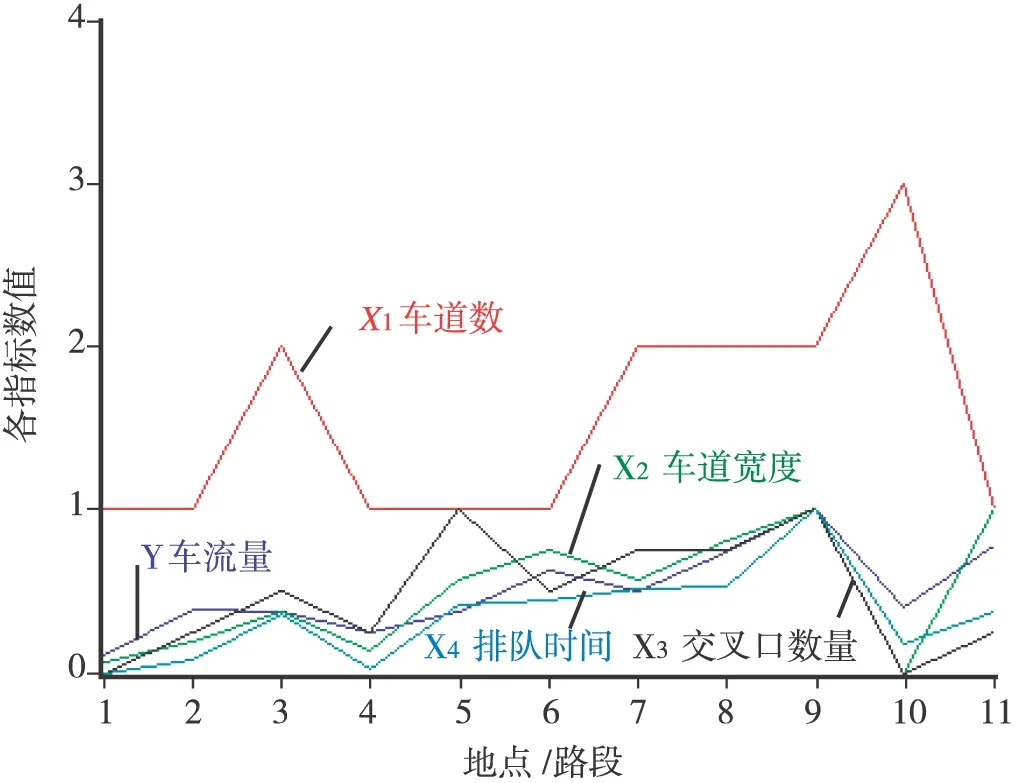
图1 自变量与因变量的变化趋势图

3.2 研究方法

借助EVIEWS软件分别作出处理后因变量yi与自变量x1i、x2i、x3i、x4i的变化趋势图(图1)。

由图1可以看出yi基本随着x1i、x2i、x3i、x4i的变化而变化，但是看不出来变化是呈线性还是非线性，为了了解因变量随自变量的具体变化形式，采取拟合回归的方法。

分别用EVIEWS软件求解，得到模型的结果及参数规范的形式如下：

a.多元线性回归模型

首先建立多元线性回归模型，得到的多元线性回归结果(图2)。

由图2可以列出多元线性回归模型的结果及参数

yi=0.1385+0.0478x1i+0.4776x2i-0.2878x3i-0.5348x4i

(0.1194)(0.06522)(0.1916)(0.1603)(0.3549)

t=(1.1595)(0.7330)(2.4933)(1.7956)(1.5068)

R2=0.9251F=18.5206n=11

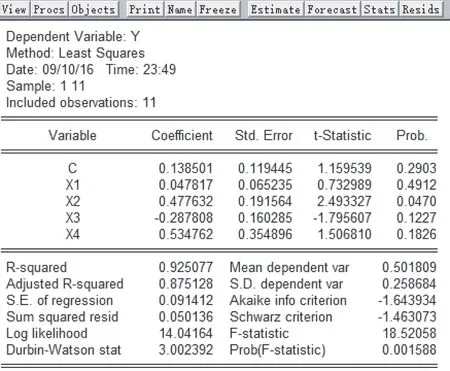
图2 多元线性回归结果

b.双对数回归模型

lnyi=-0.4920+0.2810lnx1i+0.6661lnx2i-0.2246lnx3i-0.0339lnx4i

(0.2359)(0.3411)(0.3945)(0.2673)(0.3235)

t=(2.0857)(0.8238)(1.6887)(0.8403)(0.1048)

R2=0.8439F=5.4081n=11

c.单对数模型

yi=0.6120+0.2098lnx1i+0.4523lnx2i-0.0699lnx3i-0.1191lnx4i

(0.1559)(0.2254)(0.2607)(0.1766)(0.2138)

t=(3.9248)(0.9307)(1.7345)(-0.3956)(0.5569)

R2=0.7673 F=3.2972 n=11

d.指数模型

lnyi=-2.0954+0.3615x1i+1.5898x2i-0.0049x3i-0.2361x4i

(0.4428)(0.2418)(0.7102)(0.5942)(1.3157)

t=(4.7321)(1.4949)(2.2386)(0.0084)(0.1794)

R2=0.8163 F=6.6636 n=11

由a、b、c、d这4种方法拟合得到的模型可以看出，多元线性回归模型拟合的最好、拟合度最高，所以车辆通行模型就选定为

yi=0.1385+0.0478x1i+0.4776x2i-0.2878x3i-0.5348x4i

(0.1194)(0.0652)(0.1916)(0.1603)(0.3549)

t=(1.1595)(0.7330)(2.4933)(1.7956)(1.5068)

R2=0.9251 F=18.5206 n=11

此时拟合度R2=0.9251，说明模型拟合的很好；F=18.5206也通过了F检验。由多元线性的回归系数可以看出车辆通行与车道、宽度成正比，与交叉路口数、排队时间成反比，符合实际意义。多元线性回归模型的误差分析如图3所示。

由图3可以看出拟合误差值在零的上下波动，且波动幅度不大，因此多元线性模型的拟合度很高。

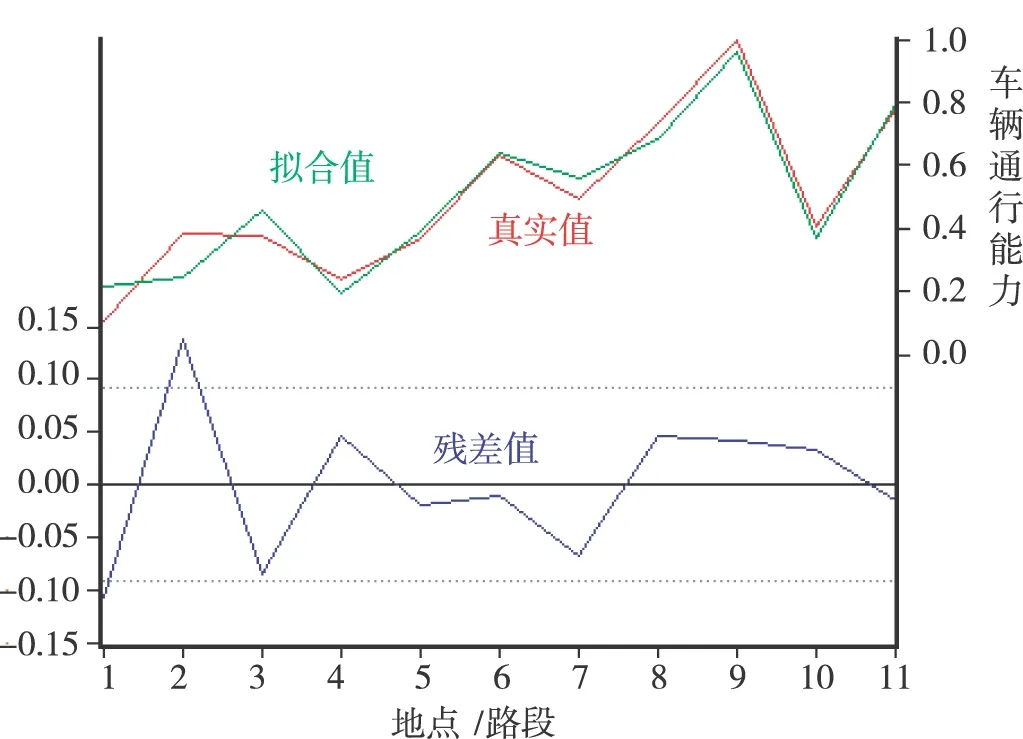
图3 多元线性回归分析图

3.3 结果分析

求得车辆通行模型为

yi= 0.1385+0.0478x1i+0.4776x2i

-0.2878x3i-0.5348x4i

(2)

由于小区开放后，会增加车道的条数及交叉路口的个数，也会影响排队时间，即小区开放会对x1、x3、x4造成影响。因为车道条数的增加对车辆通行的影响为积极的，而排队时间及交叉路口个数对车辆通行的影响是消极的。因此在判断小区开放对周边道路的影响时，要从多方面考虑。将积极影响与消极影响相比较，若积极影响条件更大，则小区开放改善了周边道路的交通情况；若消极影响大于积极影响，则小区开放不利于周边道路交通情况的改善[5]。

4 定量比较各种类型小区开放前后对道路通行的影响

4.1 研究思路

首先，前文提到了小区开放的4个影响系数λ1、λ2、λ3、λ4，在2.3节中主要利用层次分析法分析λ1、λ2、λ3、λ4的具体取值，便于下面的定量分析；其次，考虑车辆通行模型中因变量参与交通量的关系，在式(2)的基础上建立综合模型，综合考虑小区开放的影响；然后，根据车道条数、交叉路口数量、小区建筑密度将不同类型的小区进行分类并设定各个类型小区车道条数、交叉路口数量、小区密度的大小；最后，将设定好的各个类型小区车道条数、交叉路口数量、小区建筑密度的大小代入到综合模型中，比较并分析结果，得出结论。

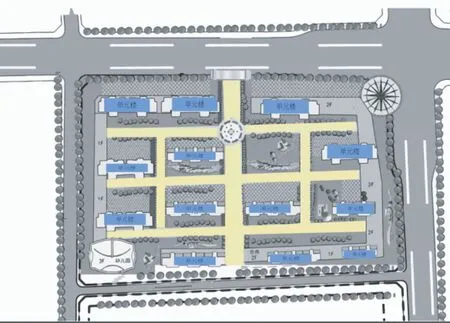
图4 小区平面图展现

4.2 研究方法

考虑到小区主要的区分在于车道的条数、交叉路口的个数以及小区的建筑密度上，所以主要根据这3种影响因素将小区分为住宅型小区、教育型小区以及商业型小区。划分依据就是住宅型小区面积最小，车道条数和建筑物密度大，交叉路口多；商业型小区面积最大，车道条数、交叉路口最少，建筑物密度最小；教育型小区处于中间位置[6]。本文创建的小区类型平面图大体见图4。不同类型的小区主要是3个影响因素的不同。

通过对周边小区的调查以及网上查找资料，不同类型小区的主要划分界限见表2。

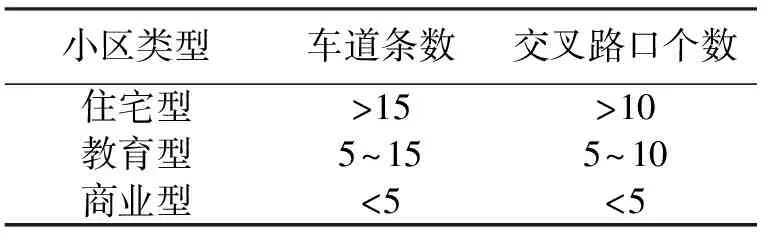
表2 小区的划分界限

利用层次分析法确定小区开放后对道路总长度L、第i个车辆的行程时间ti、交通流向Di和通过路段极小时的自由流时间t0的影响系数λ1、λ2、λ3、λ4的大小。以小区开放的影响程度为准则，对道路总长度L、第i个车辆的行程时间ti、交通流量Di和通过路段极小时的自由流时间t04个因素进行成对比较，得到比较判别矩阵

借助MATLAB求解得到4个因素的权重向量为W=(0.5462，0.2323，0.0838，0.1377)

一致性比例CR=CI/RI=0.017/0.9=0.0189<0.1，因此比较判别矩阵的一致性可以接受，所以求得的权重向量也可以接受。所以

(λ1,λ2,λ3,λ4)=(0.5462,0.2323,0.0838,0.1377)

可以直接将λ1、λ2、λ3、λ4的具体数值代入到公式(1)中，又因为小区开放会增加道路总长度L，减小第i个车辆的行程时间ti及通过路段极小时的自由流时间t0，对交通流向Di也是负影响，因此λ1前面的系数是正的，λ2、λ3、λ4前面的系数是负的。

②综合模型的建立

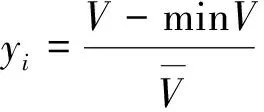
由上述公式可得到V=927.8+61.71x1i+616.58x2i-371.55x3i-690.43x4i，综合可得模型：

0.2550Di(1-0.0838Ti)-0.2232×

4.3 结果分析

由于本文研究的是定量比较各种类型小区开放前后对道路通行的影响，所以采取控制变量法将与小区类型无关的变量都控制一致，与小区类型紧密相关的数据按照小区类型的划分界限取值分别代入，这里，将x1i、x3i定为变量，其他的都定为定量(交通流向即Di=1都设为恒定)。然后对3种类型小区所得结果进行分析。

①住宅型小区

a.小区开放，即Ti=1时，令x1=16,x3=11，求得结果Y=65.40；

b.小区不开放，即Ti=0时，令x1=16,x3=11，求得结果Y=75.56。

②教育型小区

a.小区开放，即Ti=1时，令x1=7,x3=7，求得结果Y=46.57；

b.小区不开放，即Ti=0时，令x1=7,x3=7，求得结果Y=32.15。

③商业性小区

a.小区开放，即Ti=1时，令x1=3,x3=3，求得结果Y=13.28；

b.小区不开放，即Ti=0时，令xi=3，x3=3,求得结果Y=2.8995。

5 结 论

本文利用虚拟变量回归模型，设置虚拟变量，利用封闭小区的数据巧妙地对小区开放后的状况进行分析，客观地分析出开放小区对道路通行的影响，体现了灵活性特点。运用层次分析法建立模型，就开放小区道路通行状况，选取主要影响因素，有条理地进行分层分析，使得到的结果更清晰。使用多元线性回归模型、双对数回归模型、单对数模型及指数模型分别对数据进行拟合，再筛选出拟合效果最优的模型，根据该模型能准确地分析开放小区对车辆通行的影响。

此外，本文所建立的虚拟变量回归模型，还适用于引入虚拟变量作为表现定性因素的变量分析如性别、种族、职业、季节、文化程度、政府经济政策的变动等问题。

[1]杨桂元，朱家明.数学建模竞赛优秀论文评析[M].合肥：中国科学技术大学出版社，2014：10.

[2]杨桂元.数学建模[M].合肥：中国科学技术大学出版社，2014：8-56.

[3]庞皓.计量经济学[M].北京：科学出版社，2014：6-72.

[4]王晋.推广街区制对城市路网布局的影响及对策[J].城市道桥与防洪,2016(06):4-10.

[5]李向朋.城市交通拥堵对策：封闭型小区交通开放研究[D].长沙：长沙理工大学，2014，5.

[6]郑俊飞,张笑荷,张风超.中国社区矫正工作中存在的问题与完善途径[J].河北北方学院学报(社会科学版),2016(04):86-89.

[责任编辑：关金玉 英文编辑：刘彦哲]

Analysis of Influence of Community Opening on Surrounding Traffic Based on Virtual Variable Regression

LIANG Jie1,CHEN Chun2,FANG Zhen2,CHEN Dan-dan2

(1. School of Finance,Anhui Finance & Economics University,Bengbu,Anhui 233030,China; 2.School of Statistics and Applied Mathematics,Anhui Finance & Economics University,Bengbu,Anhui 233030,China)

Objective In view of community opening,to establish the evaluation index system,traffic model and quantitatively analyze the influences of community opening on surrounding traffic.Methods By taking the traffic of an area in Beijing as an example,after collecting relevant data,the virtual variables,hierarchical analysis,multiple linear regression,efficacy coefficient and control variables were used to respectively set up virtual variable regression model,the fitting of multivariate regression model and the control variable model.And programming softwares such as MATLAB and EVIEWS,were also used.Results the study showed that the influence of community opening on the surrounding road traffic was related to the area type;the vehicle traffic was of a multiple linear regression model;and the residential area opening had the greatest impact on surrounding traffic.Conclusion Community opening may have a positive or negative influence on traffic.Therefore,the urban planning and traffic management departments should reasonably increase the number of lanes and crossings,so as to promote the positive influence of the community opening on traffic.

community opening;virtual variable regression model;MATLAB;EVIEWS

国家自然科学基金项目(11601001)

梁杰(1996-)，女，安徽灵璧人，安徽财经大学金融学院在读学生，研究方向：金融工程。

F 572.88

A

10.3969/j.issn.1673-1492.2017.07.006

来稿日期：2016-11-16