圆锥曲线重要考点分析

■河南省平顶山市第一中学 胡 玉 王丽娜

圆锥曲线重要考点分析

■河南省平顶山市第一中学 胡 玉 王丽娜

圆锥曲线问题一般是以直线和圆锥曲线的位置关系为载体,以参数处理为核心,需要综合运用函数与方程、不等式、平面向量等诸多知识,以及数形结合、分类讨论等多种数学思想方法进行求解,对考生的代数恒等变形能力、计算能力等有较高的要求。

考点1——圆锥曲线中的定点、定值问题

定点、定值问题是解析几何解答题的考查重点。此类问题定中有动,动中有定,并且常与轨迹问题、曲线系问题等相结合,深入考查直线与圆锥曲线的位置关系等知识。

(1)求椭圆C的方程;

(2)如图1所示,A、B、D是椭圆C的顶点,P是椭圆C上除顶点外的任意一点,直线DP交x轴于点N,直线AD交BP的延长线于点M,设BP的斜率为k,MN的斜率为m,证明:2m-k为定值。

思路点拨：(1)根据a,b,c的关系求出a,b的值;(2)设出直线BP的斜率k,得到直线BP的方程,结合椭圆的方程求出点P的坐标,联立直线AD和BP的方程解得点M的坐标,根据D、P、N三点共线得到点N的坐标,求出直线MN的斜率后代入所求的式子即可解得答案。

图1

点评:在解决圆锥曲线中的定点、定值问题时,可以先研究一下特殊情况,找出定点或定值,再视具体情况进行研究。同时,也要掌握巧妙利用特殊值解决相关的定值、定点问题的选择题或填空题,如将过焦点的弦特殊化,变成垂直于对称轴的弦来研究等。

考点2——圆锥曲线中的最值、范围问题

已知抛物线C的顶点为O(0, 0),焦点为F(0,1)。

(1)求抛物线C的方程;

(2)如图2,过点F作直线交抛物线C于A、B两点,若直线AO、BO分别交直线l:y=x-2于M、N两点,求|MN|的最小值。

思路点拨：(1)根据条件和抛物线的标准方程,可直接求出;(2)根据直线方程及抛物线方程写出MN长度的解析式,再根据求出的解析式选择适当的方法求最值。

解析：(1)由题意可设抛物线C的方程为x2=2py(p〉0),则=1,所以抛物线C的方程为x2=4y。

(2)设A(x1,y1),B(x2,y2),直线AB的方程为y=kx+1。

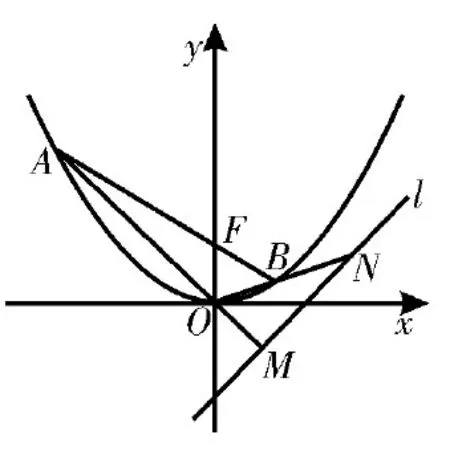
图2

点评:求最值或范围问题时常见的解法: (1)几何法,若题目中的条件和结论能明显体现几何特征及意义,可考虑利用图形性质来解决;(2)代数法,若题目中的条件和结论能体现一种明确的函数关系,则可首先建立目标函数,再求最值。

考点3——圆锥曲线中的存在性问题

存在性问题属于探索性问题的范畴,是近几年高考的热点题型,主要探索是否存在满足某些条件的点、直线或数值等。

图3

(1)求椭圆C的方程。

(2)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA、PB、PM的斜率分别为k1、k2、k3,问:是否存在常数λ,使得k1+k2=λk3?若存在,求出λ的值;若不存在,请说明理由。

思路点拨：(1)由点在椭圆上和离心率建立方程组求出椭圆的方程。(2)设出直线的方程,将其与椭圆的方程结合得到一个一元二次方程,根据根与系数的关系得出A、B两点坐标之间的关系和点M的坐标,由此得出相应直线的斜率,根据A、F、B三点共线得出相应坐标之间的关系,从而求出常数的值。

依题设知a=2c,则b2=3c2。 ②

将②代入①,解得c2=1,a2=4,b2=3。

故椭圆C的方程为+=1。

(2)由题意可设AB的斜率为k,则直线AB的方程为y=k(x-1)。 ③

代入椭圆方程3x2+4y2=12,整理得(4k2+3)x2-8k2x+4(k2-3)=0。

点评:(1)解决存在性问题的关注点。求解存在性问题,先假设存在,推证满足条件的结论,若结论正确,则存在;若结论不正确,则不存在。①当条件和结论不唯一时要分类讨论。②当给出结论而要推导出存在的条件时,先假设成立,再推出条件。

(2)存在性问题的解题步骤,如图4。

图4

强化训练 设P是圆x2+y2=4上的任意一点,由点P向x轴作垂线PP0,垂足为P,且=。

(1)求点M的轨迹C的方程。

(2)设直线l:y=kx+m(m≠0)与(1)中的轨迹C交于不同的两点A、B。若直线OA、AB、OB的斜率成等比数列,求实数m的取值范围。

解析：(1)设点M(x,y),P(x0,y0),由题意知P0(x0,0)。

(责任编辑 王福华)