坡面径流实时监测装置的测试与率定

李智广, 曹文华, 牛勇

(1.水利部水土保持监测中心，100053，北京；2.山东农业大学，271018，泰安)

坡面径流实时监测装置的测试与率定

李智广1†, 曹文华1, 牛勇2

(1.水利部水土保持监测中心，100053，北京；2.山东农业大学，271018，泰安)

径流小区观测技术是水土保持监测评价的基础。研发适用于径流小区尺度的径流观测装备可有效减少人工监测的随机性，降低监测人员的工作强度。通过人工模拟不同强度的产流汇水条件，对“径流泥沙含量实时测量装置”开展径流测量性能的专项测试，结果表明：该装置在测试环境条件下的径流测量相对误差范围为-4.33%～-24.01%，稳定时长范围为55～130 s。偏相关分析发现：测量稳定时长与径流的含沙量、流量分别呈显著正相关关系和显著负相关关系(P<0.05)；测量精度与含沙量和流量的相关系数均呈负相关关系，但含沙量和流量对测量精度的影响有限(α=0.05)。通过回归分析，得到该装置径流量修正模型；经验证，该模型可使平均相对误差由修正前的11.53%降低至6.80%，平均测量数据稳定时间由修正前的96 s降低至80 s。研究分析提出，通过对上述设备增设波浪过滤消减装置、增大滤波管直径等措施可进一步降低测量误差，提高工作稳定性。基于上述测试结果，本研究认为通过利用修正模型，测试设备的径流测量效果在测试流量范围内较为理想，即该设备在降雨强度范围为3.60～66.96 mm/h的产流工作条件下较为适宜。

径流小区观测； 径流量； 测量精度； 修正模型； 偏相关分析

径流是生态系统水量平衡的重要输出项[1]，也是产生地表水蚀的动力来源。径流总量、径流过程是反映坡面尺度地表径流重要指标[2]，也是侵蚀模型参数率定的根本依据[3-4]。随着水土流失研究和水土保持监管工作的不断发展，我国目前已建立由738处水土保持监测站点组成的监测站网体系(含290余处坡面径流观测场，2 600余个径流小区)[5-6]，用于不同地区长期开展坡面径流观测，此外在我国还存在众多由科研院校运管的坡面径流观测设施。坡面径流小区径流观测不同于小流域水文站径流观测，其特点是径流总量小、径流过程快。为满足坡面径流小区径流观测的需要，目前常用的径流观测设施(设备)有集水箱、多级分水桶(池)、基于水位转换的测流槽及翻斗流量计等。由于测量原理和设备精度的限制，上述常用设施(设备)在使用时均存在一定的局限性：集水箱和分水桶(池)测量工作以人力为主，自动化程度低；测流槽对于流量和水位计精度要求较高，观测小流量径流难度大；翻斗式流量计在大径流条件下易产生系统性的漏测[7-10]。因此探索其他工作原理的坡面径流测量装置[11-13]，可以作为现有坡面径流测量技术体系的有益补充，并有利于提升我国水土流失的监测水平。此外，探索构建针对水土保持专用设施设备的检测方法与技术规程，对提升我国整体水土流失监控能力具有重要意义。

2014年，长春工程学院和吉林省水土保持科学研究院联合申报了一种名为“径流泥沙含量实时测量装置及测量方法”(201410426952.X)的发明专利。为满足不断扩大的小区尺度径流自动测量装备需求，提升我国水土保持监测装备水平，水利部水土保持监测中心在2015年委托中国科学院水利部水土保持研究所对该装置的径流测量功能进行了专项测试。

笔者基于测试数据与分析，对该装备的性能和适用性进行了评价，以期相关分析结果能够有助于水土保持监测装备的选型及相关工作能力的提升，并有助于形成水土保持监测专用设备的检测技术体系完善与发展，推动水土保持监测设备专用设备研发、生产行业的规范化、标准化发展，以适应当前水土保持监测工作的发展趋势。

1 装置结构及工作原理

该装置由测量机械部件(1测量桶、2下支架、3称量传感器、4放水管、5电动阀等)、控制部件(9控制器)、处理器(10处理器)等3部分组成(图1)。其中：机械部件是该装置的核心部件，用于直接测量径流和泥沙含量；控制部件用于接收液位传感器和称量传感器数据，控制电动阀启闭，并向处理器发送采集的数据；处理器用于数据输出。

该装置的具体工作原理为：径流小区收集的径流进入测量桶，桶底电动阀处于关闭状态，液位传感器实时监测桶内水位，当随着测量桶收集的径流量增加至设定的最高水位Hh时，称量传感器测定此时桶体及进入内部的径流重量W1，同时，桶底电动阀打开，桶内水量外泄，液面降低，当液面降低至设定的最低水位Hl时，桶底电动阀5闭合，称量传感器测定此时桶体及内部水体的重量W2，至此一个测量循环完成，依次连续循环测量，完成一场降雨带来的汇流量测量。径流过程由处理器输出、存储。

径流总量Qm的计算公式为

(1)

式中：Qm为设备测量记录得到的径流量，m3；S为测量桶底面积，m2；Hh为测量筒设定最高液位，m；Hl为测量筒设定最低液位，m；Hc为本次径流结束时留在桶内的液面高度，m；t为本次径流过程总用时，s；t1为开阀时间，指从电动阀开始启动至完全开启所需时间，s；t2为关阀时间，指从电动阀开始启动至完全关闭所需时间，s；t3为放水时间，指从电动阀完全开启放水至电动阀开始关闭结束放水所需时间，s。

1.测量桶Measuring bucket ；2.下支架Low holder；3.称量传感器Weighing sensor；4.放水管Offlet；5.电动阀Electric valve；6. 上支架Upper holder；7.液位传感器Water level sensor；8.滤波管Waves filter；9.控制器Controller；10.处理器Processor；11.外翻边Flanging；12.残留浑水Residual water； Hh: the highest water level; Hc: the water level when the runoff was finished. Hl: the lowest water level.图1 径流泥沙含量实时测量装置整体结构图Fig.1 Structure of a Runoff and Sediment Real-time Measuring Device

2 测试方法

通过流量控制装置向测量桶内注入一定流量的水流，模拟坡面产流过程，通过对比、分析装置实测流量数据与理论流量(注入水量)间的差异，判定装置的测量性能。此外，本次测试设置无沙径流和有沙径流作为测试水样，探讨不同含沙比例条件对供试装置影响，即2因素多水平控制性测试，每项试验设计重复3次。具体的控制因素、水平设置如表1所示。

表1 测试处理设置Tab.1 Treatments of test

注：为避免含沙量水样制作误差，在测试时，采用“设计掺沙量”代替“径流含沙量”。Note: In order to avoid the error of flow sample, the runoff sand content was replaced by design sand addition in this study.

供试流体储存于储水箱内，箱体内供试流体通过安装在底部的潜水泵和输水管道向装置的测量筒输水，利用安装在管道上的流量传感器、PID控制器和变频器调节、稳定流量，在水泵启动时要关闭出口阀门，运行到一定转速后再打开阀门，进行测试。供试流体带沙测试时，在测试开始前先向储水箱内加入定量泥沙(取自径流观测场，烘干状态)，测试时注入清水，代表含沙径流。无沙小流量条件下单次测试时长约为2 min，流量设置为0.1和0.5 L/s；无沙大流量条件下单次测试时长约为80 s，流量设置为0.91、1.6和1.86 L/s。在带沙测试中，单次测试时间相应延长，一般取140 s。测试期间测试区域空气温度范围为21～25 ℃。

装置测量径流量Qm由电脑处理器输出，理论径

流量Qs由设置流量和测试时间计算得到。本文采用相对误差判断装置测量精度，计算公式如下：

(2)

式中：δ为设备测量相对误差，%；Qm为设备测量记录得到的径流量，m3；Qs测试系统提供的径流量，m3。

3 结果与分析

3.1 径流量测量及其误差

图2 无沙、不同流量条件下测试结果Fig.2 Result of test under different conditions without sand in tested water

1)无沙、不同流量条件下测试结果。如图2(a)所示，在无沙、流量为0.1 L/s条件下，径流量测量值随着时间的增加，越来越接近理论值，即测量误差在逐渐降低，在第110秒左右，相对误差开始稳定在-12.20%±2.92%左右。此外，可以由图3(a)发现，该条件下，测量结果均小于理论值，即在该测量结构条件下测量结果存在系统性的偏小。如图2(b)所示，在无沙、流量为0.5 L/s条件下，测量误差同样随着时间的增加，越来越降低，在第80秒左右，相对误差开始稳定在-11.45%±3.22%左右。该条件下，测量结果同样整体小于理论值。如图2(c)所示，在无沙、流量为0.91 L/s条件下，相对误差在第70秒左右开始稳定在-18.64%±7.83%左右，该条件下，测量值仍整体小于理论值。如图2(d)所示，在无沙、流量为1.6 L/s条件下，径流量测量相对误差在第60秒左右稳定在-18.64%±7.81%左右，系统误差略大于前3组实验，通过分析系统采集数据发现，3组重复实验中仅有一组实验误差值较大，说明这组数据可能受到外部因素影响，导致误差平均值略大。如图2(e)所示，在无沙、流量为1.86 L/s条件下，实验开始后测量误差在逐渐降低，在第55秒左右，相对误差开始稳定在-4.33%±0.08%左右，相较于其他4组不带沙试验，在流量为1.86 L/s条件下的相对误差最小，而且设备的稳定时间最短。通过整体对比分析发现，在不带沙测试条件下，设备测量稳定时间随着设定流量的增加而减少。

2)不同掺沙量、流量条件下测试结果，如图3所示，在流量为0.5 L/s、掺沙量分别为1、3和5 kg条件下，相对误差达到稳定的时长分别为110、120和130 s，稳定的相对误差分别为-11.59%±0.10%、-24.01%±9.19%、-7.42%±1.51%，对比可以发现，随着掺沙量的增加，相对误差达到稳定的时长随之增加，即测试水流中的泥沙阻碍了设备测试结果的稳定。相较于流量为0.5 L/s的不掺沙测试(T2处理)，掺沙试验径流量相对误差达到稳定的时长显著大于不掺沙试验(80 s，P<0.01)。

在流量为0.91 L/s、掺沙量分别为1、3、5和10 kg条件下，相对误差达到稳定的时长分别为80、110、120和110 s，稳定的相对误差分别为-10.12%±4.62%、-7.19%±4.52%、-11.59%±2.75%、-11.53%±5.91%，对比可以发现，随着掺沙量的增加，相对误差达到稳定的时长整体随之增加。

图3 不同掺沙量、流量条件下测试结果Fig.3 Result of test under different flow and sand addition in tested water

3.2 径流量测量的影响因素分析

为分析径流量、掺沙量对精度和测量稳定时长的影响，笔者对上述测试结果进行偏相关分析。如表2所示，在精度作为控制变量的条件下，稳定时长与掺沙量和流量分别呈正相关关系和负相关关系(相关系数分别为0.617、-0.718)，且均显著相关(P<0.05)。在稳定时长为控制变量的条件下，测量精度与掺沙量和流量的相关系数均呈负相关关

系，但掺沙量和流量对测量精度的影响有限(α=0.05)。此外分析发现，相较于流量为0.91 L/s的不掺沙测试(T3处理)，掺沙试验径流量相对误差达到稳定的时长显著大于不掺沙试验(70 s，P<0.05)。通过对比不同流量条件下的掺沙试验结果，小流量(0.5 L/s)条件下的测量数据稳定时间要显著大于大流量(0.91 L/s)条件下的时长(P<0.05)，但测量精度无显著性差异(P>0.05)。

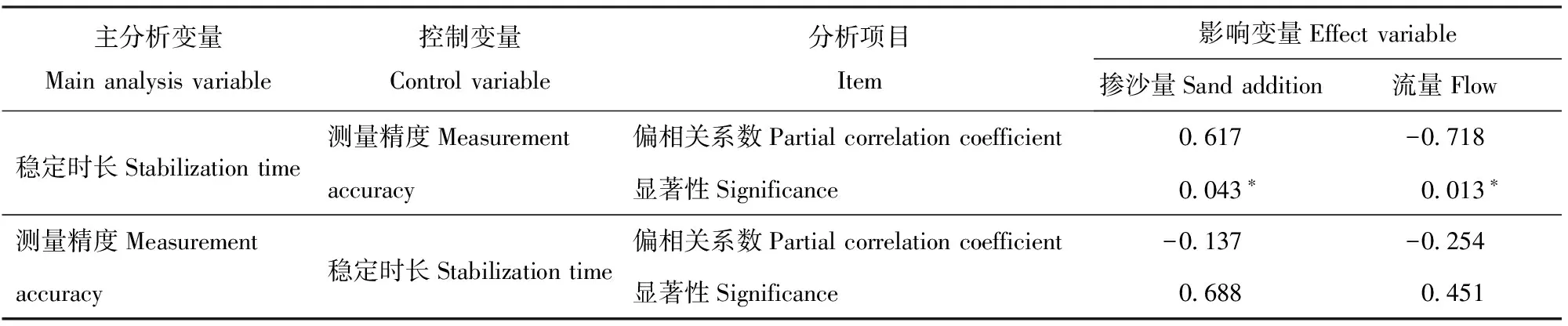
表2 偏相关分析结果Tab.2 Analysis of partial correlation

注：“*”表示在显著水平为0.05的条件下显著相关。Note:* indicated that correlation was significant atP<0.05.

3.3 测量参数率定

由上述测试结果可知，该装置直接测量得到的径流量测量值Qm与理论值Qs之间存在较好的相关性，因此可以通过回归的方法建立测量修正模型，将率定出的模型参数输入装置的处理器，以达到提升装置测量精度的目的。模型构建时以T1、T3、T5、TS1、TS3、TS4、TS6处理的测试结果作为率定数据，其流量、掺沙量范围基本可以覆盖测试实验设计；以T2、T4、TS2、TS5、TS7处理的测量数据作为修正模型的验证数据。

如图4所示，基于径流量测量值与和理论值，构建本装置径流量的修正模型(式3)，决定系数达到0.99，拟合精度较高。采用获得的修正模型，T2、T4、TS2、TS5、TS7处理的测量数据作为修正模型的验证数据，验证修正模型对测量数据的修正效果。如图5所示，通过模型修正，5组验证数据在修正后的平均相对误差可由修正前的11.53%降低为6.80%，平均测量数据稳定时间可由修正前的96 s降低为80 s，即修正模型起到较好的修正作用。

图4 径流量修正值与测量值拟合结果Fig.4 Fitted curve of runoff

图5 修正模型验证结果Fig.5 Validation result of modified model

(3)

式中QM为通过修正模型得到的径流量，m3。

4 结论与讨论

1)通过测试发现，本次测试的装置在不同测试工况条件下测量相对误差范围为-4.33%～-24.01%，稳定时长范围为55～130 s，测量精度和稳定时长主要受流量影响，但设备的测量值存在较明显的系统性偏差，即测量数据较理论值整体偏小。由径流总量QT的计算公式(式1)可知，径流总量QT测量值的大小仅与测量桶内液位高度的测量值有关，准确地说是由于设定的最高水位与最低水位的差值(Hh-Hl)整体偏小导致测量值系统性偏小。由于在径流量的测量过程中液位高度则是通过超声波水位计(液位传感器)获得的，在该过程中超声波水位计的工作环境变化(温、湿度)较小，即可排除超声波水位计自身的测量偏差。因此可能导致系统性偏差的原因可归结为2类：一类是不同水深条件下水面波动差异所导致(Hh-Hl)整体偏小；另一类是不同水深条件下的超声波投影变化导致液位测量偏差[14-17]。针对这2种可能的原因，笔者提出可通过增设波浪过滤消减装置、增大滤波管直径等措施来降低测量误差。

2)通过修正模型验证可以发现，虽然修正模型对径流量的测量整体修正效果较好，但对于大流量、含沙量的条件下，修正模型的修正作用比较有限；因此可以通过继续开展大流量、含沙量条件下设备测试工作，积累相关数据，构建适用于该工况条件下的修正模型，以提高设备测量精度。

3)本次测试的流量范围为0.1～1.86 L/s，按照标准小区面积(100 m2)和北京地区土石山区林地径流系数(0.031 5)折算降雨强度，流量范围对应的降雨强度范围为3.60～66.96 mm/h，降雨强度可覆盖中雨至暴雨量级。

4)由于掺沙量对精度影响不显著，因此在试验流量范围内的含砂水平均可被该设备较好的测得。

基于上述研究及讨论，建议今后可开展更为深入的含沙量、泥沙机械组成对设备的影响分析，方便水土保持监测工作者高效开展径流监测。此外，我国水土保持监测工作信息化处于起步升级阶段，大量专用水土保持监测设备大量开发、推广，急需与这类设备相配套的检测方法与技术规程，以有助于该行业的向规划化、标准化发展。

[1] BRACKEN L J, KIRKBY M J. Differences in hillslope runoff and sediment transport rates within two semi-arid catchments in southeast Spain[J]. Geomorphology, 2005,68(3/4):183.

[2] CAREY S, WOO M. Slope runoff processes and flow generation in a subarctic, subalpine catchment[J]. Journal of Hydrology, 2001,253(1/2/3/4):110.

[3] 黄俊，金平伟，李敏，等. 径流小区尺度土壤入渗率影响因子与估算模型[J]. 农业机械学报, 2016, 47(8):171. HUANG Jun, JIN Pingwei, LI Min, et al. Influencing factors of soil infiltration rate and its estimation model at runoff-plot scale[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(8):171.

[4] PARSONS A J, BRAZIER R E, WAINWRIGHT J, et al. Scale relationships in hillslope runoff and erosion[J]. Earth Surface Processes and Land forms, 2006,31(11):1384.

[5] 赵院，马力刚. 浅析全国水土保持监测站网布设方案[J]. 中国水土保持, 2016(1):23. ZHAO Yuan, MA Ligang. Analyses on the scheme of laying of nationwide water and soil loss monitoring network[J]. Soil and Water Conservation in China, 2016(1):23.

[6] 姜德文，中国水土保持监测站点布局研究[J]. 水土保持通报, 2008,28(5):1. JIANG Dewen. Distribution of soil and water conservation monitoring stations in China[J]. Bulletin of Soil and Water Conservation, 2008,28(5):1.

[7] 赵军，屈丽琴，赵晓芬，等. 称重式坡面径流小区水流流量自动测量系统[J]. 农业工程学报, 2007,23(3):36. ZHAO Jun, QU Liqin, ZHAO Xiaofen, et al. Automated weighting system for measuring flow rate from runoff plots [J].Transactions of the CSAE, 2007,23(3): 36.

[8] 符素华，付金生，王晓岚，等. 径流小区集流桶含沙量测量方法研究[J]. 水土保持通报, 2003,23(6):39. FU Suhua, FU Jinsheng, WANG Xiaolan, et al. Sediment content measurement in collecting tanks of runoff plots[J]. Bulletin of Soil and Water Conservation, 2003, 23(6):39.

[9] 谢颂华，方少文，王农. 水土保持试验径流小区设计探讨[J]. 人民长江, 2013,44(17):83, 113. XIE Songhua, FANG Shaowen, WANG Nong. Discussion on design of runoff plot in soil and water conservation experiment[J]. Yangtze river, 2013,44(17):83.

[10] 曹建生，张万军，刘昌明. 一种斜拉翻斗式自记流量测定仪[J]. 水利水电技术, 2005,36(1):28. CAO Jiansheng, ZHANG Wanjun, LIU Changming. A diagonal pull tipping-bucket self-recording flow meter[J]. Water Resources and Hydropower Engineering, 2005,36(1):28.

[11] 王辉，雷廷武，赵军，等. 坡面径流量与含沙量动态测量系统[J]. 农业机械学报, 2005,36(1):79. WANG Hui, LEI Tingwu, ZHAO Jun, et al. System for dynamic measurements of hillslope runoff rate and sediment concentration[J]. Transactions of the Chinese Society for Agricultural Machinery, 2005,36(1):79.

[12] 董月群，庄晓晖，雷廷武，等.电解质脉冲边界模型测量冻土坡面径流流速距离优选[J]. 农业机械学报, 2015, 46(2):146. DONG Yuequn, ZHUANG Xiaohui, LEI Tingwu, et al. Optimum measurement distance of water flow velocity over frozen slopes with pulse boundary model method[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(2):146.

[13] 雷廷武，张宜清，赵军，等. 近红外反射高含量泥沙传感器研制[J]. 农业工程学报，2013，29(7):51. LEI Tingwu, ZHANG Yiqing, ZHAO Jun, et al. Study on near infrared reflectance sensor for high sediment concentration measurement[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(7):51.

[14] 高贵成，褚杰辉，高国甫，等. 非接触式超声波水位计钢塔设计[J]. 气象水文海洋仪器, 2001(4):23. CAO Guicheng, ZHU Jiehui, GAO Guopu. The design of steel tower installed to the no-contact ultrasonic water gauge[J]. Meteorological,Hydrological and Marine Instruments, 2001(4):23.

[15] 胡吉华，徐国龙，曹国华，等. 基于陶瓷电容传感器的压力水位计的研制[J]. 水利信息化, 2013(2):33. HU Jihua, XU Guolong, CAO Guohua, et al. Pressure water level meter based on ceramic capacitive pressure sensor[J]. Water Resources Informatization. 2013(2):33.

[16] 许笠，王延乐，华小军. 雷达水位计在水情监测系统中的应用研究[J]. 人民长江, 2014,45(2):74. XU Li, WANG Yanle, HUA Xiaojun. Research on application of radar level meter in automatic water regime monitoring system[J]. Yangtze River, 2014,45(2):74.

[17] 孟虹宇. 水位计标定系统的研究与设计[D]. 东北大学, 2013:21. MENG Hongyu. The research and design of the benchmark system for water level instrument[D]. Northeastern university, 2013:21.

Test and calibration of a real-time hillslope runoff measuring device

Li Zhiguang1， Cao Wenhua1， Niu Yong2

(1.Monitoring Center of Soil and Water Conservation, Ministry of Water Resources, 100053, Beijing, China;2.Shandong Agricultural University, 271018, Tai′an, Shandong, China)

[Background] Water and soil loss has been a major environmental issue, and people’s demands on environment quality are raised constantly in China. In this context, a nationwide water and soil loss monitoring network was set up, the count of water and soil loss monitoring stations increased to 738 recently. Although network built quickly, but the dedicated devices used in water and soil loss monitoring still fall behind very much. For example, manual throughfall collecting tank was invented centuries ago, but it’s still used widely now in China. Therefore, developing and testing automated dedicated devices used in water and soil loss monitoring is an urgent and long-term task, which can enhance people’s ability of monitoring and controlling water and soil loss. Automatic hillslope runoff measuring device is a gauge that can be used in a scale of runoff plot to replace human beings to measure, which can enhance the monitoring efficiency greatly. [Methods] This paper took the measurement accuracy of a Runoff & Sediment Real-time Measuring Device as research object, the relative errors between theoretical value and measurement value were calculated based on the artificial runoff-producing simulation. Analysis of partial correlation was used to uncover the cause of error. With regression analysis, a fitted relationship between the runoff true value and the measured value was established. [Results] The results showed that the range of the relative error of runoff was -4.33%-24.01%，and the range of the stabilization time was 55-130 s. Based on the analysis of partial correlation, the stabilization time for measured values had a significantly positive correlation with sediment concentration, and had a significant inverse correlation with design flow (P<0.05). The accuracy of measurement had a significantly positive correlation with sediment concentration and design flow, but both sediment concentration and design flow presented limited influences on accuracy of measurement(α= 0.05). Regress equation between the measurement of runoff and revised values was found by using the regression analysis. It was proved that accuracy of the measurement and the stabilization time for runoff measurements was significantly improved. Furthermore, the research also demonstrates that increasing waves cutting device and enlarging the size of waves filter can be conducive to improve accuracy of the measurement. [Conclusions] These results were beneficial to understand the measuring performance of device in this study. With the rainfall intensity range 3.60 mm/h-66.96 mm/h, runoff can be measured accurately by the device, the range of rainfall intensity mentioned above can represent different rain types, such as moderate rain, heavy rain and rainstorm in northern China. For improving measurement accuracy in the future，the impact of silt content and mechanical composition should be considered and explored.

observation based on runoff plot; flow; measurement accuracy; modified model; partial correlative analyses

2017-03-06

2017-05-16

项目名称： 山东省自然基金中青年科学家科研奖励基金项目“半干旱半湿润地区城市绿地节水与降温效应机制研究”(ZR2016DB12)；全国水土流失动态监测与公告项目(1261521610273)；高分水利遥感应用示范系统(一期)(08-Y30B07-9001-1315)

李智广(1966—)，男，教授级高级工程师。主要研究方向：水土保持监测。E-mail：lizhiguang@mwr.gov.cn

S274.1

A

2096-2673(2017)03-0058-07

10.16843/j.sswc.2017.03.008