复杂曲面等残留高度螺旋刀具轨迹生成方法的研究*

蔡有杰，姜淑凤，王世刚，陶贞钧

(齐齐哈尔大学 机电工程学院，黑龙江 齐齐哈尔 161006)



复杂曲面等残留高度螺旋刀具轨迹生成方法的研究*

蔡有杰，姜淑凤，王世刚，陶贞钧

(齐齐哈尔大学 机电工程学院，黑龙江 齐齐哈尔 161006)

复杂曲面加工中，刀具轨迹规划是数控加工技术的关键，它的优劣性将直接影响曲面加工的精度和效率。在总结等残留高度法和螺旋走刀模式的特点基础上，对等残留高度法进行改进，提出了基于等残留高度法的螺旋加工模式刀具轨迹生成方法，给出了该方法的生成刀具轨迹的流程。该方法解决了等残留高度法轨迹线零散、轨迹不光滑、不利于高速加工的缺点，实现了加工轨迹光滑连续，在确保加工精度的前提下，提高了曲面加工效率。最后，利用此方法对叶片零件加工实例进行了刀具轨迹规划，在UG加工模块中完成了加工仿真，验证了方法的优越性。

复杂曲面；等残留高度法；螺旋刀轨；五轴数控机床

0 引言

当前，具有复杂曲面造型的产品越来越多，并且广泛应用在汽车、模具、航空航天、航海等领域当中，例如潜艇的螺旋桨叶片的造型设计、汽车和高速列车的外形设计、涡轮增压发动机中涡轮叶片的设计等。复杂曲面是以复杂并且自由变化的形式存在的，其结构相对复杂、精度要求高、难以用简单的数学解析公式所表达。因此，复杂曲面的加工较为困难，该问题也成为了国内外学者竞相研究的焦点。

许多学者在常用的刀具轨迹生成方法的基础上进行局部优化和改进。Li和Feng提出了一种球头铣刀三轴数控机床曲面加工的刀具轨迹生成方法，这种方法对对等残留高法进行了改进，有效的缩短了加工的总长度[1]。Ding在等平面法的基础上进行了改进，通过在不同加工区域上引入等照度线，进而自适应生成加工刀具轨迹的方法[2]。印度学者Agrawal和Bezbaruah等利用遗传算法的有点对等残留高度法进行了改进，提出了一种针对于复杂曲面数控加工的等残余高度刀具轨迹生成算法[3-4]，这种方法有效的提高了加工效率。沈阳理工大学的梁媛、李丽等人针对于五轴数控曲面加工提出了一种基于STEP-NC的NURBS曲面五轴加工的刀具轨迹生成方法[5-6]，该方法提高了复杂曲面五轴数控加工的精度和效率。清华大学的樊文刚等人建立了多点切触刀位优化的通用数学模型[7]，并使其在实际加工中发挥了优势。还有一些学者在传统的刀具轨迹生成方法的基础上做了优化，提高了加工效率[8-10]。

等残留高度法是曲面加工刀轨生成的重要方法之一，利用该方法生成的加工路径，加工后相邻两条刀轨的残留高度是恒定的，被加工曲面的表面粗糙度较为均匀，加工精度高；本文在等残留高度法的基础上进行改进，将螺旋走刀模式和等残留高度法有效的结合在一起，取两者的优点进行融合，使得刀具轨迹线平滑，适用于复杂曲面加工中，提高曲面加工的精度和效率。

1 等残留高度法的基本思想

等残留高度法的基本思想是：首先选取曲面上的一条边界曲线对其进行离散生成初始刀具轨迹，根据待加工曲面最大残留高度的要求，按照递归算法将初始轨迹进行推进，生成新的刀具轨迹，直到覆盖满整个待加工曲面。首先建立一个链表，链表中存储的是当前刀触点还未经过的下一条螺旋刀轨上的一些关键点。这些点是根据当前刀触点所在刀轨上刀触点并考虑等残留高度要求计算出来的下一个螺旋刀轨上对应的点。当刀具走到当前刀触点的时候，根据链表元素中点的信息计算下一个刀触点，然后再根据当前刀触点，计算下一个螺旋刀轨中相应的点，并将该点信息添加到链表的末尾。依次循环下去，便会产生螺旋的刀轨，一直到生成整张曲面的刀轨。

1.1 切削步长的确定

设被加工曲面上一点位置矢量s(ui,vi)=(x(ui,vj),y(ui,vj),z(ui,vj),t(ui,vj))，即si,j=(xij,yij,zij,tij)。

若当刀触点位置矢量为s0,0=(x0,0,y0,0,z0,0,t0,0)，链表中第一个元素位置矢量为s1,1=(x1,1,y1,1,z1,1,t1,1)，链表中第一个元素位置矢量为：

T=s1,1-s0,0=(x1,1-x0,0,y1,1-y0,0,z1,1-z0,0,t1,1-t0,0)

(1)

如果需要更高的精度，可以取出链表中更多的点，利用样条曲线对这些点进行插值，然后以点处的切线方向作为切削方向。

设该点两个主曲率为k1k2，沿切削方向法曲率为km，若根据三角公式见算出T与k1，所在方向的夹角φ，则根据欧拉公式有：

km=k1cos2φ+k2sin2φ

(2)

1.2 相邻刀轨点的计算

沿着垂直当前切削方向计算下一个螺旋刀轨上的对应点。该点与当前刀触点之间的距离被称作行距，一般来说，行距是残留高度、刀具半径以及该方向法曲率半径的函数，在残留高度和刀具半径一定的情况下，行距由曲面的局部形状来决定。

设垂直切削方向法曲率为，根据欧拉公式，推导得出：

Kn=k1+k2-km

(3)

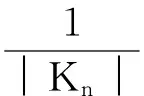
(4)

式中：对于凹曲面，取负号；对于凸曲面，取正号。

以上是五轴数控机床复杂曲面加工等残留高度螺旋刀具轨迹生成的方法，利用此方法解决了等残留高度法轨迹线零散、轨迹不光滑、不利于高速铣削的缺点，实现了加工轨迹光滑连续，在确保加工精度的条件下，提高了加工效率。

2 等残留高度螺旋刀具轨迹生成

环形初始轨迹和螺旋初始轨迹的区别在于前者轨迹的起点与终点重合，而后者的初始轨迹的终点是是下一条轨迹的起点。由于自由曲面的造型各不相同，曲率变化也不同，在选取边界曲线作为初始轨迹的时候，首尾两条相邻边界曲线的连接方式也各不相同。

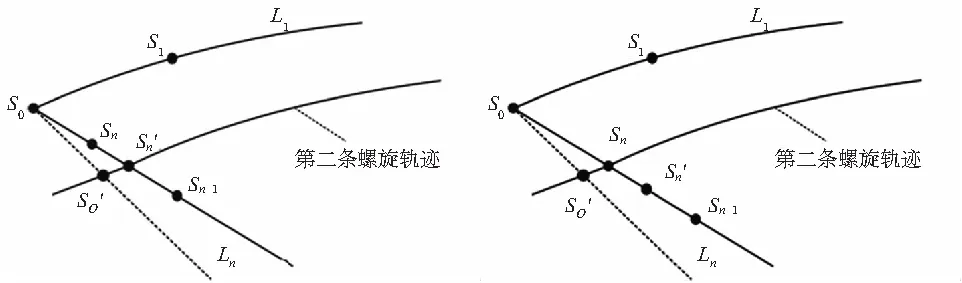
图1 起始和末尾边界曲线之间的夹角小于或等于90°情况

图2 起始和末尾边界曲线之间的夹角大于90°情况

(3)若选取的边界曲线是圆形边界曲线，那么这种情况第一条边界曲线和末端边界曲线在连接点处二阶连续，两条曲线为同一条曲线。这种情况在首尾曲线连接处前后加工方向是不会发生改变的，由于这一限制，无法生成覆盖满整个待加工曲面的螺旋轨迹，本文利用添加辅助过渡曲线的方法解决此问题，如图3所示，有效的生成螺旋轨迹线。

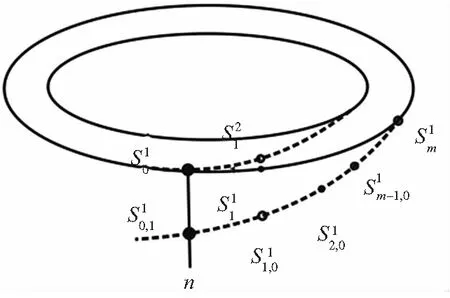
图3 起始和末尾边界曲线在同一条直线上情况

具体生成方法如下步骤：

STEP 1：首先要根据待加工曲面确定过度路径的长度L，当刀具沿着过度路径切削被加工表面时，刀具与待加工表面的接触面积会逐渐增大，同时切削力也会越来越大，过度边L与切削力是成反比的关系。因此过度边L越大，切削力的变化率就越小，越有利于保护刀具寿命和提高表面加工精度。反之，若过渡边过长将会影响加工效率。

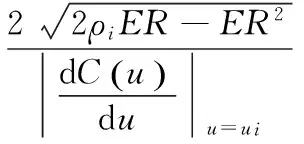
(5)

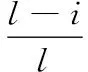
(6)

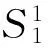
利用以上方法求得初始轨迹，并利用等残留高度法对轨迹线进行偏置，直到整个待加工曲面被轨迹线覆盖满为止；传统的等残留高度法是通过利用最大残留高度的算法偏置初始轨迹，没有考虑加工行距的因素，因此偏置后得到的加工轨迹可能不能完全覆盖整个待加工表面。本文以传统的螺旋刀具轨迹法为基础，对其进行了部分优化：

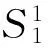
(7)

通过上述方法得到的加工轨迹中相邻的两条轨迹线之间的加工行距是最大残留高度的一半，所以可以避免螺旋轨迹不能覆盖整个曲面的问题。

3 叶片零件实例验证

通过加工实例来验证本文提出的刀具轨迹规划方法是否适用于曲面加工中，在UG软件数控加工模块中分别利用本文提出的等残留高度螺旋轨迹法和传统的方法对叶片零件，如图4所示，进行刀具轨迹规划并完成加工仿真，通过对比两者的加工轨迹线和加工精度，验证本文所述方法在曲面加工中的优越性。

叶片属于复杂曲面零件，型面扭曲度较大是叶片零件的主要特点，因此对其进行加工难度较大。由于叶片零件属于曲面零件，加工难度较大，因此加工设备选用五轴数控机床对其进行加工；加工坐标原点设置为叶片与底座连接方块中心上；刀具选择D8R4的球头铣刀。加工本工件的毛坯为圆棒料，材料牌号为合金，采用三爪卡盘将其底面固定安装在机床B轴。

图5为基于等残留高度法的螺旋走刀模式轨迹，图6为传统方法的加工轨迹。从两者的轨迹图中可以看出，图5加工路径光滑，连续性好，避免了多次的抬刀的现象；从图6中可以看出在加工轨迹转角处出现大量自相交轨迹，这种情况严重影响加工效率和质量。图7为等残留高度螺旋轨迹法对叶片零件进行加工刀具轨迹规划，利用五轴数控机床对其进行加工后得到的结果。

实例中分别采用等残留高度法螺旋走刀模式和传统方法对叶片零件进行加工，对比两者的轨迹得知，等残留高度螺旋轨迹法比传统方法更适合在曲面加工中进行轨迹规划，利用前者规划出的轨迹线光滑、无需多次抬刀、并且轨迹线无自相交现象，避免了传统方法中螺旋轨迹线无法覆盖整个待加工曲面的问题，提高了曲面加工的精度和效率。

图4 叶片模型 图5 等残留高度螺旋轨迹

图6 传统螺旋轨迹 图7 叶片加工成型示意图

4 结论

刀具轨迹规划是复杂曲面加工中的难点，是影响曲面加工精度和效率的重要因素。本文在原等残留高度法的基础上有效的结合了螺旋轨迹的优点，提出了一种基于等残留高度法的螺旋走刀模式，这种方法避免了初始环形轨迹对角线连接所带来的精度差的问题，在传统方法的基础上提出一种螺旋刀具轨迹直接生成法，在根据等残留高法对轨迹线进行偏置，在残余高度设计环节本章选定的参数为最大残留高度的一半，这样避免了传统方法中螺旋轨迹线无法覆盖整个待加工曲面的问题。

[1] Feng H Y, Li H W. Constant scallop-height tool path generation for three-axis scuiptured surface[J]. Computer-Aided Design, 2002, 34: 647-654.

[2] Ding S. Adaptive iso-planar tool path generation for machining of free-form surfaces[J]. Computer-Aided Design, 2003, 35: 141-153.

[3] Rajneesh Kumar Agrawal, D K Pratihar. Optimization of CNC iso scallop free form surface machining using a genetic algorithm[J]. International Journal of Machine Tool & Manufacture, 2005, 62(11): 1-9.

[4] V Giri, D Bezbaruah, P Bubna. Selection of master cutter paths in sculptured surface machining by employing curvature principle[J]. International Journal of Machine Tool & Manufacture, 2005, 45(11): 1202-1209.

[5] 梁媛，孙建业，王国勋．NURBS曲面五轴加工刀具规迹生成技术研究[J]．工具技术，2014,48(7)：37-42．

[6] 李丽，房立金，王国勋．NURBS曲面五轴加工刀具路径规划技术研究[J]．机械制造，2014(2)：5-9．

[7] 樊文刚，叶佩青．复杂曲面五轴端铣加工刀具轨迹规划研究进展[J]．机械工程学报，2015，51(15)：168-182．

[8] 周波，赵吉宾，刘伟军，等．基于参数曲面映射的五轴数控螺旋加工轨迹计算方法[J]．机械工程学报，2013，49(5)：100-109．

[9] 韦尧兵，廖波，李运．基于等残留高度的自由曲面加工刀具轨迹规划[J]．新技术新工艺，2013(12)：63-65．

[10] 李万军，牛敏．多岛屿曲面的刀具轨迹规划算法研究[J]．组合机床与自动化加工技术，2015(5)：123-126．

(编辑 李秀敏)

Research on Spiral Tool Path Generation Method of Constant Scallop Height for Complex Curved Surface

CAI You-jie, JIANG Shu-feng, WANG Shi-gang,TAO Zhen-jun

(School of Mechatronics Engineering, Qiqihar University, Qiqihar Heilongjiang 161006, China)

Tool path planning is the key of NC machining technology, and its advantages and disadvantages will directly affect the accuracy and efficiency of surface machining. At the conclusion of the scallop height method and spiral tool modes on the basis of equivalence, residual height method was improved, and puts forward the method of spiral machining mode of tool path generation based on constant scallop height method, the tool path generation method of the process is given. This method solves the scallop height method path, scattered path is not smooth, not conducive to the realization of high speed machining defects, machining path smooth and continuous, in the premise of ensuring the machining accuracy, improve machining efficiency. Finally, this method is used to process the tool path planning of the blade parts machining. The machining simulation is completed in the UG processing module, and the superiority of the method is verified.

complex curved surface;the constant scallop height method;spiral tool path；five axis cnc machine tool

1001-2265(2017)06-0059-03

10.13462/j.cnki.mmtamt.2017.06.015

2016-11-28；

2016-12-30

“高档数控机床与基础制造装备”科技重大专项课题(2011ZX04001-011-4)；齐齐哈尔市科技局科学技术计划项目工业攻关(GYGG-201418，GYGG-201505)

蔡有杰(1966—)，男，吉林通榆人，齐齐哈尔大学副教授，研究方向为机械电子工程，(E-mail)86464642@qq.com。

TH162;TG506

A