多路功率分流齿轮啮入时序的优化研究

林定笑， 陈栩， 刘伟强， 苏坚毅， 施智鹏

(福建工程学院 机械与汽车工程学院， 福建 福州 350118)

多路功率分流齿轮啮入时序的优化研究

林定笑， 陈栩， 刘伟强， 苏坚毅， 施智鹏

(福建工程学院 机械与汽车工程学院， 福建 福州 350118)

针对传统外啮合齿轮箱功率密度较小，传递大功率时增大模数而导致齿轮箱尺寸剧增的问题，基于渐开线标准齿轮传动正确啮合条件及重合度计算理论，提出以多路功率分流外啮合定轴齿轮传动替代传统单外啮合齿轮传动，根据啮入点啮入时序排布方式，设计了同步啮入与依序逐步啮入两套方案。以3路功率分流的外啮合定轴齿轮传动为案例，通过复合重合度计算推导，发现在相同重合度下，与同步啮入时序方案相比，采用依序逐步啮入时序方案，齿轮传动更为平稳，在相同传动比、相同模数情况下，齿轮承载能力提高1/3。由此得出结论，以多路功率分流外啮合定轴齿轮传动，并采用各路啮入点依序逐步啮入时序方案，可以在有效提高齿轮箱的功率密度，大幅减少齿轮箱尺寸基础上，获得平稳传动，提高齿轮承载能力。

多路功率分流； 复合重合度； 啮入点； 啮入时序

机械传动以齿轮传动为主，高功率密度、节能环保的齿轮传动系统是齿轮研究的主要方向。传统的直齿圆柱齿轮外啮合时，齿轮连续传动的条件是重合度大于1小于2，即同时参与啮合的轮齿对数处于1和2间[1]206。传统齿轮传动提高传递功率的一般方法是通过增大模数或提高重合度，然而模数增大导致齿轮箱尺寸激增，无法有效提高齿轮箱功率密度；冯辉英等[2]分析了重合度对齿轮传动的影响，渠珍珍等[3]提出了高重合度齿轮的实现方法，但该方法对单对外啮合齿轮箱的功率密度提高效果并不明显。本文基于渐开线标准齿轮传动正确啮合条件及重合度计算理论，采用多路功率分流的定轴齿轮替代传统的外啮合直齿圆柱齿轮传动，以3路功率分流的外啮合定轴齿轮传动齿轮箱设计为案例，进行理论推导和案例分析，研究功率分流齿轮传动在相同重合度下的各路啮入点啮入时序优化方案。

1 单对外啮合齿轮副的重合度计算[1]207

齿轮机构的传动由两齿轮轮齿依次啮合实现，如图1所示为一对外啮合齿轮传动示意图。

图1中齿轮1为主动轮，齿轮2为从动轮，图中N1N2为理论啮合线，B1B2为实际啮合线。传动时齿轮1带动齿轮2转动，两齿轮中的一对轮齿进入啮合，啮合起始点(啮入点)为齿轮2的轮齿齿顶与N1N2的交点B2，啮合点沿着N1N2渐进移动，齿轮1轮齿上的啮合点向齿顶方向移动，而齿轮2轮齿上的啮合点向齿根方向移动。当齿轮1轮齿上的啮合点到达齿顶(齿轮1的齿顶圆与啮合线N1N2的交点B1)时，两轮齿啮合结束，故B1为轮齿的啮合终止点(啮出点)。若要使齿轮连续传动，就必须在前一对轮齿尚未退出啮合，后一对轮齿及时进入啮合。故齿轮连续传动的条件是实际啮合线B1B2≥Pb[1]206(Pb为基圆上的齿距)。

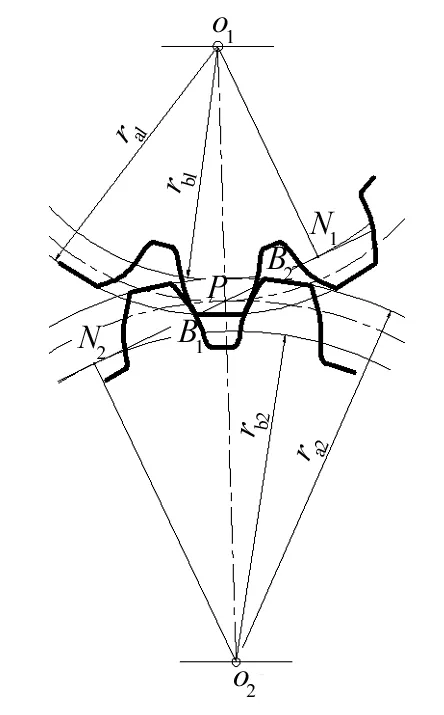
图1 一对外啮合齿轮传动示意图Fig.1 Sketch of the transmission of a pair of external meshing gears

实际啮合线的长度B1B2与Pb之比为齿轮传动的重合度，表示为εα[1-8]。

(1)

式(1)中,αa1、αa2分别为齿轮1、2的齿顶圆压力角；z1、z2分别为齿轮1、2的齿数；α′为啮合角(节圆压力角)。

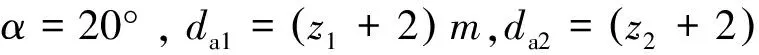
(2)

将α′=α及式(2)代入式(1)可得：

(3)

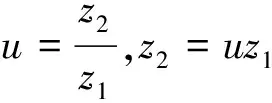
(4)

由公式(4)得出重合度εα与主动轮齿数z1和传动比u之间的关系曲线如图2所示。从图2可以看出，当z1≥17，且1.5≤u≤5时，εα>1.55。z1越大、u越大时，εα越大。重合度是衡量齿轮连续传动的条件，代表同时参与啮合的轮齿对数的平均值[1]。如图3所示，B1D与B2C为双对齿啮合区，DC为单对齿啮合区。单对外啮合齿轮副啮合齿数对随时间变化情况如图4所示，可以看出，单对外啮合齿轮副啮合齿数对随时间在2对与1对间周期性变换，重合度越大，啮合齿数对为2对时所占时间比越大，齿轮传动平稳性越好，越有利于提高承载能力。

图2 不同z1、u时的εα 曲线图Fig.2 εα curve under different z1 and u

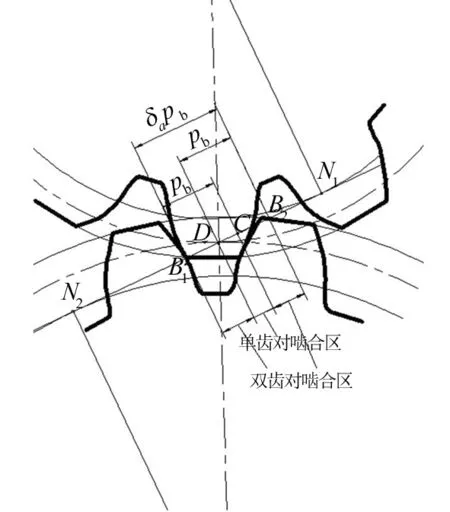
图3 单、双对齿啮合区示意图Fig.3 Meshing area of single tooth and pair teeth

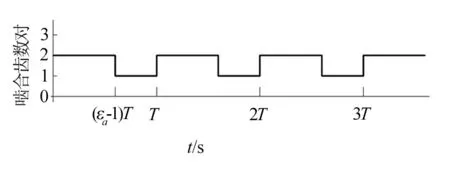
图4 单对外啮合齿轮副啮合齿数对变化图Fig.4 The meshed teeth pair change graph of single-pair externally meshed gear

2 在相同复合重合度下的多路功率分流定轴齿轮传动啮入点啮入时序方案

多路功率分流的定轴齿轮传动中，主动轮安装于中心轴，多路从动轮均匀布置于以主动轮为中心的圆周上，由外啮合产生的径向力彼此平衡抵消，使径向支承力接近于零，各从动轮分担输入扭矩。由于功率分流，同时承受载荷的轮齿数量多，从而使之能在更小的模数下具有更高的传动比，传动更平稳。

不同于单对外啮合齿轮传动，多路功率分流的外啮合定轴齿轮传动，主动轮轮齿上的啮合线有多处，功率分流定轴齿轮传动的总重合度应为多对外啮合齿轮副的复合重合度。如图5，设多路功率分流外啮合定轴齿轮传动为3路功率分流， 且令z1=17，u=2，则复合重合度εα0=3εα，从图2可以得出εα=1.6，此时εα0=4.8。

在复合重合度相同的情况下，多对外啮合齿轮副对应的各路啮入点可以有不同的啮入时序。各路啮入点啮入时序不同，啮合齿数对的变化有很大不同，极大地影响齿轮传动的平稳性和齿轮箱的功率密度。根据上述案例给定的参数，设计了以典型外啮合齿轮的同步啮入和依序逐步啮入两套时序传动方案，进行分析比较，寻求一种较优的多路功率分流定轴齿轮传动时序方案。

(1)各路啮入点同步啮入方案

如图5，齿轮按中心轴对称的均布外啮合布置，每一对外啮合齿轮副看作单外啮合齿轮副，啮合齿数对随时间变化如图4。每一对外啮合齿轮副开始啮合点(啮入点)均为从动轮的齿顶圆与啮合线的交点，随着啮合传动，轮齿啮合点沿啮合线移动，主动轮轮齿上的啮合点逐渐向齿顶移动。

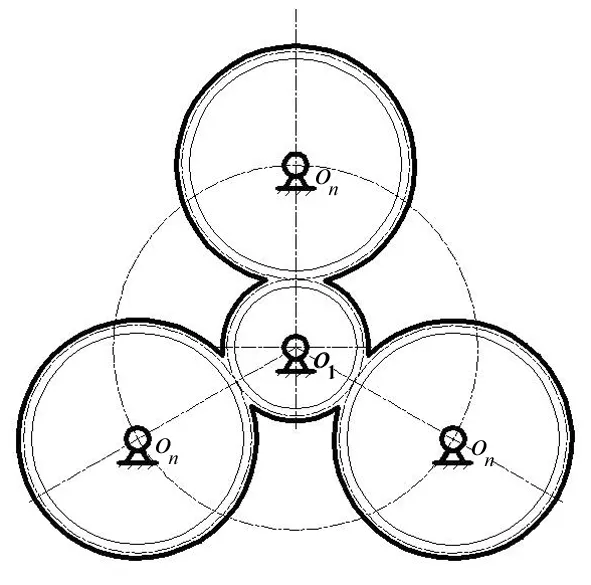
图5 多路功率分流定轴齿轮传动示意图Fig.5 Transmission of multi-channel power split fixed-axis gear

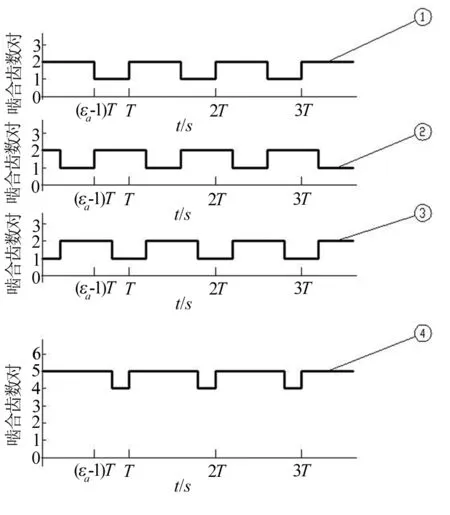
图6 各路啮入点同步啮入时啮合齿数对变化图Fig.6 The change of meshed teeth pair when multi-channel meshing points synchronously mesh in

如图6，图中曲线①、② 、③分别为3对外啮合齿轮副啮合时啮合齿数对随时间变化状态，可以看出，3个主动轮轮齿上的啮入点啮入时间和啮出点啮出时间均相同，即各路啮合是同步啮入和啮出的，此时总啮合齿数对随时间变化状态如图6中曲线④所示。从曲线④可以看出，总啮合齿数对随时间在6对与3对间周期性变换。

(2)各路啮入点依序逐步啮入方案

将3对主动轮轮齿上的啮入点啮入时序进行适当排布。如图7，图中曲线①、②、③分别为3对齿轮副啮合齿数对随时间变化状态，从图中可以看出，3对主动轮轮齿上的啮入点啮入时间不同，当第一对齿轮副(假定为曲线①)进入单对齿啮合时，第二对齿轮副(假定为曲线②)进入双对齿啮合；而当第二对齿轮副(假定为曲线②)进入单对齿啮合时，第三对齿轮副(假定为曲线③)进入双对齿啮合，即各路啮合是依序逐步啮入和啮出的，此时总啮合齿数对随时间变化状态如图7中曲线④所示。可以看出，三路齿轮总啮合齿数对随时间在5对与4对间周期性地变换。

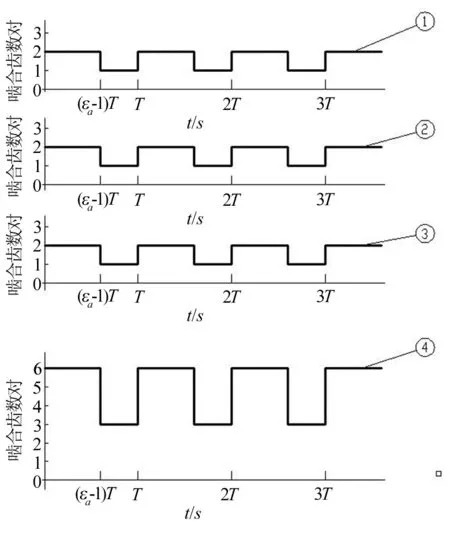
图7 各路啮入点依序逐步啮入时啮合齿数对变化图Fig.7 The change of meshed teeth pair when multi-channel meshing points gradually mesh in

3 两套方案的优劣比较分析

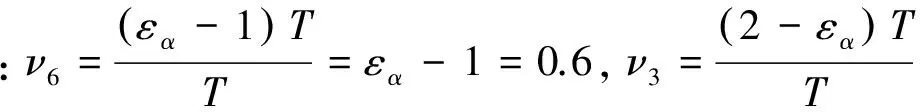
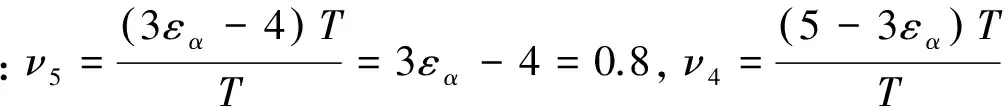
从以上两套时序方案的推导计算结果来看，在复合重合度相同的情况下，各路啮入点同步啮入时参与啮合的齿数对最少时仅为3对，最多时达到6对，啮合齿数对6对的时间比为0.6，啮合齿数对为3对的时间比为0.4。由于啮合齿数对在3对与6对间周期性切换，主动轮参与承载的轮齿数在3个和6个间变化，在传递功率不变的情况下，主动轮上承载轮齿在切换时扭矩变化剧烈，导致齿轮传动振动幅度大大增加，严重影响传动的平稳性。而且按齿轮承载能力选取模数时，因其参与啮合的齿数对最少时仅为3对，在相同功率和相同齿数(传动比相同)的情况下，模数可选为单对齿轮传动时的1/3。

而各路啮入点依序逐步啮入时参与啮合的齿数对最少可达4对，最多仅5对，其中啮合齿数对为5对的时间比为0.8，啮合齿数对为4对的时间比为0.2。由于是在4对与5对间周期性切换，主动轮上参与承载的轮齿在4个和5个间变化，在传递功率不变的情况下，主动轮上的承载轮齿在切换时扭矩变化不大，切换冲击较小，使得齿轮振动幅度小，大大提高传动的平稳性。按齿轮承载能力选取模数时，因其参与啮合的齿数对最少为4对，在相同功率和相同齿数(传动比相同)的情况下，模数仅为单对齿轮传动时的1/4，可以大幅减少齿轮箱尺寸，更为有效地提高齿轮箱的功率密度。

4 结论

采用多路功率分流的定轴齿轮替代传统的外啮合直齿圆柱齿轮传动，优先选用各路啮入点依序逐步啮入时序方案，齿轮传动平稳。在相同传动比、相同模数情况下其承载能力是单对外啮合齿轮传动的4倍，采用各路啮入点依序逐步啮入，齿轮承载能力比各路啮入点同步啮入方案提高了1/3。

[1] 孙桓，陈作模，葛文杰.机械原理[M].北京：高等教育出版社，2013.

[2] 冯辉英，于兴芝.基于重合度对齿轮传动影响分析[J].现代机械，2009(9)：7-9.

[3] 渠珍珍，杨杭旭.高重合度齿轮的实现方法及其参数设计[J].机电技术，2012，6(3)：103-105.

[4] 贺建群，张峥嵘.渐开线圆柱齿轮传动的重合度计算[J].机械设计与制造，2005，9(9)：25-26.

[5] 唐立山.一种新的渐开线直齿圆柱齿轮传动理论重合度算法[J].机械设计与制造，2012，2(2)：54-55.

[6] 李建功.对GB3480-83中直齿轮重合度系数Zε的商榷[J].河北理工学院学报，1999，21(1):25-28.

[7] 田培棠，田凌.圆柱齿轮几何计算原理及实用算法[M].北京：国防工业出版社，2012.

[8] 邵忍平. 机械系统动力学[M].北京：机械工业出版社，2005.

(责任编辑： 陈雯)

Optimization of the meshing time sequence of multi-channel power split gear

Lin Dingxiao, Cheng Xu，Liu Weiqiang, Su Jianyi, Shi Zhipeng

(College of Mechanical and Automotive Engineering, Fujian University of Technology, Fuzhou 350118, China)

To improve the power density of externally meshing gear box and to reduce the dimension of the gear box at large power transmission, multi-channel power split externally meshing fixed-axis gear transmission was presented based on standard gear transmission meshing condition and contact degree calculation theory to replace the traditional single externally meshing gear transmission. Synchronously meshing-in time sequence scheme and gradually ordered meshing-in time sequence scheme were designed in accordance with the meshing time sequence arrangement mode. In the case of three-channel power split externally meshing fixed-axis gear transmission, the gear transmission of the gradually ordered meshing scheme is more smooth compared to that of the synchronously meshing scheme, with the bearing capacity of the gear increasing by 1/3 under the same contact degree, the same transmission ratio and the same modulus. The results indicate that multi-channel power split externally meshing fixed-axis gear transmission integrated with the gradually ordered meshing scheme can implement smooth transmission and improve the gear bearing capacity while effectively increasing the power density of the gear box and reducing the dimension of the gear box.

multi-channel power split; compound contact ratio; meshing point; meshing time sequence

10.3969/j.issn.1672-4348.2017.03.006

2016-12-16；

2017-03-15

林定笑(1969- )，男，福建福清人，副教授，硕士，研究方向：机械工程。

TH132.417

A

1672-4348(2017)03-0229-05