一种基于等效线性化的非平稳随机动力响应分析的显式迭代算法*

李雪平 王坤 魏鹏 苏成

(华南理工大学土木与交通学院,亚热带建筑科学国家重点实验室,广州 510000)

一种基于等效线性化的非平稳随机动力响应分析的显式迭代算法*

李雪平 王坤 魏鹏 苏成†

(华南理工大学土木与交通学院,亚热带建筑科学国家重点实验室,广州 510000)

提出了一种基于等效线性化法的非平稳随机动力响应分析的显式迭代算法.首先根据等效线性化法把非线性系统转化为离散的线性系统,然后应用Newmark-β积分方法,推导出各个离散时刻的时域显式迭代公式,进而可以快速得到非线性系统的随机动力响应,最后用一个非线性的范德波尔系统和一个杜芬系统受非平稳随机荷载的算例验证了该算法的计算精度和计算效率.

非线性系统, 非平稳, 随机, 等效线性化, 显式迭代算法

引言

土木工程结构不可避免地会受到一些随机荷载的作用,如地震、风和波浪等.为了防止工程结构不受破坏,设计时必须分析结构在随机荷载作用下的随机动力响应.在工程实践领域,线性系统的随机振动理论已经发展得较为成熟[1-4].实际结构往往呈现一定的非线性特性,但实际情况只有少数的非线性系统可以得到精确解[5-8],其他情况都广泛采用数值积分的方法.上述大部分情况,非平稳随机荷载被简化为平稳随机荷载.

事实上,很多随机荷载呈现非常明显的非平稳特征.一直以来,等效线性化法广泛应用于非线性系统在随机荷载下的随机响应分析[9-15],但是由于计算量大的原因,只研究了自由度比较少的情况[16].对于多自由度非线性系统在非平稳随机激励下的响应分析一般还是采用蒙塔卡罗模拟,但是对于工程中大型结构而言,其计算效率远远不够.最近,苏成等[17-20]提出了快速计算线性系统在非平稳随机荷载下的动力分析的时域显式法.本文在此基础上,将非线性系统采用等效线性化法转化为线性系统,借助Newmark-β积分公式,提出了一类基于等效线性化法的非线性系统在非平稳随机地震动力响应分析的显式迭代算法.

1 非线性系统等效线性化

一个n自由度非线性系统在受地震荷载作用下的动力学方程如下：

(1)

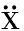
(2)

根据等效线性化方法[11-12],离散的非线性系统(2)可以用以下的线性系统近似替代：

(3)

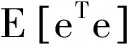
(4)

(i,j=1,2…n)

(5)

经推导,式(5)可变为：

(6)

要计算式(6),需要先计算系统(2)的统计响应,首次计算时非线性恢复力为零.这样式(3)～(6)构成一个迭代循环,最终达到收敛时就得到了mΔt时刻的随机响应,下一时刻依次推进,就可以到得到非线性系统在非平稳荷载下的所有时刻的统计响应.

2 基于Newmark-β积分的显式迭代算法

最常用的求解动力方程的方法是直接积分法,直接积分一般分为显式积分和隐式积分两种格式,显式积分格式是无条件稳定的,而隐式积分格式的稳定性依赖于时间步长.所以本文选用Newmark-β显式积分格式[21],其主要的公式如下：

(7)

(8)

式中β和γ为积分参数.将方程(7)和方程(8)变形可以得到速度和加速度的表达式如下：

(9)

(10)

式(9)和(10)中的参数为：

(11)

将式(9)和(10)代入方程(3),可以得到位移的表示式如下：

(12)

式(12)参数为：

D1=D4[b1(M+Mm)+a1(C+Cm)]

(13)

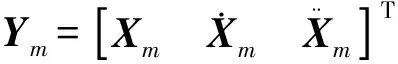
(14)

式(14)中系数为：

(15)

式(15)中I为单位矩阵.

当初始值Y0和非线性恢复力Qm为零时,矩阵E和F为常矩阵.此时式(14)可以展开为如下形式：

(16)

引入变量

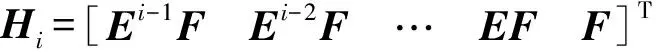
式(16)可以化简为：

Yi=HiPi

(17)

(18)

σYi=cov(Yi,Yi)=Hicov(Pi,Pi)HiT

(19)

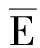
当初始值Y0为零,非线性恢复力Qm不为零时,式(14)中的E和F为时变矩阵.此时,非线性系统的随机响应可以通过时域显式迭代方法求解,具体流程如下：

当m=1时,Δt时刻的初始协方差为：

=H1cov(P1,P1)H1T

(20)

式(20)中H1=F01.矩阵F01可以通过式(15)计算,初始时令非线性恢复力为零.假定经过i次迭代满足收敛准则,那么Δt时刻的解为：

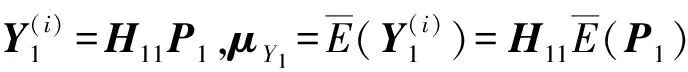
(21)

当m=2时,2Δt时刻的初始随机响应为：

=H2cov(P2,P2)H2T

(22)

(23)

当m=n,n为3,5,7…等奇数时,nΔt时刻的初始随机响应为：

=H1cov(Pn,Pn)H1T

(24)

(25)

当m=n+1,m为4,6,8…等偶数时,(n+1)Δt时刻的初始随机响应为：

(26)

(27)

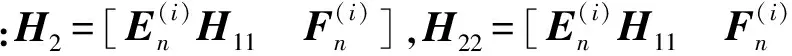
H11是上一时刻经过迭代收敛后的矩阵,这样经过少数几次迭代结果就能收敛.同时随机荷载的协方差矩阵cov(Pn,Pn)可以提前计算并储存.此外,推导过程中采用的Newmark-β积分公式无条件稳定,积分步长Δt可以取的相对大一些.

3 数值算例

3.1 算例1：六自由度范德波尔系统

考虑一个6自由度的范德波尔系统受非平稳随机荷载的作用,其运动方程如下：

(i=1,…,6)

(28)

(29)

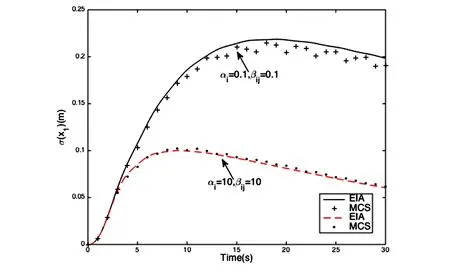
图1 位移X1的标准差Fig.1 Standard deviation of displacement X1

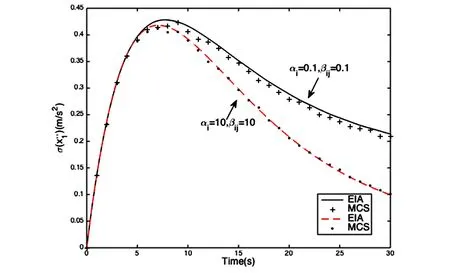
图2 加速度1的标准差Fig.2 Standard deviation of 1

表1 蒙塔卡罗模拟与显式迭代算法的效率对比

3.2 算例2：四十自由度杜芬系统

考虑如图3所示的一个40自由度的杜芬系统受非平稳随机地震荷载的作用,其运动方程如下：

(30)

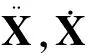
(31)

式(31)中η1=…=η20=500,η21=…=η40=600.

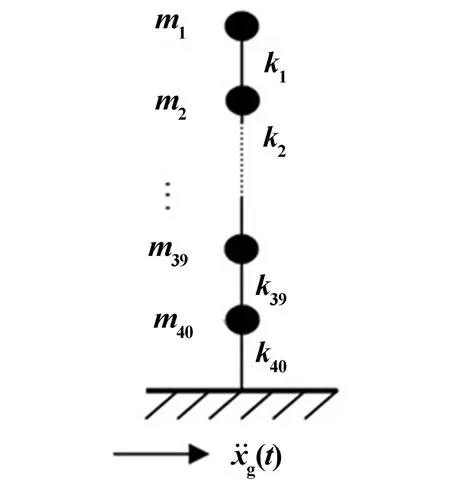
图3 剪切型杜芬系统Fig.3 Shear type MDOF Duffing system

为了验证计算精度,采用本文提出的时域显式迭代算法的计算结果与10000个地震时程样本的蒙特卡罗模拟进行了对比.时间步长取Δt=0.05,迭代收敛相对误差取为0.001%.限于篇幅,仅给出第一个自由度的位移标准差和加速度标准差的结果,分别如图4 和图5所示,EIA表示本文显式迭代算法的计算结果,MCS表示蒙塔卡罗模拟结果.从图中可以看出,当荷载强度因子S0从0.01变化到0.05时,二者吻合都非常好,最大误差只有1.22%.此外,当S0=0.05时,迭代收敛曲线如图6所示,最大迭代步数只有三次.为了对比计算效率,与算例1相同配置的电脑上进行计算,本文显式迭代算法的计算效率远远高于蒙塔卡罗模拟,具体结果见表2.

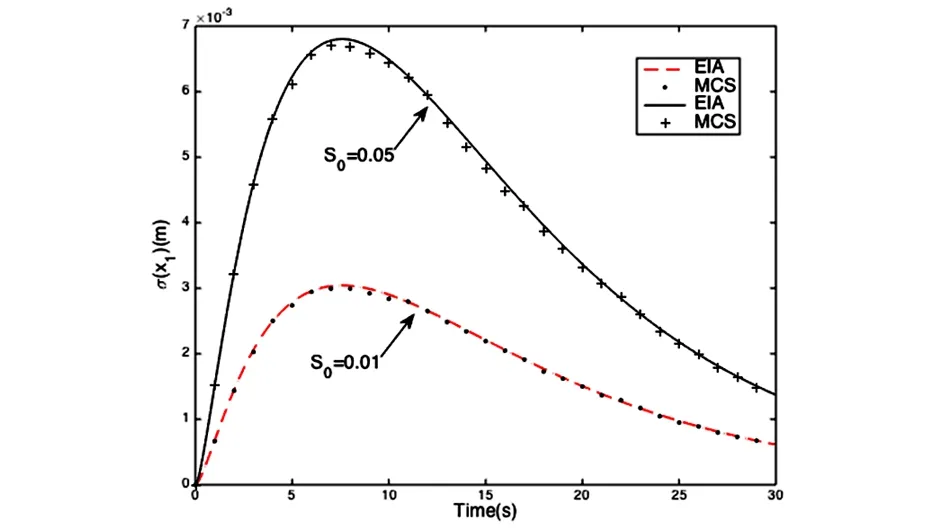
图4 位移X1的标准差Fig.4 Standard deviation of displacement X1

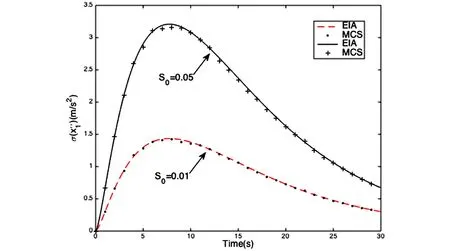
图5 加速度1的标准差Fig.5 Standard deviation of acceleration 1

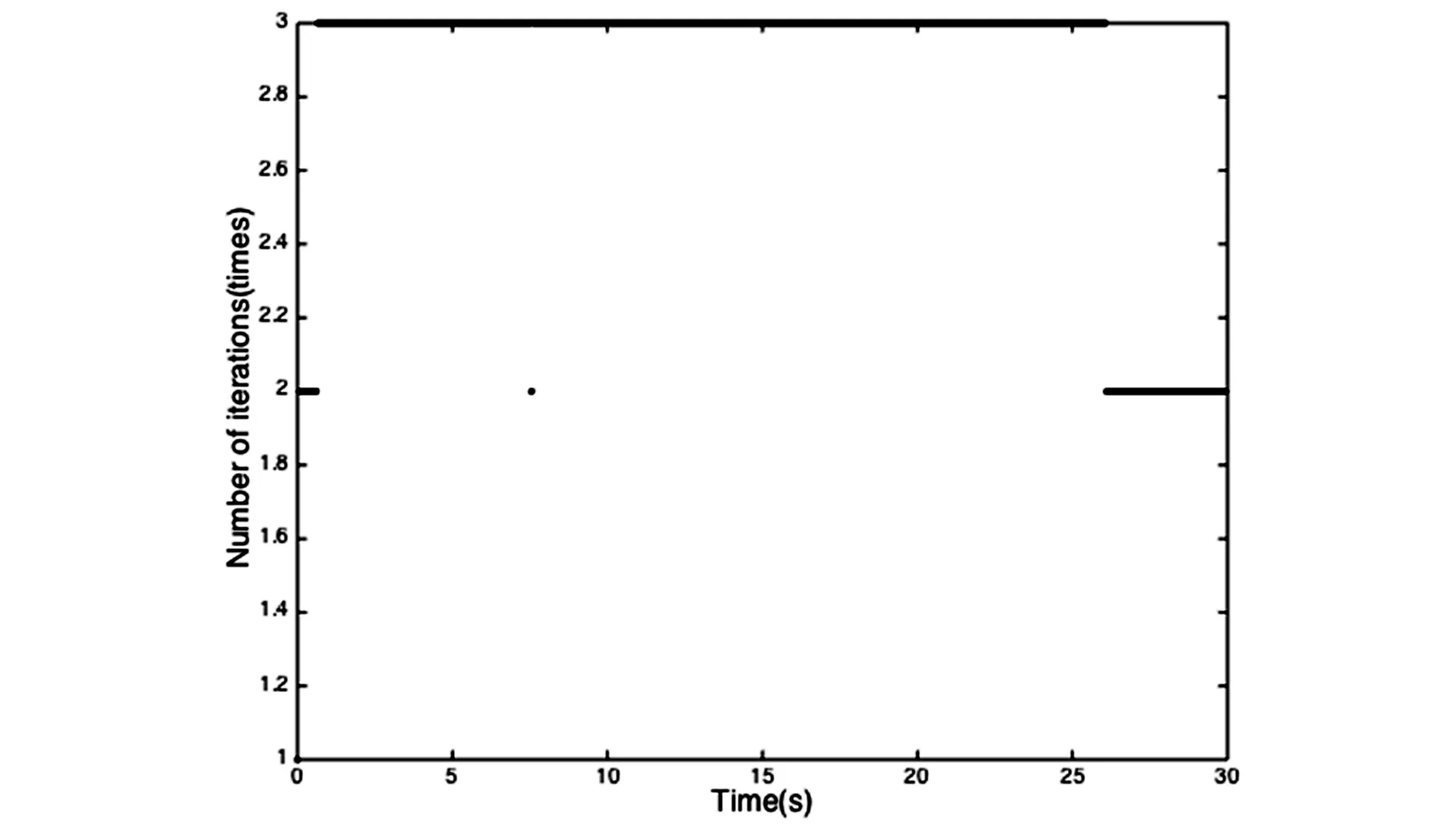
图6 收敛迭代次数曲线Fig.6 Curve of iteration number

表2 蒙塔卡罗模拟与显式迭代算法的效率对比

4 结论

本文基于等效线性化法,提出了一种求解非线性系统非平稳随机响应的时域显式迭代数值算法.该算法可以快速求解多自由度非线性系统在非平稳随机荷载下的均值和协方差.计算效率高是因为以下几方面原因：(1)荷载协方差可以提前计算和储存；(2)当前时刻迭代过程中只需保存两个矩阵,且下一时刻矩阵更新时直接覆盖上一时刻的矩阵,大大节省计算内存.(3)当前时刻的迭代是基于上一时刻的收敛解,显著提高了收敛速度；(4)基于Newmark-β积分格式推导的显式表达式无条件稳定,积分步长可以取的相对较大.因此,该方法非常适合用来求解多自由度非线性系统在非平稳随机荷载下的随机响应.

1Lin Y K. Probabilistic Theory of structural dynamics, Huntington, New York, 1976

2Kiureghian A D, Neuenhofer A. Response spectrum method for multi-support seismic excitations.EarthquakeEngineering&StructuralDynamics, 1992,21(8):713～740

3Soong T T, Grigoriu M. Random vibration of mechanical and structural systems. Prentice Hall, Englewood Cliffs, New Jersey, 1993

4林家浩,张亚辉. 随机振动中的虚拟激励法. 北京:科学出版社, 2004 (Lin Jiahao, Zhang Yahui. Pseudo-excitation method of random vibration. Beijing: Science Press, 2004 (in Chinese))

5Caughey T K, Ma F. The excite steady-state solution of a class non-linear stochastic systems to stochastic excitations.ASMEJournalofAppliedMechanics, 1982,17:137～1426Zhu W Q, Yang Y Q. Exact stationary solutions of stochastically excited and dissipated integrable Hamiltonian systems.ASMEJournalofAppliedMechanics, 1996,63(2):493～500

7Zhu W Q. Exact solutions for stationary responses of several classes of nonlinear systems to parametric and/or external white noise excitations.AppliedMathematicsandMechanics, 1990,11(2):165～175

8Li J, Chen J B. The probability density evolution method for analysis of dynamic nonlinear response of stochastic structures.ACTAMechanicSonica, 2003,35(6):716～722

9Roberts J B, Spanos P D. Random vibration and statistical linearization. John Wiley & Sons, 1990

10 Thomas K, Caughey T. Equivalent linearization techniques.JournalofAcousticalSocietyofAmerica, 1963,35(11):1706～1711

11 Schu⊇ller G I, Pandey M D, Pradlwarter H J. Equivalent linearization in engineering practice for a seismic design.JournalofProbabilisticEngineeringMechanics, 1994,9(1):95～102

12 Iwan W D, Mason A B. Equivalent linearization for systems subjected to non-stationary random excitation.InternationalJournalofNonlinearMechanics, 1980,15:71～82

13 Crandall S H. A half-century of stochastic equivalent linearization.StructuralControlHealthMonitor, 2006,13:27～40

14 Proppe C, Pradlwarter H J, Schu⊇ller G I. Equivalent linearization and Monte Carlo simulation in stochastic dynamics.ProbabilisticEngineeringMechanics,2003,18(1):1～15

15 Lin J H, Wang J, Zhang Y H. Non-stationary random response of MDOF Duffing systems.ShockandVibration, 2004,11(5-6):615～624

16 Marano G C, Acciani G, Fiore A, et al. Integration algorithm for covariance non-stationary dynamic analysis of SDOF systems using equivalent stochastic linearization.InternationalJournalofStructuralStabilityandDynamics, 2015,15(2):1450044

17 苏成,徐瑞.非平稳随机激励下结构随机振动时域分析法. 工程力学, 2010,27(12):77～83 (Su C, Xu R. Random vibration analysis of structures subjected to non-stationary excitations by time domain method.EngineeringMechanics, 2010,27(12):77～83 (in Chinese))

18 苏成,徐瑞. 非平稳随机激励下结构体系动力可靠度时域解法. 力学学报, 2010,42(3):512～520 (Su C, Xu R. Time-domain method for dynamic reliability of structural systems subjected to non-stationary random excitations.ChineseJournalofTheoreticalandAppliedMechanics, 2010,42(3):512～520 (in Chinese))

19 Su C, Xu R. Random vibration analysis of structures by a time-domain explicit formulation method.StructuralEngineering&Mechanics, 2014,52(2):239～260

20 Hu Z Q, Su C, Chen T C, et al. An explicit time-domain approach for sensitivity analysis of non-stationary random vibration problems.JournalofSoundandVibration, 2016,382:122～139

21 Newmark N M. A method of computation for structural dynamics.JournalofEngineeringMechanicsDivision, 1959,85(3):67～94

*The project supported by the National Natural Science Foundation of China (11002056) and the Fundamental Research Funds for the Central Universities (SCUT) (2014220071)

† Corresponding author E-mail: cvchsu@scut.edu.cn

25 March 2017,revised 18 April 2017.

EXPLICIT ITERATION ALGORITHM FOR NON-STATIONARY DYNAMICS RESPONSE ANALYSIS OF EXPLICIT ITERATION ALGORITHM OF NON-STATIONARY STOCHASTIC DYNAMIC RESPONSE ANALYSIS BASED ON EQUIVALENT STOCHASTIC LINEARIZATION*

Li Xueping Wang Kun Wei Peng Su Cheng†

(StateKeyLaboratoryofSubtropicalBuildingScience,SchoolofCivilEngineeringandTransportation,SouthChinaUniversityofTechnology,Guangzhou510000,China)

An efficiency explicit iteration algorithm for non-linear systems subject to non-stationary stochastic seismic excitation is proposed based on the equivalent linearization. Firstly, the nonlinear systems are transformed into the discrete linear systems using equivalent linearization method. And the explicit time-domain iteration algorithm is then deduced based on the Newmark-βintegration method. The proposed algorithm is finally applied to a MDOF Vander-Pol system and a MDOF Duffing system under random non-stationary process. The results verify the high accuracy and efficiency of the proposed explicit iteration procedure.

nonlinear systems, non-stationary, stochastic, equivalent linearization, explicit iteration algorithm

*国家自然科学基金资助项目(11002056) 和中央高校基本科研业务费项目(2014ZZ0071)

10.6052/1672-6553-2017-032

2017-03-25收到第1稿,2017-4-18收到修改稿.

† 通讯作者 E-mail: cvchsu@scut.edu.cn