天琴计划轨道构型长期漂移特性分析

万小波，张晓敏，黎明

航天东方红卫星有限公司，北京100094



天琴计划轨道构型长期漂移特性分析

万小波，张晓敏*，黎明

航天东方红卫星有限公司，北京100094

为了实现天琴计划航天器轨道构型的长期稳定漂移并满足轨道构型的稳定性指标，文章应用优化算法搜索航天器初始最优瞬时轨道要素。建立考虑摄动情况下航天器轨道动力学模型，对导致等边三角形轨道构型发生长周期漂移的轨道要素进行了分析，并且将这些要素作为轨道设计的待优化参量，应用粒子群(Particle Swarm Optimization，PSO)智能寻优算法进行优化，应用最终优化得到的轨道要素进行轨道构型仿真。仿真结果表明，在不进行轨道控制的情况下，4年内轨道构型呼吸角变化小于1.5°，臂长变化小于1 500 km，臂长变化速率小于10 km/s，初步满足轨道构型的稳定性指标。

天琴计划；轨道构型；长期漂移；稳定性；粒子群优化算法

引力波是爱因斯坦广义相对论的四大预言之一[1]，被认为是时空的涟漪。直接证明引力波的存在意义重大，引力波的直接观测是对爱因斯坦广义相对论的最直接验证，同时提供了一种除电磁辐射和粒子辐射之外观测宇宙的新手段或新方法，进而发展引力波天文学。因此直接证明引力波的存在是历代科学家多年的夙愿。

受地面系统噪声及臂长的限制，地基引力波探测系统只能探测到高频的引力波信号[2]。因此在宇宙空间建设探测系统开展低频引力波信号的探测成为科学家的首选，典型代表有欧洲航天局LISA/eLISA计划[3]。中国科学家也提出了类似的引力波空间探测计划，比较典型代表有天琴计划[4]。天琴计划是由中山大学为首的科学家团队发起的空间激光干涉引力波探测项目，该项目计划在距离地球约105km高度的同一近圆轨道面内放置航天器S1、S2、S3，各个航天器之间相位角相差120°，3颗航天器形成等边三角形；在引力波探测期间，由于航天器运行轨道受到各种摄动因素的影响，该等边三角形构型会发生变化，然而引力波探测激光对准子系统、激光稳频子系统、多普勒频移测量子系统对等边三角形构型的稳定性提出限制要求[5]，如果等边三角形构型稳定性超出指标要求，这些子系统的功能将下降或者无法工作，此时航天器需要经过轨道机动使得等边三角形构型满足稳定性指标要求，但是在航天器进行轨道机动期间内，引力波探测任务将被中断，这很可能错过潜在的引力波源信号，因此，空间引力波探测任务要求等边三角形轨道构型在尽可能长的时间内满足稳定性指标要求；综上所述，对于空间引力波探测任务来说，设计和分析航天器的初始瞬时轨道要素，使得航天器组成的三角形轨道构型在尽可能长的任务期间内满足等边三角形的稳定性指标要求是必不可少的工作。

航天器S1、S2、S3对应不同的初始瞬时轨道要素，其形成的等边三角形轨道构型有着不同的长周期漂移特性，而航天器轨道受到的摄动是影响等边三角形轨道构型长周期漂移特性的主要因素，与此前空间科学性卫星试验计划不同的是，比如重力测量卫星,天琴计划的轨道高度约为105km，远远高于重力测量卫星的轨道高度，在分析重力测量卫星轨道摄动时，主要考虑地球的摄动项[6]，而在分析天琴计划航天器轨道摄动时主要考虑三体摄动，忽略地球自身的摄动。文献[7]基于天琴计划引力波探测任务要求，初步对上述等边三角形的稳定提出限制要求，本文主要通过设计和分析航天器初始瞬时轨道要素，从而对等边三角形轨道构型的长周期漂移特性展开分析研究，为后续开展天琴计划相关任务提供借鉴作用。

1 建立模型

1.1 问题描述

天琴计划与其他空间激光干涉引力波探测计划不同的是，天琴计划探测确定的引力波源信号，该引力波源是RXJ0806.3 +1527，其在天球赤道惯性坐标系的位置如图1所示，图1中S代表太阳，E代表地球，地球绕太阳运行的黄道面、天球赤道面之间夹角为23°26′，S1、S2、S3表示3颗大尺度分布式航天器，航天器S1、S2、S3在同一轨道面内以相位角相差120°形成等边三角形。

在设计航天器S1、S2、S3初始轨道要素之前，首先必须知道3颗航天器平均轨道要素的数值大小；根据天琴计划所要探测的引力波源特性和位置信息，文献[8]给出航天器S1、S2、S3平均轨道要素的数值大小如表1所示。

由前述可知，S1、S2、S3航天器轨道在运行时，三者形成等边三角形构型，在空间引力波探测期间，探测信号的精度和分辨率分别对两干涉臂长的差量、两条干涉臂之间夹角即呼吸角的变化量，以及干涉臂两端航天器相对速度的大小提出严格的要求，这3项指标要求均反映了上述等边三角形构型的稳定性，故称之为表征等边三角形稳定性要素，如表2所示。

表1 航天器S1、S2、S3平均轨道要素

表2 表征等边三角形稳定性要素指标要求

本文基于表1航天器S1、S2、S3平均轨道要素，以保证天琴计划探测器在不进行轨道控制的状态下，尽可能长时间的连续工作为目标，分析了系统的长周期漂移特性，确定了航天器初始瞬时轨道要素。

1.2 卫星轨道动力学模型

对于天琴计划，10万公里高的轨道，考虑的轨道摄动因素应包括地球J2项、月球和太阳引力摄动项，以及太阳光压摄动项，但是引力波探测系统有一个无拖曳控制系统，专门用来消除系统受到的非保守力，因此太阳光压不予以考虑。考虑地球J2项、月球和太阳引力摄动项，航天器i在地心赤道惯性坐标系下轨道动力学方程可以表示为[9]：

(1)

(2)

式中：Re为地球平均半径；J2=1.082 64×10-3。

1.3 表征等边三角形稳定性要素计算公式

天琴计划利用航天器S1、S2、S3形成一等边三角形构型，设该等边三角形的3个顶点为S1、S2、S3；表征等边三角形稳定性要素有臂长Lsisj变化量，两个干涉臂之间夹角θsi的变化量，干涉臂长变化速率vsisj；干涉臂长Lsisj，两个干涉臂之间的夹角θsi，干涉臂长变化速率vsisj的计算公式为：

(3)

(4)

(5)

2 选择待优化参数

计算表征等边三角形轨道构型稳定性要素有如下步骤：

1)已知航天器i初始轨道要素，由经典轨道要素与直角法表示航天器运动之间的转换关系及旋转矩阵[11]可得航天器i在初始时刻地心惯性坐标系下的位置坐标rio和速度坐标vio；

2)由航天器i轨道动力学微分方程式(1)和(2)，应用经典四级四阶R-K法，可求得航天器i在tn时刻的位置坐标ritn和速度坐标vitn；其中航天器轨道动力学微分方程中所考虑的摄动项有地球扁率J2摄动项，月球和太阳引力摄动项；选用的时间系统TDB，月球和太阳的星历JPL DE421[12]，积分初始时刻2 034.01.01，积分的时间跨度4年；

3)由式(2)计算得到的航天器i在tn时刻的位置ritn和速度vitn坐标，带入式(3)～(5)，可得表征等边三角形稳定性要素在tn时刻的数值大小，以此类推，可得表征等边三角形稳定性要素在不同时刻的数值。

由于等边三角形轨道构型的臂长变化速度和呼吸角的变化线性近似依赖于干涉臂长的变化[13]，以下取干涉臂长的变化为研究对象；以表1中航天器S1、S2平均轨道要素作为航天器S1、S2的初始轨道要素，按照步骤1)～3)，计算得到在6个月内航天器S1、S2形成的等边三角干涉臂L12变化曲线如图2所示。

干涉臂的变化有短周期漂移和长周期漂移，短周期漂移是航天器轨道运行周期时间范围内干涉臂有不规则的上下波动变化；长周期漂移是从整体趋势看，随着时间的推移，干涉臂长有递减或者递增的趋势，由图2干涉臂L12的变化曲线可知，干涉臂L12短周期漂移对其臂长变化影响不大，而长周期漂移速度较快，因为在不到一个月的轨道运行期内，干涉臂L12的臂长变化已超出初始臂长的1%，干涉臂L13和L23也有类似的短周期和长周期的漂移特性；天琴计划任务寿命是3～5年，因此对轨道构型有长期稳定漂移的特性要求，由上述分析可知，如果将表1中航天器平均轨道要素作为航天器初始瞬时轨道要素，轨道构型稳定性不满足天琴计划的任务要求，因此，需要重新选择航天器初始轨道要素，降低干涉臂长周期漂移速度，使得干涉臂的变化在尽可能多的漂移状态下满足等边三角形稳定性指标要求。

导致图2中干涉臂L12长周期漂移不断缩减的主要原因是航天器S1、S2的平均轨道要素半长轴am不同，在上述外推法计算航天器轨道的过程中，航天器S1、S2瞬时轨道要素半长轴at的变化曲线如图3所示。

由图3可知，由于轨道动力学摄动因素的影响，航天器S1、S2瞬时轨道要素半长轴at处于不断波动的变化，二者不同，而航天器瞬时轨道要素半长轴at可近似表示[14]：

(6)

(7)

(8)

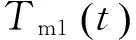
(9)

由上述分析可知，航天器S1、S2轨道平均轨道要素半长轴的不同是导致干涉臂L12长周期递减的主要原因，因此选取航天器S1、S2轨道初始瞬时轨道要素半长轴作为待优化的参数，这是因为航天器初始轨道要素半长轴基本决定了航天器的平均轨道要素半长轴的数值大小，本文通过优化已选择的待优化参数，使得航天器S1、S2、S3形成等边三角形构型在航天器尽可能多的自由漂移状态下满足表2等边三角形稳定性的指标要求。

3 基于PSO参数寻优算法

(10)

式中：x表示空间粒子的位置；v表示粒子的速度，本文粒子位置x的参数为待优化的S1、S2、S3航天器初始瞬时轨道要素半长轴；ω为惯性权重，用来调节粒子速度大小；δ1，δ2为两个学习因子，rand1和rand2为0-1之间的随机数，用来描述种群内部信息交换的学习程度；pi表示该粒子迄今为止最优位置；pg表示该粒子群迄今为止最优位置；下标i表示粒子编号，下标j表示粒子维度，即指粒子向量的长度。

将PSO算法应用到对航天器初始瞬时轨道要素半长轴寻优中需要定义合理的适配度函数；设干涉臂L21或L12为L1，L13或L31为L2，L23或L32为L3，本文选取在一定的数值积分时间内干涉臂L1、L2、L3各个变量的方差之和作为PSO寻优算法的适配值函数H；设积分时间节点为t0,t1,…,tn-1，则Lij表示Li臂在积分时间节点tj处的数值大小，Ai表示干涉臂Li的平均值，表达式为：

(11)

(12)

对上述PSO优化算法用Matlab编程语言实现，程序运行一次只能得到两个优化的参数，以S1、S2航天器为例，在整个PSO优化算法迭代的过程中，S1、S2航天器初始瞬时轨道要素半长轴的收敛情况及适配值函数的变化趋势分别如图4所示。

最后得到S1、S2、S3航天器初始瞬时轨道要素半长轴的最优解为：

(13)

将表1中分布式航天器初始轨道要素半长轴变换为经过优化得到的式(13)数据，航天器其他初始轨道要素不变，然后将变换后表1的数据带入第2节计算表征等边三角形稳定性要素流程中，得到在4年天琴计划任务期间内表征等边三角形稳定性要素的变化曲线。

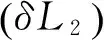
由上述计算的数据可得，在天琴计划4年任务期间内，干涉臂L1、L2、L3臂长变化量δL均符合表2对干涉臂长变化量提出的指标要求。

由上述计算的数据可得航天器S1、S2、S3轨道构型呼吸角在天琴计划4年的任务期间内变化量δθ满足表2对呼吸角的指标要求。

图7为在天琴计划4年的任务期间内，干涉臂L1、L2、L3的臂长变化速率变化曲线，图中干涉臂L1最大臂长变化速率v1max=5.86 m/s；干涉臂L2最大臂长变化速率v2max=5.98 m/s；干涉臂L3最大臂长变化速率v3max=6.11 m/s；由上述数据可知，干涉臂L1、L2、L3最大臂长变化速率均小于9 m/s，满足表2对干涉臂臂长变化速率的指标要求。

4 结束语

以中国空间激光干涉引力波探测天琴计划为研究对象，依据航天器S1、S2、S3轨道构型稳定性的指标要求，首次以数值方法初步进行探测器轨道的设计与分析:

1)建立105km轨道高度的航天器轨道动力学微分方程；

2)分析研究导致等边三角形臂长长周期漂移的轨道要素，然后将此轨道要素作为航天器设计的待优化参数；

3)基于粒子群(PSO)智能优化算法对已选择的待优化参数进行寻优，最后将优化得到的轨道要素进行轨道仿真。结果表明等边三角形的稳定性在长时间漂移下满足指标要求，证明了该方法的有效性。

本文的研究成果能够为未来开展空间引力波探测提供建议与参考。

References)

[1] 子仁，白珊，边星，等.空间激光干涉引力波探测[J]. 力学进展，2013，43(4)：415-447.

LUO Z R，BAI S，BIAN X，et al. Space laser interferometer gravitational wave[J].Advances in Mechanics，2013，43(4)：415-447(in Chinese).

[2] KRZYSZTOF，BELCZYNSKI，DANIE E，et al. The first gravitational-wave source from the isolated evolution of two stars in the 40-100 solar mass range[J]. Nature，2016，534(7608)：512-515.

[3] STEBBINS R T.Rightsizing LISA[J].Classical and Quantum Gravity,2009,26(9):25-28.

[4] LUO J，CHEN L S，DUAN H Z，et al. Tian Qin：a space-borne gravitational wave detector[J].Classical and Quantum Gravity,2015,33(3):12-30.

[5] THEODORE H S. An end-to-end trajectory description of the LISA mission[J]. Classical and Quantum Gravity，2005，22(10)：429-435.

[6] 覃政，张立华，丁延卫. SST-LL重力测量卫星轨道分析[J]. 航天器工程，2014，21(3)：23-27.

QIN Z，ZHANG L H，DING Y W. Analysis of SST-LL gravity exploring satellite orbit[J]. Spacecraft Engineering，2014，21(3)：23-27 (in Chinese).

[7] 万小波，张晓敏. 天琴计划轨道稳定性分析[C]∥五院航天动力学论坛第二届学术研讨会论文集.北京：中国空间技术研究院，2016：28-273．

WAN X B，ZHANG X M. Analysis of Tian Qin mission orbital stability[C]. The collection of the second symposium of space dynamics forum. Beijing：China Academy of Space Technology，2016：：28-273 (in Chinese)．

[8] 耿长福.航天器动力学[M].北京：中国科学技术出版社，2006：387-393.

GENG C F. Spacecraft dynamics[M]. Beijing：China Science and Technology Press，2006：387-393 (in Chinese).

[9] 章仁为.卫星轨道姿态动力学与控制[M].北京：北京航空航天大学出版社，1998：157-176.

ZHANG R W. Dynamics andcontrol of satellite orbit and attitude[M]. Beijing：Beijing University of Aeronautics and Astronautics Press，1998：157-176 (in Chinese) .

[10] 颜庆津.数值分析[M]. 北京：北京航空航天大学出版社，2006：184-185.

YAN Q J. Numerical analysis[M]. Beijing：Beijing University of Aeronautics and Astronautics Press，2006：184-185 (in Chinese) .

[11] 肖业伦. 航天器飞行动力学[M]. 北京：中国宇航出版社，1995.

XIAO Y L. Spacecraft flying dynamical principle[M]. Beijing：China Astronautics Press，1995(in Chinese) .

[12] JPL DE421 Ephemeris[EB/OL].[2015-10-05].ftp：∥ssd.pl.nasa.gov/pub/eph/export/usrguide.

[13] 唐文林. 中国空间引力波探测计划卫星轨道设计的初步研究[D]. 北京：中国科学院大学，2014.

TANG W L. Preliminary study of the orbit design of the Chinese mission to detect the gravitational wave in space[D]. Beijing：Chinese Academy of Science，2014(in Chinese).

[14] 刘林，胡松杰，王歆. 航天动力学引论[M]. 南京：南京大学出版社，2006：80-84.

LIU L，HU S J，WANG X. Introduction to Aerospace Dynamics[M].Nanjing：Nanjing University Press，2006：80-84(in Chinese).

[15] 孙增圻，邓志东，张再兴，等. 智能控制理论与技术[M]. 北京：清华大学出版社，2011：400-420.

SUN Z Q，DENG Z D，ZHANG Z X，et al. Intelligent control theory and technology[M]. Beijing：Tsinghua University Press，2011：400-420(in Chinese).

(编辑：车晓玲)

Analysis of long-period drift characteristics for orbit configuration of the Tianqin Mission

WAN Xiaobo，ZHANG Xiaomin*，LI Ming

DFHSatelliteCo.LTD.，Beijing100094，China

In order to realize the long-term steady drift of Tianqin Mission′s orbital configuration and meet stability index, initial optimum instantaneous orbital elements were searched by the optimization algorithm. Firstly，orbital dynamics model considering perturbation was set up. Secondly,the orbital configuration of equilateral triangle drifted for long-period by the orbital elements′ variety was researched and the orbital elements leading to the orbital configuration of equilateral triangle drifted in a long-period were made as parameters to be optimized. Particle swarm intelligent optimization algorithm (PSO)was applied to optimize parameters selected for optimization. Finally,the simulation results show that the arm length changes less than 1 500 km，the breath angle changes less than 1.5 degrees and the velocity of the arm length variety changes less than 10 m/s in natural drifting of four years without orbital maneuver. The results meet the initial indicators of the orbital configuration.

Tianqin Mission；orbital configuration；long-term drift；stability；particle swarm optimization

10.16708/j.cnki.1000-758X.2017.0044

2017-03-17；

2017-04-18；录用日期：2017-05-18；网络出版时间：2017-05-31 09:59:12

http:∥kns.cnki.net/kcms/detail/11.1859.V.20170531.0959.005.html

万小波(1990-)，男，硕士研究生，873806425@qq.com，研究方向为航天器轨道优化与设计

*通讯作者：张晓敏(1971-)，男，研究员，zhangxiaomin01@tsinghua.org.cn，研究方向为航天器轨道动力学与控制

万小波，张晓敏，黎明. 天琴计划轨道构型长期漂移特性分析[J].中国空间科学技术，2017，37(3)：110-116.

WANXB，ZHANGXM，LIM.Analysisoflong-perioddriftcharacteristicsfororbitconfigurationoftheTianqinMission[J].ChineseSpaceScienceandTechnology，2017，37(3)：110-116(inChinese).

V412.4

A

http:∥zgkj.cast.cn