二氧化碳探测仪瞬态热分析模型修正
李强,陈立恒
1.中国科学院 长春光学精密机械与物理研究所,长春 130033 2.中国科学院大学,北京 100049
二氧化碳探测仪瞬态热分析模型修正
李强1,2,陈立恒1,*
1.中国科学院 长春光学精密机械与物理研究所,长春 130033 2.中国科学院大学,北京 100049
为实现碳卫星载荷在轨温度的准确预测,对其试验状态瞬态热分析模型的修正进行研究。先比较热分析计算结果与热平衡试验结果,求出两者对应温度监控点的温差;再利用蒙特卡洛法对二氧化碳探测仪热分析模型参数进行灵敏性分类,将模型参数分为整体灵敏、局部灵敏与不灵敏参数。然后根据热平衡试验数据,用拉丁超立方和单纯形法的混合法对模型各个参数进行分层修正,得到满足目标函数各个灵敏性参数的最优值。最后将参数最优值代入热分析模型计算验证该修正方法正确性,并进行残差分析。结果显示修正后各温度监控点热分析计算与热试验温差δa小于±0.5℃,残差修正率θ高于80%,修正后多数温差比修正前减少了一个数量级。结果表明修正取得的效果明显,修正方法合理可行。
CO2探测仪;模型修正;热平衡;热分析;灵敏性分类;蒙特卡洛法;分层修正
CO2观测卫星是中国首颗二氧化碳监测卫星,项目隶属于国家科技部863计划设置的“全球CO2监测科学实验卫星与应用示范”重大项目[1],卫星的研制填补了中国大气CO2浓度遥感监测的多项空白。CO2探测仪作为主要载荷之一,可实现对CO2浓度的高精度(4mg/L)监测。CO2探测仪的热分析计算采用节点网络法,而由于航天器内部换热的复杂性,采用节点网络法计算得到的温度值与航天器热平衡试验结果和飞行温度遥测结果都存在偏差[2],通常的做法是利用航天器热平衡试验温度数据修正热分析模型,使之可以正确指导热控实施和准确预测航天器在轨温度。
随着航天器热控精度的提高以及航天器系统结构的日趋复杂,传统的模型修正方法很难满足修正要求,一种基于蒙特卡洛法采用大量重复抽样试验来近似求解问题的修正方法广泛应用到空间热分析模型修正领域中去。文献[3]利用蒙特卡洛及混合法对一卫星稳态模型进行了参数敏感性分析与修正,取得了不错的修正效果;文献[4]利用分层修正的方法对小卫星瞬态热分析模型进行了修正,修正过程中建立了瞬态温度时均量和波动量,解决了瞬态温度时域过程描述问题;文献[5]基于拉丁超立方抽样及等级相关性分析,将元器件表面温度与自身功率进行线性拟合,高效修正了PCBA热模型;文献[6]运用多软件联合修正方法对发热电阻热分析模型进行修正,将首次修正的结果作为二次修正的初始条件,提高了修正精度。以上文献针对热分析模型的修正虽然取得了一定的效果,但修正的模型不是稳态就是结构简单的卫星系统,修正参数也不超过10个,而实际卫星系统结构十分复杂,表面属性、热耦合参数多达几十甚至上百个,因此上述文献的工程应用意义不大。
本文修正的CO2探测仪模型基于I-DEAS/TMG环境,具有结构复杂、修正参数多、参数取值范围量级差异大等特点;同时,探测仪试验状态按照入轨飞行状态及工况模拟,所受空间热环境复杂。这些困难都是稳态热分析模型修正不具备的,国内目前还没有针对此类热分析模型提出有效的修正方法。针对以上修正难点,本文创新性地利用优化方法及分层修正的思想修正探测仪在试验状态下的瞬态热分析模型,修正取得了较好效果,具有很好的工程应用价值。
1 热分析计算与热平衡试验结果 对比
1.1 热分析计算
热设计中,利用有限元仿真软件I-DEAS/TMG模块画出试验状态下CO2探测仪瞬态热分析模型,模型中冷板和热管采用水平安装方式,均与试验状态一致,如图1所示。为保证热分析计算模型的边界条件与热平衡试验相同,模型添加了红外加热笼并按照试验不同区域进行外热流模拟。模型选取壳单元类型,手动划分了8 265个壳单元,采用设置热耦合的方式简化结构,共设置了186个热耦合。同时,为监控探测仪各载荷及安装面温度,在热分析计算模型上设置了温度控制单元,表1为模型主要温度监控区域与相应单元代号。热分析计算中考虑两种极端工况,分别为冬至时刻成像模式高温工况和夏至时刻成像模式低温工况。

温控区域温度监控单元红外成像电箱TC1A/B分束系统蒙皮TC2A星敏支架安装面TC2B望远镜框架TC3A主框架靠近CAPI安装面TC3B定标指向电箱TC4A/B主框架光栅罩TC5A主框架成像镜筒TC5B探测器遮光罩TC6A/B主框架安装点TC7-A、B、C、D760nm可见探测器TC8A/B1610nm红外探测器TC9A/B2060nm红外探测器TC10A/B红外成像电箱安装面MC3定标指向电箱安装面MC4
1.2 热平衡试验
CO2探测仪的热平衡试验利用空间环境模拟器模拟探测仪所处太空环境,采用红外加热笼模拟外热流,其他试验装置包括卫星平台模拟装置、温度测量设备、温度控制设备、热控电箱及综合仿真设备、电源等,热平衡试验的装置示意及试验现场如图2所示。
对应热分析计算中的计算工况,热平衡试验的工况分为高温工况和低温工况,根据国军标[6]中对稳态热平衡试验平衡判据中的规定,4 h内温度波动要小于±0.5℃。本热平衡试验中,以主框架温度监控点TC2A/B,TC3A/B,TC5A/B及TC7A、B、C、D的温度为判据,将上述温度监控点高、低温试验工况的平衡温度绘制成曲线,如图3所示。
1.3 误差分析
在试验结束后,对试验结果进行整理,在整理的过程中剔除个别无效数据,排除人为疏忽错误等原因对试验数据精确性的影响,之后需要对试验本身误差进行分析。地面热平衡试验的误差来源主要是真空模拟误差、空间冷黑背景模拟误差、外热流模拟误差及安装面边界条件模拟的误差。
对于热平衡试验而言,真空的模拟只需要排除空间环境模拟器内空气的对流和导热的影响即可。因此从工程应用的角度讲,用1×10-3Pa的压力来模拟宇宙空间的高真空,空气对流和导热对热平衡试验的影响完全可以忽略[7]。相关计算[8]表明,当热沉温度达到100 K,热沉表面发射率为0.90时,对于常温范围的航天器,热平衡试验的温度相对误差小于1%,因而冷黑背景模拟带来的误差也可以忽略不计。
CO2探测仪热平衡试验中外热流采用热流计进行反馈,安装面温度边界条件则是通过铂电阻进行反馈,两者在测量时都会存在一定的误差,这种误差很小,模拟出来外热流和安装面温度即使在±20%的拉偏工况也不会对探测仪各温度监控点造成影响。综上所述,本次CO2探测仪热平衡试验可靠程度较高,试验数据真实有效。
1.4 结果对比
由于CO2探测仪各温度监控点的控温精度较高,且瞬态热分析模型中每个温度监控点的温度值以轨道周期的均值表示,因此热分析计算与热平衡试验的温差应不大于±0.5℃,以保证设计精度。
对CO2探测仪热分析计算结果和热平衡试验数据进行处理,取热分析计算温度监控单元轨道周期99 min内的温度时均值作为对比对象一,取样点为300个;取热平衡试验达到稳态4 h内温度监控点的平均试验温度作为对比对象二,以热试验测得温度为真值,计算出热分析计算结果偏离热试验数据的程度,以两者温差的绝对值表示,相应温度监控点的对比结果如表2所示。
由表2可以看出,高温工况下偏差较大的温度监控点主要集中在TC3B、TC6A/B、TC8A/B,其中偏离程度最大的为温度监控点TC6A/B,温差为7.85℃。低温工况下偏差较大的温度监控点主要集中在TC2A、TC5A、TC8A/B,其中偏离程度最大的为温度监控点TC5A,温差为4.73℃;高、低温工况误差较大的温度监控点各不相同,给模型修正工作增加了难度。
2 参数灵敏度分析
在进行修正之前,需要对热模型中的热设计参数进行整理和分析,本文修正的CO2探测仪热分析模型的热设计参数众多,因此有必要在修正之前对这些热设计参数进行灵敏度分析。灵敏度分析在航天器热设计领域已经得到了广泛的应用[9-12],找出对模型温度灵敏度高的参数进行重点修正,可以很好地提高修正效率与结果的准确性。
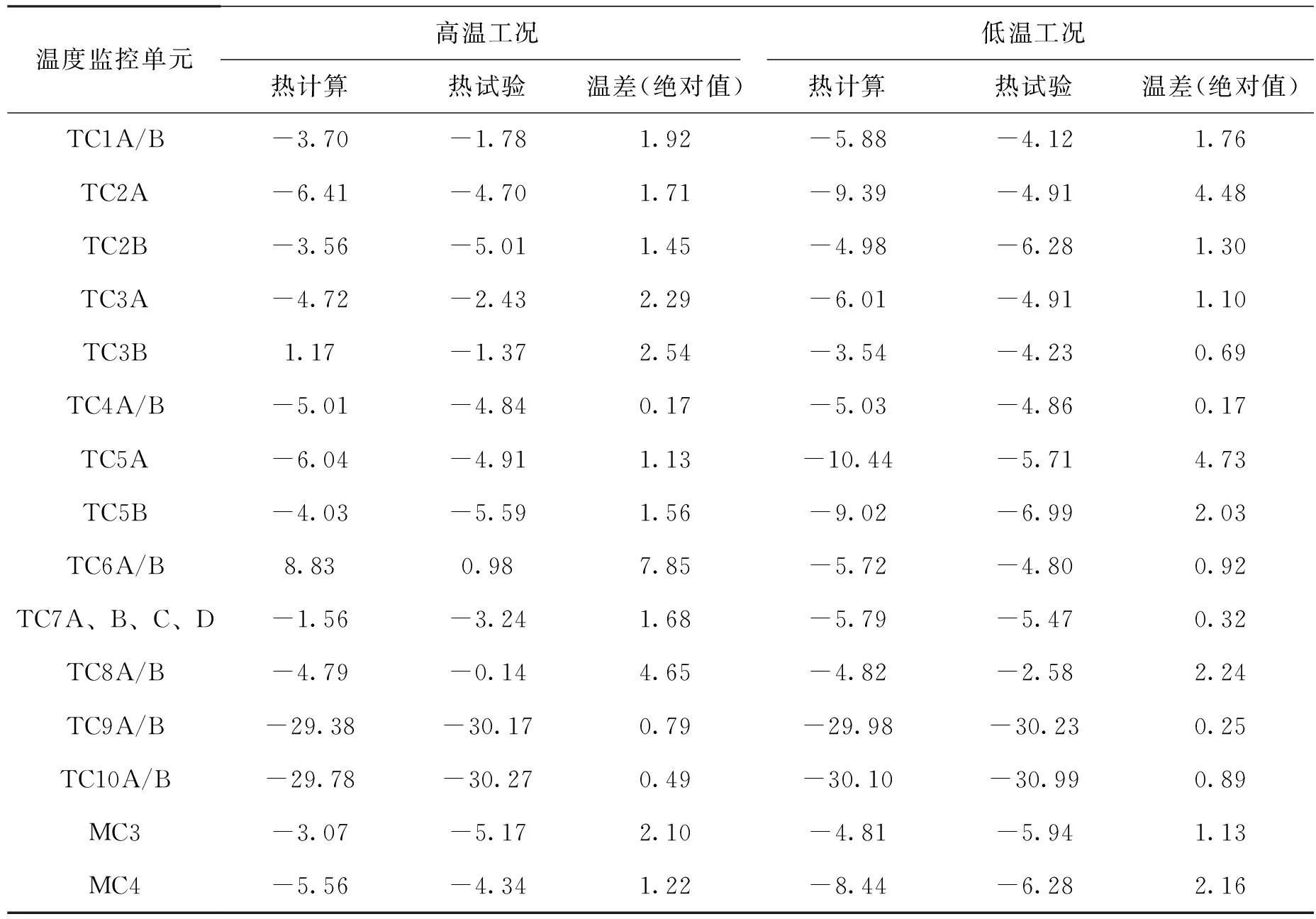
表2 温度监控点结果对比
2.1 修正参数灵敏性分类
对CO2探测仪模型的热设计参数进行整理,选出可能的关键参数共26个,包括散热面喷涂的SR107-ZK白漆吸收率、多层隔热材料(Multi-Layer Insulation,MLI)表面包覆的F46膜表面发射率和吸收率、多层MLI等效辐射换热系数及探测仪不同部件之间的传导热阻。由于抽样的参数过多,需要对这些热设计参数进行灵敏性分类。根据模型温度场对参数的灵敏程度,将参数划分为整体灵敏、局部灵敏和不灵敏参数,文献[13]详细介绍了利用蒙特卡洛法对热设计参数进行敏感性分析的方法,各参数对热设计的灵敏度即为监控点温度与参数的相关系数,利用Spearman等级相关系数公式表示[14]:
(1)
式中:N为抽样次数;Xi为热设计参数抽样值;Yi为监控点温度值;O(Xi)表示对N次抽样参数值进行升序或降序排列时,Xi的排列序号;O(Yi)表示对N次抽样温度值进行升序或降序排列时,Yi的排列序号。

(2)
(3)

2.2 灵敏度分析结果
利用MATLAB实现在参数各自的取值范围内进行蒙特卡洛抽样,并将抽样的结果进行随机组合,代入热分析软件I-DEAS计算出各温度监控点的温度结果。取抽样次数N=500次,待分析参数26个,用字母A~Z表示,取15个温度监控点一个轨道周期内的温度计算结果进行整理,计算得到各类参数的灵敏度分析结果散点图,如图4所示。

3 模型修正及结果
对所有参数进行灵敏度分类之后,采用分层修正的思想[15-17],对整体灵敏性参数及局部灵敏性参数进行修正。即先修正对热分析计算结果影响较大的整体灵敏性参数,得到整体灵敏性参数的初步最优值;再以上一步修正的最优值作为初始条件,修正局部灵敏性参数,进一步得到局部灵敏性参数的初步最优值;最后,在前两步修正结果的基础上,对所有灵敏性参数进行全局修正,得到所有参数最终的最优值。
3.1 目标函数
以CO2探测仪热平衡试验高低温工况数据为依据,分别修正对应的热分析模型。在建立修正目标函数时,同样采用瞬态热分析模型时域温度变化考查试验数据与计算结果间的偏差。以残差修正率θ来描述修正效果,其计算公式如下:
(4)
式中:δa表示修正后热分析计算与热平衡试验对应温度监控点的温差;δb表示修正前的温差。θ越大,修正效果越好。
以所有温度监控点残差修正率的均值最大为模型修正的目标函数,单个温度监控点温度时域变化内残差修正率及目标函数OBJECT的定义如下:
(5)
(6)
式中:M为单个轨道周期温度取样点数目,这里与前面同取为300;tTi为取样点试验温度;t0i为修正前取样点初始计算温度;tci为迭代时取样点计算温度;N为温度监控点个数15。利用目标函数的最优求解得到所有灵敏性参数的最优值组合。
3.2 修正方法
采用拉丁超立方(Latin Hypercube Sampling,LHS)和单纯形法相结合的混合法对各个灵敏性参数进行搜索。LHS是蒙特卡洛法抽样方法的改进方法,它将N维抽样空间的每一维均分成M份,抽样时保证在每一份内随机抽样一次,M即为抽样次数,抽样空间由一个M×N矩阵构成,每个抽样点等概率地分布在抽样空间内。在修正的初期,与蒙特卡洛法抽样相比,LHS方法具有更好的抽样覆盖率及更高的效率,节省了试验成本和时间,有效地避免了大量反复抽样。
单纯形法是一种直接优化方法,其不需要计算目标函数一阶导数,只需计算各点的函数值就能进行迭代寻优,因此具有程序简单、收敛速率快、效果好的特点。根据问题的维数N,选取由N+1个定点构成的单纯形,在修正后期以LHS抽样确定的参数最优值组合作为单纯形初始顶点,求出这些定点处的目标函数并加以比较,确定函数值较大的顶点和函数值下降方向,寻找到新的较好的点替换该点,构成新的单纯形。经过若干次迭代可以求出满足收敛准则的极小值点。图5为采用混合法的分层修正流程。
3.3 修正结果
将三次分层修正后得到的各灵敏性参数的最优值组合带入到I-DEAS/TMG软件中进行计算,得到修正后的模型热分析计算结果,以分析修正效果。表3为热分析模型各灵敏性参数修正的最终结果,利用修正后的热分析模型进行计算,得到高、低温工况温度监测点修正后的计算结果。表4为两工况各温度监测点修正前后热分析计算与热平衡试验的温差对比,以公式(4)中修正前温差δb和修正后温差δa的绝对值作为比较对象,并计算出各个温度监控点的残差修正率θ。
从表3、表4的数据可以得出结论,利用分层思想及混合法对CO2探测仪热分析模型整体灵敏性参数及局部灵敏性参数的修正取得较好的效果;表4显示的各温度监控点修正后热计算与热试验的温差均小于±0.5℃,所有温度监控点残差修正率θ均高于80%,多数温度监控点的温差修正后比修正前减小了一个数量级。
在高温工况和低温工况中分别选取两个修正前后温差较大且受关注的温度监控点,高温工况选取温度监控点TC3B,因为该点的温度值在热分析计算中接近主框架温控指标的上临界温度-1℃;低温工况选取温度监控点TC5A,因为该点的温度值在热分析计算中接近主框架温控指标的下临界温度-9℃。

表3 各参数修正结果
图6、图7分别为两个主框架温度监控点在三次分层修正过程中轨道周期99min内的温度变化曲线,图中显示每次修正后热分析计算温度曲线都更接近于热平衡试验,且第一次修正的效果最明显,随后两次的修正效果变小,间接表明了修正整体灵敏性参数对模型温度影响大于局部灵敏性参数。

表4 各温度监控点修正前后温差对比
4 结束语
利用拉丁超立方法和单纯形法的结合方法与之前热分析模型修正相比可以很好地提高修正效率和修正精度,特别是针对瞬态及结构复杂的热分析模型,结果显示这种混合法取得很好的修正效果,为同类热分析模型修正提供了较好的参考价值。
修正时引入灵敏度分类和分层修正思想,进一步减少了修正的时间成本,结果同时表明,针对整体灵敏性参数对模型的影响要高于其他参数,修正温度后热分析计算与热试验温差缩小了1℃左右,修正效果比修正其他参数明显,因而在以后热分析模型修正中,对模型温度影响较大的参数应当进行重点修正。
References)
[1] 李毅,吴清文,陈立恒,等. 二氧化碳探测仪的热控系统[J]. 光学 精密工程,2015,23(4):1053-1061.
LI Y,WU Q W,CHEN L H,et al. Thermal control system of carbon dioxide detection instrument[J]. Optics and Precision Engineering,2015,23(4):1053-1061(in Chinese).
[2] 程文龙,刘娜,钟奇,等. 卫星稳态热模型参数修正方法研究[J].宇航学报,2010,31(1):270-275.
CHENG W L,LIU N,ZHONG Q,et al. Study on parameters correction method of steady-state thermal model for spacecraft[J]. Journal of Astronautics,2010,31(1):270-275(in Chinese).
[3] 张镜洋,常海萍,王立国. 小卫星瞬态热分析模型修正方法[J]. 中国空间科学技术,2013,33(4):24-30.
ZHANG J Y,CHANG H P,WANG L G. Correction method for transient thermal analysis model of small satellite[J].Chinese Space Science and Technology,2013,33(4):24-30(in Chinese).
[4] 王开山,李传日,郭恒晖,等. 基于相关性分析的PCBA热力学模型修正[J].装备环境工程,2014,11(5):119-124.
WANG K S,LI CH R,GUO H H,et al. Study on the method of thermodynamics model updating of printed circuit board assembly[J]. Equipment Environment Engineering,2014,11(5):119-124(in Chinese).
[5] 施道云,杨光,张卫国,等. 基于Isight/Fluent联合仿真的热模型修正方法研究[J].科学技术与工程,2016,16(4):205-209.
SHI D Y,YANG G,ZHANG W G,et al. Thermal model modifying based on the combination of Isight and Fluent[J]. Science Technology and Engineering,2016,16(4):205-209(in Chinese).
[6] 国防科工委. GJB1033A-2005 航天器热平衡试验方法[S].北京:中国标准出版社,2005:1-20(in Chinese).
[7] 侯增祺,胡金刚.航天器热控制技术——原理及应用[M].北京:中国科学技术出版社,2007:420-421.
HOU Z Q,HU J G. Spacecraft thermal control technology——principles and applications[M]. Beijing:China Science and Technology Press,2007:420-421(in Chinese).
[8] 丁延卫,卢锷. 航天光学遥感器热环境试验模拟方法的研究[J].光学 精密工程,2003,11(4):24-29.
DING Y W,LU E. Thermal environmental simulation methods of space optical remote sensors[J].Optics and Precision Engineering,2003,11(4):24-29(in Chinese).
[9] HAN Y G,XUAN Y M. Parameter sensitivity analysis for the satellite thermal design[J].Chinese Journal of Computational Physics,2004,21(5):455-460.
[10] 杨化彬,陈立恒,李义,等. 广角极光成像仪滤光片的热设计及试验[J].光学 精密工程,2014,22(11):3019-3027.
YANG H B,CHEN L H,LI Y,et al. Thermal design and verification of transmission filter for wide angle aurora imager[J].Optics and Precision Engineering,2014,22(11):3019-3027(in Chinese).
[11] 郭亮. 基于灵敏度分析的空间高光谱成像仪热控制技术研究[D]. 北京:中国科学院大学,2013:20-22.
GUO L. Study on thermal control technique of space hyperspectral imager based on the sensitivity analysis[D].Beijing:University of Chinese Academy of Sciences,2013:20-22(in Chinese).
[12] 郭亮,吴清文,颜昌翔. 空间光谱成像仪热设计参数的灵敏度[J].光学 精密工程,2012,20(6):1208-1217.
GUO L,WU Q W,YAN C X. Sensitivity of thermal design parameters for space spectral imaging apparatus[J]. Optics and Precision Engineering,2012,20(6):1208-1217(in Chinese).
[13] 刘娜,程文龙,钟奇,等. 基于蒙特卡洛法的卫星热模型参数敏感性分析研究[J]. 航天器工程,2009,18(4):102-107.
LIU N,CHENG W L,ZHONG Q,et al. Sensitivity analysis of spacecraft thermal model based on Monte-Carlo method[J].Spacecraft Engineering,2009,18(4):102-107(in Chinese).
[14] 龚曙明. 应用统计学[M].第2版.北京:清华大学出版社,2005:268-270.
GONG S M. Applied statistics[M.]. 2nd ed. Beijing:Tsinghua University Press,2005:268-270(in Chinese).
[15] 朱跃,张令弥,郭勤涛. 基于分层思想对复杂工程结构的有限元模型修正技术研究[J].振动与冲击,2011,30(12):175-180.
ZHU Y,ZHANG L M,GUO Q T. Finite element model updating technique based on hierarchical method of complex engineering structure[J].Journal of Vibration and Shock,2011,30(12):175-180(in Chinese).
[16] 洪良友,贾亮,吴艳红,等. 航天器结构动力学模型修正方法研究[J]. 强度与环境,2015,42(1):23-30.
HONG L Y,JIA L,WU Y H,et al. Research on systemic method of dynamic model updating concerning aerospace structural[J]. Structure & Environment Engineering,2015,42(1):23-30(in Chinese).
[17] 张青雷,高孟雪. 发电机仿真分析及优化设计[J].电子科技,2016,9(1):56-59.
ZHANG Q L,GAO M X. Finite element analysis and optimization of generator[J].Electronic Sci. &Tech.,2016,29(1):56-59(in Chinese).
(编辑:车晓玲)
Correction for transient thermal analysis model of Carbon Dioxide detector
LI Qiang1,2,CHEN Liheng1,*
1.ChangchunInstituteofOptics,FineMechanicsandPhysics,ChineseAcademyofSciences,Changchun130033,China2.UniversityofChineseAcademyofSciences,Beijing100049,China
In order to accurately predict the on-orbit temperature of the Tan-Sat loading,the research for transient thermal analysis model correction under test conditions was presented. Compared the results between thermal analysis calculation and thermal balance test,temperature differences of the temperature monitors were confirmed. Parametric sensitivity analysis of carbon dioxide detector thermal analysis model was completed by the Monte Carlo method,and model parameters were divided into global sensitive,local sensitive and insensitive parameters. According to the data of thermal balanced test,the Latin hypercube sampling and simplex mixed methods were applied to correct model parameters by the classification layer by layer,and the optimal values were calculated.These values were taken into the thermal analysis model to verify the accuracy of the correction method and analyze the residual error. Correction results show that the corrected temperature differenceδais less than ±0.5℃ for all the temperature monitors, the residual error correction ratesθare greater than 80%,while most temperature differences reduce an order of magnitude after correction.These results illustrate the correction is effective and the method is reasonable and feasible.
carbon dioxide detector; model correction; thermal balance; thermal analysis; sensitivity classification; Monte Carlo method; hierarchical correction
10.16708/j.cnki.1000-758X.2017.0004
2016-07-18;
2016-08-23;录用日期:2017-01-24;网络出版时间:2017-05-31 14:10:57
http:∥kns.cnki.net/kcms/detail/11.1859.V.20170531.1410.011.html
国家“863”计划(2013AA122001)
李强(1990-),男,硕士研究生,Li_qiang119@163.com,研究方向为空间光学遥感器热设计及模型修正
*通讯作者:陈立恒(1978-),男,研究员,硕士生导师,博士,chenliheng3@163.com,研究方向为空间光学遥感器热控技术
李强,陈立恒.二氧化碳探测仪瞬态热分析模型修正[J].中国空间科学技术,2017,37(3):44-52.LIQ,
CHENLH.CorrectionfortransientthermalanalysismodelofCarbonDioxidedetector[J].ChineseSpaceScienceandTechnology,2017,37(3):44-52(inChinese).
V416.5
A
http:∥zgkj.cast.cn

