基于二维工龄更换的保修服务优化研究

李欣玥，高勇民，王维强，司书宾

1.中国华阴兵器试验中心，陕西 华阴 710054

2.西北工业大学 机电学院，陕西 西安 710072

保修服务作为引入承制单位优质技术力量，是辅助军方完成新型测试设备深度修理和重大任务专项保障等工作的唯一途径，其合理性直接决定了能否将承制单位这一地方保障力量最大程度地“嵌入”到装备维修保障系统当中[1]。随着军用装备技术复杂程度的逐渐增高，二维非更新保修策略的应用越来越普及。例如，某光测设备载车发动机的初始保修期限包括日历时间和使用摩托小时两个限制条件，根据保修服务过程中的维修方式可将保修服务分为两类：第一，修复性维修的保修服务；第二，修复性维修和预防性维修的保修服务[2，3]。在二维保修期内若对单元实施预防性维修，则预防性维修间隔期也应是二维的[4，5]。

Huang建立了退化过程服从非奇次泊松过程单元在按比例费用分摊保修策略下的周期性预防性维修贝叶斯决策模型[6]，并利用二元联合分布建立可修单元二维保修服务中的定期预防性维修优化模型[7]。Chien针对故障率增长单元建立了更新保修服务策略下工龄更换间隔期优化模型，研究了不可修产品同时考虑免费更换保修策略和按比例分摊保修策略的解析模型[8，9]，并对不可修产品按比例折扣保修的工龄更换间隔期进行了优化[10]，分析了离散时间过程下定期更换策略对保修服务费用的影响[11]。Wu研究了保修服务期内考虑老化损失的周期性预防维修优化问题[12]。Sana对生产系统的盈利能力进行了研究，允许该系统生产的产品存在一定生产缺陷率，对这些产品进行免费保修服务[13]。Bouguerra对6种维修策略下的延伸保修服务双赢价格区间求解问题开展了建模研究[14]。Aggrawal建立了考虑产品销售周期的保修服务价格模型，在该模型中单元故障寿命服从指数分布[15]。现有二维保修文献大多从成组的更换角度出发并进行保修服务优化研究，对工龄更换下的二维保修建模研究较少。当前，基于工龄更换的二维预防性维修间隔期主要根据专家经验确定，缺少科学的决策依据。传统的一维维修间隔期确定方法无法满足保修服务决策需求，需要对采取二维工龄更换维修的二维保修服务开展建模研究。

1 模型假设

定期更换策略主要包括成组更换策略和工龄更换策略两类。目前，常用的定期更换策略为一维定期更换策略。但随着现在装备单元技术复杂度越来越高，性能越来越先进，很多装备单元的故障规律受多种因素（单元的运行时间、使用时间、行驶里程等）的影响。在对这种装备进行维修时，若只给出关于时间的一维定期更换间隔期会忽略其他影响因素对故障规律的作用，造成维修不及时的情况出现。

二维工龄更换策略是指若单元在使用过程中没有发生故障，则按照规定的二维工龄（日历时间与使用程度）进行定期更换；如果在规定的时间（二维工龄间隔期）内发生故障，则对故障单元进行修复性维修，维修后重新开始对工龄进行计时。工龄更换策略相比定期更换策略具有一定的灵活性。若选择单变量法来描述单元的二维故障规律，则二维工龄更换过程如图1所示。

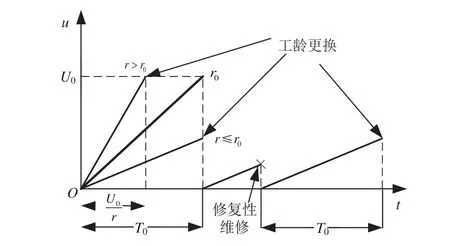
图1 二维工龄更换策略Fig.1 2D age replacement strategy

设二维初始保修期的时间界限和使用程度界限为WB和UB。使用度和时间之间存在线性关系，即单元的使用度u和时间t之间的关系为u=rt，r为使用率。对于不同的设备，r取值不同。设 ，rB=UB/TB。g（r）为使用率r的概率密度函数。二维工龄更换维修为完善维修，间隔期为（T0，U0）。T0是二维工龄更换维修的时间间隔期，U0是二维工龄更换维修的使用度间隔期。不管先到哪个界限，都会执行二维工龄更换维修策略，r0=U0/T0。如果在工龄更换工作之前发生故障，则进行修复性维修工作，单元修复如新，工龄更换周期重新开始计时。Cp为二维工龄更换维修费用，Cm为修复性维修费用，Cd为单位停机损失。Tp表示单元预防性更换所需时间，Tf表示单元故障更换所需时间。CR（t，T0，U0）表示单元以工龄周期（T0，U0）进行维修时，在t时刻内期望保修费用，CR（T0，U0）表示二维非更新保修服务费用。λ（t|r）表示单元在使用率r时的故障率函数，F（t|r）表示单元在使用率r时的累计故障分布函数，R（t|r）表示单元在使用率r时的可靠度函数，其中：

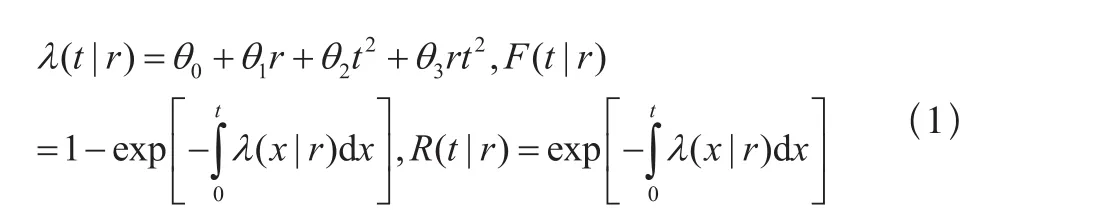
2 模型构建

首先，建立单元的工龄更换周期优化模型。对单元的进行工龄更换时，根据保修期和工龄更换周期之间的关系，可分为r0≤rB和r0＞rB两种情况。

（1）当r0≤rB时，根据r的取值有r≤r0，r0＜r≤rB和r＞rB三种子情况。

当r≤r0时，保修期在WB时刻终止。按照二维工龄更换间隔其中的时间间隔期T0进行工龄更换，可进一步分为 0 ＜ WB≤ Tf，Tf＜ WB≤ T0+Tf和 WB＞ T0+Tf三种情况。

（a）当0＜WB≤Tf时，保修期内将不进行任何的更换活动，所有的费用为故障后产生的损失，此时单元在保修期WB内的期望费用为：

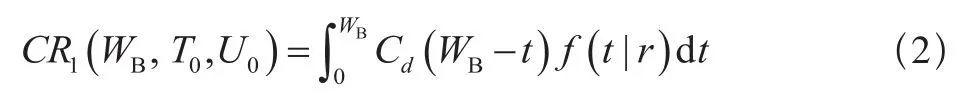
（b）当 Tf＜ WB≤ T0+Tf时，若 t ＜ WB-Tf，则仅进行修复性维修工作，保修费用为：

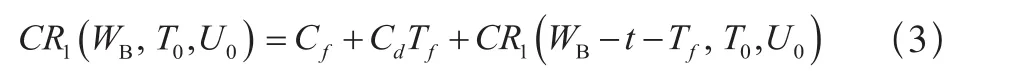
若WB-Tf＜t≤WB，则不进行修复性维修，保修费用为：

因此，此时单元在保修期内的期望费用为：

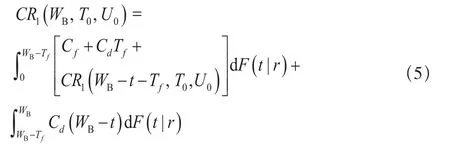
（c）当WB＞T0+Tf时，此时单元在保修期内的期望费用为：

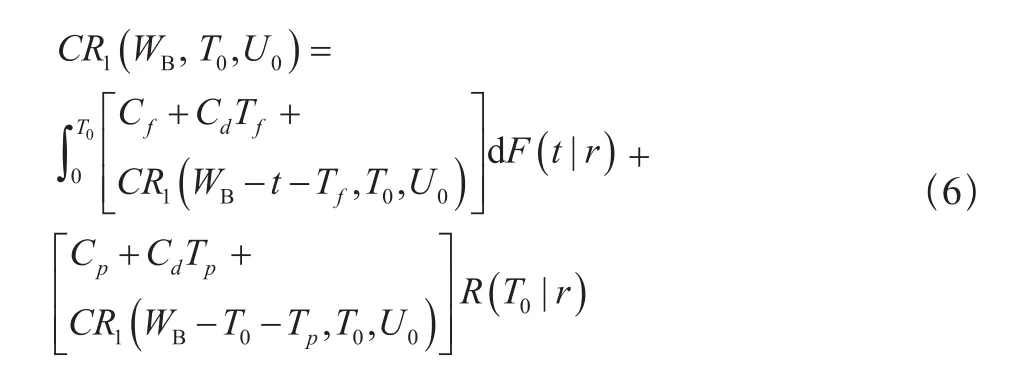
当r0＜r≤rB时，保修期在WB时刻终止。按照二维工龄更换间隔其中的使用度间隔期U0进行工龄更换，可进一 步 分 为 ：0 ＜ WB≤ Tf，Tf＜ WB≤ U0/r+Tf，WB＞ U0/r+Tf三种情况。

（a）0＜WB≤Tf时，保修期内将不进行任何的更换活动，所有的费用为故障后产生的损失，此时单元在保修期内的期望费用为：

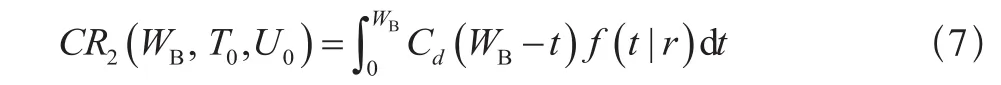
（b）Tf＜ WB≤U0/r +Tf时，若t＜ WB-Tf，则仅进行修复性维修工作，保修费用为：

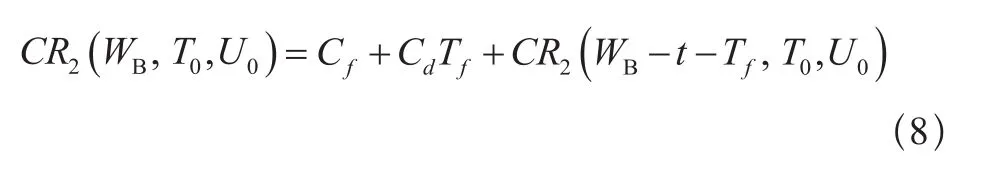
若WB-Tf＜t ≤WB，则不进行修复性维修，保修费用为：

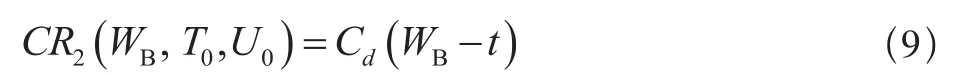
因此，此时单元在保修期内的期望费用为：

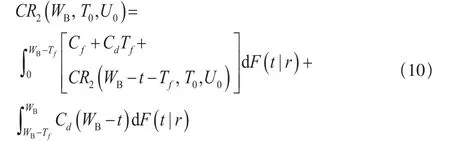
（c）当WB＞UB/r +Tf时，此时单元在保修期内的期望费用为：

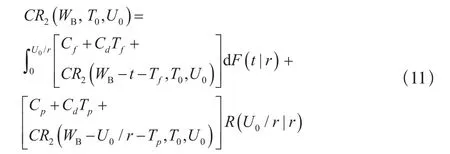
当r＞rB时，保修期在UB终止。按照二维工龄更换间隔其中的使用度间隔期U0进行工龄更换，可进一步分为：0 ＜ UB/r≤ Tf，Tf＜ UB/r≤ U0/r +Tf，UB/r＞ U0/r +Tf三种情况。

（a）当0＜UB/r≤Tf时，保修期内将不进行任何的更换活动，所有的费用为故障后产生的损失，此时单元在保修期WB内的期望费用为：

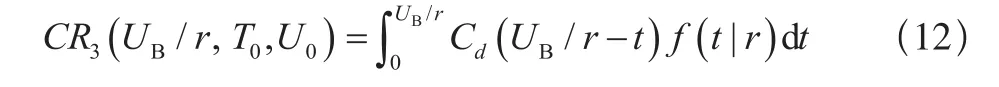
（b）当 时，若 则仅进行修复性维修工作，保修费用为：

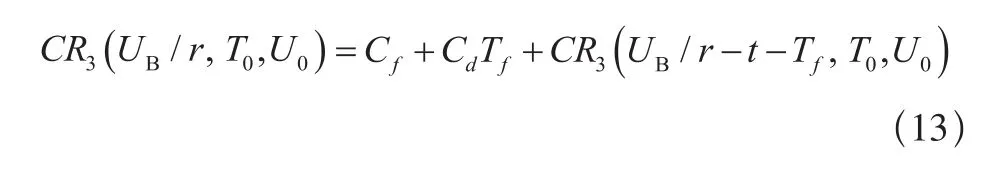
若 ，则不进行修复性维修，保修费用为：

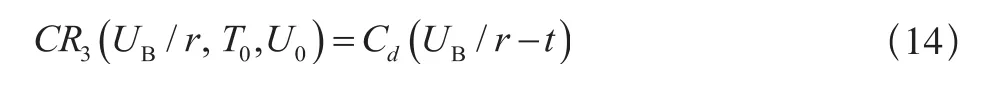
因此，此时单元在保修期内的期望费用为：

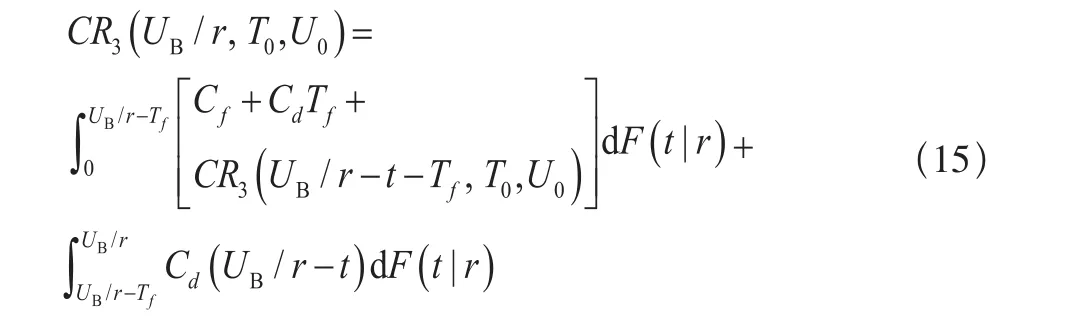
（c）当 时，此时单元在保修期内的期望费用为：

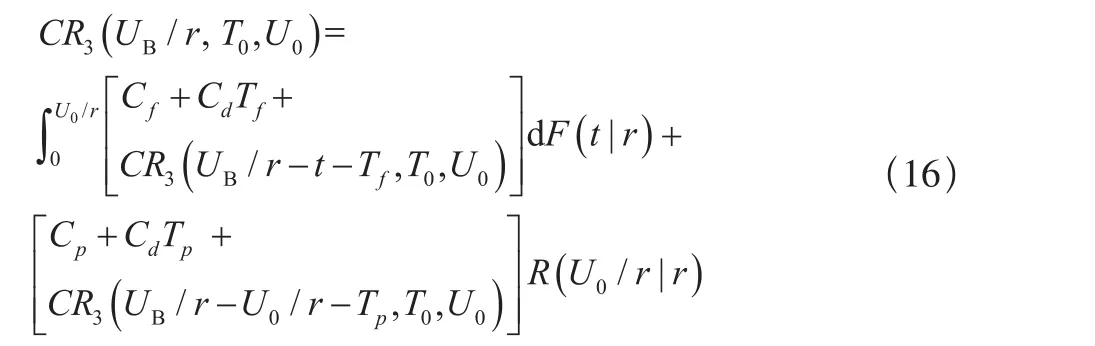
综上所述，当r0≤rB时，考虑工龄更换的二维非更新保修服务费用为：

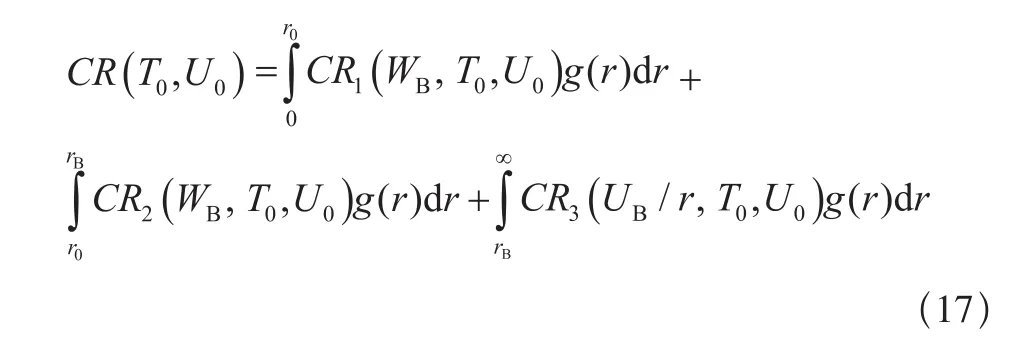
（2）当r0＞rB时，根据r的取值有r≤rB，rB＜r≤r0和r＞r0三种子情况。

当r≤rB时，保修期在WB时刻终止。按照二维工龄更换间隔其中的时间间隔期T0进行工龄更换，可进一步分为 0＜WB≤ Tf，Tf＜WB≤ T0+Tf和 WB＞T0+Tf三种情况。

（a）当0＜WB≤Tf时，保修期内将不进行任何更换活动，总费用为故障后产生的损失，此时单元在保修期内的期望费用为：

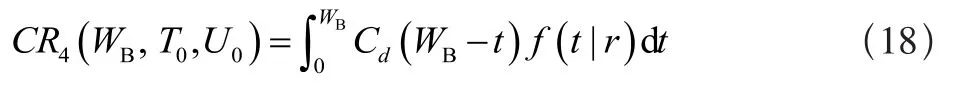
（b）当Tf＜WB≤T0+Tf时，若t＜WB-Tf则仅进行修复性维修工作，保修费用为：

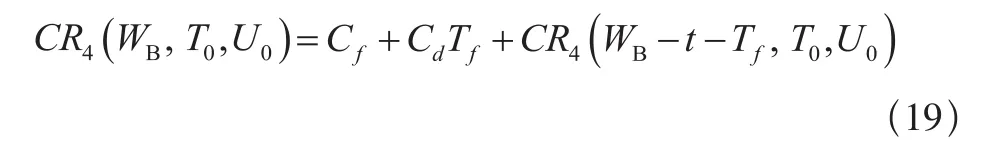
若WB-Tf＜t≤WB，则不进行修复性维修，保修费用为：

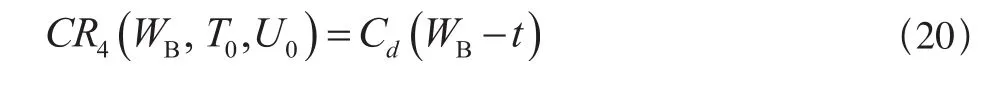
因此，此时单元在保修期内的期望费用为：

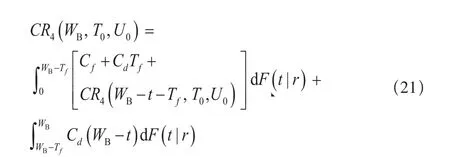
（c）当WB＞T0+Tf时，此时单元在保修期内的期望费用为：

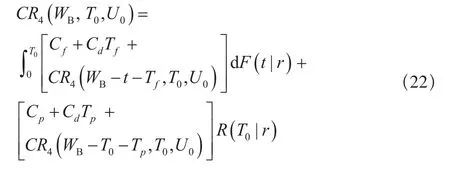
当rB＜r≤ r0时，保修期在UB终止。按照二维工龄更换间隔其中的时间间隔期T0进行工龄更换，可进一步分为0＜UB/r≤Tf，Tf＜UB/r≤ T0+Tf和UB/r＞T0+Tf三种情况。

（a）当0＜UB/r≤Tf时，保修期内将不进行任何的更换活动，所有的费用为故障后产生的损失，此时单元在保修期内的期望费用为：

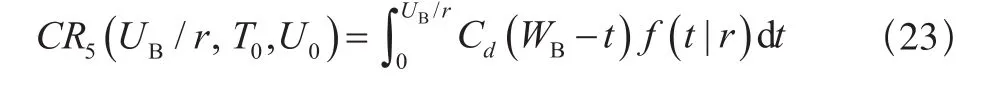
（b）当Tf＜UB/r≤ T0+Tf时，若t＜UB/r -Tf则仅进行修复性维修工作，保修费用为：

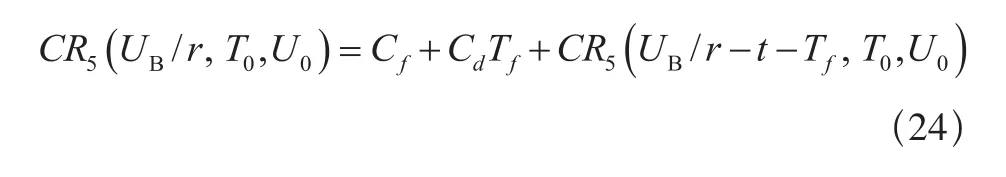
若UB/r-Tf＜t≤UB/r，则不进行修复性维修，保修费用为：

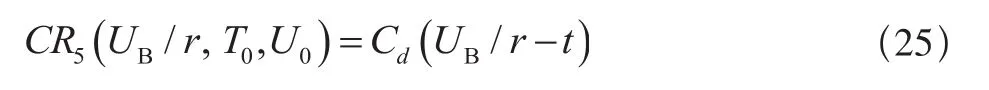
因此，此时单元在保修期内的期望费用为：

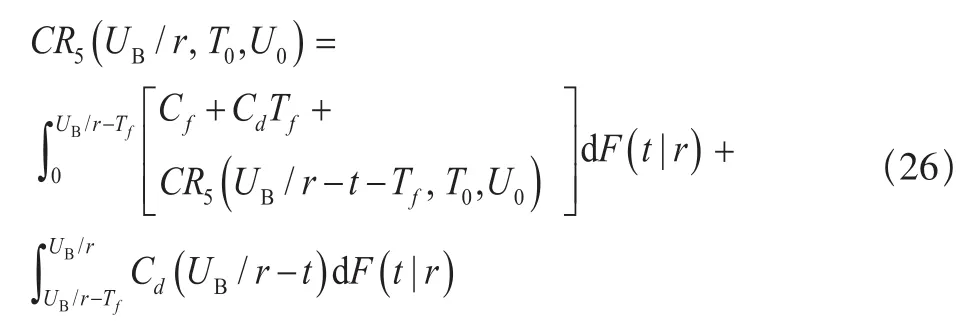
（c）当UB/r＞T0+Tf时，此时单元在保修期内的期望费用为：

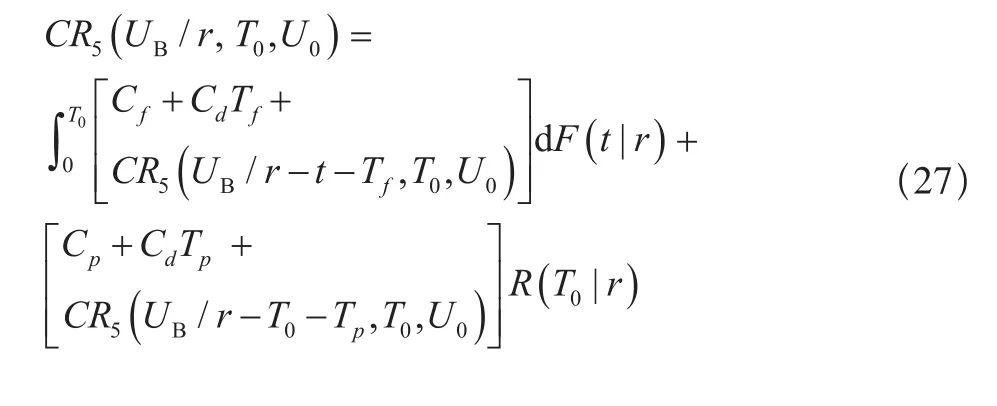
当r＞r0时，保修期在UB时刻终止。按照二维工龄更换间隔其中的使用度间隔期U0进行工龄更换，可进一步分为 0 ＜ UB/r≤ Tf，Tf＜ UB/r≤ U0/r +Tf和 UB/r＞ U0/r +Tf三种情况。

（a）当0＜UB/r≤Tf时，保修期内将不进行任何的更换活动，所有的费用为故障后产生的损失，此时单元在保修期WB内的期望费用为：（28）

（b）当Tf＜UB/r≤U0/r +Tf时，若t＜UB/r-Tf则仅进行修复性维修工作，保修费用为：

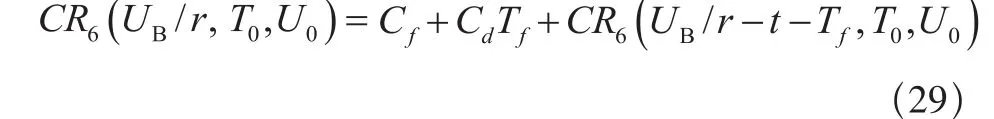
若WB-Tf＜t≤WB，则不进行修复性维修，保修费用为：

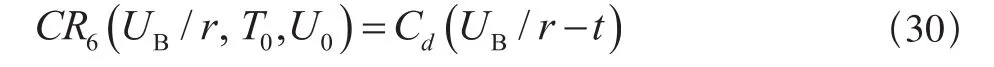
因此，此时单元在保修期内的期望费用为：

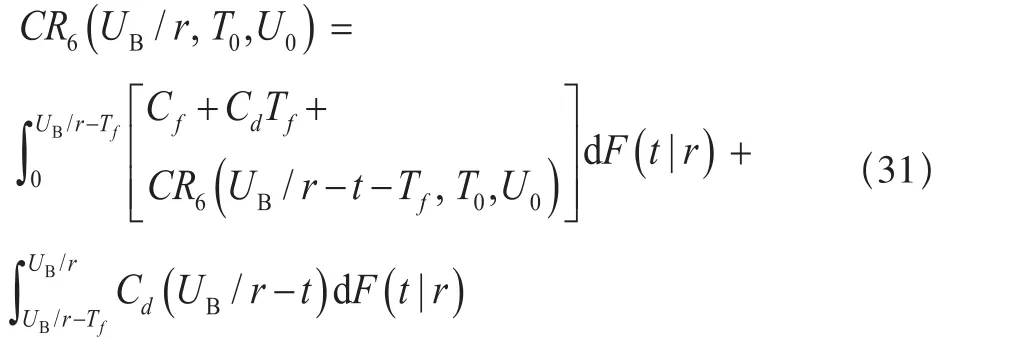
（c）当UB/r＞U0/r +Tf时，此时单元在保修期内的期望费用为：

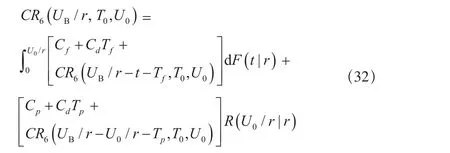
综上所述，当r0＞rB时，考虑工龄更换的二维非更新保修服务费用为：

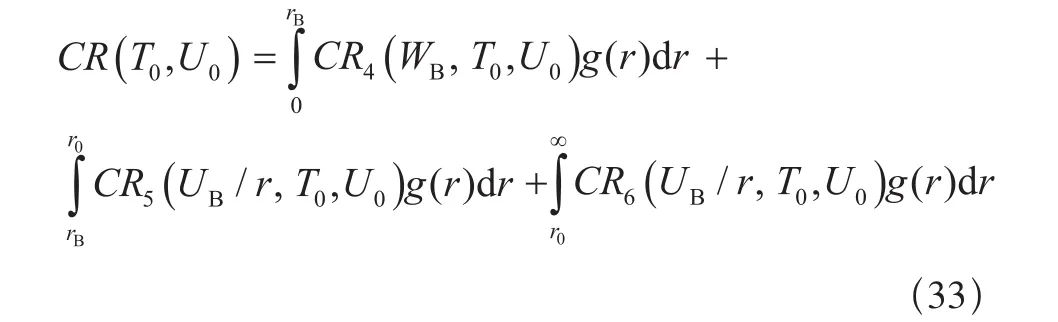
3 算例分析

以某光测设备载车发动机为例进行算例分析。设Cp=500元，Cm=1000元，Cd=200元，Tf=18天，Tp=8天。初始保修服务期为（400 天，80×104km）。θ0=5×10-5，θ1=5×10-5，θ2=10×10-5，θ3=10×10-5。假设使用率 r服从均匀分布、正态分布与威布尔分布。均匀分布的上下限ru=3.05，rl=0.05。正态分布的μ=20000km/年，标准差为σ=1.6，威布尔分布选用两参数威布尔分布，尺度参数m=2，形状参数η=2.5。

当使用率r服从均匀分布、正态分布和威布尔分布时，分别计算每组（T0，U0）所对应保修费用，保修服务费用如图2所示。可以看出，保修服务费用随预防性维修时间间隔期T0和预防性维修使用程度间隔期U0的增加先减小再增大，存在最优点。

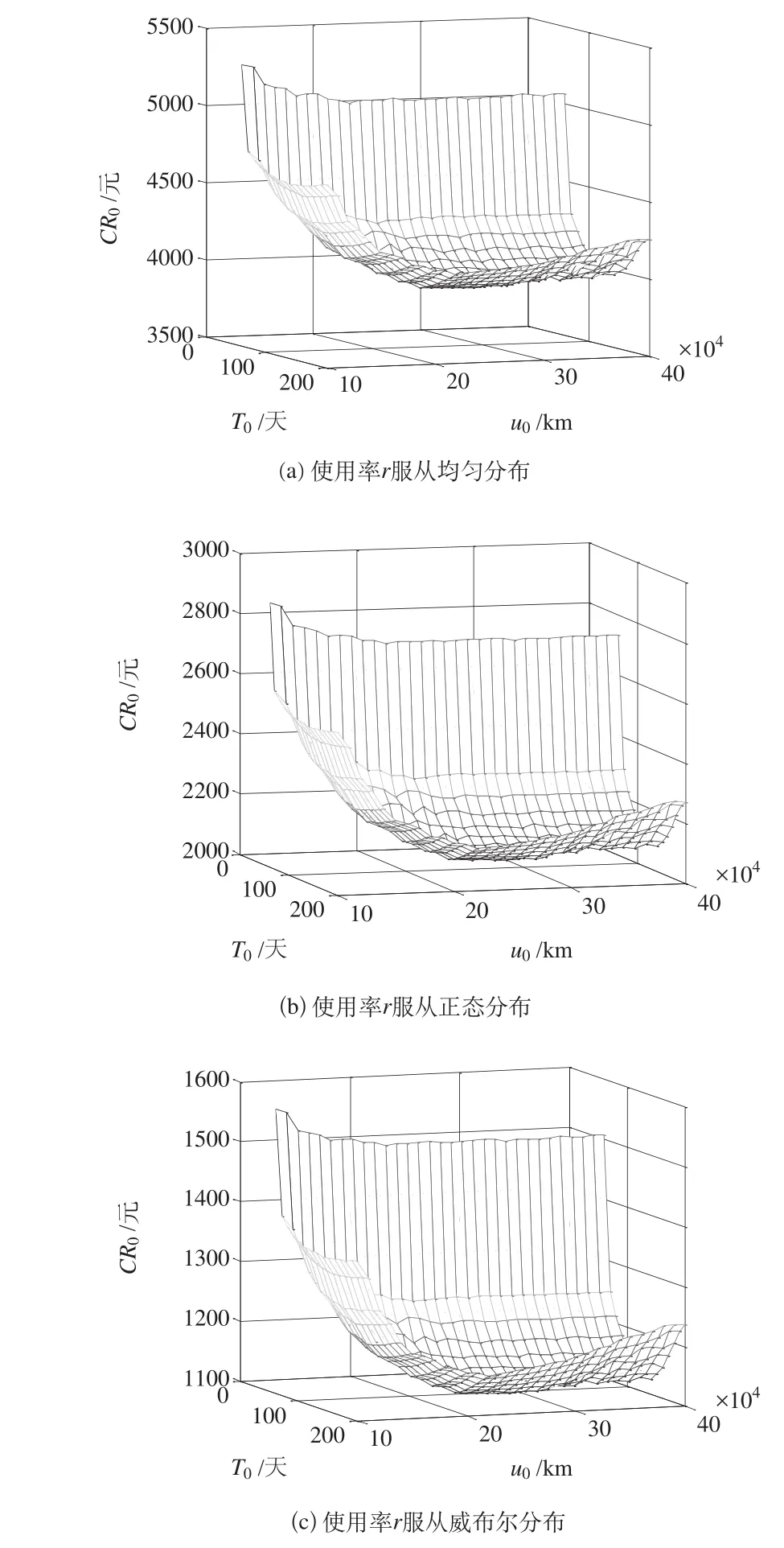
图2 使用率r不同分布下保修费用Fig.2 Warranty cost when r obeys different distribution

为证明在保修期内采取二维工龄更换要优于一维工龄更换，在使用率服从不同分布的情况下，截取二维保修费用最优时的二维曲线与采取一维工龄更换策略的二维非更新保修费用曲线进行对比，如图3～图5所示。从图中可以看出，保修服务费用随二维工龄间隔期和一维工龄间隔期变化的趋势是一样的，都是随着间隔期增加，保修服务费用先减少后增加。通过对比可以看出，二维预防性维修相比一维预防性维修可以有效降低保修服务费用。最优二维工龄更换维修间隔和最优一维工龄更换维修间隔的计算结果见表1。

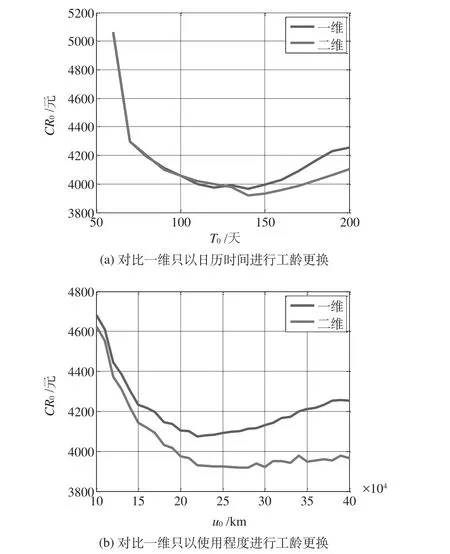
图3 使用率r服从均匀分布下保修服务费用对比Fig. 3 Comparision of warranty cost when r obeys uniform distribution

4 结论

本文以军民融合装备维修保障为背景，结合装备实际需求，利用递归算法建立了考虑二维工龄更换的非更新保修服务策略模型。根据保修期和工龄更换周期之间的大小关系，对模型的两种情况进行讨论，并对模型进行算例分析，结果表明二维工龄更换策略相比一维工龄更换策略可以有效降低二维非更新保修服务费用。研究成果为二维保修策略的实施提供了理论基础，为深入推进军民融合发展提供了理论支持。本文虽然对更新保修建模进行了探索，但在未来的研究中还需对模型进行进一步的扩展研究：考虑不完善维修，保修过程中单元升级维修等问题。

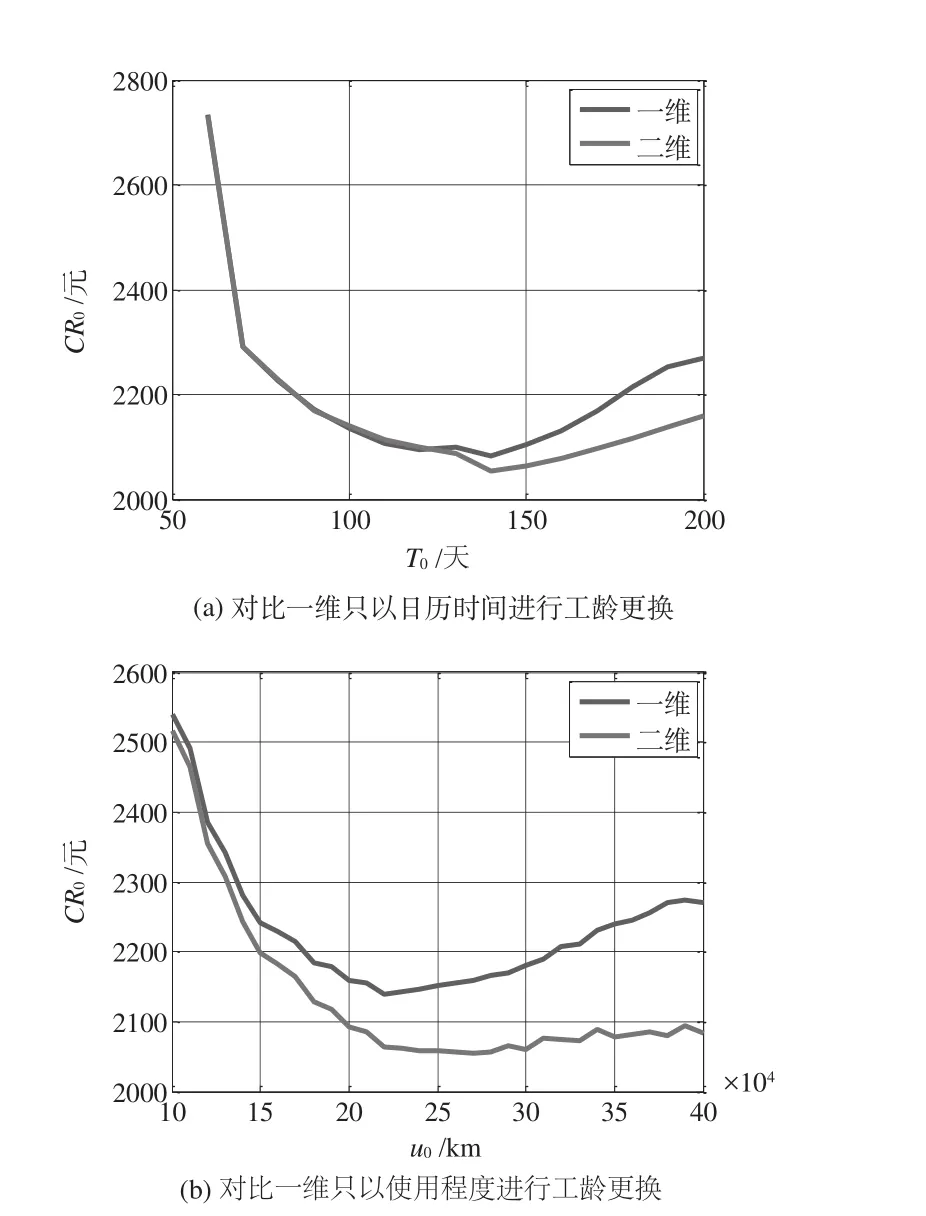
图4 使用率r服从正态分布下保修服务费用对比Fig.4 Comparision of warranty cost when r obeys normal distribution

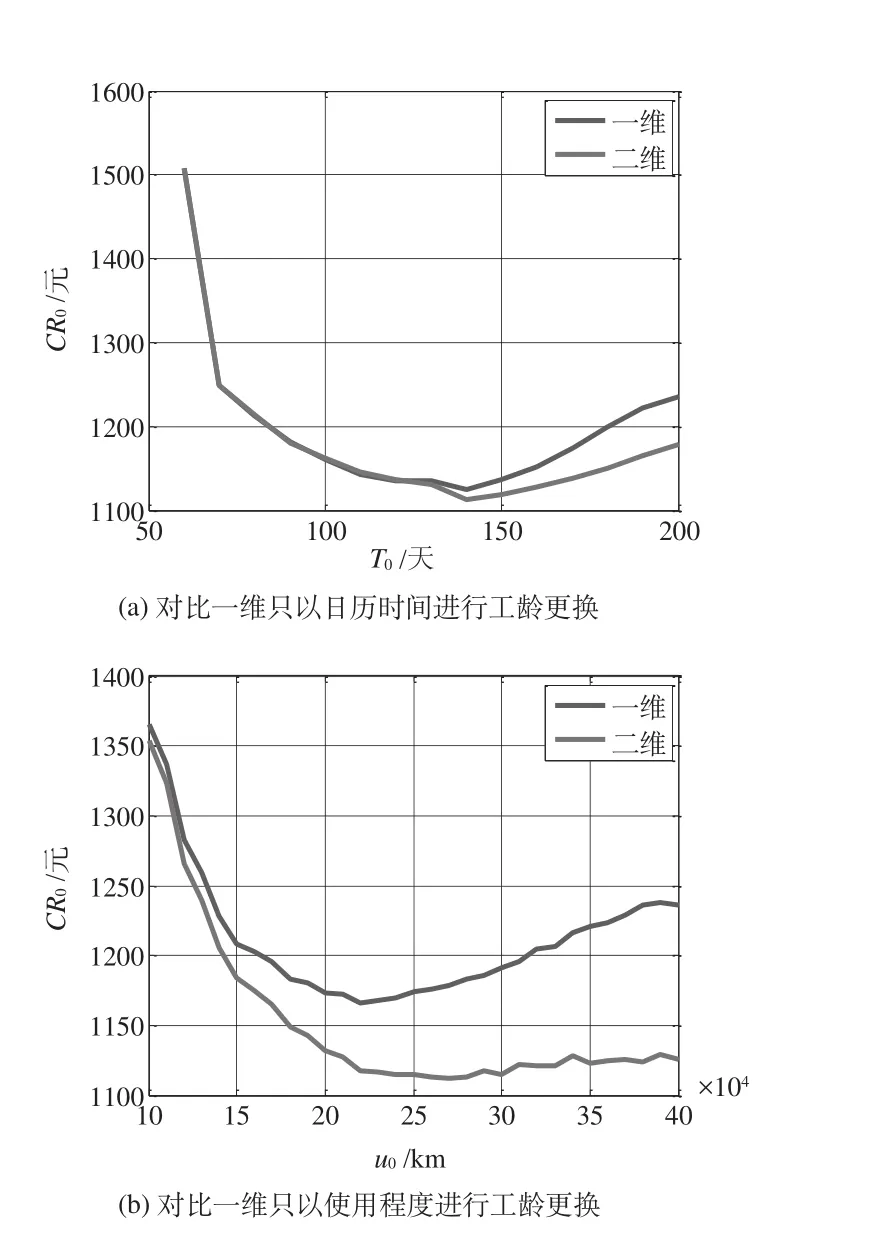
图5 使用率r服从威布尔分布下保修服务费用对比Fig.5 Comparision of warranty cost when r obeys Weibull distribution

表1 保修费用最优值Table 1 Optimal warranty cost

[1] 李欣 ，贾云献，韩玉成，等.军民融合条件下新型军械装备保修模式研究[J].军械工程学院学报，2014，26（3）： 15-20.LI Xinyue， JIA Yunxian， HAN Yucheng， et al. Study on the warranty mode for the new-tech equipment under the condition of military-civil integration[J]. Journal of Ordnance Engineering College， 2014， 26（3）： 15-20. （in Chinese）

[2] Shafiee M， Chukova S. Maintenance models in warranty： A literature review[J]. European Journal of Operational Research，2013， 229（3）： 561-572.

[3] Wu S. A review on coarse warranty data and analysis[J].Reliability Engineering & System Safety， 2013， 114： 1-11.

[4] Blischke W R. Product warranty handbook[M]. Florida： CRC Press， 1995.

[5] Blischke W R. Warranty management and product manufacture [M].London： Springer， 2006.

[6] Huang Y S， Fang C C. A cost sharing warranty policy for products with deterioration[J]. Engineering Management， IEEE Transactions， 2008， 55（4）： 617-627.

[7] Huang Y S， Gau W Y， Ho J W. Cost analysis of twodimensional warranty for products with periodic preventive maintenance[J]. Reliability Engineering & System Safety， 2015，134： 51-58.

[8] Chien Y H. A general age-replacement model with minimal repair under renewing free-replacement warranty[J]. European Journal of Operational Research， 2008， 186（3）： 1046-1058.

[9] Chien Y H. Optimal age for preventive replacement under a combined fully renewable free replacement with a pro-rata warranty[J]. International Journal of Production Economics，2010， 124（1）： 198-205.

[10] Chien Y H. The effect of a pro-rata rebate warranty on the age replacement policy with salvage value consideration[J]. IEEE Transactions on Reliability， 2010， 59（2）： 383-392.

[11] Chien Y H. The effects of a free-repair warranty on the discretetime periodic replacement policy[J]. International Journal of Production Economics， 2012， 135（2）： 832-839.

[12] Wu J， Xie M， Ng T S A. On a general periodic preventive maintenance policy incorporating warranty contracts and system ageing losses[J]. International Journal of Production Economics，2011， 129（1）： 102-110.

[13] Sana S S. Preventive maintenance and optimal buffer inventory for products sold with warranty in an imperfect production system[J]. International Journal of Production Research， 2012，50（23）： 6763-6774.

[14] Bouguerra S， Chelbi A， Rezg N. A decision model for adopting an extended warranty under different maintenance policies[J].International Journal of Production Economics， 2012， 135（2）：840-849.

[15] Aggrawal D， Anand A， Singh O， et al. Prof i t maximization by virtue of price & warranty length optimization[J]. The Journal of High Technology Management Research， 2014， 25（1）： 1-8.