一种基于分布中心的矢量数据零水印算法

吕文清，张黎明

(1.兰州交通大学 测绘与地理信息学院，甘肃 兰州 730070；2.甘肃省地理国情监测工程实验室，甘肃 兰州 730070)

一种基于分布中心的矢量数据零水印算法

吕文清1,2，张黎明1,2

(1.兰州交通大学 测绘与地理信息学院，甘肃 兰州 730070；2.甘肃省地理国情监测工程实验室，甘肃 兰州 730070)

针对鲜有零水印算法能同时适用于点、线、面矢量数据版权保护，提出一种基于分布中心的矢量地理空间数据零水印算法。首先，对矢量数据进行格网划分；其次，计算格网内每个点到其算数平均值中心的距离，并将得到的距离序列与距离平均值进行比较，大于等于距离平均值，则记为1，否则为0；然后，统计格网内的0和1数量的多数，记为0或1，以此生成空间数据特征值；最后，将该特征值与置乱后的二值水印进行异或，构造出零水印图像。实验表明，文中算法能同时适用于点、线、面矢量数据，并且对常见的平移、缩放、裁剪、格式转换、随机删点等攻击鲁棒性好。

矢量地理空间数据；算数平均值中心；零水印；鲁棒性

随着测绘地理信息行业的不断发展，地理空间数据在地理信息、电子导航、数字城市、环境保护等领域得到广泛应用。然而，目前GIS矢量数字产品的市场状况十分混乱[1]，侵犯版权的事件时有发生，传统的版权保护方式已经很难适应目前的需要。一方面，地理空间数据生产成本高昂，精度高，安全级别较高；但另一方面，当前的地理空间数据主要以数字化形式保存，这在为数据拷贝和传播提供便利的同时也使得数据的盗版使用变得极其容易[2]。数字水印技术作为近年来信息安全领域发展起来的前沿技术，在矢量地理空间数据版权保护方面得到了广泛的重视和研究[3-7]。

目前，矢量地理空间数据水印算法主要为空域算法和频域算法，这两种算法都需要改变载体数据来添加水印信息，这在一定程度上影响了数据的质量，对于数据精度要求高的应用领域，可能会造成数据无法正常使用。为了在实现版权保护的同时不损害数据质量，满足对数据高保真的要求，温泉等人首次提出了零水印的概念，并将其应用到数字图像版权保护中[8]。零水印是指不修改原始作品的内容，利用原始作品的重要特征构造水印，能解决水印鲁棒性和不可见性之间的矛盾[9]。张佐理[10]等首次将零水印技术引入矢量地图版权保护领域，通过统计平均分块后各个分块的顶点数，并利用变换和加密构造出水印图；之后一些学者如曹刘娟[11]、孙鸿睿[9,12]等纷纷对矢量地理数据零水印进行了相应的研究，并取得了一些成果。但目前对矢量数据零水印的研究多针对某一特定类型的矢量数据，鲜有零水印算法能同时适用于点、线、面数据版权保护，因此，本文在前人研究的基础上提出了一种同时适用于点、线、面3种矢量数据的零水印算法。

1 零水印构造方案

算法的基本思路：首先对空间数据的最小外接矩形进行平均分块；其次计算每个格网中点到其算数平均值中心的距离和格网内所有距离的平均值；然后，将距离平均值与每个距离进行比较，若某点所对应的距离大于等于距离平均值，则记为1，否则记为0；接着统计每个格网内0和1的数量，若1的数量多于0的数量，则该格网用1表示，否则用0表示；最后将生成的二值特征序列与置乱后的水印图像进行逻辑异或运算，从而构造出零水印图像。零水印构造流程如图1所示。

图1 零水印构造流程

1.1 格网划分

为更好地提取矢量地理空间数据的特征信息，反应矢量数据的局部特征，采用格网划分的方法将顶点划分成多个格网单元。读取矢量数据，得到所有坐标点的最大值与最小值，即Xmin，Ymin，Xmax，Ymax,用得到的最大值点和最小值点的横坐标和纵坐标构成矢量数据的最小外接矩形(Minimum Bounding Rectangle, MBR),最小外接矩形具有一定的稳定性，一般很少受到攻击。以数据的MBR为划分格网的基础，将MBR划分成大小相同的格网，格网划分的大小与水印图像的大小相同。划分方法如图2所示。

图2 格网划分示意图

1.2 特征序列生成

本算法以格网为单元，每一个格网内的点可表示为

vi=(xi,yi)，i=1,2,…,n.

(1)

其中:vi表示每一个坐标点，(xi,yi)表示点的坐标值，n表示顶点的个数。

1.2.1 算数平均值中心

空间分布是从总体的、全局的角度来描述空间变量和空间物体的特性[9]。其中矢量数据的分布中心是一个重要的参数，算数平均值中心是分布中心的一种，可以概略地表示分布总体的位置，其没有考虑数据之间的差异，所得的平均中心具有随机性。由于矢量数据并不总是规则分布的，随机分布的状态更为常见，计算矢量数据平均中心时会出现某些格网内没有坐标点，需要跳过该网格，不计算该格网内的算数平均值中心。

当n≥1时计算该格网内点的平均值中心[9]，记为O，计算公式为

(2)

其中:Ox，Oy分别为单元格顶点平均中心的坐标，Xi,Yi表示第i个点的X,Y坐标，n表示格网内的点数。

1.2.2 距离计算

计算每个格网内的顶点到O点的距离di，计算出di的平均值D。其中di和D的计算公式为

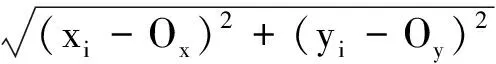
(3)

(4)

其中，n表示每个格网内的顶点个数。

1.2.3 特征矩阵生成

利用矢量数据中每个点到格网内顶点的算数平均值中心的距离来构造特征矩阵。通过比较di和D的大小生成二值序列,当di≥D时，M记为1；当di

(5)

其中，M表示二值序列。

然后将得到的二值序列压缩为64×64的二值矩阵，其大小与水印图像大小相同。压缩策略为统计每个格网内0和1的数量，若格网内1的个数大于0的个数，该格网的值为1，反之为0。

1.2.4 零水印图像构造

零水印图像的详细构造过程描述如下：

首先将原始水印图像进行Logistic置乱，以提高水印的安全性和保密性。算法中采用的水印图像大小为64×64像素，原始水印图像及置乱后的水印图像如图3所示。

图3 水印图像

然后，将得到的二值矩阵M与置乱变换后的水印图像二值序列W进行逻辑异或运算，得到零水印图像矩阵W′,即

W′=M⊕W.

(6)

其中：M表示最终的二值矩阵，⊕表示按位异或运算，W′表示置乱后的水印图像矩阵。

2 零水印的检测

零水印的检测是构造过程的逆，具体过程描述如下：

1)对待测数据进行格网划分，格网大小与水印图像大小相同。

2)计算每个格网内坐标点的算数平均值中心，并计算每个点到该平均中心的距离。

3)计算每个格网内距离的平均值，并将每个点到其相应的平均中心的距离与格网内所有坐标点对应的距离平均值进行比较，并统计大于等于距离平均值的坐标点数量和小于平均值的点数，若大于距离平均值的坐标点数占优势，则该格网用1表示，否则为0，从而生成一个64×64的二值矩阵。

4)将零水印图像与由待检测数据生成的二值矩阵进行逻辑异或运算，得到置乱的水印信息，然后将其进行Logistic反置乱变换，得到最终的水印信息。

3 实验分析

以MATLAB R2015a为平台对零水印算法进行实验，实验数据分别采用雅砻江南部地区水文测站矢量点数据、河网支流矢量线数据和湖泊矢量面数据，叠加显示效果如图4(a)所示，其中点、线、面要素分别为382 0个、963个和414个，数据格式为ArcGIS的Shp格式，将其分别划分成64×64固定大小的格网。实验中用的水印为64×64像素的二值水印图像如图4(b)所示。点、线、面数据构造的零水印图像如图4(c)所示。

图4 零水印构造实验结果

3.1 鲁棒性实验

一个好的水印算法应当在数据经过一些改变后，水印仍具有较好的可检测性。本文采用归一化相关系数(Normalized Correlation Coefficient, NC)作为评价指标，对本算法进行随机删点、格式转换、缩放和平移等攻击，以验证该算法的鲁棒性。NC[12]计算公式为

(7)

测试结果如表1所示,对点、线、面数据进行随机删点、平移、缩放、格式转换攻击后，本算法仍能较好地提取水印信息，检测到的水印图像与版权标识图像的相似度较高。但由于算法是基于格网划分构造水印的，因此无法抵抗旋转攻击。

3.2 抗裁剪攻击实验

在研究和实际应用操作中通常要对数据进行裁剪，以获得研究区的数据，裁剪操作通常较为频繁，但这却会造成水印信息的提取异常。为此，水印算法须有能力抵抗一定的裁剪攻击，从而满足实际需要，增强算法的实用性。

图5 裁剪攻击实验结果

实验通过模拟研究中的裁剪操作，对研究区内的某一岛内数据按要素进行裁剪，以获得符合要求的数据。研究区原始数据及岛要素叠加显示效果如图5(a)所示，对原始矢量点、线、面数据用岛要素进行裁剪，裁剪后数据叠加效果如图5(b)所示。然后利用裁剪后剩余数据检测零水印，以测验算法对裁剪攻击的鲁棒性。裁剪攻击后提取到的点、线、面数据的水印信息如图5(c)所示，实验提取到的点、线、面数据的水印图像与版权标识图像的相似度分别为：0.888 2，0.994 9，0.995 1。

由实验可知，本算法对裁剪攻击具有鲁棒性，但因实验中矢量点数据数据量较小，因此，抗裁剪攻击实验时实验效果不如线、面矢量数据，但检测到的水印信息与版权标识水印图像相似度仍高于88%，所以算法对数据量较小的矢量地理数据版权保护同样具有较好的适用性。

4 结束语

本文提出了一种针对矢量数据的零水印算法，通过格网划分并计算每个点到相应格网内顶点的算数平均值中心的距离和格网内的距离平均值进行比较，将矢量数据映射为和水印大小相同的二值序列，再通过与置乱后的水印图像进行逻辑异或来构造零水印图像。将零水印图像送交第三方版权认证机构进行保管，当发生版权争议时，通过算法恢复版权标识，达到版权保护的目的。实验验证算法对常见攻击具有较好的鲁棒性，能够同时适用于矢量点、线、面数据，当数据量较小时，水印检测效果也比较理想。很少很少有水印算法能抵御所有攻击，同样由于本文算法是基于格网划分的,所以不能抵抗旋转攻击,这是本文算法的不足之处，将在今后的研究中着力解决。

目前，同时适用于矢量点、线、面数据的水印算法鲜有见到，同时利用矢量点、线、面3种数据特征来共同构造水印信息的相关算法还较少，这将是今后的研究重点。

[1] 李安波,闾国年,周卫.GIS矢量数字产品版权认证技术[M].北京: 科学出版社,2012: 1-5.

[2] YAN Haowen,LI Jonathan,WEN Hong.A key points-based blind watermarking approach for vector geo-spatial data[J].Computers,Environment and Urban Systems.2011,35(6): 485-492.

[3] 朱长青,许徳合,任娜,等.地理空间数据数字水印理论与方法[M].北京：科学出版社,2014 :1-10.

[4] 许德合,朱长青,王奇胜.利用QIM的DFT矢量空间数据盲水印模型[J].武汉大学学报(信息科学版),2010,35(9): 1100-1103.

[5] 马桃林,顾翀,张良培.基于二维矢量数字地图的水印算法研究[J].武汉大学学报(信息科学版),2006,31(9): 792-794.

[6] 闵连权.一种稳健的矢量地图数据的数字水印[J].测绘学报,2008,37(2): 262-267.

[7] 王奇胜,朱长青,许德合.利用DFT相位的矢量地理空间数据水印方法[J].武汉大学学报(信息科学版),2011,36(5): 523-526.

[8] WEN Quan,SUN Tan Feng,WANG Shu Xun.Concept and application of zero-watermark[J].Acta Electronica Sinica,2003,31( 2) : 214-216.

[9] 孙鸿睿,朱建军,尹鹏程,等.一种基于矢量地图特征点和分块的零水印算法[J].地理与地理信息科学,2012,28(4): 111-112.

[10] 张佐理,孙树森,汪亚明,等.二维矢量数字地图的零水印算法[J].计算机工程与设计,2009,30(6): 1473-1475.

[11] 曹刘娟,门朝光,孙建国.二维矢量地图双重零水印算法[J].哈尔滨工程大学学报,2011,32(3): 340-344.

[12] 孙鸿睿,朱建军,李光强,等.一种基于矢量地图要素编码的零水印算法[J].工程勘察,2012,40(9): 54-57.

[13] 郭仁忠.空间分析[M].2版.北京: 高等教育出版社,2001: 77-92.

[责任编辑：刘文霞]

A zero-watermark algorithm for vector data based on distribution center

LYU Wenqing1,2, ZHANG Liming1,2

(1.School of Geomatics, Lanzhou Jiaotong University, Lanzhou 730070, China; 2. Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, Lanzhou 730070, China)

Few zero-watermark algorithm can be applied to all type vector data for copyright protection. This paper proposes a zero-watermark algorithm for vector data based on distribution center. Firstly, the vector data is divided into grid. Secondly, the distance of each point to the arithmetic mean center in the grid is calculated and distance sequence is compared with the average distance. If the distance is greater than or equal to the average, the record is 1, otherwise 0. Then, the majority of the 0 and 1 is counted in the grid and 0 or 1 is recorded to generate characteristic of data. Finally, the XOR operation is done between the shuffled watermark image and the characteristic value, then the zero-watermark image is obtained. Experiments show that the algorithm can be applied to all type vector data, and also has good robustness to common attacks including translation, scaling, cropping, format transformation, random delete point and so on.

vector spatial data; arithmetic mean center; zero-watermark; robustness

2016-09-26

国家自然基金资助项目(71563025)；甘肃省自然科学基金资助项目(148RJZA041，148RJZA028)

吕文清(1992-)，男，硕士研究生.

著录：吕文清，张黎明.一种基于分布中心的矢量数据零水印算法[J].测绘工程，2017，26(8)：50-53，61.

10.19349/j.cnki.issn1006-7949.2017.08.011

P208

A

1006-7949(2017)08-0050-04