基于CDT骨架线的地图目标邻近冲突识别

刘远刚，郭庆胜，蔡永香，柯西林 ，龙颖波，李绅弘

(1. 长江大学 地球科学学院，湖北 武汉 430100；2. 武汉大学 资源与环境科学学院，湖北 武汉 430079；3. 地理信息工程国家重点实验室，陕西 西安 710054)

基于CDT骨架线的地图目标邻近冲突识别

刘远刚1，郭庆胜2，蔡永香1，柯西林3，龙颖波1，李绅弘1

(1. 长江大学 地球科学学院，湖北 武汉 430100；2. 武汉大学 资源与环境科学学院，湖北 武汉 430079；3. 地理信息工程国家重点实验室，陕西 西安 710054)

制图综合过程中随着比例尺的缩小，不可避免地产生邻近冲突。为了在数字环境下自动地解决这类冲突，首先需要实现这些冲突的自动识别。文中提出一种基于CDT骨架线的地图目标邻近冲突识别方法。该方法首先基于CDT提取地图目标之间空白区域的骨架线；然后沿着每一条骨架线弧段所穿过的三角形路径搜索相邻地图目标之间的冲突区域(宽度小于阈值的三角形集合)；最后，从冲突涉及的地图目标、发生冲突的空间位置以及冲突严重程度3个方面给出所识别冲突的定量化描述，从而为邻近冲突的解决提供依据。

制图综合；邻近冲突；冲突识别；CDT骨架线

制图综合过程中随着比例尺的缩小，地图上的空白区域越来越小，同时为了表达的清晰性，部分地图目标不得不采用夸大的地图符号表示，导致地图上邻近目标之间的占位竞争越来越激烈，最终不可避免地产生邻近冲突。此时，一般采用移位操作对这些冲突加以处理。为了实现数字地图中移位操作的自动化，首先得实现这种邻近冲突的自动识别，首先需要知道：谁和谁冲突；冲突在什么位置发生；冲突的严重程度如何。目前，针对移位问题提出了不少邻近冲突识别的方法，主要有基于缓冲区的方法[1-4]、基于聚类分析的方法[5-6]、基于栅格数据结构的方法[7-8]和基于CDT(constrained Delaunay triangulation)或Voronoi图的方法[9-10]等。借助CDT在空间邻近表达上的优势，能够方便地在矢量地图模型下描述目标间的邻近关系,从而快速地探测地图上的邻近冲突[11]。因此，本文专注于基于CDT骨架线的地图目标邻近冲突识别方法研究，给出定量化的冲突识别和描述手段，试图为数字环境下地图目标移位操作的自动化提供支撑。

1 地图目标的Voronoi图和CDT骨架线

邻近冲突是相邻目标的邻近关系遭到破坏的结果，因此首先需要刻画出地图目标的邻近关系。一般的地图或GIS数据模型中，这种空间关系信息是无法直接得到的，需要通过专门的空间关系计算模型才能得出[12]。在计算几何领域，Voronoi图一直是用于描述和分析空间平面点集邻近关系最为有效的几何结构之一。而在地图中，空间目标按照几何图形特征可分为点、线、面3种，经典的Voronoi图不足以描述地图平面上空间目标之间的邻近关系。于是需要构造地图平面中针对点、线、面目标的Voronoi图来描述地图空间目标(群)的邻近关系。目前，对于地图目标群的Voronoi图的构造一般采用基于栅格的算法[13-15]，虽然这些算法的结果能够较准确地获取地图目标之间的中轴，避免产生过多“毛刺”，但需要事先对图形数据进行繁琐的矢栅转换和二值化等处理，增加了计算量[12,16]。而基于矢量的方法对点状目标具有较好的适用性，对于包含面状和线状等复杂几何对象的Voronoi图较难实现[17]。本文的目的是通过Voronoi图空间等距离剖分的特性表达地图目标之间的邻近关系，对生成Voronoi图的精度并无很高的要求，因此将采用基于CDT的算法构造一种矢量数据的近似Voronoi图，该结构中的每一条边是从CDT中提取出的一种相邻地图目标之间空白区域的中轴线，一般称为CDT骨架线[10,18-19]。采用文献[19]中实现的算法，提取地图目标群间的骨架线，用于本文的邻近冲突识别。如图1所示，是对百度地图上部分街区数字化后得到的实验数据，图中描述了所提取的地图上的独立地物点、建筑物和街道三类不同要素的地图目标之间的骨架线，并构建了这些地图目标之间的邻近图。每个地图目标周围由数条骨架线弧段环绕，构成一个闭合区域，该区域表达了对应目标的空间势力范围，总体上形成一种类似Voronoi图的剖分结构。图中每条弧段对应相邻两个目标之间的1阶邻近关系[20]。基于这种骨架线结构可以很容易地计算出1阶邻近目标之间的最小距离，从而为目标间冲突的探测提供定量化指标。

2 基于骨架线的邻近冲突识别与描述

借助CDT骨架线提供的邻近关系信息可以快速地识别地图中相邻两目标之间的冲突，并对冲突进行描述。具体地，可以解答以下三个问题：谁和谁冲突？冲突在什么位置发生？冲突的严重程度如何？

在CDT中，地图上相邻地图目标的空白区域被划分为多个不规则的三角形单元，所提取的骨架线结构将这些三角形串联为连通的三角形路径。沿着一条给定的骨架线弧段，依次计算其所穿过的每一个三角形在邻近地图目标之间跨过的局部最小距离，将其中小于距离阈值dmin的三角形标记出来。如果两相邻地图目标之间存在这种三角形，即说明两者存在邻近冲突；同时，这些成串标记的三角形就描绘了这两个地图目标之间的冲突区域，即确定了冲突发生的具体位置；在此基础上，进一步找出其中距离最小的三角形，从而确定两目标之间的最小距离D。该最小距离可用于说明邻近冲突的程度，即当两目标之间存在邻近冲突时，它们离得越近，说明冲突就越严重，需要移位的距离也就越大。所以本文将冲突严重程度用式(1)来定义。

sl=max[0,(dmin-D)].

(1)

式中：dmin为最小距离阈值；D为两相邻目标之间的最小距离；sl表示该冲突的严重程度。将地图符号的尺寸考虑在内，两相邻地图目标之间的最小距离阈值可以由式(2)得到。

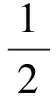
(2)

式中：dc是地图上图形之间可以辨识的最小距离阈值(一般设为0.2 mm)；r1和r2分别是两个相邻地

图目标的符号尺寸；dmin为两地图目标之间的最小距离阈值。按式(1)、式(2)计算的冲突严重程度，实际上是解决冲突时，地图目标需要移位的距离，这为进一步的解决冲突问题提供了必要信息，增强了该方法的可用性。为了统一量纲，这里用地图上通常采用的距离单位mm来度量冲突的严重程度。

以上是识别地图上不同目标之间冲突的主要思路，对于相同目标内部不同部分之间冲突的识别，思路类似，只不过所处理的骨架线弧段左右两边的地图目标是同一目标的不同部分(例如，一个弯曲的两个分支)。

为了描述和存储所识别出的冲突目标之间的冲突区域信息，定义了冲突区域对象数据结构如下(CJHJ语言描述)：

class Conflict_ Area

{

List TList;

Skeleton_ Arc ArcRef;

float Degree;

… …

}

其中TList表示该冲突区域所包含的一段连续三角形的序列，ArcRef表示该冲突区域所在的骨架线弧段的引用, Degree表示冲突的大小。每一个冲突区域对象所包含的三角形序列中至少存在一个三角形，且它们是相互连通的。也就是说，如果一条骨架线上存在多段分开的冲突三角形序列，则被分别表示为不同的冲突区域对象。这样做可以将目标之间或目标内部那些具有比较复杂的空间上下文的冲突进行分解，有助于更好地指导后续的移位操作。

如图2所示，是对与图1中相同的实验数据采用本方法进行冲突识别的结果，受篇幅所限，仅对图中的局部范围放大显示。图上三类地图要素在1∶10 000比例尺下符号化之后产生多处符号重叠和邻近冲突(符号间距不足0.2 mm)。图中各类要素对应符号尺寸分别为：独立地物点(直径3.5 mm)、建筑物面(边线宽0.35 mm)和街道线(线宽2.2 mm)。图2(b)描述了采用本文提出的冲突识别方法对实验数据进行处理得到的结果，其中所识别出的冲突区域用红色三角形表示。通过对比，可见图2(a)中所表现出的冲突及其范围和算法识别的冲突区域(图2(b))是一致的。

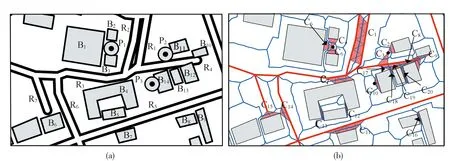
图2 基于CDT骨架线的冲突识别结果

表1中列出了图中识别出的21个冲突的详细信息，包括发生冲突的地图目标和计算出的冲突严重程度值。经对比分析可知符合图中反映的实际情况，说明本文的方法是有效的，并且该方法已经在笔者相关的移位算法研究中加以应用，这些应用也表明该方法可以成功地用于点、线、面状地图目标间的邻近冲突识别，并为移位初始向量的计算提供依据[21-23]。

需要说明的是，当两条线状目标相交时，它们之间的最小距离恒为0。采用以上方法识别出的冲突区域会包含关联线交点附近的三角形。而从视觉认知的角度看，这些区域并不属于冲突，需要排除。如图3(a)所示，可以以交点为圆心作缓冲区，与之相交的区域内，所有三角形均不作为冲突区域。其中，缓冲区的半径至少为最小距离阈值dmin，本文实验中设置为2*dmin。同理，在识别线目标内部冲突时，线目标上弯曲顶点附近三角形内部距离较小，导致弯曲左右分支之间的最小距离也小于阈值，因而被误判为线内部的冲突。为了排除这种“假冲突”情况，也需采用类似方式，此时将弯曲的顶点作为排除区域的圆心绘制缓冲区(见图3(b))。

表1 冲突信息表 mm

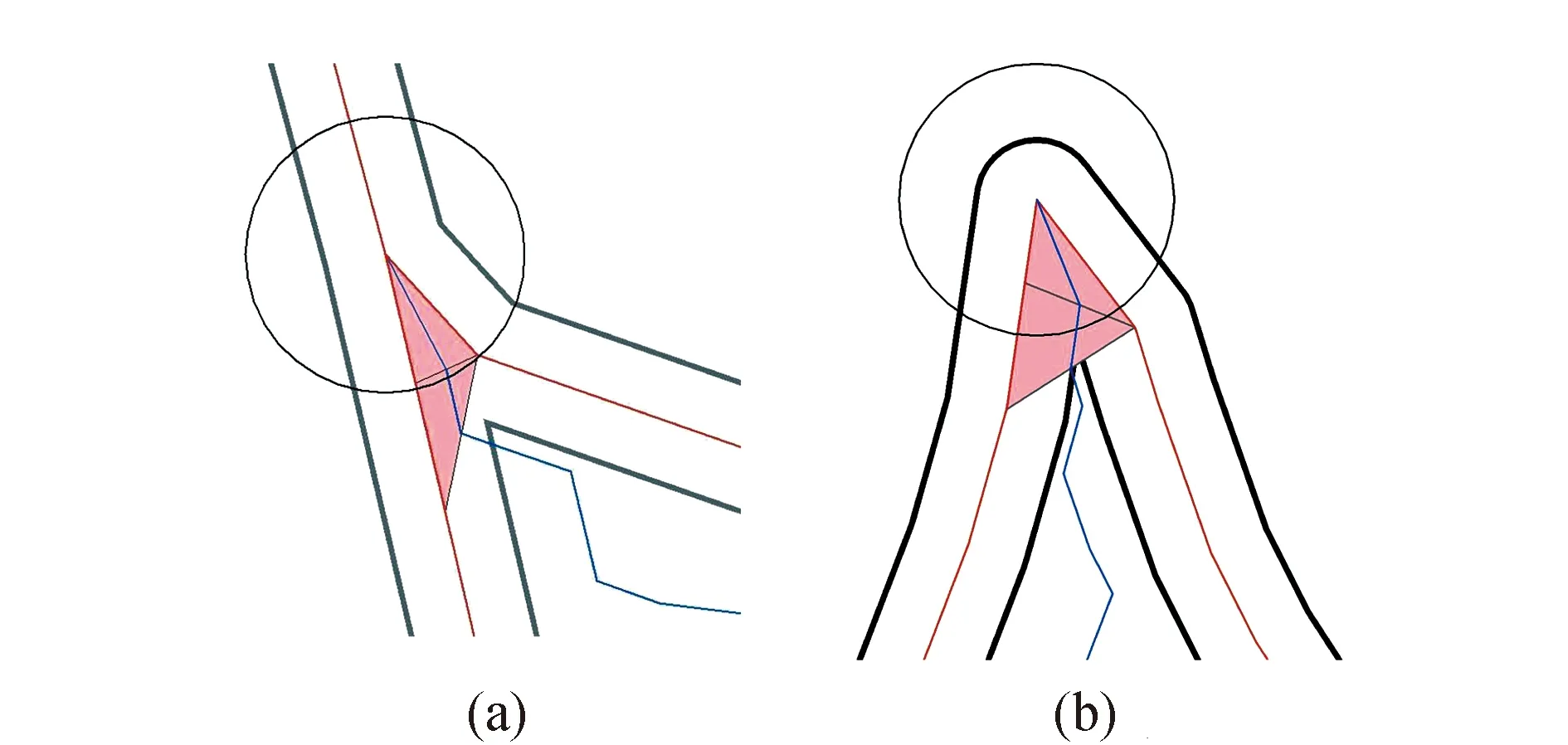
图3 排除线状目标的交点和弯曲顶点附近的“假冲突”

3 结束语

本文针对制图综合中移位操作的需要，提出了一种基于CDT骨架线的地图目标邻近冲突识别方法。该方法利用CDT骨架线所蕴含的空间邻近关系，识别相邻地图目标之间的邻近冲突，并给出邻近冲突的发生位置和严重程度的定量化描述。对实验数据的测试结果以及笔者之前有关移位算法研究中的应用情况，均表明该方法是有效的。下一步将结合制图知识和规则进一步研究所识别邻近冲突的特征和类型，为设计更合理的自动化移位操作方法提供支持。

[1] NICKERSON B G. Automated cartographic generalization for linear features [J]. Cartographica: the International Journal for Geographic information and Geovisualization, 1988, 25(3): 15-66.

[2] LONERGAN M, JONES C B. An iterative displacement method for conflict resolution in map generalization [J]. Algorithmica, 2001, 30(2): 287-301.

[3] BADER M. Energy minimization methods for feature displacement in map generalization [D]: [Ph.D.]. Switzerland: Doctorate thesis, Geographic Information System Division, Department of Geography, University of Zurich, 2001.

[4] 郭庆胜，王琳，孙雅庚，等.线图形简化与移位算子的协同方法[J].测绘学报，2016,45(7)：850-857.

[5] MACKANESS W A. An algorithm for conflict identication and feature displacement in automated map generalization[J]. Cartography and Geographic Information Systems, 1994, 21(4) :219-232.

[6] 刘晴，郭庆胜，龙毅. 比例射线移位算法的改进及其应用[J]. 测绘工程，2015，25(12)：68-71.

[8] 费立凡，何津． 解决街道与建筑物图形冲突的移位模型研究[J]. 武汉大学学报(信息科学版)，2007, 32(6): 540-543.

[9] THOM S. Automatic resolution of road network conflicts using displacement algorithms orchestrated by geographical agents [A]. In: 10th ICA Workshop on Generalisation and Multiple Representation[C]. Moscow, 2007.

[10] AI T H, ZHANG X, ZHOU Q, et al. A vector field model to handle the displacement of multiple conflicts in building generalization [J]. International Journal of Geographical Information Science, 2015, 29(8), 1310-1331.

[11] 艾廷华. Delaunay三角网支持下的空间场表达[J]. 测绘学报, 2006, 35(1): 71-76.

[12] 赵仁亮.基于Voronoi图的GIS空间关系计算[M].北京：测绘科学出版社, 2006.

[13] 刘小凤，吴艳兰，胡海. 面状要素的多层次骨架线提取[J]. 测绘学报，2003，42(4): 588-594.

[14] 胡鹏，王海军，邵春丽，等. 论多边形中轴问题和算法[J]．武汉大学学报(信息科学版)，2005，30(10): 853-857.

[15] 郭邦梅，王涛，赵荣，等. 面状要素骨架线提取算法的研究[J]. 测绘通报，2013(4): 17-19.

[16] 陈军，赵仁亮. GIS空间关系的基本问题与研究进展[J].测绘学报,1999,28(2):95-102.

[17] 乔庆华. 计算几何基础库的建立及其在地图自动综合中的若干应用[D]. 武汉：武汉大学, 2004.

[18] AI Tinghua, ZHANG Xiang. The aggregation of urban building clusters based on the skeleton partitioning of gap space [A]. The European Information Society, Lecture Notes in Geoinformation and Cartography [C]. Berlin : Springer-Verlag, 2007, 153-157.

[19] 刘远刚，郭庆胜，孙雅庚，等. 地图目标群间骨架线提取的算法研究[J]. 武汉大学学报(信息科学版) ,2015,40(2):264-268.

[20] 杜晓初，郭庆胜.基于Delaunay 三角网的空间邻近关系推理[J].测绘科学，2004，29 (6):65-67.

[21] LIU Y G, GUO Q S, SUN Y G. A complete solution of cartographic displacement based on elastic beams model and Delaunay triangulation[A]. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2014, XL-4: 163-168.

[22] LIU Y G, GUO Q S, SUN Y G,et al. A combined approach to cartographic displacement for buildings based on skeleton and improved elastic beam algorithm[A]. PLoS ONE, 2014, 9(12): e113953.

[23] 刘远刚，郭庆胜， 孙雅庚，等. 地图自动综合中Beams移位算法的实现与改进[J]. 武汉大学学报(信息科学版)，2016, 41(4): 450-454.

[责任编辑：张德福]

Identifying proximity conflicts of map objects based on CDT skeleton

LIU Yuangang1, GUO Qingsheng2, CAI Yongxiang1, KE Xilin3, LONG Yingbo1, LI Shenhong1

(1. School of Geoscience, Yangtze University, Wuhan 430100, China; 2. School of Resource and Environment Science, Wuhan University, Wuhan 430079, China; 3. State Key Laboratory of Geo-information Engineering, Xi’an 710054, China)

In the process of cartographic generalization, duo to the reduction of scales, it is inevitable to encounter proximity conflicts. In order to solve these conflicts automatically in the digital environment, it needs to realize the automatic identification of the conflicts at first. This paper proposeds a method to identify the conflicts on the basis of constrained Delaunay triangulation skeleton. Firstly, the skeleton of white space between neighboring map objects are extracted. Then, the conflict regions between neighboring map objects are identified by using triangular path along each skeleton arc. It is represented by triangular sets with a width less than a threshold. Finally, the quantitative description of the identified conflicts from three aspects is given, including the conflicting map objects, the spatial location of conflict and the degree of conflict, which can provide the basis for the solution of proximity conflicts.

cartographic generalization; proximity conflicts; identification of the conflicts; CDT skeleton

2016-01-19；

2017-3-4

国家自然科学基金面上项目(41471384)；湖北省教育厅科学研究计划指导性项目(B2015448)；地理信息工程国家重点实验室开放基金课题资助(SKLGIE2016-Z-4-1)；长江大学大学生创新创业训练计划项目(2016010)

刘远刚(1982-)，男，讲师，博士.

郭庆胜(1965-)，男，教授，博士生导师.

著录：刘远刚，郭庆胜，蔡永香，等.基于CDT骨架线的地图目标邻近冲突识别[J].测绘工程，2017，26(8)：10-13，19.

10.19349/j.cnki.issn1006-7949.2017.08.003

P208

A

1006-7949(2017)08-0010-04