伺服控制系统的复合模糊自适应PID控制*
余容,孙浩然,何朝明(西南交通大学机械工程学院,成都610031)
伺服控制系统的复合模糊自适应PID控制*
余容,孙浩然,何朝明
(西南交通大学机械工程学院,成都610031)
以工程中的伺服控制系统为研究对象,提出一种嵌入比例因子的复合模糊自适应PID控制方法,即将比例因子模糊控制与模糊PID控制结合而成的复合模糊控制。首先通过MATLAB/Simulink系统工具对无干扰理想状况下的系统进行仿真与分析,然后进一步模拟真实环境下的系统运行状况,在某一时刻加入干扰信号,并将比例因子模糊控制嵌入模糊PID控制中优化算法,对控制系统不断加以改善与优化。试验结果表明,此方法比传统PID控制更具优势,能有效改善控制系统的响应时间、调节时间以及抗干扰能力,有效提高控制系统的动态性能和鲁棒性。
伺服控制系统;传统PID控制;模糊自适应PID;比例因子
0 引言
当前智能控制算法的伺服控制系统应用较为广泛,对系统实时性、稳定性、抗干扰能力等方面要求较高。伺服控制系统具有非线性及未知性,系统运转过程中常会遇到未知的突发状况等干扰,需及时进行自我调节并能在有效范围内快速恢复平稳状态。陈智勇[1]等采用电流、位置、速度三闭环的控制方式与电压矢量调制控制算法实现伺服控制;武星[2]等采用多目标遗传算法优化伺服控制器的PID参数方法实现伺服控制;S.Kissling[3]采用迭代反馈整定的方式实现对伺服系统的控制参数进行整定。综合国内外相关伺服控制算法,各有利弊,应结合实验背景及应用领域对控制算法进行研究。文章提出一种嵌入比例因子的复合模糊自适应PID控制方法,在广泛应用的模糊PID控制算法中嵌入比例因子进行复合模糊控制。简单PID仅限于数学模型精确的控制系统[4-5],而模糊PID控制算法有适应非线性和时变性等优点,其抗干扰能力强、动态性能好,且无需精确数学模型[6-7]。控制系统将模糊自适应PID控制与PLC结合,采用模糊自适应PID控制算法对参数自调整,通过PLC实现模糊自适应控制策略,可提升伺服控制系统的响应时间、控制精度和平稳性。
1 伺服自适应控制系统模型
1.1 模糊自适应PID控制算法
传统PID算法单一,复杂工况下无法对参数进行实时自整定。尤其应用在特殊环境下的伺服控制系统,例如转运核废料的智能起重机,在扰动环境下,系统实时性与鲁棒性较差[8]。对模糊自适应PID控制系统而言,需找出PID的系统参数kp、ki、kd与偏差e、偏差变化率ec间的模糊关系,通过不断检测e和ec的方式,基于模糊控制原理对3个控制参数调整,使伺服系统具有良好的动静态性能[9],其系统结构见图1。

图1 模糊自适应PID伺服控制系统框图
以误差e和误差变化率ec作为输入,模糊控制自整定参数ΔKp、ΔKi及ΔKd作为输出,将输入输出的模糊论域均设定为{-3,-2,-1,0,1,2,3},则对应的模糊子集为{NB,NM,NS,Z,PS,PM,PB},并且采用对称分布的三角形隶属函数。模糊控制规则是模糊控制器设计的核心,模糊控制规则采用如下格式:
if E is A and EC is B,then U is C
PID参数自调整规则可总结为表1~表3。

表1 ΔKp模糊规则表

表2 ΔKi模糊规则表

表3 ΔKd模糊规则表
在工业控制中常采用质心法(centroid)进行去模糊化,即:

其中,u(xi)为隶属函数,论域上元素xi为隶属函数u(xi)的加权系数;xavr为加权平均后的平均值。
1.2 系统模型设计
以伺服控制系统为对象,采用模糊自适应PID控制算法,通过PLC实现对伺服电机的控制。伺服电机分为转矩控制、位置控制和速度控制等模式,考虑各方式特性,结合系统的功能需求,选取合适的控制模式。基于位置控制模式,通过PLC输出对应的脉冲信号到伺服驱动器,需设置相应的增益参数对数据进行关系转换。
基于图1伺服控制系统框图,建立如图2所示的系统仿真模型,并将传统PID控制与模糊自适应PID控制并行试验,分别对系统的响应特性、超调量、调节时间、平稳性等方面进行比较分析。比例系数可加快系统的响应速度,减小系统稳态误差;积分系数可消除系统的稳态误差,但太大会在响应过程的初期产生积分饱和;微分系数可改善系统的动态特性,若过大则会延长调节时间,从而降低系统的抗干扰性。总结对应的特性与优劣,并依据试验结果,结合工程中实际运用条件,对系统不断进行优化改善,使此控制系统达到较为良好的控制效果。

图2 系统初步仿真模型图
建立系统模型,并对其进行仿真实验,仿真过程中需要对各环节的增益、常数修正值等系统参数进行对应调整,其中PID的主要参数kp、ki和kd对系统平稳性、稳态精度和超调量等控制性能指标均有重要影响。从系统的动静态综合性能角度考虑,在不同的误差e和误差变化率ec状况下,控制过程对参数自整定也会有不同的要求,常常参考实际工程经验总结出的参数自整定原则,并结合误差e和误差变化率ec,可根据系统的响应速度、震荡程度、趋于稳定的时间长短等等实际运行状况,进行参数自整定调整[10]。参数自整定的取值较大较小是针对对应参数初始值而言,在实际应用中PID参数是基于其初值而自调整得出,即:

其中,kp0、ki0、kd0分别为P、I、D参数的初始值,Δkp、Δki、Δkd分别为依据系统实际运行中的e和ec由模糊推理得出的自调整量。
1.3 系统模型优化
根据建立的系统仿真模型试验,经过不断的调试使控制系统的响应速度、超调量、稳定性等指标逐渐达标,可达到较好的控制效果。但是在实际工程运用中,系统时常会出现不定时干扰或负载发生变化等未知状况,因此需要对系统进一步优化与改善。
广泛应用于工业领域的伺服控制系统应具有高精度与良好的实时性,则需要将控制率的计算量尽可能减小,并在一定条件下,对外界未知扰动应满足较好的鲁棒性。因此,通过嵌入比例因子的模糊控制,在线修正比例、微分环节,对系统进一步进行优化。在未知扰动、负载发生变化或启动误差较大时,会使误差e发生一定的跳变,嵌入比例因子的模糊控制环节进行自我调节,使系统快速响应并跟踪其参考信号,从而改善系统的鲁棒性与动态性能。在运行各阶段,系统对比例因子的需求并不相同,根据系统的运行状况对控制量在线整定,可大大改善系统的控制效果[11],比例因子a、b的模糊控制规则见表4。

表4 比例因子a、b的模糊规则表
2 仿真与分析
2.1 理想型模糊自适应PID控制
选取伺服系统的数学参考模型[12]为:
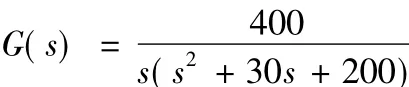
模拟仿真时,控制系统在无扰动环境下,选取仿真时长t=100s,对控制系统以传统PID控制与模糊自适应PID控制两种控制方式进行并行试验,分别对其进行比较、分析以及调试,使运行结果达到较为满意的效果,系统运行曲线如图3所示,其局部放大示意图见图4。

图3 理想型系统运行曲线图

图4 理想型系统运行曲线局部放大示意图
从上图系统运行曲线可知,两种PID控制方式下系统性能都较好,二者均能快速趋于平稳,减少对应的调节时间。虽然传统PID控制比模糊自适应PID控制平稳且没有超调量,但是模糊自适应PID控制在具有更快的响应速度下也能快速趋于平稳,若在系统运行可靠环境下更能提高系统工作效率。
2.2 优化型复合模糊自适应PID控制
在实际环境下,难以避免出现负载变化等扰动现象。因此,模拟真实环境下,考虑干扰因素,在某一时刻对系统加入干扰信号,并对模糊自适应PID控制与比例因子结合进行复合模糊控制。

图5 优化型系统运行曲线图
选取仿真时间t=100 s,对系统分别采用传统PID控制与模糊自适应PID复合控制进行试验,系统运行曲线图如图5所示。根据图5系统运行曲线,传统PID控制下系统的响应速度较慢,会产生较大超调量,在一段时间内震荡剧烈,系统反应速度较慢,且调节时间更久,系统的鲁棒性较差。在t=20 s时加入扰动,虽在短时间内模糊自适应控制下系统也会产生较小的超调量,但系统响应较快,能快速检测到干扰并能及时进行自我调整,几乎能在2s内快速趋于平稳,且没有过于明显的震荡,能有效提高系统的动态性能,使系统的控制效果更佳,其局部示意图见图6、图7。

图6 快速响应局部示意图

图7 抗干扰局部示意图
3 总结
模糊自适应PID复合控制方法对于受控系统一方面无需具备准确的数学模型,另一方面也可对参数进行自调整。文章在MATLAB/Simulink系统工具下,基于模糊PID控制算法,并且分别在传统PID控制、模糊PID控制以及改进后的复合模糊自适应控制环境下,对自适应伺服系统进行模拟试验、分析与优化。试验结果表明,模糊自适应PID控制算法具有良好的控制效果,能有效改善系统的响应速度,缩短调节时间以及增强系统的抗干扰能力,可有效改善系统的动态性能和鲁棒性。此外,在工程应用中亦可提高自适应控制系统的可行性,使控制系统更具智能化,具有重要的应用价值。
[1]陈智勇.基于浮点DSP TMS320F28335的交流伺服控制系统研究[D].杭州:浙江大学,2011.
[2]武星,楼佩煌,唐敦兵.自动导引车路径跟踪和伺服控制的混合运动控制[J].机械工程学报,2011,47(3): 43-48.
[3]S.Kissling,Ph.Blanc,P.Myszkorowski,et.al.Application of iterative feedback tuning(IFT)to speed and position control of a servo drive[J].Control Engineering Practice,2009,17 (7):834-840.
[4]纪志成,沈艳霞,薛花.无刷直流电机自适应模糊控制的研究[J].中国电机工程学报,2005,25(5):104-109.
[5]赵志勇,于东,王志成,等.伺服系统速度环参数整定技术的研究[J].组合机床与自动化加工技术,2016(2): 65-69.
[6]张营,巩永光,陈立锋.交流伺服系统单神经元PID自适应预测联合控制[J].组合机床与自动化加工技术,2015(12):46-48.
[7]冯江涛,郭晓松,仕润霖,等.基于模糊PID控制的起升过程仿真研究[J].机械设计与制造,2013(6):193-196.
[8]孙春亚,吴楝华,喜冠南.电液伺服模糊PID位置控制系统设计及应用[J].机械设计与制造,2016(6):155-158.
[9]赵国山,仇性启.自适应PID的发展概况[J].化工自动化及仪表,2006,33(5):1-5.
[10]尹霞,黎亚元,万志伟.数控伺服系统模糊PID控制仿真研究[J].装备制造技术,2008(11):103-104.
[11]姬伟,李奇.陀螺稳定平台视轴稳定系统自适应模糊PID控制[J].航空学报,2007,28(1):191-195.
[12]汤红诚,李著信.Matlab在模糊PID伺服系统控制中的应用[J].仪器仪表学报,2003,24(s2):595-596.
(编辑李秀敏)
Compound Fuzzy Adaptive PID Control of Servo Control System
YU Rong,SUN Hao-ran,HE Chao-ming
(School of Mechanical Engineering,Southwest Jiaotong University,Chengdu 610031,China)
A compound fuzzy adaptive PID control method w as proposed for the servo control system in engineering.This method bounded proportionalfactor fuzzy controland fuzzy PID control.Firstly,the analog simulation and analysis was taken for the idealsystem with no interference through the MATLAB/Simulink.Then the simulation w as taken w ith interference signal at a time and integrating the proportional factor and fuzzy PID control,to imitate the real situation of system operation and continue to improve the control system.The experiment show s that this method possesses more advantages compared with traditional PID.It can effectively ameliorate the response time,adjustment time,anti-interference ability,improve the dynamic performance and robustness of the control system.
servo control system;traditional PID control;fuzzy adaptive PID control;proportional factor
TH166;TG506
A
1001-2265(2017)04-0075-03
10.13462/j.cnki.mmtamt.2017.04.018
2016-08-21;
2016-09-05
国家自然科学基金(51275431);四川省科技攻关计划(2014GZX0009)
余容(1991—),女,重庆丰都县人,西南交通大学硕士研究生,研究方向为智能控制、CAD/CAM,(E-mail)yurong9966@hotmail.com;
何朝明(1972—),男,成都人,西南交通大学副教授,博士,研究方向为智能控制、CAD/CAM,(E-mail)fly2005@126.com。

