Measurement ofthe spatialspeci fic impulse distribution due to buried high explosive charge detonation

V.Denefeld,N.Heider,A.Holzwrth

aFraunhofer Institute for High-Speed Dynamics,Ernst-Mach-Institut,EMI,Eckerstraße 4,79104 Freiburg,Germany

bErnst-Mach-Institut,Am Christianswuhr 2,79400 Kandern,Germany

Measurement ofthe spatialspeci fic impulse distribution due to buried high explosive charge detonation

V.Denefelda,*,N.Heidera,A.Holzwarthb

aFraunhofer Institute for High-Speed Dynamics,Ernst-Mach-Institut,EMI,Eckerstraße 4,79104 Freiburg,Germany

bErnst-Mach-Institut,Am Christianswuhr 2,79400 Kandern,Germany

A R T I C L E I N F O

Article history:

Buried high explosive

IED

Momentum transfer

Speci fic impulse

Local momentum distribution

Vehicle

Detonation

Ring arrangement setup

Quartz sand

Alluvial sand

Depth of burial

Water content

Saturation

X-ray

High-speed camera

Buried high explosive(HE)charges represent a high threat to military vehicles.The detonation of these charges can lead to signi ficant momentum transfer onto vehicles and their occupants.A detailed understanding of the physical processes involved in the loading of vehicle structures is necessary for an optimization of effective countermeasures and protection systems.A quantitative description of the local momentum distribution on the vehicle underbody due to the detonation process is of special importance.In the following,a new test setup is presented that allows the experimental determination of the speci fic impulse distribution.It is based on a ring arrangement where the elements are nested into each other and the velocity of each ring is correlated with the local speci fic impulse at its position.

The momentum transfer to a vehicle depends on a number of in fluencing factors such as:charge mass, embedding material(e.g.sand,gravel,clay),density,water content,saturation,depth of burial,ground clearance and vehicle shape.The presented technology is applied to quantify the in fluence of the embedding material(alluvial sand,quartz sand),the burial depth and the water content on the local speci fic impulse distribution.The obtained data can be used as initial condition for the numerical simulation of occupant safety assessment and as input for empirical modeling of momentum transfer on structures.

©2017 The Authors.Published by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

1.Introduction

Military operations during the last two decades were characterized by asymmetric threat scenarios.Specialattention has been given to the effects ofland mines and improvised explosive devices (IEDs)on vehicles.A detailed review about anti-tank mines and their effects is given in Ref.[1].The detonation of mines or IEDs leads to a complex sequence of loading phenomena on vehicle structures.Important effects in this context are the interaction of the blast wave or detonation products with the vehicle as a whole, but also local impacts of primary or secondary fragments onto the vehicle surface.Thus,loading effects can be classi fied into localand global phenomena.Local effects are related to the impact of projectiles and the development of protective systems with threat adapted materialcombinations.This paper deals with the physical effects that are caused by the detonation of buried high explosive charges below the military vehicle.In this case,a large momentum transfer on the vehicle structure as a whole takes place and leads to high accelerations of the vehicle and the occupants.

First,most research concentrated on the analysis of low buried mines,and techniques were developed to measure momentum transfer[2,3]and the local deformation of vehicle floor structures [4,5]due to mine detonation.Simulation models for the assessment ofmine effects on vehicles were developed[6-8].Specialattention was given to modeling the charge detonation in a sand environment(with adequate material models)and the following interaction with a momentum trapping structure[9,10].It was realized that the burial conditions and the embedding material properties show a signi ficant in fluence on the momentum transfer[6,11-16].With the appearance of IEDs,phenomena in connection with deeply buried charges oflarge masses became ofinterest[17-19].It turned out and was partially unexpected that this type of threat caused a signi ficantly increased momentum transfer.Hence,there was the need for a better understanding of this loading process. In fluencing factors are:charge mass,embedding material(e.g. sand,gravel,clay),density,water content,saturation,depth of burial,ground clearance and vehicle shape,to mention only the most signi ficant parameters.In most test setups,only the global momentum transfer on a large-area structure was examined.For a better understanding of the loading process,locally resolved information about the speci fic impulse distribution on a structure is necessary[20-26].We therefore developed a new test technology based on a ring arrangement with each individual ring used as a momentum trap at the corresponding localposition.The HE charge is placed in a barrel structure and embedded within the selected material that is prepared under highly reproducible conditions. After detonation of the charge,the detonation products and the accelerated embedding material interact with the ring arrangement and transfer locally different amounts of impulse on each ring.From the different ring velocities,the corresponding impulse can be derived.For the determination of the ring velocities, redundant measurement techniques are used.In the following,the development of the test design with numerical simulations is shown.The method is used to quantify the in fluence of several burialparameters on the localmomentum distribution.Parameters varied are the embedding material,the water content and the burial depth.The detailed local momentum distribution can be used as initial conditions for numerical simulations of loading processes ofvehicles.Additionally,they provide validation material for the empirical description of momentum transfer on structures that is used in several commercial simulation tools.

2.Experimental arrangement

2.1.Description of the experimentalsetup

In order to characterize the effects ofa buried HE charge,mostof the tests presented in the literature use large area steelplates as a momentum trap.This approach delivers no information about the spatial momentum distribution.Therefore,a new experimental method has been developed by which the local distribution of the momentum transfer from a HE detonation on a vehicle structure can be obtained.The principle idea is to measure the velocity and thus the momentum transfer of different rigid bodies at different spatial positions that are exposed to the detonation of the buried HE charge.The localspeci fic impulse is determined from the mass, the gained velocity and the surface area ofthe corresponding body hit by the detonation products.The exposed surface areas of the objects determine the local resolution of the speci fic impulse measurement.

Our testtechnology is based on an arrangement with concentric rings where each individualring is used as a momentum trap atthe corresponding localposition(see Fig.1).The arrangement is placed above a sand filled barrelthatcontains the HE charge.The rings are fixed with wires at the ceiling of the experimental hall and precisely aligned with respect to the sand barrel and its surface.

The ring velocities are determined with redundant measuring techniques:X-ray diagnostic and high-speed camera.

The experimentalsetup is shown in Fig.1.The explosive charge is embedded in an accurately prepared sand environment.The sand barrel has a diameter of 63 cm and a height of 80 cm,which is replaced for each test and is filled with sand again.

2.2.Charge de finition

A PETN charge(with a density of 1.54 g/cm3)has a mass of84 g with a diameter of 59.2 mm.The depth of burial of the explosive charge(distance from the top of the charge to the top of the soil) varies from 46.4 mm to 116 mm.The initiation ofthe charge occurs at the center of the bottom of the explosive charge.The distance between the sand surface and the ring structure is 139 mm.

2.3.Sand de finition

A de fined and reproducible preparation of the embedding material is of great importance.For our tests we used loose sand material which is a heterogeneous material consisting of the quartzite grains,water and the air voids.The effects of buried HE charges depend strongly on the actualcomposition between these three components.It is therefore necessary to prepare a largely homogeneous mixture of the components within the test barrel. Specialattention was given to an exact determination of the water content and the water saturation.The intention was to determine the localmomentum distribution as a function ofthese parameters.

Two differentsand types have been chosen for the experiments: an alluvialsand,with 5%water content,and a dry quartz sand.The grain size distributions for the materials are shown in Fig.2.It can be seen that 80%of the sand particles have a size between 0.1 mm and 0.3 mm which corresponds to a rather fine-grained particle distribution.

As mentioned before,the two parameters water contentand the saturation are of specialimportance for the preparation of de fined test conditions.Both parameters have to be prepared in the sand barrel as homogeneous as possible connected with a precise experimental determination of their actual values at the time of testing.

Therefore,we determined the following parameters for each experiment:wet densityρwet,water content w,dry densityρdryand saturation S.In the following we give a short summary of the measurements and formulae used for the determination of these parameters.

Shortly before the test,the selected amount of water and sand was mixed and evenly distributed in the test barrel.Afterwards, sand samples(with mass msample)were taken from the prepared sand in the test barrel with help of a core cutter(height 120 mm, diameter 96 mm,volume Vsample=868 mm3).

The wet sand densityρwetresults from Equ.1

The taken sand sample is then heated ata temperature of105°C untilthe complete water fraction has disappeared from the sample. The sand sample is then weighed and the mass ofthe dry sand mdryis determined.

The water content w is calculated from Equ.2

with mwaterbeing the evaporated water mass.

The dry densityρdryis calculated from Equ.3

which finally gives the saturation ratio S with Equ.4

whereρsis the density of the single quartz grain which has a value ofρs=2.65 g/cm3.

3.Design of the rings

The design of ring shapes requires a detailed analysis of the expected initial velocities and trajectories of each individual ring element.This is of special importance for the X-ray and optical measurement of the ring velocities.An unambiguous allocation of the rings is only possible if overlapping of the inner rings by outer rings can be avoided.In order to ensure that the rings willbe visible on X-ray pictures,the heights of the rings have to be optimized with the help of numerical simulations.For example,if an outer ring would fly faster than the inner rings,these rings would be covered and not observable on the X-ray picture anymore.A variation ofthe geometry ofthe ring shape has been done to achieve an optimalvelocity for each ring.

To avoid contact of the flying rings with the ceiling of the experimental hall,a certain initial velocity must not be exceeded. For our test conditions the maximum flight height should be less than 3 m which corresponds to a maximum initial velocity of less than 7.7 m/s.

The selected ring con figuration is presented in Fig.3.It consists in 8 concentric rings with a thickness of 20 mm and with heights ranging from 60 mm to 140 mm.The total weight of the rings is 57 kg.Special attention has been devoted to the choice of an appropriate gap size between the rings of0.2 mm,smallenough to prevent that sand fills the gap,and large enough to minimize friction.On top ofthat,oilhas been added between the rings and it has been checked before each experimentthat the rings could slide between them.

4.Diagnostic methods

In order to calculate the speci fic impulse,an accurate measurementofthe initialring velocity is necessary.For the diagnostic, a 3-channel X-ray flash unit and a high-speed camera are used to measure the velocity ofthe rings.Fig.4 shows an overallview ofthe experimentalsetup as created at the test facility.An X-ray film anda measurementgrid for the determination ofthe ring displacement are located behind the sand barrel.A 3-channel X-ray source (multianode tube)for the production ofthe X-ray flash pictures can be seen on the right.The sand barrelis located in the center of the picture,with concentric rings for the impulse measurement.On the left,wooden blocks are placed for protection against fragments.

For the X-ray analysis,the flight height and the trigger times are determined with the numerical simulation.The velocity of the rings during their rising phase is presented in Fig.5 for a depth of burialof 46.4 mm.

Using X-ray diagnostics,two or three images are taken after the initiation of the charge.With numerical simulations,it has been showed that the impulse is completely transferred onto the rings after about 2 ms.The determination of the initial velocity of the rings should therefore start after 2 ms in order to prevent disturbing in fluences from the acceleration phase.As a consequence, the trigger time of the first X-ray picture will be set 2 ms after the initiation of the explosive.”

Initialvelocity values v0can easily be determined from the path and time differences between two X-ray pictures.An example of two X-ray pictures is given in Fig.6.If s1and s2are the positions of the rings at the corresponding recording times t1,t2,v0results from Equ.5

with g=9.81 m/s2the acceleration due to gravity.

The speci fic impulses iStransferred to the rings are then calculated using Equ.6

with m the mass of the ring and F the annular surface,[iS]=[kg/ m·s]=[Pa·s].

Another method to evaluate the initialvelocity ofthe rings is the use of the high-speed video.

The video films cover the entire flight phase of the rings over a period of 2000 ms.The detonation flash and the sand particles make the evaluation of the velocity of the rings in the first milliseconds of the video very dif ficult.The cases in which the rings are observable when they fall back to the starting position(see,for example,Fig.7)can nevertheless be used to calculate the transferred impulse from the flight time.In this case,the initialvelocity v0is given by Equ.7with the flight time tfand the gravitationalconstant g=9.81 m/s2.

A comparison of the initial velocity determined by the two methods is given for test No.2 in Table 1.The ring No.5 is not discernable on the high-speed video.

Regarding the measurement accuracy,the two experimental methods for the determination of the ring velocities are in good agreement.The evaluation of the ring velocity using X-ray diagnostics,however,proves to be more reliable and willbe preferred in the following.

5.Experimental measurement of the spatial speci fic impulse distribution

In the following,the experimentally determined spatialspeci fic impulse distributions are presented.Table 2 shows an overview of the 10 experiments including the performed variation ofthe burial conditions.Experiments 1 to 4 were carried out with alluvialsand, Experiments 6 to 10 with quartz sand.The depth of burial was chosen to be 46.4 mm and 116 mm for alluvial sand and 46.4 mm for quartz sand.The variation of water content and saturation was done for quartz sand(water content between 0 and 20%and saturation between 6%and 67%).

Experiment results showing the speci fic impulse as a function of the radial distance are shown in Fig.8 for the alluvial sand.The error bars correspond to the maximum and minimum value in the two tests with similar embedding conditions.The comparison of the results for the 2 different burial depths shows the interesting fact that the speci fic impulse distribution is more concentrated to small radial distances for the higher burial depth.Up to the radial distance of 70 mm,the test with a depth of 116 mm shows significantly higher impulse values.Going to larger radial distances (90 mm and more),the shallow buried charge causes the larger momentum transfer to the structure.The physical explanation is quite intuitive because the deeper buried charge is more contained by the surrounding material and thus the detonation products are directed more perpendicularly and concentrated with respect to the embedding material surface.It is remarkable that the total momentum transfer integrated over the complete loaded area is nearly identicalfor both burialdepths(see Fig.9,with a maximum value of 174 kg·m/s after integration over the complete loaded area).This demonstrates that the loading of a vehicle due to a buried charge detonation depends sensitively on the burial depth but also on the vehicle area that collects the ejected ground material.An exact quanti fication of the loading conditions thus requires the detailed knowledge of the spatial speci fic impulse distribution with respect to the vehicle ground floor.

The corresponding results for the quartz sand are shown in Fig.10.For this material,a systematic variation ofthe water content and saturation has been done.The corresponding results for the speci fic impulse are shown in this case as a function of the radial distance and the degree ofsaturation.Saturation values are 0%,32% and 66%.Itis found thatthe scattering ofthe experimentalresults isquite smalland thus a reproducible preparation ofthe soilhas been achieved.Surprisingly it can be observed that directly over the mine,the dry sand causes higher speci fic impulse than the wet sand.For some radialdistances up to 90 mm there is nearly a factor of 2 between dry and wet sand.For larger distances,wet sand shows signi ficantly higher speci fic impulse values.Remarkable is the fact that the experiments with water saturation of32%and 66% show nearly no difference within the experimentalerror.It is again interesting to look at the totalintegrated momentum in Fig.11,and at the summary for all sand con figurations in Fig.12.The cumulative integrated impulse as a function ofradialdistance shows again the higher values for the dry sand but with increasing radial distance,dry sand and wetsand show a converging behavior.The total momentum integrated over the complete loaded area for the dry sand(value of 242 kg·m/s)leads only to a slightly higher momentum transferofaround 14%compared with the wetsand(about 213 kg·m/s).The total momentum transfer for the 32%and 66% saturation is identical and shows no further dependence on this parameter.Our experimental results do not support a signi ficant effect of saturation in the parameter field that we investigated.

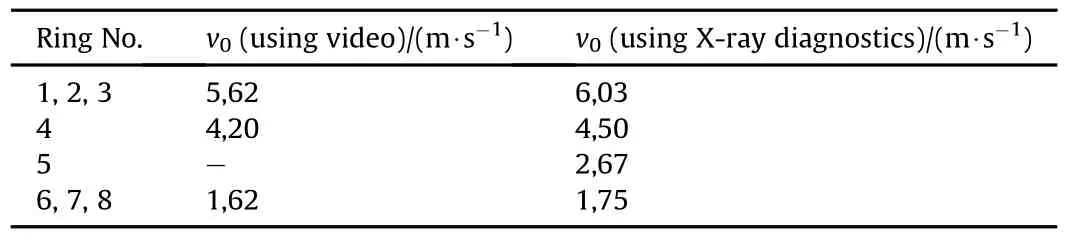
Table 1 Determination of initial velocity of the rings for test No.2.

6.Numerical simulation

6.1.Variation of the depth of burial of the charge

For a detailed analysis of the experimental results,simulation models of the test setup have been developed.The concentric ring arrangement shows rotational symmetry and therefore allows 2D as well as 3D finite element simulations.The 3D numerical simulation modelis shown in Fig.13.Simulations are executed with the finite-element software LS-DYNA.The rings are represented by a Lagrange model(32 000 solid elements),the embedding material with the HE charge and the surrounding air are represented by an Euler model(1.4 million solid elements).The detonation process is simulated with a complete Euler-Lagrange coupling method.Special attention must be addressed to the material modeling of the sand material.The modelfrom Laine and Sandvik[9]for sand was used,which includes an equation of state for the compaction of loose sand particles and a Mohr-Coulomb type model for the strength behavior.The initial density of the sand was set to 1,3 g/ cm3by scaling the equation of state of the model of Laine and Sandvik.

The depth of burial of the charge was varied from 23.2 mm to 116 mm.The speci fic impulse and the maximalvelocity ofthe rings are shown in Fig.14 and Fig.15,respectively.

The momentum transferred to the rings is concentrated within a circular area ofabout15 cm radius.The maximalvelocity ofthe ring is about 6 m/s,and the maximal flight height about 1.8 m,meeting the requirement of the testing facility.

It can be observed that the impulse is focused directly above the charge for small depths of burial.For more deeply buried charges, the impulse is transferred outwards.

6.2.Comparison with experiments and extension of the model

Special attention has been devoted to validate the material model and to increase the lateral extension of the observation range.In the experiments,the radius of the ring arrangement is 160 mm and partofejected materialand thus momentumwillpass the test setup.Numerical simulations provide the information about the momentum that is not detected in the experiment.The simulation model with an extended 600 mm momentum trap con figuration is presented in Fig.16.

The numericalsimulations are validated and compared with the experiments 3 and 4(alluvialsand,depth ofburial46.4 mm)wherethe prepared testconditions match with materialparameters ofour selected materialmodel.

Table 2 List of the experiments with prepared burial conditions.

The speci fic impulse distributions from Experiment 3 and 4 are compared with the numericalsimulation in Fig.17.The integrated cumulative momentum is shown in Fig.18.Regarding the speci fic impulse,the simulation values are ranging from 5.5 kPa·s in the center region to 1.3 kPa·s for the maximum observed radial distance.The corresponding average test values are in the range from 5.4 kPa·s for the first ring to 1.1 kPa·s for the outer ring.Regarding the cumulative impulse distribution,the average totalmomentum integrated over the complete loaded area for Tests 3 and 4 is 178 kg·m/s.The total momentum calculated with the numerical simulation is 187 kg·m/s,within 5%from the average total momentum of the experiments.Overall,a good agreement between numerical simulation and the experiments is observed.

Another method to quantify the speci fic impulse distribution is based on the work of Westine(see Refs.[27]and[28]).Westine conducted experiments with buried explosives in soil.He then used an analytical empiricalapproach to postulate a formula where the localdistribution ofthe speci fic impulse on a flat plate is given as a function of the con figuration(mass,energy and geometry of the explosive,burial depth,distance to the plate).The functional dependence of the speci fic impulse on the radial distance resembles the shape of a Gaussian bellcurve with a strong decrease with increasing radial distance to the charge center.The corresponding speci fic momentum distribution calculated from the Westine formula is compared with our experimental results and our simulation and is shown in Fig.17.It is obvious that the analyticalformula overestimates the experiments by about50%and thus can be used only for a rough estimate of buried chargedetonation effects.

The cumulative impulse distribution calculated with the additionalmomentum traps of 300 and 600 mm radius(Fig.19)shows that the cumulative impulse still increases with increasing ring radius,with values of 265 kg·m/s at a radius of 300 mm and of 310 kg·m/s at a radius of600 mm.The totalmomentum trapped by the tested con figuration(160 mm ring radius)corresponds to about 60%ofthe totalmomentum thatwould have been trapped with the 600 mm ring radius.Itcan be supposed thatfor our burialcondition and a radius of the momentum trap from 600 mm,the total momentum of the explosive charge and of the sand has been transferred.

7.Summary

A measurement technique was presented that allows the experimental determination of the localspeci fic impulse distribution ofa buried HE charge detonation.The test setup was designed and optimized with numerical simulations.An arrangement of concentric rings where the individual rings are nested into each other was found to be particularly suitable for speci fic impulse measurement.The vertical ring velocities were measured and correlated with the transmitted speci fic impulse.X-ray imaging and high-speed video recordings were used to measure the ring velocities.The different diagnostic tools that were used gave very consistent results for the measured rings velocities and thus for the localspeci fic impulse.

1)The presented method was used to quantify the in fluence of the following burial conditions on the local speci fic impulse distribution:variation of embedding material(alluvial sand, quartz sand),depth of burial,water content and saturation.A very de fined and reproducible preparation of the embedding test bed was given specialattention.This is a requirement for a correct assessment of important in fluencing factors for the momentum transfer.

2)For the embedding materialalluvialsand,the speci fic impulse shows a distribution as function of the radial distance that resembles a Gaussian bell shape curve.The maximum speci fic impulse directly above the charge is 8 kPa·s and decays to a value of 4 kPa·s within a radialdistance of 70 mm.

3)For the embedding material quartz sand,the radial distribution of the speci fic impulse is broadened compared to alluvial sand with the highest value of 6 kPa·s at a radial distance of 70 mm.The speci fic impulse directly above the charge shows lower values around 5 kPa·s.

4)There is no clear dependency of the momentum transfer on the saturation.When the charge is embedded in quartz sand, the speci fic impulses are higher for the completely dry sand in the area above the charge than with saturation 32%and 66%. However,the two cases with a higher water content only differ slightly among each other.The experimentalresults can be used as a database for the development of numerical simulation models and the improvement of empiricalmomentum transfer models.

Acknowledgments

The authors want to thank TRDir K.Hüsing from the German test range WTD-91 GF-440 in Meppen and TRDir K.Neugebauer from BAAINBw for funding this work.

[1]Showichen A.Numerical analysis of vehicle bottom structures subjected to anti-tank mine explosions.Cran field University;2008.PhD thesis,https:// dspace.lib.cran field.ac.uk/bitstream/1826/2914/1/showichen_final_100708. pdf.

[2]Grujicic M,et al.Impulse loading resulting from shallow buried explosives in water-saturated sand.Proc IMechE 2007;221(Part I):21-34.

[3]Bergeron DM,Tremblay JE.Canadian research to characterize mine blast output,vol.16.Oxford:MABS;2000.

[4]Neuberger A,Peles S,RittelD.Scaling the response ofcircular plates subjected to loarge and close-range spherical explosions.Int J Impact Eng 2007;34: 874-82.

[5]Zakrisson B.Numerical simulations of blast loaded steel plates for improved vehicle protection.Lulea University of Technology;2013.PhD thesis,http:// ltu.diva-portal.org/smash/get/diva2:999223/FULLTEXT01.pdf.

[6]Fiserova D.Numerical analyses of buried mine explosions with emphasis oneffect of soil properties on loading.Cran field University;2006.PhD Thesis, https://dspace.lib.cran field.ac.uk/bitstream/1826/1209/1/darina% 2520fiserova.pdf.

[7]Williams K,McClennan S,Durocher R,St-Jean B,Tremblay J.Validation of a loading model for simulating blast mine effects on armoured vehicles.2009.

[8]Borvik T,Olovsson L,Hanssen AG,Dharmasena KP,Hansson H,Wadley H. A discrete particle approach to simulate the combined effect of blast and sand impact loading of steel plates.J Mech Phys Solids 2011;59:940-58.

[9]Laine L,Sandvik A.Derivation of mechanical properties for sand.In:Proceedings of the 4th asia-paci fic conference on shock and impact loads on structures.Singapore:CI-Premier PTE LTD;2001.

[10]Heider N,Klomfass A.Numerical and experimental analysis of the detonation of sand-buried mines.In:22nd international symposium on ballistics;2005. Vancouver.

[11]Anderson Jr CE,Behner T,Weiss CE.Mine blast loading experiments.Int J Impact Eng 2011;(38):697-706.

[12]Heider N,Denefeld V,Holzwarth A.Methods for the analysis of global IED effects on military vehicles.In:European survivability workshop;2010.Alesund,Norway.

[13]Clarke S,Fay S,Warren J,Tyas A,Rigby S,Reay J,Livesey R,Elgy I.Geotechnical causes for variations in output measured from shallow buried charges.Int J Impact Eng 2015;86:274-83.

[14]Clarke S,Fay S,Warren J,Tyas A,Rigby S,Reay J,Livesey R,Elgy I.Predicting the role of geotechnical parameters on the output from shallowed buried explosives.Int JImpact Eng 2017;102:117-28.

[15]Fox D,Lee J.The in fluence of water,dry sand,and unsaturated sand constitutive behavior on the blast response of a rigid target.Int J Impact Eng 2014;65:163-73.

[16]McShane G,Deshpande V,Fleck N.A laboratory-scale buried charge simulator. Int J Impact Eng 2013;62:210-8.

[17]Heider N,Denefeld V,Holzwarth A,S¨attler A,Salk M.Vehicle protection against global IED effects.In:27th international symposium on ballistics; 2013.Freiburg.

[18]Denefeld V,Heider N,Holzwarth A,S¨attler A,Salk M.Reduction of global effects on vehicles after IED detonations.In:28th internationalsymposium on ballistics;2014.Atlanta.

[19]Heider N,Denefeld V,Steinbrenner A,Holzwarth A.Engineering tool for the evaluation of global IED effects.In:29th international symposium on ballistics;2016.Edinburgh.

[20]Wenzel AB,Esparza ED.Measurements of pressures and impulses at close distances from explosive charges buried and in air.1972.SwRI-Report.

[21]Held M.Blast effects with the held momentum method.In:21st international symposium on ballistics;2004.Adelaide.

[22]Assaf A,et al.The in fluence of soil conditions on the blast intensity for sand, clayey sand and gravel with silt.In:28th international symposium on ballistics;2014.Atlanta,GA,USA.

[23]Rigby S,Fay S,Clarke S,Tyas A,Reay J,Warren J,Gant M,Elgy I.Measuring spatial pressure distribution from explosives buried in dry Leighton Buzzard sand.Int J Impact Eng 2016;96:89-104.

[24]Clarke S,Fay S,Warren J,Tyas A,Rigby S,Elgy I.A large scale experimental approach to th measurement of spatially and temporally localised loading from the detonation of shallow-buried explosives.Meas Sci Technol 2015;26: 015001.

[25]Zhao X,Tiwari V,Sutton M,Deng X,Fourney WL,Leiste U.Scaling of the deformation histories for clamped circular plates subjected to blast loading by buried charges.Int J Impact Eng 2013;54:31-50.

[26]Mullin S,Carpenter AJ,Riegel IIIJP,Cox PA,McFarland JM,Weiss C,Walker JD, Riha DS,Grosch DJ,Mathis JT.New analytical formulations for land minde total and speci fic impulse predictions.In:28th internation symposium on ballistics;2014.Atlanta.

[27]Westine P,Morris BL,Cox PA,Polch EZ.Development ofcomputer program for floor plate response from land explosions.1985.

[28]Tremblay J.Impulse on blast de flectors from a landmine explosion.Valcartier, Canada:Defence research establishement;1998.

16 January 2017

*Corresponding author.

E-mail address:vincent.denefeld@emi.fraunhofer.de(V.Denefeld).

Peer review under responsibility of China Ordnance Society.

http://dx.doi.org/10.1016/j.dt.2017.03.002

2214-9147/©2017 The Authors.Published by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

Received in revised form 10 March 2017

Accepted 17 March 2017

Available online 28 March 2017