Improved theory of projectile trajectory reference heights as characteristics of meteo-ballistic sensitivity functions

Vladimir Cech,Jiri Jevicky

aDepartment of Weapons and Ammunition,University of Defence,Kounicova 65,662 10 Brno,Czech Republic

bDepartment of Mathematics and Physics,University of Defence,Kounicova 65,Brno 662 10,Czech Republic

cOprox,Inc.,Kulkova 8,Brno 615 00,Czech Republic

Improved theory of projectile trajectory reference heights as characteristics of meteo-ballistic sensitivity functions

Vladimir Cecha,c,*,Jiri Jevickyb,c

aDepartment of Weapons and Ammunition,University of Defence,Kounicova 65,662 10 Brno,Czech Republic

bDepartment of Mathematics and Physics,University of Defence,Kounicova 65,Brno 662 10,Czech Republic

cOprox,Inc.,Kulkova 8,Brno 615 00,Czech Republic

A R T I C L E I N F O

Article history:

Exterior ballistic

Sensitivity analysis

Non-standard projectile trajectory

Green's functions

Weighting factor functions(curves)

Reference height of projectile trajectory

METEO-11(“meteo-average”)

Projectile trajectories calculated under non-standard conditions are considered to be perturbed.The tools utilized for the analysis of perturbed trajectories are weighting factor functions(WFFs)which are a specialkind of sensitivity functions.WFFs are used for calculation of meteo ballistic elementsμB(ballistic wind wB,virtual temperatureτB,pressure pB,densityρB,speed of sound a)as well.An effect of weapon system parameters can be incorporated into calculations through the reference height of trajectory-RHT. RHT are also calculated from WFFs.Methods based on RHT are far more effective than traditional methods that use weighting factors q.

We have found that the existing theory of RHT has several shortcomings due to we created an improved theory of generalized RHT which represent a special sensitivity parameters of dynamical systems.Using this theory will improve methods for designing firing tables,fire control systems algorithms,and meteo message generation algorithms.

©2017 The Authors.Published by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

1.Introduction

This contribution follows up on our earlier publications[1-5], but a detailed analysis of problems under consideration is presented in studies[6-8].For the sake of understanding of contents ofthis article,itis,at least,needfulto peruse problems ofweighting (factor)functions(curves)WFFs presented in Ref.[4].The traditional theory of the reference height of a trajectory RHT is elaborated in the article[1]predominatingly under utilization of the textbook[10].

We apologize for erroneously referred to signs in the article[4] in the relations(33-35).In the present article they correspond to the relations(2-4),in which the signs are placed correctly.Moreover,in Ref.[4]in the relation(45):before the square brackethas to be the right number-1.

1.1.Motivation

We continue in research with the same theme and therefore our motivation can not change[1-5]:It follows from the analysis of artillery fire errors,e.g.Refs.[9,10],that approximately two-thirds of the inaccuracy of indirect artillery fire is caused by inaccuracies in the determination of meteo parameters included in the error budget model[9].Consequently,it is always important to pay close attention to the problems ofincluding the actualmeteo parameters in ballistic calculations[10].The following meteo parametersμare primarily utilized:Wind vector w,air pressure p,virtualtemperatureτ,densityρ,and speed of sound a[10-13].

This paper deals only with problems relating to unguided projectiles without propulsion system for the sake of lucidity of the solved problems.

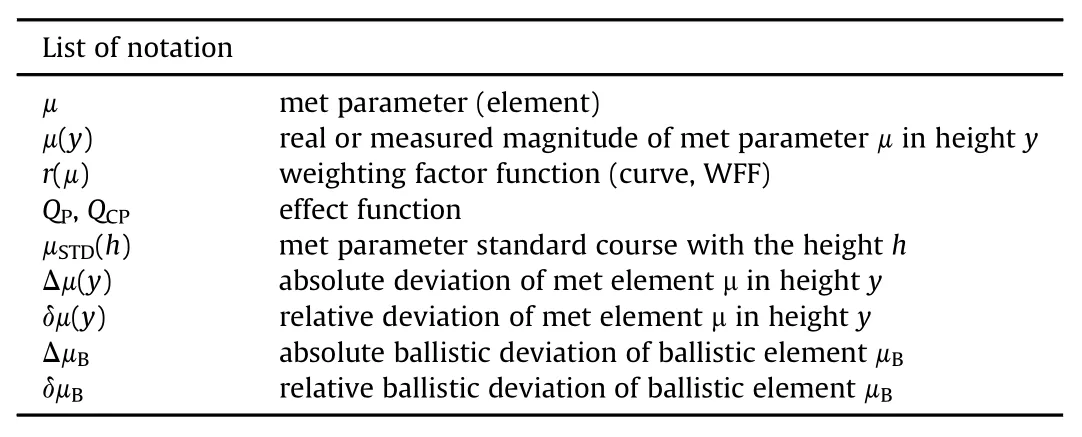
List of notation μ met parameter(element) μ(y) real or measured magnitude of met parameterμin height y r(μ) weighting factor function(curve,WFF) QP,QCP effect function μSTD(h) met parameter standard course with the height h Δμ(y) absolute deviation of met elementμin height y δμ(y) relative deviation of met elementμin height y ΔμB absolute ballistic deviation of ballistic elementμBδμB relative ballistic deviation of ballistic elementμB

1.2.References and terminology

The reference height RHT is only in use by the Soviet methodology,which is joined with utilization of the meteo message METEO-11(“Meteo-average”),and therefore references to this area are totally missing in publications which were published outside the former Soviet bloc.It is a problem that only the textbook[10] can be considered as quality.The next publications[14-20]give only a slight information which can serve to the understanding of basic properties of the reference height RHT and methods of its utilization.Only the article[20]deals with a new method for computation of the reference height RHT.

The new methodology was introduced(see Ref.[20])by the instruction: “Hаставление артиллерии советской армии, AртиллерийскаяметеорологическаяслуЖба,Mосква1956”(“Artillery Instruction of the Soviet Army,Artillery Meteorological Service, Moscow 1956”).Referred material is for us yet unavailable.The methodology was gradually introduced even in the 1960s and 1970s in the Soviet satellites.In the Soviet literature there is used the original designation for the RHT“высотавходавбюллетень“метеосредний””(“input height into bulletin“meteo-average””)or the short one“условнаявысота”(“conventional height”).The first designation is too long and the second one does not correspond to the physical nature of this quantity,therefore we decided to use other designations.The author of the articles[19,20]uses the sign“conditionalheight”,which is also not too appropriate.

1.3.The main objectives of the contribution

We have shown in articles[1-3]that the Soviet methodology for the use of the reference height RHT and the meteo message METEO-11(“meteo-average”)has a greater potentialfor increasing the accuracy ofthe calculation ofthe corrections on the in fluence of meteo parameters than the traditional methodology[21-26], which was introduced already in the 1910s and 1920s and which uses a system of weights q(μ)(weighting factors-WFs)derived from the relevant WFFs.The formation and use of the meteo message METBKQ[27]is based on this methodology and also the corresponding creation and use ofthe tabular firing tables-TFT in practice[28-33].The Soviet methodology used until 1956 was virtually identical,too.

If the METEO-11 is in use,then the weighting factors q(μ)are proportional only to the relative height of the individual zoneslayers.The effect of ballistic parameters of weapons and ammunition is then included in the calculations just by using the reference height of projectile trajectory-RHT YR,which is a multiple of the height oftrajectory(HT,Y=YS),thus YR=KR·YS,KR=cc.0.8 to 1.4. The values of RHT are together with HT given in the tabular firing tables for the relevant projectile and the charge depending on the range of fire.The reference heights RHT are calculated also from the relevant WFF.

In the meteo message METBKQ,the ballistics elementsμBare sought for the height of trajectory HT YScorresponding to the given range X,whereas in the METEO-11,the ballistics elementsμBare sought for the reference height RHT YRcorresponding also to the given range X.

We have shown in the article[4]that from the view of the modern theory of sensitivity analysis of dynamical systems,the WFFs are normed sensitivity functions,which provide concentrated information about the sensitivity of changes of projectiles trajectories on the perturbations of the relevant meteo parameters μ.

The weighting factors and the reference heights RHT are derived from the WFFs and therefore they also pertain to the sensitivity characteristics of the meteo-ballistic system.

In the available literature,there exists a semi-empirical de finition ofthe reference height RHT[10,19].We analyzed this problem in Refs.[1-3,6].An exact de finition has not yet been published.

The main contribution ofthe article is an exact derivation ofthe de finition relationship for the reference height RHT-the relation (40).This relation de fines the generalized RHT[7,8],whose special case is the traditional RHT.

In practice,three perturbation models are used for the calculation of the WFFs[26,4].The soviet methodology uses a model formulated by Frenchman P.Langevin[4,10,26].In this case,the WFFs are without the norm effect or with a weak norm effect, therefore,the authors of the originaltheory of the reference height of trajectory(RHT)at all did not deal with problems of the norm effect.

Our goalwas to modify the theory of RHT so as to be applicable even for perturbation model for the calculation of the WFFs used initially in the USA and now also in NATO[23,25,26].It is typicalfor this model that some WFFs are with the strong and exact norm effect-paragraph 1.4.2.In this case,division by zero or by very small numbers occur in the calculations.

The practicalconsequence is that the calculation ofrespectively corrections and gradients for the numerical iteration in a neighbourhood of a strong norm effect and the exact one,either completely fails,or is very inaccurate.

Our contribution is that we can control the whole process of numerical calculations so that the needed accuracy should be achieved also in areas with strong and exact effects.Whereas,it is given“only”by the fact,thatas a parameter,in allformulas,there is performing consistently the value r(1)as a measure ofthe intensity of the norm effect.

Subsequently,we analyze three ways ofnumericalcalculation of the generalized reference height RHT:

-our originalprocedure based on the de finition relationship(40) -the paragraphs 2.2 and 2.3,

-the originalprocedure modi fied by us[6-8,10]-the paragraph 3.3.and relationship(65),

-the procedure proposed by Petrovic in Ref.[20],which we also generalized[8]-the paragraph 4.1.and relationship(72)and the paragraph 4.2.and relationship(78).

The published results allow generalizing of the original soviet methodology and widely putting into practice.

1.4.Weighting functions-basic information

In this paragraph,we brie fly present findings from our article [4],which are necessary for the understanding ofthe subsequently presented theory of the reference heights RHT.

1.4.1.Green's functions ofthe projectile trajectory sensitivity models

The best way to analyze the characteristics of the projectiles trajectories under nonstandard conditions is the build of any of the explicitsensitivity models ofprojectile trajectory[21,23,25,26].The talk is then about the(differential)sensitivity analysis ofdynamical system(projectile trajectory)or about the parameter sensitivity analysis or aboutthe sensitivity ofa system to parameter variations.

The perturbation theory is often used to the build of these models[34,35].These are the linearized models represented by systems of linear differentialequations with variable coef ficients.

Relations between generalized inputs(control input variables, disturbance input variables and variable parameters of the system) zm(t),m=1,2,…on one side and output variables yl,l=1,2,…on the other hand,are given traditionally by transfer functions and Green's functions gm,l(t-tP).There is also a generalized theory ofGreen's functions for some groups of non-linear systems.

In our case,we take into consideration only the following generalized inputs:the wind vector w=(wx,wy,wz)as a disturbance input variable and next variable meteo parameters(the virtual temperatureτ,the air pressure p,the air densityρand the speed of sound a).Allwe denote,as we have already noted,by the common symbolμ.In the case of other parameters ofthe modelof the projectile trajectory,it progresses as well.

The most important output variables are the coordinates of the partially perturbed projectile trajectory(x,y,z)and corresponding time of flight t.

Green's functions are also denoted as weight or weighting functions or in fluence functions or impulse response functions.In the case of sensitivity models of a dynamical system,the Green's functions represent specialsensitivity functions of two parameters (t,tP):

t is the momentto which the system response willbe calculated. In our case,it is the moment of tPIin which the standard projectile trajectory passes through chosen point of impact/burst with coordinates(t,x,y,z)PI.According to its position on the projectile trajectory,we distinguish four types of the projectile trajectories [4].

tPis the moment in which to impress zm(t -tP)=zm(t)+Δzm0·δ(t-tP),where zm(t)is unperturbed quantity, Δzm0is the amplitude of excitation andδ(t-tP)the unit impulse (the Dirac delta function).We distinguish three types oftrajectories of the projectile:

-partially perturbed trajectory,if tP∈ (0,tPI)and its special variants:

-(full)perturbed trajectory),if tP=0,i.e.the impulse impresses at the beginning of the trajectory and

-the standard(unperturbed)trajectory,if tP≥tPI.

In the exterior ballistics there are used(traditionally from the 1910s)the effect functions Rm,las the response to the excitation zm(t-tP)=zm(t)+Δzm0·H(t-tP),where zm(t)is unperturbed quantity,Δzm0is the amplitude ofthe excitation,and H(t-t p)is the Heaviside step function.

The normed effect functions are denoted as the weight or weighting functions,it is therefore a different terminology due to the theory of dynamical systems.To differentiate them from the Green's functions,we will refer to weighting(factor)functions (curves)WFFs rm,l[10,14-21,23,25,26].

Due to the properties of the Dirac delta function and the Heaviside step function,the following relationship applies[4,7]

where

Nmlis the relevant norm-see the paragraph 1.4.2.and σml=+1 or-1 is the contractualsign-see the paragraph 1.4.2.

It follows from this relation that not only the Green's functions are sensitivity functions,but also the effect functions Rm,land the weighting functions WFFs rm,lare sensitivity functions,too.

In practice[4,7],the functions QPm,l=Δzm0·Rm,lare taking rather than the functions Rm,l,and they are also referred to as effect functions.We will use mentioned functions hereafter and we will denote them QP(μ,tP)=QP(μ)=QP(tP)=QP[4,7,10].Under this designation,we understand especially special shapes of the perturbation of the output quantitiesΔyl:ΔX(μ,tP),ΔY(μ,tP), ΔZ(μ,tP)aΔt(μ,tP).The values are relative to the moment tPIin which the standard trajectory passes through the point of impact/burst[4,7].It willbe assigned to the functions QP(μ,tP)the norm Nm,land the signσml,we will denote them NQandσQhenceforth.

The effect functions QP(μ,tP)and the corresponding weighting functions WFFs r(μ,tP)are functions of two times(tPI,tP)and the corresponding meteo parameterμ(tP),which is subject to the perturbation.In the basic variant of analyses,we assume that only one selected meteo-parameter is subject to the perturbation.

The totalperturbation QPS(Δμ)ofthe parameters of the point of impact/burst,e.g.the rangeΔXP(Δμ)-if the course ofthe absolute deviationsΔμ(t)from the standard values is known(measured), Δμ(t)=μ(t)-μSTD(t)-is given by the convolutory integral[4,7]

where

μSTD(t)is the standard course of the meteo parameterμ,

ΔμB0=const is a contractual value[4,7],

ΔμBis the absolute ballistic deviation/perturbation of the ballistic meteo parameterμ (e.g.ballistic range/cross wind (wx,wz)B,absolute ballistic virtual temperature deviation/ perturbationτB,etc.).

Analogous relations to(2)and(3)also applies for the known (measured)relative deviationsδμ(t)(δμ(t)=Δμ(t)/μSTD(t))[4,7].In that case,the effect functions and WFFs willhave index R(relative deviationδμ)instead of the index A(absolute deviation(perturbation)Δμof the meteo parameterμ),i.e.QPR,rR.

All the following considerations are identical for respectively the absolute and relative deviations(perturbations)of the meteo parameterμ,therefore,we will do the derivation only for the variant“absolute deviations(perturbations)Δμofmeteo parameter μ”,while the index A will be omitted.

Measured deviations are evaluated for the requirements of the flat-fire depending on the topographic range,i.e.,on the coordinate x,and so(Δμ(x),δμ(x))is used[4,7].As a consequence,the equations(2)and(3)must be modi fied.

We willuse the function tP=F(x),which is valid for the standard trajectory;then it will be QP(μ,x)and r(μ,x).Let us remind the reader that d x=vx·d tP,thus the equation(3)will have the form

We choose(σQ·NQ)= QP(μ,x)for x=0 in all cases (NQ=abs(QP(0))),σQ=sign(QP(0)).

The WFFs for the range wind rwx(x)and for the cross wind rwz(x) are important only for the flat-fire from a practicalpoint of view.

For shooting at common trajectories,measured deviations (Δμ,δμ)are evaluated depending on coordinate y of the projectile trajectory,thus(Δμ(y),δμ(y))is used[4,7].Therefore it is necessary to modify the relations(2 and 3)again.

It was newly created a generalized theory of the generalizedeffect functions QCP(μ,tP)and the generalized WFFs rC(μ,tP)[4,7].

From the generalized effect functions QCP(μ,tP)are successively calculated generalized Garnier's effect functions QCG(μ,y)and generalized Bliss'effect functions QCB(μ,y),which are already functions of the vertical coordinate y[4,7].This conversion relationship holds

The value QCG(μ,y0)represents the cumulative effect of all perturbations in heights y≥y0and the value QCB(μ,y0)represents the cumulative effect of all perturbations in heights y≤y0.

Generalized weighting factor functions WFFs are calculated by norming from generalized effect functions(curves).

For generalized Garnier's weighting factor functions WFFs it holds that[4,7]

For generalized Bliss'weighting factor functions WFFs it holds that[4,7]

where

where

ymin=min(y(t))and ymax=max(y(t))for t∈〈0,tPI〉.

QCG(μ,ymin)=QCP(μ,ymin)=QCP(μ,tP)=QCP(tP)for tP=0 and rCG(ymax)=r CB(ymin)=0.

Furthermore the relationship holds

According to NATO and Soviet methodologies using Bliss'WFFs rB(μ,y)are presupposed,so we willlimitour following analysis only to generalized Bliss'WFFs rCB(μ,y).Ifinterchange is notpossible,we will no longer mention index“CB”in description of WFFs.

However,the generalized Garnier's WFFs are preferable for analyses and graphical display of the so-called“norm effect”(see the paragraph 1.4.2).

Analogically for relations(2 and 3),(d y=vy(tP)·tP)will apply [4,7]

It is convenient to introduce the following normalization of the vertical coordinate y

where

h=hG+y is the altitude corresponding to the vertical coordinate of the y,

hGis the altitude of the horizontal plane(x,z),y=0 of the ballistic system,

Δh=h-hmin=y-yminand

Δhm=hmax-hmin=ymax-ymin.

After the introduction of this transformation,the convolutory integral(9)goes into the form[7,8]

Convolutory integrals,which are given by the relations(3),(4), (9)and(11),can be also understood as the calculation of the weighted averageΔμBofthe quantitiesΔμ(.).The weightfunction is always the fi rst derivative of the relevant WFFs and that is simultaneously the corresponding sensitivity function-the normed Green's function-see the relation(1).

A special case is the calculation of the arithmetic average. In this case,the WFFs have a speci fi c form r=1-(tP/tPI),resp. r=1-(x/xPI),resp.r=η=(y-ymin)/(ymax-ymin).

1.4.2.Normalization of Green's functions.Norm effect

For simplicity,we will only deal with the normalization for WFFs dependent on the vertical coordinate respectively y andη, and for the notation introduced by Bliss(generalized Bliss'WFFs).

The normalization is based on the relationship for the full perturbed trajectory[4,7]

In the case of the traditionalnormalization,the choose r(1)=1 (as a de fi nition)is prevalent and then

while it is traditionally tacitly presumed that it holds d r(μ,y)/ d y≥0,then r(μ,y)∈〈0,1〉.

Ifthis tacit assumption d r(μ,y)/d y≥0 is not ful fi led,i.e.that for a certain range of values of y it holds d r(μ,y)/d y＜0,then also the implication r(μ,y)∈〈0,1〉does not hold.It can hold that min(r(μ,y))＜ 0 and/or/simultaneously max(r(μ,y))＞ 1,i.e. r(1)＜max(r(μ,y)).The described state is called the“norm effect”[4,7,25].

An exact norm effect,however,occurs in the case that the QP(μ,0)=0.Justthen,the traditionalnormalization can notbe used at all.

It is quite common for WFFs for virtualtemperature rτ/ρ,which expresses only the in fl uence of the“elasticity”of the air,i.e.the effectofthe virtualtemperatureτon the size ofthe drag coef fi cient cD(M)through the Mach number,resp.the speed of sound a [4,7,25].The method of normalization for this case,which is proposed in Ref.[25],is mathematically correct,but for practical use inappropriate.

We have proposed therefore the following norm[4,7],see the equation(7)

and at the same time

if it applies that QCP(tP)≠0 for tP=0,i.e.QCP(0).

If QCP(0)=0 then a number ofvarieties how to chooseσQexist. For example we can choose[4,7]

where

In case that expression r(1)=max(r(μ,y))and min(r(μ,y))=0 holds,the relations(13)and(14)consistent with the traditional relation(12).

Illustrative figures to the exact norm effect are presented in Refs.[4,7].

If it is not the exact norm effect(QP(μ,0)≠0),the both norms given by relations(13)and(15)can be used.Then it is possible proceed in two steps[8]

In the first step,we use the traditionalnormalization according to equation(13),i.e.r(1)=1.Subsequently,we calculate the course of WFFs r(μ,η)and we determine the norm

which is analogous to the norm according to the relation(15).

In the second step,we calculate the new weighting function

for which itholds rN(1)=1/Nrinstead ofthe original r(1)=1.In this case,it holds instead of relation(12)

and the norm of this new WFFs rN(μ,η)is equal to one(Nr=1).

Ifthe norm Nr＜εandε＜cc.(5-10),then the traditionalnorm is better for use(no or weak norm effect).In the opposite case,the norm NQ1relatively small and in the traditional normalization we divide a number close to zero(strong and exact norm effect).

The following division of the WFFs can be made(r(1)=rN(1)∈〈0,1〉)

-WFFs without the norm effect(r(1)=1),

-WFFs with a weak norm effect(r(1)＞cc.0.2),

-WFFs with a strong norm effect(r(1)＜cc.0.2),

-WFFs with the exact norm effect(r(1)=0).

The problem is illustrated by the help of Figs.1 and 2.

2.Generalized reference Height

The traditional reference height RHT is de fined only semiempirically in the textbook[10].In this section,we derive an exact de finition of the generalized reference height gRHT[8].The traditional reference height is a special case of the generalized reference height gRHT.

2.1.Approximation of measured meteo-ballistic data

2.1.1.Basic information

We approximate a measured course ofΔμ(η)by a polynomialof n-th degree using e.g.the least squares method

where

n is the degree ofthe polynomial.The chosen degree depends on the desired accuracy of the approximation.

aiare the approximation constants-coef ficients of the approximating polynomial.

In fact,it is necessary to proceed somewhat more complicated. The measured dataΔμ(h)are determined in dependence on the verticalcoordinate(superelevation)yz,wherein

where

h is the altitude in which theΔμ(h)is measured, hMDPis the altitude of the meteo station(Meteorological Datum Plane).

The measurement ofΔμ(yz)takes place to the superelevation yzm,i.e.yz∈〈0,yzm〉.The maximum superelevation value is usually 30 km(yzm≤30 000 m).It is normally yzm=15 000 m[10,28,29].

We willdo only one approximation of the course ofΔμ(ηz)

where

Such approximation can be easily obtained from the data given in the meteo message METCMQ[28,36]from which we can calculate the corresponding courses ofΔμz(ηz)that can be subsequently approximated by the formula(23).

We determine the coef ficients aiby a conversion from the coef ficients azi.For this,we use the link between the coordinates (relations(10 and 22))

where hZG=hG-hMDPis the gun superelevation above MDP.

To find the approximation(23),it is convenient to use procedures based on the use oforthogonalfunctions.The shifted Legendre polynomials(de fined on the interval〈0,1〉)appear as the most advantageous.The Chebyshev or Laguerre polynomials can be also used.For the analysis of the wind can be useful to use the Fourier series,too.These problems are not the subject of this article.

2.1.2.Average meteo-data

In the meteo message METEO-11(“Meteo-average”)there is indicated the arithmetic average of the absolute and relative deviations of the meteo data[10,14-20].

In general,it holds for the average absolute deviationΔμAV(y)of the meteo parameterμon the interval〈ymin,y〉[7,8]

An analogous relationship is true also for the average relative deviationδμAV(y)ofthe meteo parameterμon the interval〈ymin,y〉, whileδμAV(y)=δμAV(h)=Δμ(h)/μSTD(h).The relative deviations for the wind are not de fined.

After substituting relation(21)into(25)and the adjustment,we obtain the approximate relationship for the average absolute deviationΔμAV(y)of the meteo parameterμon the interval〈ymin,y〉[7,8]

where

bi=ai/(i+1)are the new approximation constants-coef ficients of the approximating polynomial.It is clear from the relation between aiand bithat averaging is a specialcase ofthe low frequency filtration of the input/output signalΔμ(y).

In the case of the absolute deviations given in the METEO-11 (meteo-average),the analogous approximation to(26)derived from(23)is valid

where

bzi=azi/(i+1)are the new approximation constants-coef ficients ofthe approximation polynomial.It is again obvious from the relationship between aziand bzithat the averaging is a special case of low-frequency filtration of the input/ouput signalΔμ(y).

It is therefore obvious that we can proceed the other way around.Firstly we approximate the pre-calculated average absolute deviationΔμAV(y)ofthe meteo parameterμon the interval〈ymin,y〉, to which we can use,for example,the data referred to in the METEO-11(“Meteo-average”).So primarily we obtain the coef ficients bziand biand only subsequently we can calculate the size of the coef ficients aziand ai.

2.2.Moments of weighting factor functions

If we substitute into relation(11)the expression(21),then we receive after integration and adjustment the working relationship for the absolute ballistic deviation/perturbationΔμBof the meteo parameterμ[7]

mWFF,i,i=0,1,2,…,n,are the normed moments of the first derivative of the weighting function WFF r(μ,η),so the normed Green's function.They are therefore the characteristics of the sensitivity function.

For the first two normed moments apply

and

The use of normed moments of the first derivative of the weighting function WFF has notyet been published in the available literature.

If we substitute into relation(11)the expression(26),then we receive after integration and adjustment a working relationship for the absolute ballistic deviation/perturbationΔμBof the meteo parameterμ[7]

Most of the weighting functions WFF r(μ,η)is determined numerically,so they are known only their discrete values rj=r(μ,ηj),j=0,1,….If we use for the numerical integration of the relation(28)the rectangular rule,we obtain the following working relations for the determination of the normed moments of the first derivative of the weighting function WFF

where

qj=rj-rj-1=r(μ,ηj)-r(μ,ηj-1)are the discrete weights/weight numbers(weighting factors)WFs for the j-th layer/zone [1,6,8,10,19,22,24-29],

Δηj=ηj-ηj-1relative height of the j-th layer/zone.

For example,it is true for the weight function WFF,derived under assumption,that the projectile trajectory is approximately equalto the projectile's trajectory in a vacuum[1,6-8,10,24,26]

The normed moments of the first derivative of the weighting function WFF mWFF,j,j=0,1,…,5 for this relationship,calculated using the formula(35)with the stepΔη=0.002,are 1;0.6666; 0.5333;0.4571;0.4063;0.3693.

For the WFF(r(1)=1)in the Fig.1,itholds accordingly 1;0.7970; 0.6334;0.5303;0.4585;0.4048.

2.3.Generalized reference height of projectile trajectory

We use the linear approximation[8]for the absolute ballistic deviation/perturbationΔμBof the meteo parameterμunder utilization of the relations(31,33,34)

We make the following hypothesis:For the generalized reference height YCR,respectively,for the correspondingηCRmust be true

By comparing the relations(37 and 38),we obtain the relationship for the coef ficient of the generalized reference height[8].

and it holds for the generalized reference height[8].

Relations(39,40)represent an exact de finition of the generalized reference height YCRand are the result of our research.They have not yet been published.This is a characteristic of the sensitivity function-the normed Green's function.

In the case that ymin=0,thenΔhm=ymaxand the relationship (40)de fines the reference height YRin the traditionalconcept[1,10].

The second member of relation(39)will be zero in two cases:

-if it will be used the traditional standardization(relations (13,14),r(1)=1)-this requirementcan be satisfy,ifrespectively no strong and no exact norm effect is generating-the paragraph 1.4.2.

-ifit willbe true specially,that a0=0.This can be achieved,ifwe use the regression function(relation(21))in the special form Δμ(η)=a1·η.

If a1=0,then immediatelyΔμB≈a0.

As we stated in the paragraph 2.1.1,the measured meteo data are recorded in dependence on the verticalcoordinate yzin the meteo messages,then it is preferable to find a relationship for the generalized reference height YCR,z,transformed to the coordinates yz[7,8,10].We derive the transformation relationship now.The approximate transformation relationship now we derive with the use of Fig.3.

First we find the transformation relations between the(az0,az1) and(a0,a1)-relations(21,23 and 10)assuming that the approximations are linear.Substituting for yzcorresponding values of y given by the equation(24)into the linearized equation(23)we obtain the two approximations

Because this is about the same altitude,or the ordinate y,both expressions must equal each other.From the equality of the expressions and by comparing term by term we obtain the transformation relations

where

ΔhZ,m=hZG+yminis the linear shift of the origin of the coordinate system yzandΔh,further ymin≤0[4,7,8].

We make the hypothesis that it approximately applies

Now we compare the relations(38 and 45)using(40)and simultaneously we account the relations between the(az0,bz0)and (a0,b0),(az1,bz1)and(a1,b1)given by(26 and 27).

We receive a wanted approximate transformation relationship

where

ΔYCR,z=2·ΔhZ,m=2·(hZG+ymin)is the repair ofthe generalized reference height,ymin≤0.This is a generalization of the relation cited in the literature[10,14,16,18]for the case ymin=0.

Search for the absolute ballistic deviation/perturbationΔμB,in the meteo message METEO-11(meteo-average),is performed in two approximate ways.

In the first case,it approximately applies

In the second case,the first performs a transformation ofallthe coordinates yzin the meteo message

and subsequently approximately applies

In both cases,the calculation of the regression coef ficients bz0=az0and bz1=az1/2(the relation(23))at alldoes not perform.

According to the traditional recommendations(ymin=0)is taken,thatΔYCR,z=0,if abs(hZG)≤200 m[7,10,14,16,18].

Itfollows from the Fig.3 thatan approximation ofΔμz(yz)can be also used.We obtain this approximation from the data given in the meteo message METCMQ[28,36](and also see the comment to the relation(23)),while the estimate of the value ofΔμBwe calculate for yz=YCR,z/2.

3.Alternative relations for the determination of ballistic deviations

The aim is to find convolutory integralanalogous to the relation (11)in which would perform the average absolute deviation ΔμAV(η)instead of the measured absolute deviationΔμ(η).

3.1.Alternative analytic relation

In the derivation we use the two basic relations[7].

The first relation is a differential equation for theΔμAV(η)obtained by the differentiation of the relation(25)

The second relation is a well-chosen expression[7].

We derivative this expression so that we could use the method of integration by parts.To the resulting expression we substitute relation(50)and after adjustment we obtain[7].

We substitute the expression(52)into the relation(11)and perform the integration,so we obtain a new relation for the absolute ballistic deviation/perturbationΔμBof the meteo parameter μ[7]in dependence on theΔμAV(η)

This formula is notcited in the literature.The relationship is the result ofour research.Its use is strongly restricted by the necessity to carry out for the majority of the WFFs limit transitions in the derivation of working relations.

3.2.Numericalapproximation formula

The formula(53),although not in the literature cited,yet its numericalversion is given in Ref.[10].The following procedure[7] corresponds with the procedure referred to in Ref.[10].

We go out of the relationship(11)and the expressions for the weighting factors q-the relation(35),then

The integral in this relation can be with the use of the relation (25)expressed in the form

We substitute the expression(55)into(54)

Now we do rearrange the members in the sum,so as to create terms with the sameΔhjand finally we pass from the variableΔh to the variableη.So we get the following generalized expression for the numerical estimate of the absolute ballistic deviation/perturbationΔμBof the meteo parameterμ[7]

The formula(57)is a numeric version of the relation(53).

3.3.The traditional relationship for the reference height

We obtain the relations for the reference height YRalso by adjusting the relationship(57)[7,10].We generalize the procedure that we used in the article[1]and the related study[6].

The basic simpli fication lies in the fact that the WFF is approximated only by using the two weighting factors WFs q12,q22for intervals〈0,ΔhRR〉and〈ΔhRR,Δhm〉,i.e.m=2 in the relation(57). Two valuesΔμAV(ΔhRR)andΔμAV(Δhm)follow from the relation (25).At the same time the only two options(q12=0 and q22=1)or (q12=1 and q22=0)hold good.The aim is to find the appropriate approximation relations for the heightΔhRR.

We introduce the estimates of the partial derivatives

and put them into relation(54)

After the adjustmentwe receive the basic calculation relationship for the numerical estimate for the absolute ballistic deviation/ perturbationΔμBofthe meteo parameterμ((q12=0 and q22=1)or (q12=1 and q22=0))

where

it is the averageΔμAV(Δh)in the interval〈ΔhRR,Δhm〉.

Finally,we determine the area under the WFF

Further analysis leads to the derivation of the two valuesΔhRRandΔhR2for the concave shape(q12=1,q22=0,S≥ 0.5; ΔhRR=ΔhR2)of the weighting function WFF-Fig.4 andΔhR1for the convex shape(q12=0,q22=1,S＜0.5;ΔhRR=ΔhR1)of the weighting function WFF-Fig.5.Finally,it is derived another relation for the generalized reference height[7]

The relationship(65)is a generalization of the relations derived in Refs.[1,6,10].

A deeper analysis of given problems can be found in Refs.[1,6,10].So far,we did not check the accuracy of the relationship for the case of the existence of a norm effect-see the paragraph 1.4.2.

4.Generalized Petrovic algorithm for the reference height calculation

In the article[20],Petrovic suggested an effective algorithm for the calculation ofthe rereference height.Itis notnecessary to count the whole course ofthe WFF or its firstderivative,butitis suf ficient to calculate the projectile trajectory only three times.He deduced the competent relationship by an intuitive reasoning.In this section,we derive the competent relationship correctly and-in addition-we generalize Petrovic algorithm for the calculation of the moments of the first derivative of the WFF.

4.1.Generalized Petrovic algorithm

We willnot proceed completely in general,but we willconsider only the perturbation of the rangeΔX(μ)at a constant height of impacts of the projectiles(ΔY(μ)=0,the iso-height perturbations [4,7]).

To calculate the reference height YCR,it is suf ficient to calculate the projectile trajectory only three times.The first track is standard (unperturbed,paragraph 1.4.)calculated forμ(η)=μSTD(η).The next two tracks are fully perturbed and are calculated for the following courseμ(η)

Δμ0=Δzm0=const the excitation amplitude-the relation(1), more closely[4],

φj(η)are two special choices of approximation according to relation(21),j=0,1.

By calculations we get the ranges-the standard XSTDand two fully perturbed X0and X1.Models with 3,4/5 or 6 degrees of freedom(DOF)can be used to the calculation.Subsequently,we calculate the(full)perturbation of the trajectory

The relations(69-71)constitute a system of two equations in one parameter mWFF,0=r(1)and the one unknown mWFF,1.We search the solution provided that a10=0,then

This relationship is a generalization of the relation(77),which was derived by Petrovic with an intuitive technique.The relationship is only valid provided that a11≠0 and an exact norm effect does notoccur(r(1)=0 andΔX0=0).We do notrecommend to use it,ifa strong norm effect arises(r(1)→0).Petrovic probably didn't know anything aboutthe norm effectand unwittingly assumed that r(1)=1 andΔX0≠0[20].

We express mWFF,1=r(1)·KCR,1from the relation(72)and substitute it into the relation(39),then

Ifthe traditionalstandardisation willbe used(r(1)=1),itwillbe

In accordance with the Petrovic we choose

then the relation(72)goes over into the shape

If r(1)=1,then the relation(74)will have a special shape

Petrovic derived this relationship by an intuitive procedure. Petrovic further assumed traditionally in the relation(40)that Δhm=YS.

Our exact derivation shows that the relation(77)is only a special case of the relation(73),which respects the existence of the norm effect.

If we know the generalized reference height YCR(relation(40)) and the heightΔhm,then the KCRcan be calculated.If we know moreover r(1)and the coef ficients aij,i=0,1;j=0,1,e.g.according to(75),and if we calculated or acquired the valueΔX0from the Tabular Firing Tables,then the sizeΔX1can be calculated easily from the relations(72,73).

4.2.Effective algorithm for the calculation of the WFF moments

We don't know,if Petrovic knew,that the coef ficients(75), which he used,are the coef ficients ofthe first two shifted Legendre polynomials.It inspired us to a generalization of the algorithm described in the previous paragraph.

If we use the first(n+1)shifted Legendre polynomials as the functionφj(η),j=0,1,…,n in relations(67 and 68),and we calculate(n+2)projectiles trajectories,from which one standard and(n+1)perturbed(calculation ofΔXj,j=0,1,…,n),then it can be calculated by indicated way the n moments mWFF,j,j=1,2,…,n, if r(1)≠0.

In the case that r(1)=0(the exact norm effect),a parametric solution can be found and ifwe know one nonzero moment mWFF,k, k≠0,then we can calculate the remaining(n-1)moments.

Implied procedure[8]is numerically very economical and has not yet been published anywhere.It is about the generalization of the system of two linear equations(69)and(70)to the system of (n+1)equations

where

aijare the coef ficients of the first(n+1)shifted Legendre polynomials.The coef ficients form the matrix of the system A,that it is a lower triangular,so the solving the system(78)is algorithmically undemanding.

5.Conclusion

In this contribution and in the article[4],we have presented the core ofthe improved theory ofgeneralized WFFs and their moment characteristics,speci fically generalized reference height of trajectory,as a specialsensitivity functions.

This theory allows to perform an effective sensitivity analysis of the properties ofnon-standard projectile trajectories.The theory is fully linked to the more general theory of sensitivity analysis of dynamical systems,so the results can be interpreted in a broader context.

The theory of generalized reference height YCRpublished in this contribution creates the potentialfor a major simpli fication and an improvement in the calculations of corrections on the changes of the meteo ballistic parametersμcompared to the traditional method[10,14-18,22-29,32,33]using the tabulated values of the weighting factors q and which is used almost unchanged since the 1920s.Ourcreation ofconditions forthe extension ofthe use ofRHT even to the perturbation modelused in NATO,is important bene fit.

The theory of generalized reference heights assumes that data about the meteo parameters processed according to the methodology of formation of the METEO-11(“meteo-average”)are available.The principle of this methodology was clari fied in this contribution and the articles[1,4].The necessary initialdata can be simply calculated from the data given in the meteo message METCMQ[36](wind vector w(yz)and virtualtemperatureτ(yz)for yz∈〈0,yzm〉,pressure p0,MDPat MDP level).

In the next period,we plan to publish the contributions to the problems of the numerical calculation of the WFFs,since it is associated with a number of non-trivialinconveniences.

Consequently,we willcontinue in the research ofthe evaluation of the accuracy of the published algorithms.

Acknowledgments

This work originated with the support of financing from the Research Project for the Development of the Department of Weapons and Ammunition,Faculty of Military Technology,University of Defence,Brno,DZRO VYZBROJ.

[1]Cech V,Jedlicka L,Jevicky J.Problem of the Reference Height of the Projectile Trajectory as a Reduced Meto-ballistic Weighting Factor.Defence Technology 10,Number 2(June 2014),Issue 2:Special issue of the 28th International Symposium on Ballistics,ISSN:2214-9147,p.131-140.

[2]Cech V,Jedlicka L,Jevicky J.Problem of the Reference Height of the Projectile Trajectory as a Reduced Meto-ballistic Weighting Factor.Extended Abstract. Proceedings of the 28th International Symposium on Ballistics,Editors:Ames, R.G.,Boeka,R.D.,Atlanta,September 22-26,2014,p.7-10.

[3]Cech V,Jedlicka L,Jevicky J.Some Problems with the Estimation of Projectile Trajectory Perturbations.Proceedings of 20th International Conference Engineering Mechanics 2014,Book of full texts,Editor:Fuis,V.,Svratka,May 12-15,2014,p.116-119.

[4]Cech V,Jevicky J.Improved theory of generalized meteo-ballistic weighting factor functions and their use,Defence Technology 12(June 2016),Issue 3: Special issue of the 29th International Symposium on Ballistics,ISSN:2214-9147,p.242-254.

[5]Cech V,Jevicky J.Improved theory of generalized meteo-ballistic weighting factor functions and their use,Extended abstract.Proceedings of the 29th International Symposium on Ballistics,Volume 1,Editors:Woodley,C.,Cullis, I.,Edinburgh,May 9-13,2016,p.92-95.

[6]Cech V.Perturbation model of the projectile trajectory(in Czech).Research report.Brno:University of Defence;2014.p.114.

[7]Cech V.Reference height of the projectile trajectory(in Czech).Research report.Brno:University of Defence;2015.p.128.

[8]Cech V.Meto-ballistic corrections of the projectile trajectory(in Czech). Research report.Brno:University of Defence;2016.p.57.

[9]STANAG 4635 The NATO Error Budget Model.

[10]Kovalenko VV,Shevkunov VI.Meteorological preparation of artillery fire(in Russian).Leningrad:Military Artillery Academy of M.I.Kalinin;1975.p.84.

[11]Zipfel PH.Modeling and simulation of aerospace vehicle dynamics.2nd ed. Reston,VA,USA:AIAA,Education series;2007.p.607.

[12]Bockarev AF,Andrejevskij VV,Belokonov VM.Aeromechanics of the aircraft. Dynamics of flight(in Russian).Mashinostroyenie,Moscow.1985.p.360.

[13]Golubev IS,Svetlov VG,et al.Design of anti-aircraft missiles.2nd ed.Moscow: MAI;2001.p.732.

[14]Logvin AM,Aleksandrov VI.Gunnery and exterior ballistics(in Russian). Penza:Military Artillery Academy of N.N.Voronov;1977.p.255.

[15]Konovalov AA,Nikolajev Ju V.Exterior ballistic(in Russian).CNII;1979.p.228.

[16]Composite authors.Del-55-26 fire and fire control of the field artillery(in Czech).[Textbook].Prague:Ministry of Defence of the Czechoslovak Socialistic Republic;1981.p.856.

[17]Dmitrijevskij AA,Lysenko LN,Bogodistov SS.Exterior ballistic(in Russian).3rd ed.Moscow:Mashinostroyenie;1991.p.640.

[18]Lysenko LN,Benevolskij SV,Burlov VV,Kazakovcev VP,et al.Ballistics.Textbook(in Russian).Penza:Artillery engineering institute of Penza;2005. p.512.

[19]Petrovic DR.Mechanized procedure for the calculation of altitude coef ficients. In:Scienti fic-technical review,LV;2005.p.9-14.No.3-4.

[20]Petrovic DR.New procedure for calculating altitude coef ficients.In:Scienti fictechnical review,LVI;2006.p.47-51.No.3-4.

[21]Bliss GA.Functions of lines in ballistics.In:Transactions of the American mathematical society,vol.21;Apr.1920.p.93-106.No.2.

[22]Cranz C.Textbook of ballistics.First volume.Exterior ballistics(in German). 5th ed.Berlin:Springer Verlag;1925.p.712.

[23]Bliss GA.Mathematics for exterior ballistics.London:John Wiley and Sons, Inc.;1944.p.128.Printed in USA.

[24]Curti P.Introduction into exterior ballistics(in German).Verlag Huber and Co., Frauenfeld;1945.p.408.

[25]McShane EJ,Kelley JL,Reno FV.Exterior ballistics.Denver:University of Denver Press;1953.p.834.

[26]Molitz H,Strobel R.Exterior ballistics(in German).Berlin:Springer-Verlag; 1963.p.610.

[27]STANAG 4061 MET Adoption of a Standard Ballistic Meteorological Message (METBKQ).2000.

[28]Composite authors.Artillery meteorology,Department of the Army 1970,FM 6-15 C1,p.312.

[29]Composite authors.Tactics,techniques and procedures for field artillery meteorology,Department of the Army 2007,FM 3-09.15,p.270.

[30]Dickinson ER.The production of firing tables for cannon artillery.BRL report R 1371.Aberdeen proving ground,MA:RDT&E project 1T523 801A 287;1967. p.110.

[31]Longdon LW,et al.Textbook of ballistics and gunnery.Volume one and twovol.1987.London:Her Majesty’s Stationery Of fice;1984.p.806,521.

[32]Composite authors.Tactics,techniques and procedures for field artillery, manual cannon gunnery.Department of the Army;1996.p.757.FM 6-40.

[33]STANAG 4119 Adoption of a Standard Cannon Artillery Firing Table Format. 2007.

[34]Rosenwasser Je N,Jusupov RM.Sensitivity of control systems(in Russian). Moscow:Nauka;1981.p.464.p..

[35]Kato T.Perturbation theory for linear operators.Reprint of the 1980 edition. Berlin,Heidelberg:Springer-Verlag;1995.p.620.

[36]STANAG 4082 MET Adoption ofa Standard Artillery Computer Meteorological Message(METCMQ).

29 January 2017

*Corresponding author.Oprox,Inc.,Kulkova 8,Brno 615 00,Czech Republic.

E-mail addresses:cech-vladimir@volny.cz(V.Cech),jiri.jevicky@centrum.cz (J.Jevicky).

Peer review under responsibility of China Ordnance Society.

http://dx.doi.org/10.1016/j.dt.2017.04.001

2214-9147/©2017 The Authors.Published by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

Received in revised form 24 March 2017

Accepted 10 April 2017

Available online 12 April 2017