加速特性对磁悬浮转子瞬态响应的影响

杭州应用声学研究所 俞思源浙江工业大学光伏电力与微网研究中心 胡雄心浙江机电职业技术学院 尤光辉

加速特性对磁悬浮转子瞬态响应的影响

杭州应用声学研究所 俞思源
浙江工业大学光伏电力与微网研究中心 胡雄心浙江机电职业技术学院 尤光辉

通过建立径向磁悬浮轴承—Jeffcott转子动力学模型，为磁悬浮转子瞬态响应分析提供理论指导。并在SAMCEF ROTOR有限元分析软件中建立Jeffcott转子结构模型，定义转子不平衡条件及磁悬浮轴承支撑参数，分析转子在不同的加速度加速条件下的瞬态位移及模态变化规律。分析结果为电机加速方案的优化奠定基础。

磁轴承；模态分析；瞬态响应

0 前言

磁悬浮轴承具有一系列传统轴承所无法比拟的优点，尤其是在高速旋转机械中，比传统的滚动和滑动轴承更具优势。但是磁悬浮轴承转子无论在电机、飞轮储能等领域的应用中，都对其加速过程中的动态平衡和瞬态响应提出了高要求，良好的瞬态响应直接影响着磁悬浮转子运转的稳定性。目前国内外大多数的研究者研究了磁悬浮转子在工作转速以及匀加速过程中由于受到不平衡载荷的作用产生的瞬态响应，并且将研究重点集中在这一过程中不平衡载荷的变化所带来的影响。而忽略了飞轮转子在不同的加速度加速过程中的瞬态响应。为此本文通过建立磁悬浮轴承转子的数学模型及运用SAMCEF ROTOR有限元分析软件研究加速特性对磁悬浮轴承转子瞬态响应的影响。

1 磁悬浮轴承转子动力学建模[1]

磁悬浮轴承转子的应用领域一般都为超高速，转速都跨越了转子的一阶或二阶临界转速，成为柔性转子。因此，对刚性转子的动力学分析已经满足不了要求。为了更好地分析转子在超高转速下的瞬态响应，本文建立柔性转子模型进行分析。

Jeffcott转子是一种典型的极为简化的柔性转子，也称为Laval转子[2]，见图1。由于其结构特性，它非常适合用来模拟最基本的磁轴承柔性转子模型，从而研究转子的基本力学特性。

图1 Jeffcott转子模型

图2 弹性轴段模型

1.1 转子的运动方程的确立

在系统模态分析过程中，建立该系统的动力方程有助于从理论上研究其动力学特性。对于多自由度的运动而言，一般利用达朗贝尔定理、牛顿第二定律、哈密儿顿定理和Lagrange方程来建立系统的运动方程[3]。

公式()是一个N自由度线性系统运动微分方程，其中：[M]为系统的质量矩阵、[C]系统的阻尼矩阵、[K]为系统的刚度矩阵、{x(t)}为系统的广义坐标矢量、{F(t)}为作用在系统上的广义外力。

对所要研究的Jeffcott转子系统而言，可以将其划分为各自在结点处连接的三个部分：飞轮圆盘、转轴和支撑轴承。在转子系统运动方程的推到中，第一步需要建立飞轮圆盘、转轴和转子不平衡量的动能表达式，包括转轴的势能表达式。然后确立轴承的对转子作用力的虚功表达式。最后根据Lagrange方程得到系统的运动方程[4]。

1.2 刚性圆盘的运动微分方程[5]

在转子动力学中，通常用刚性飞轮圆盘的质量和转动惯量信息集中质量点来模拟整个圆盘。刚性飞轮圆盘的轴心节点的位移向量

用广义坐标来定义，得到其动能表达式。

其中md为刚性飞轮圆盘的质量。Jd和Jp分别为刚性飞轮圆盘的直径和极转动惯量。结合拉格朗日方程

原理得到：

其中qk为转子系统广义坐标，Qk为对应系统广义坐标qk的广义力。[Md]和Ω[J ]分别为飞轮刚性圆盘的质量矩阵和陀螺矩阵。

对应的广义力{Qd}有两种不同的情况，当圆盘处无支撑且忽略不平衡质量时，广义力包括圆盘的受到的来自转轴的作用力和力矩。当圆盘收到支撑约束时，还需将支撑处的束缚力和束缚力矩加入考虑。

1.3 弹性轴段的运动微分方程[4]

用铁木辛柯梁单元来表示转子转轴的小段轴段见图2。两端节点的位移向量可根据梁单元的广义坐标表示为：

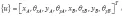
其中xA、yA分别为A截面在x和y方向的位移。θxA、θYA分别为A截面在X和Y方向的转角，xB、yB分别为B截面X和Y方向上的位移，θxB、θYB分别为B截面X和Y方向上的转角。弹性小段轴的长度为l，设定轴上随机截面与A截面之间的相互位移为s，该截面在X和Y的位移分别为为x和y，在X和Y方向的转角为θx和θy。

用形函数[N]单元两端节点位移向量来表示弹性轴小段任意截面的广义位移向量。

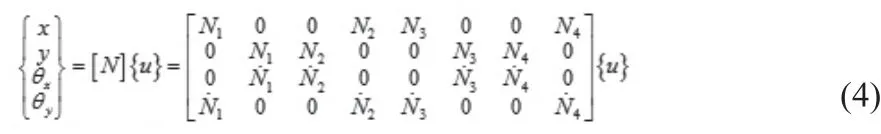
根据初始条件，得到形函数为：

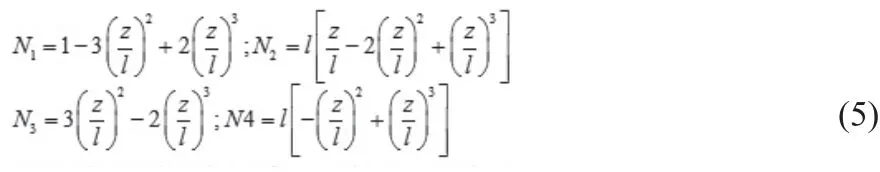
其中Z为截面在距轴段端部的距离，弹性小段轴的动能Ts和势能V 分别为：

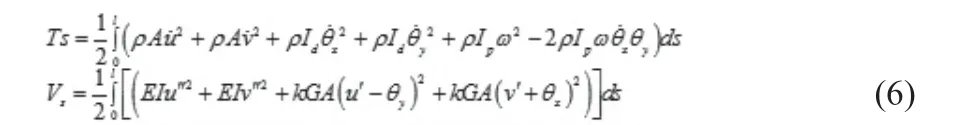
其中ρ为材料的密度，A为轴单元截面积，Id为轴段的直径惯性矩，Ip为极惯性矩。EI为材料的抗弯刚度。ω为材料切面剪切校正因子。G为材料剪切模量。

根据Lagrange方程，根据推导出转轴的运动微分方程：

其中{Qs}为转轴轴段广义力向量。[Ms]为移动和转动惯量一致的质量矩阵。Ω[Js]为回转矩阵。[Ks]为刚度矩阵。

因为弹性轴段的结构是轴对称的，所以其回转、质量和刚度矩阵可以表示为：分别为轴端单方向的移动惯性矩阵、转动惯性矩阵、回转矩阵和刚度矩阵。

其中

1.4 磁悬浮轴承的运动微分方程[4]

可以采用刚度阻尼单元来简化转子支承系统中的磁轴承，见图3。设定轴承的坐标是xb、yb。序号s( j )为其对应的轴颈中心结点。轴颈中心的坐标为xs( j )、ys( j )，则轴颈结点处受到的广义力为：为磁轴承的的阻尼矩阵和刚度矩阵。轴颈结点处的广义力实质上是由磁轴承产生的支承力。当为各向同性磁轴承时，kxy= kyx、cxy= cyx，则式变为：式中，

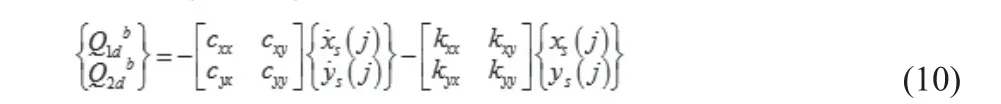
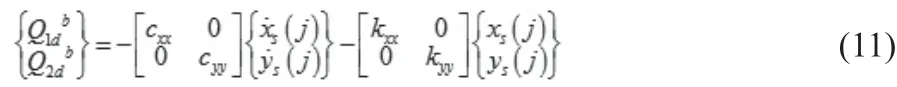
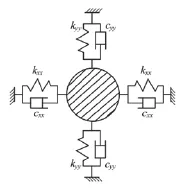
图3 简化的磁轴承单元模型

图4 SAMCEF中转子模型

1.5 磁悬浮轴承支撑的转子运动方程

通过前诉的分析得到了飞轮圆盘和转轴的质量、刚度和陀螺矩阵。同时转子受到的支承力为磁悬浮轴承作用在对应节点处的广义力。现在可以通过有限元法对磁轴承柔性转子系统的动力学响应进行求解。综合将各部分的质量、刚度和陀螺矩阵以及外力向量，则可得到磁悬浮轴承柔性转子系统的总体运动微分方程。

[M]为系统质量矩阵，Ω[J ]为系统回转矩阵，[K]为系统刚度矩阵。{Q}为转子所受的广义力，一般只包括轴承的支撑力和转子不平衡激励产生的广义力。通过求解总体微分方程则可以得到各节点的动力学响应。

2 有限元仿真分析

本文主要目的是分析转子在加速过程中，采用不同的加速度对转子瞬态响应的影响。由于磁悬浮转子受外界干扰较小，设定转子的不平衡载荷主要由转子本身的质量不均匀产生的质量偏心引起的，通过有限元仿真分析其瞬态响应[6][7]。

根据前面分析的Jeffcott转子，在SAMCEF里建立转子模型，如图4所示。

在固定的支撑条件下，首先求得飞轮转子前4阶临界转速，见表1。

表1 飞轮转子前4阶临界转速(r/min)

设定转子在加速过程中跨越前三阶临界转速，速度由0r/min到10000r/min。为了使研究结果更准确，所设定的加速度变化范围要足够大。根据要求设计加速时间分别为5秒、10秒和20秒，意味着加速度分别为120000r/min2、60000r/min2和30000r/min2。

为了使位移瞬态响应结果更清晰，记录转子位移变化最大的轴端及飞轮中心的位移瞬态响应变化，得到图5和图6中所示的位移瞬态变化图。

图5 转子轴端加速过程中位移瞬态响应

图6 转子中心加速过程中位移瞬态响应

从转子轴端和转子中心在不同加速度下加速过程中的位移瞬态响应来看，从总加速时间的12%左右时刻开始，转子轴端和中心都出现位移瞬态变化。根据时间和速度比例关系，在各加速过程中12%左右的时间点转子转速正好达到一阶临界转速。从图中还可以看出转子的最大瞬态位移发生在约65%的时间点，同样根据时间和速度比例关系，可以知道这个时间点转子转速正好在第三节临界转速附近。其余转速下位移瞬态响应比较平稳。

对比转子轴端和中心在不同加速度下位移响应的可以看出，随着加速度减小，转子轴端和中心处的位移变化幅度增大，在最大位移处变化最为明显。图7显示了不同加速度下，转子最大瞬态位移值以及相应的振型。

图7 不同加速度下转子最大位移响应与振型

从图7的可以看出，在5s、10s和20s加速时转子的最大位移分别为101.04mm、140.53mm和187.13mm。结合图3-14和3-15的位移瞬态响应图可以分析出，转子在加速过程中，不同的加速度所产生的瞬态位移响应也不一样。最大瞬态位移都会发生在弯曲临界转速附近。随着加速度的减小，瞬态位移会变大，在跨越临界转速时，特别是跨越弯曲临界转速时，瞬态位移的会变更大。

3 结束语

本文研究了磁悬浮轴承转子在加速过程中，不同加速度加速特性对其瞬态响应的影响。从理论模型和仿真结果可以得出：

(1)转子在加速过程中，最大瞬态位移发生在弯曲临界转速附近。

(2)不同的加速度加速特性下转子产生的瞬态位移响应不同。随着加速度的减小，瞬态位移会变大，在跨越临界转速时，特别是跨越弯曲临界转速时，瞬态位移的会变更大。

根据此结论，可以根据转子的临界转速结合电机加速特性，设计转子的加速方案，使转子具有更好的动态响应。其基本原则是在转子跨越弯曲临界转速时，充分提高加速度，来减小转子跨越弯曲临界转速时的最大位移和位移响应持续时间，从而降低振动损害风险，并且简化磁轴承的控制难度。在转子转速处于非临界转速阶段，可以减小加速度，从而减小电机功耗。此结论对磁悬浮轴承转子的加速动态性能设计具有重要的指导作用。

[1]谢振宇,徐龙祥,李迎等．磁悬浮轴承转子系统的稳定性及动态特性分析[J]．机械科学与技术,2004,23(7)．

[2]Seok-Myeong Jang,Un-Ho Lee．Design and analysis of thrust active[J]．magnetic bearing．JOURNAL OF APPLIED PHYSICS 103,07F122(2008)．

[3]王彦涛．分子泵磁轴承的模态辨识与试验研究[D]．黑龙江:哈尔滨工业大学,2009．

[4]杨志轶．飞轮电池储能关键技术研究[D]．安徽:合肥工业大学,2002．

[5]Lrich Schonhoff,Jihao Luo,Guoxin Li,etc．Implementation Result of u-synthesis Control for an Energy Storage Flywheel Test Rig[A]．Proceedings of the 7th International symposium on Magnetic Bearings．ETH zurich,Switzerland,August23-25,2000．

[6]张保强．磁轴承-转子系统的有限元模型修正及相关问题研究[M]．江苏:南京航空航天大学,2009．

[7]谢振宇,徐龙祥,李迎等．磁悬浮轴承转子系统动态特性的实验研究[J]．航空动力学报,2004,19(1),30-37．

The Effects of Acceleration Characteristic on The Transient Response of Magnetic Suspension Rotor

YU Si-yuan1,HU Xiong-xin2,YOU Guang-hui3（1.Hangzhou Applied Acoustics Research Institute，Hangzhou 310023，China；2.Photovoltaic Power and Micro-Grid Research Institute，Zhejiang
University of Technology，Hangzhou 310014,China；3.Zhejiang Institute of Mechanical & Electrical Engineering，Hangzhou 310053，China）

Establishing the rotor dynamics model of Jeffcott rotor as the theoretical guidance of transient response analysis of Magnetic Suspension Rotor.And making the structural model of Jeffcott Rotor by the finite element software named SAMCEF ROTOR.Then analyzing the transient displacement and modality variation regularity of the rotor under different acceleration conditions by def i ning the unbalanced condition and support parameters of magnetic bearing on the rotor.The analysis results lay a foundation for the acceleration program optimization of the motor.

magnetic bearing；modal analysis；transient response

俞思源（1988—），男，浙江杭州人，硕士研究生，主要从事水声行业机械结构等相关方面的研究。