优化模型在数学建模中的应用
杨依晨,柏 旭,李厚彪
(电子科技大学 数学科学学院,四川 成都 611731)
优化模型在数学建模中的应用
杨依晨,柏 旭,李厚彪
(电子科技大学 数学科学学院,四川 成都 611731)
在当今社会,数学建模因其应用的广泛性,受到人们越来越多的关注,而优化模型是其中最常用的模型之一。该文首先简要介绍了优化模型的3要素、一般建立步骤及分类;然后根据分类标准,整理了2000年至今的数学建模国赛中应用优化模型的题目;重点根据决策变量、目标函数的分类标准,分析了应用整数规划、动态规划及多目标规划的部分国赛题目,并给出了具体的优化模型范例。该文还介绍了最优化模型的解法,并总结了优化模型在数学建模中应用的重要性。
优化模型;数学建模;动态规划;整数规划;多目标规划
数学建模是联系数学与实际问题的桥梁,是数学在各个领域广泛应用的媒介,是数学科学技术转化的主要途径。数学建模在科学技术发展中的重要作用越来越受到数学界和工程界的普遍重视,已成为现代科技工作者必备的重要能力之一。数学建模的关键在于建立合理的数学模型,而建立数学模型的方法有很多,其中,最优化思想作为解决数学问题的重要思想之一,在解决实际问题中具有指导意义[1]。
1 优化模型
1.1 优化模型三要素及一般建立步骤
优化模型[2-4]是数学建模中最常用的模型之一。建立优化模型有以下3要素。
1)决策变量和参数
决策变量是由数学模型的解确定的未知数。参数表示系统的控制变量,有确定性的也有随机性的。
2)约束或限制条件
由于现实系统的客观物质条件限制,模型必须包括把决策变量限制在其可行值之内的约束条件,而这通常是用约束的数学函数形式来表示的。
3)目标函数
这是作为系统决策变量的一个数学函数来衡量系统的效率,即系统追求的目标。
建立优化模型处理实际问题的一般步骤是:1)将实际问题抽象成数学问题,收集有关数据和资料;2)建立优化问题的数学模型,确定变量,列出目标函数和约束条件;3)求解,一般通过编制程序,用计算机求最优解;4)最优解的检验和实施,将结果运用到实际中,得到该问题的优化解决方案。
1.2 优化模型分类
优化方法涉及的应用领域很广,问题种类与性质繁多,根据不同的原则可以给出不同的分类。按照有无约束条件可分为无约束最优化和有约束最优化;按照函数是否线性可分为线性规划和非线性规划;根据决策变量、目标函数的不同要求可分为整数规划、动态规划、网络规划、随机规划、几何规划以及多目标规划;根据问题的连续性可分为决策最优化和组合最优化,等等。
2 历年数学建模国赛中应用优化模型的题目
2000年至今的数学建模国赛中用到典型的最优化方法的题目[5]在表1中列出。根据1.2节的分类标准可对每个问题进行分类。例如,2008年的高等教育学费探讨问题,其中就用到了最优化方法中的多目标规划;2001和2007年的公交车优化调度问题不仅用到了最优化方法,也用到了图论的思想;2013年的碎纸片拼接问题用到了整数规划;2014年的嫦娥三号软着陆轨道确定和最优控制研究是一个典型的连续性最优化问题。

表1 历年数学建模国赛中应用优化模型的问题
3 优化模型在数学建模国赛中的应用分析
在实际问题的应用中,优化模型通常解决非线性规划与有约束条件的问题[6]。因此,本文主要根据决策变量、目标函数要求不同的分类方式,将优化问题分为建模中最常见的整数规划、动态规划及多目标规划3种形式进行举例分析。以2012年太阳能小屋问题、2013年碎纸片的拼接问题及2014年创意平板折叠桌问题的国赛题目为例,给出建立模型的全过程。
3.1 动态规划——创意平板折叠桌问题
动态规划是通过把原问题分解为相对简单的子问题来求解复杂问题的方法,主要适用于有重叠子问题和最优子结构性质的问题[7]。下面以数学建模国赛题(2014B)为例来说明动态规划的应用。
题目1:某公司生产一种可折叠的桌子,桌面呈圆形,桌腿随着铰链的活动可以平摊成一张平板。桌腿由若干根木条组成,分成两组,每组各用一根钢筋将木条连接,钢筋两端分别固定在桌腿各组最外侧的两根木条上,并且沿木条有空槽以保证滑动的自由度。试建立模型描述此折叠桌的动态变化过程。
分析:题目要求建立数学模型来描述此折叠桌的动态变化过程,也就是将折叠桌的变化过程分成若干步骤,再对每一步进行求解。为了分析折叠桌的动态变化过程,结合折叠桌的对称性,可将1/4的圆形桌面作为研究对象,考虑当折叠桌最外侧木条与地面夹角一定时内部各木条所在直线与地面的夹角大小。
解答:假设折叠桌面半径为R,第i根木条的长度为li(i=1,2,…,10),折叠桌最外侧木条与地面夹角为β,则当折叠桌成型立在地面时β达到最大值,有

式中:H为折叠桌面高度,单位为cm;h为长方形平板的高度,单位为cm;l10为折叠桌最外侧木条的长度,单位为cm。
当折叠桌最外侧木条与地面夹角为β时,设各木条与桌面连接处的顶点坐标为Pi(i=1,2,…,10),钢筋在各木条中的坐标为Qi(i=1,2,…,10),根据Pi和Qi,可得第i根木条所在直线的方向向量ei。
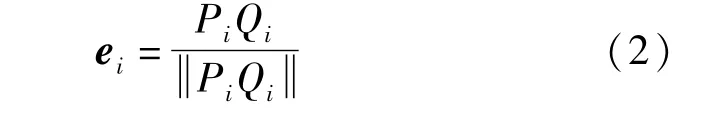
由式(2)得到第i根木条所在直线的方向向量ei,结合几何关系,第i根木条与地面的夹角βi等于ei与y轴方向向量的夹角,即

综合式(1)~式(3),可得当β一定时,第i根木条与地面的夹角:

通过木条与地面的夹角βi,可以得到此折叠桌在展开过程中的动态变化过程。
3.2 整数规划——碎纸片的拼接
将规划中的变量(全部或部分)限制为整数,称为整数规划。整数规划的一种特殊情形是0-1规划,它的变数仅限于0或1[8]。下面以2013年B题碎纸片的拼接为例说明0-1规划的应用。
题目2:对于给定的来自同一页印刷文字文件的碎纸机破碎纸片建立碎纸片拼接复原模型。
分析:对于碎纸片的拼接与复原问题,追求复原图与原图误差最小,因而拼接时应考虑任意两片碎纸片边缘相似度最大为拼接原则。自然,所建模型为优化模型。
解答:
1)目标
对碎纸片进行左右拼接时,以边缘相似度最大为目标,即:

式中,定义Cpq为任两张纸片p与q之间的边缘相似度,表示两碎纸片之间左右边缘0-1值相同的格点占总格点个数的百分比。将纸片的图像像素设为1 980×72,设纸片个数n=19,bijk为第k个纸片对应的0-1矩阵;矩阵bijk的行数l=1 980,列数为m=72,其中bijk=1表示白色,bijk=0表示黑色。

式中,1≤p≤19,1≤q≤19并且p≠q。
2)约束条件
每个碎纸片由左边进入拼接的时候,表示由碎纸片左边缘为入口来拼接,则有:

式(7)对所有q成立。
每个图只能从右边出去进行拼接,表示由碎纸片右边缘为出口进行拼接,则有
式(7)中,xpq为0-1变量,(1-bilq)≠0表示左边缘不是全为白色,即碎纸片不在最左边的,它的左边仍存在纸片与其相连,反之则该碎纸片为最左端,不存在纸片位于其左端;式(8)中,(1-bi72p)≠0表示右边缘不是全白色,即碎纸片的位置不在最右端。它的右边仍有纸片与其相连,反之右边没有纸片与其相连。此外,还需
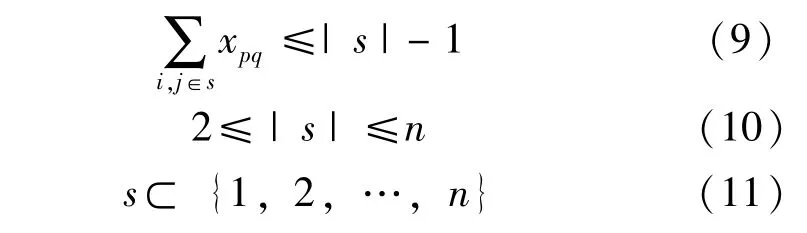
式(9)~式(11)表示碎纸片拼接时除最左端和最右端外,各碎纸片不构成圈。
综上所述,将图像复原的问题类比转化为图论问题,建立优化模型为:目标函数为式(5);约束条件为式(8)~式(11)。
3.3 多目标规划——太阳能小屋
多目标规划主要用于解决多于一个目标在给定区域上的最优化问题[9]。
题目3:对于太阳能小屋设计问题建立优化模型,解决贴附、架空两种安装方式下,小屋外表面光伏电池阵列最优铺设的问题。
分析:该问题是典型的优化问题,要求解决在房屋表面太阳能的最优铺设与设计问题。考虑贴附铺设方案关键在于选定光伏电池组件、逆变器及确定铺设方式,而结合房屋各个立面的尺寸的铺设(避开窗户和门)限制了光伏电池组和逆变器的选择。光伏组件的电压和功率限制了逆变器的选择。基于上述条件限制,可以考虑将房屋立面切割为矩形块,并在矩形块中放置光伏组件与逆变器捆绑成的电池组件分组阵列(矩形)。下面给出双目标规划模型进行参考。
解答:
1)目标
全年太阳能光伏电池转化的交流电总电量最多;单位发电量的成本费用最少,即

式中:E为交流总电量,单位为J;Q为太阳光照一年总辐射强度,单位为W/m2;P为总成本,单位为元。

2)约束条件
A.房屋墙面(或屋顶面)长度的约束,即所有横铺的矩形的长与竖铺的矩形的宽之和需小于墙面的长度,即

B.房屋墙面(或屋顶面)宽度的约束,即所有横铺的矩形的宽与竖铺的矩形的长之和需小于墙面的宽度,即
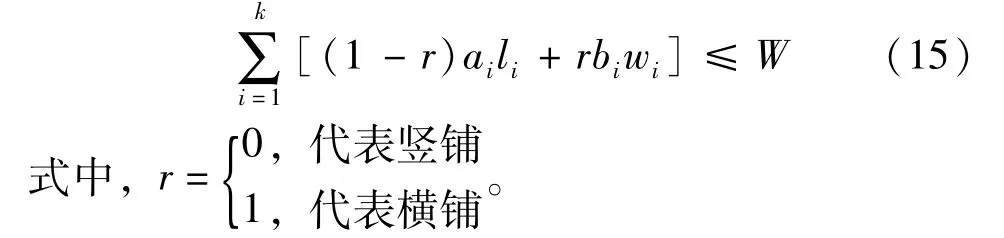
C.第i种矩形竖放个数不超过总数,即

D.第i种矩形竖放个数不超过总数,即

E.第i类矩阵中型号为j的电池的约束
首先约定矩阵中电池、逆变器只能横铺放置,且一个矩形中只能放置一个逆变器电池组件长度的最大值+逆变器长度=矩形的长,即:

F.电池组件宽度与逆变器宽度的最大值等于矩形的宽,即:
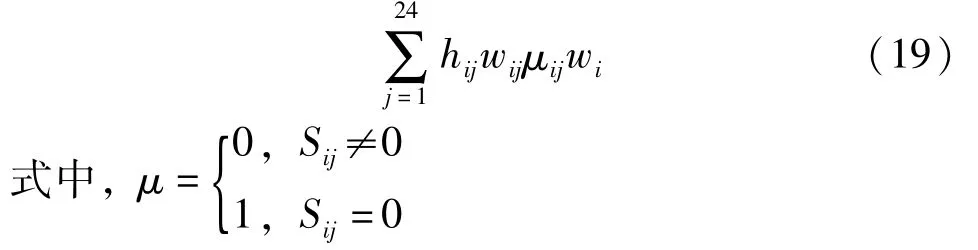
G.电压要求
由题目要求,多个光伏组件串联后可以再进行并联,并联的光伏组件端电压相差不应超过10,可以得到

H.功率要求
由题目要求,逆变器的选配容量应不小于光伏电池组件分组安装的容量,可以得到
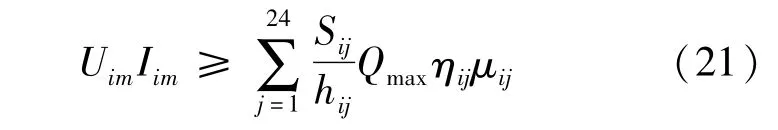
最终的优化模型:目标函数为式(12);约束条件为式(14)~式(21)。
4 解法简介
在求解最优化问题时,最常用的方法是单纯形法和对偶理论。而在实际中常见的是非线性规划问题,其求解的总体思想是进行局部线性化使问题简化,可以用最速下降法、共轭方向法、牛顿法或拟牛顿法等方法求解。目前,非线性规划问题还没有一个统一的解法,在数学建模的求解中,也是对某一类问题给出特定的算法,如遗传算法、模拟退火算法、蚁群算法等。这些算法可以通过MAT LAB[10]、LINGO[11]、Mathematic等相应专业软件来实现。
5 结束语
优化方法的应用非常广泛,主要有以下7个方面:1)微分学中求极限;2)无约束最优化问题;3)常用微分公式;4)凸集与凸函数;5)等式约束最优化问题;6)不等式约束最优化问题;7)变分学中求极限。在求解这些数学问题时,我们会大量地用到最优化模型,而在解决实际问题时,我们也常会用到最优化理论。
[1]姜启源,谢金星,叶俊.数学建模[M].4版.北京:高等教育出版社,2011.
[2]陈宝林.最优化理论与算法[M].北京:清华大学出版社,2005.
[3]郭科,陈聆,魏友华.最优化方法及其应用[M].北京:高等教育出版社,2007.
[4]高晓梦,贺祖国.最优化方法与数学建模[EB/OL].北京:中国科技论文在线[2010-01-26].http://www.paper.edu.cn/releasepaper/content/201001-1097.
[5]刘来福,曾文艺.数学模型与数学建模[M].3版.北京:北京师范大学出版社,2003
[6]胡运红.非线性最优化问题及其算法研究[J].运城学院学报,2003,21(3):9-10.
[7]胡运权.运筹学基础及应用[M].6版.武汉:武汉大学出版社,2014.
[8]VASERSTEIN L N,BYRNE C C.线性规划导论[M].谢金星,姜启源,张立平,译.北京:机械工业出版社,2006.
[9]傅家良.运筹学方法与模型[M].上海:复旦大学出版社,2014.
[10]董文永.最优化技术与数学建模[M].北京:清华大学出版社,2010.
[11]卓金武.MATLAB在数学建模中的应用[M].北京:北京航空航天大学出版社,2014.
[12]谢金星.优化建模与LINDO/LINGO软件[M].北京:清华大学出版社,2005.
The App lication of Optim ization M odel in M athematical M odeling
YANG Yichen,BAIXu,LIHoubiao
(School of Mathematics Sciences,University of Electronic Science and Technology of China,Chengdu 611731,China)
Mathematicalmodeling is gainingmore and more attention because of its extensive application.The optimizationmodel is one of themost commonly used models.Firstly,this paper introduces the three elements of the optimization model,the general es tablishment of steps and classifications.Then,according to the classification criteria,this paper lists several subjects using the optimi zation model from Contemporary Undergraduate Mathematical Contest in Modeling since 2000.According to the classification standard of decision variables and objective functions,the subject of application of integer programming,dynamic programming and multi-objec tive programming are analyzed and a specific example of them is given.At the same time,the solution of the optimizationmodel is sim ply introduced.Finally,we summarized up the application of optimization model in mathematicalmodeling.
optimization model;mathematical modeling;dynamic programming;integer programming;multi-objective pro gramming
O151.2
A
10.3969/j.issn.1672-4550.2017.03.006
2015-11-25;修改日期:2017-04-15
电子科技大学教学研究(Y03003023901002010)。
杨依晨(1995-),女,本科,学生,主要从事数学建模和应用数学方面的研究。
李厚彪(1976-),副教授,lihoubiao0189@163.com

